基于三维流函数的无线传感器网络移动Sink避障机制研究∗

张美燕蔡文郁严求真

(1.浙江水利水电学院电气工程学院，浙江 杭州310018；2.杭州电子科技大学电子信息学院，浙江 杭州310018)

基于移动Sink节点的数据采集方式逐渐成为无线传感器网络的一个重要研究方向[1－2]。随着自动化和智能化程度的不断提高，无人小车、无人机、水下航行器等智能机器人系统逐渐应用于各种传感器网络中[3－4]。在Sink节点进行移动数据采集过程中，计算的优化路径必须能够规避无线传感器网络中可能存在的各种类障碍物。传统的自主机器人避障是通过雷达、声呐、激光等传感器感知周围的环境信息，确定当前环境的障碍物分布，并根据各种传感器采集到的感知数据进行有效路径避障。因此，避障路径规划已经成为移动机器人领域的重要研究课题，也是无线传感器网络中Sink节点移动数据采集领域的一个技术难点。

目前关于无线传感器网络中移动Sink节点路径规划的研究较多，但是考虑障碍物躲避特性的优化路径规划研究相对较少[5]。1986年，Khatib提出了经典的人工势场法(Artificial Potential Fields，APF)[6]，虽然人工势场避障算法非常简单，但是缺陷在于目标点对移动物体产生的引力与障碍物对移动物体产生的斥力相混合，局部极值点导致避障失效。后续研究也对人工势场避障方法进行了改进，Volpe等人提出基于超二次型(Super Quadric)的人工势场结构[7]代替传统二次型势场，并对势场函数加以修正。流函数法[8]作为一种新型的避障方法，借鉴流体力学的概念建立了势场区域，通过模拟水流运动机理，规划出的航线能够像流水避开岩石一样平滑绕过障碍物，还能避免局部最小问题。文献[9]中引入流函数以解决障碍环境下单机器人的导航控制，从而产生光滑的无碰路径，避免与障碍物发生碰撞。文献[10]通过对单个障碍物流函数进行加权求和，解决了两个障碍物重叠情况下的路径规划问题。文献[11]针对水下机器人在实际应用中由于自身机动性、探测性能约束而产生的问题，改进了传统的流函数法，结果验证了改进算法能够有效地规划路径。文献[12]研究了流函数法在无人机航线规划中的应用，将地形障碍和雷达等威胁等效为圆柱体，推导了流体运动的复势函数，将其应用到多障碍物环境中。文献[13]利用流函数解决单个移动Sink节点的避障问题，提出了采用虚拟Leader和二叉树结构的多移动Sink节点Swarming控制模型。文献[14]提出改进的流函数规划无人机在复杂地形环境的航线。针对传统流函数法面对多个障碍物时存在的问题，提出了一种基于虚拟动态目标的方法，解决了两个障碍物重叠情况的航线规划问题。图1所示为单个和多个障碍物情况下的平面流场分布情况，可以发现移动Sink节点沿着流线方向运动能够实现避障效果。

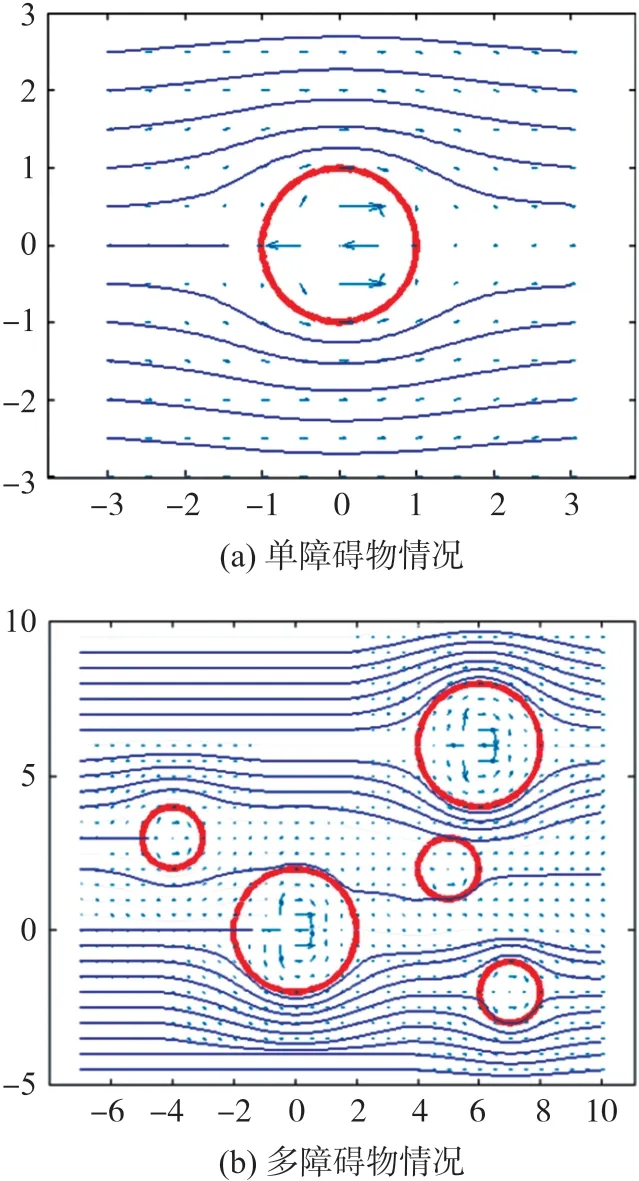
图1 平面障碍物场景下流场分布

综上所述，目前一些研究已将流函数方法应用于无人机或无人航行器的避障路径规划领域，但是基本上都是针对二维平面应用环境，缺乏三维环境下基于三维流函数的避障路径研究。本文将流函数应用到三维无线传感器网络环境中，利用球型障碍物在Z轴分层的方法实现三维流场计算，并且提出椭圆形路径变形方法克服“滞点”问题，从而求取移动Sink节点在三维无线传感器网络中的避障优化路径。

1 算法描述

无线传感器网络中分布的实际障碍物一般是不规则的，但是由于水流、风冲刷、腐蚀等影响，长时间作用下的障碍物一般都呈现了凸型多边体形态[15]。为了简单起见，本文以障碍物的质心位置为球心、安全半径为R的规则球体来表示需要躲避的障碍物范围。

基于凸球型障碍物的避障路径规划模型如图2所示:在三维传感器网络空间内随机分布若干个球型障碍物，移动Sink节点沿着预先设定的路径进行移动数据采集。避障规划的目标是使移动Sink节点所规划路径中的任何一点都不触碰到障碍物范围，而且规划路径要尽量保持连续和平滑。基于以上优化模型，本文借鉴流函数的思想并进行三维扩展，设计了适合三维传感器网络空间的有效避障路径规划方法。本文假设移动Sink节点在移动之前就已获取了全局网络空间内障碍物的分布情况，因此可根据障碍物分布计算整个区域的三维流场分布。

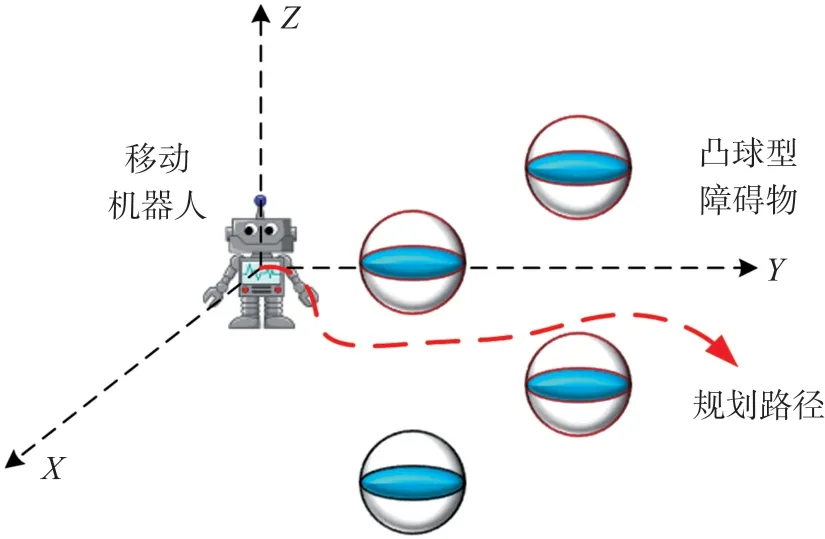
图2 基于球型障碍物的避障路径规划

流体力学中流体的绕流运动理想情况下可以看成是无旋运动，如果理想流体在某一源点是无旋流，则该流体在源点周围也是无旋流[16]。对于任意的标量函数ϕ，存在∇×∇ϕ＝0，所以满足无旋性的条件可以定义为:uf＝∇ϕ，其中uf为速度势，该无旋流定义为势流场[17]。速度势uf可表达为uf＝u＋iv，i指实数的虚部，因此有以下公式:

在直角坐标系中，在二维不可压缩流动场中需要满足质量守恒方程:因此可引入一个新的函数定义如下[17]:

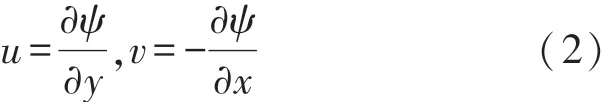
如果满足上述条件，则上述函数被称为流函数，流函数是表示流线的函数[18]。令球心位置为(Ox，Oy)，球体半径为R，则在统一流场(洋流强度为U)作用下的流函数公式可以推导得到[18]:

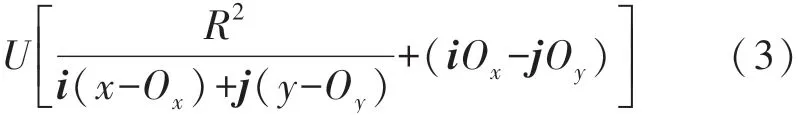
由上述的推导过程可知，使用流函数的概念进行避障路径规划，实质上是将移动Sink假设为水流体的一部分，利用虚拟的流线作为移动Sink的运动轨迹。因此，可以按照上述的势函数和流函数公式生成避障流线分布，让移动Sink节点根据起点位置选择相应的流线，并沿着该流线运动，就可以避开相应的障碍物。基于流函数的路径规划可以满足躲避障碍物的需求，同时还可以保持运动路径的连续性和平滑性。

下文主要推导三维流函数的存在条件和构造方法。在不可压缩的无旋场中，由于球体障碍物是立体对称的，因此三维流函数可以通过将X－Y平面经过Z轴扩展到X－Y－Z三维坐标系。三维空间球型障碍物环境下的流场计算方式如图3所示:本文将球型障碍物用不同的Z值平面去切割，切割成一个个不同半径R∗的圆形障碍物，因此可以求出对应不同Z坐标的圆形障碍物的流函数分布，如图4所示。按照不同Z坐标下的流场曲线，移动Sink根据自身的起点位置选择合适流线进行避障路径规划。

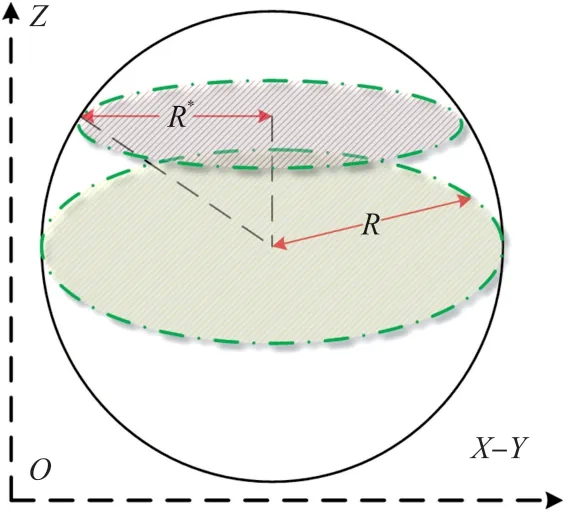
图3 三维空间球型障碍物环境下流场计算模型

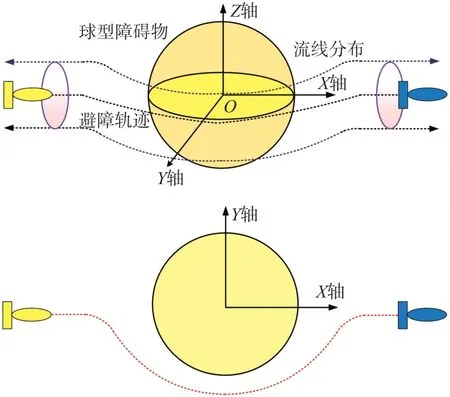
图4 基于三维流函数的球型障碍物避障方法

为了克服传统流函数避障曲线存在的“滞点”问题[10]，本文提出了一种新型的椭圆形路径变形方法。当根据起始位置所选择的流线刚好处于“滞点”位置时，将圆形轨迹调整为椭圆形路径，从而克服无法求解避障路径的问题。

椭圆形路径变形算法如图5所示，圆形障碍物的半径为r，令其等于椭圆形的宽b＝r，椭圆长a设为a＝2r，即在距离障碍物球形等于两倍障碍物半径时就启动椭圆路径变形算法。为了控制方便，将规划路径离散化成[(x0，y0)，(x1，y1)，…，(xn，yn)]，然后进行各个计算路径点的速度偏移。路径点(x0，y0)到路径点(x1，y1)的连线与X轴正向的夹角θ可以计算如下:

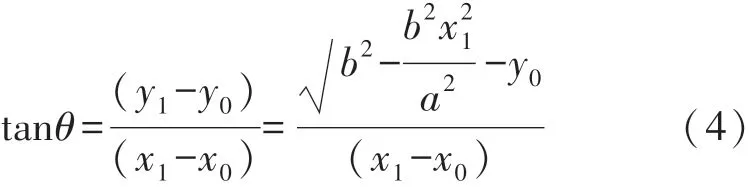
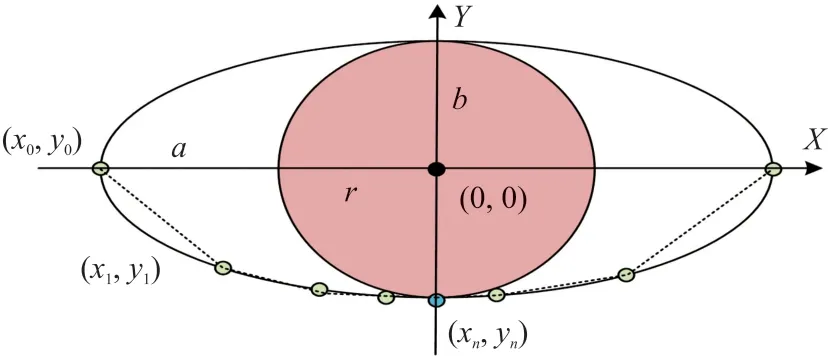
图5 椭圆路径变形方法

假设沿X正轴的洋流强度为U，移动Sink节点在Y负轴方向的速度分量为V0，因此在路径点(x0，y0)只要满足式(4)所示的速度条件，就可以沿着曲线行进到路径点(x1，y1)，从而避免流函数的“滞点”问题。

椭圆路径变形算法的仿真结果如图6所示:

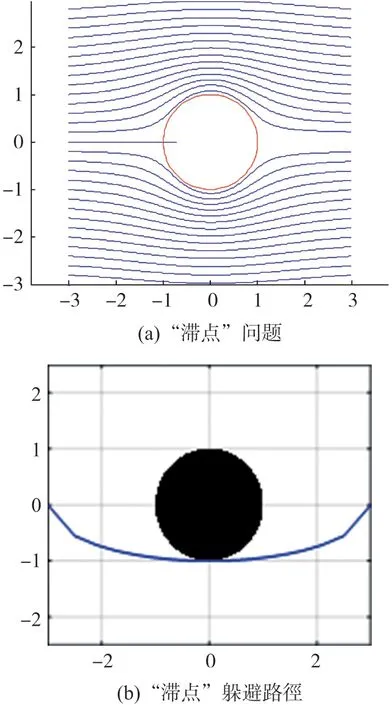
图6 椭圆路径变形方法仿真结果

2 仿真结果

基于流函数的三维避障算法采用MATLAB软件进行仿真，采用的方法如上文所述。仿真场景设置如下:三维无线传感器网络场景中分布多个不同半径的球型障碍物，随机选择移动Sink节点的起点位置计算整体空间的虚拟流场。本文的主要仿真参数选取如表1所示，单位均为基本单位(Unit)。

表1 仿真参数

二维平面流函数的分布情况如图7所示。随机分布如表2所示的多个障碍物时，利用流函数获得的避障路径如图8所示，虚线加粗的流线为根据起点位置所确定的移动Sink节点的运动路径轨迹。立体空间内不同Z轴位置的流线分布如图9所示，可见不同Z轴对应的障碍物在X－Y平面投影不一样，利用本文提出的Z轴分层方法就可以获取不同Z坐标时的流线分布，从而获取三维环境下的全局流线分布，移动Sink节点可以根据目前自身所处的Z坐标选择合适的流线路径进行移动。

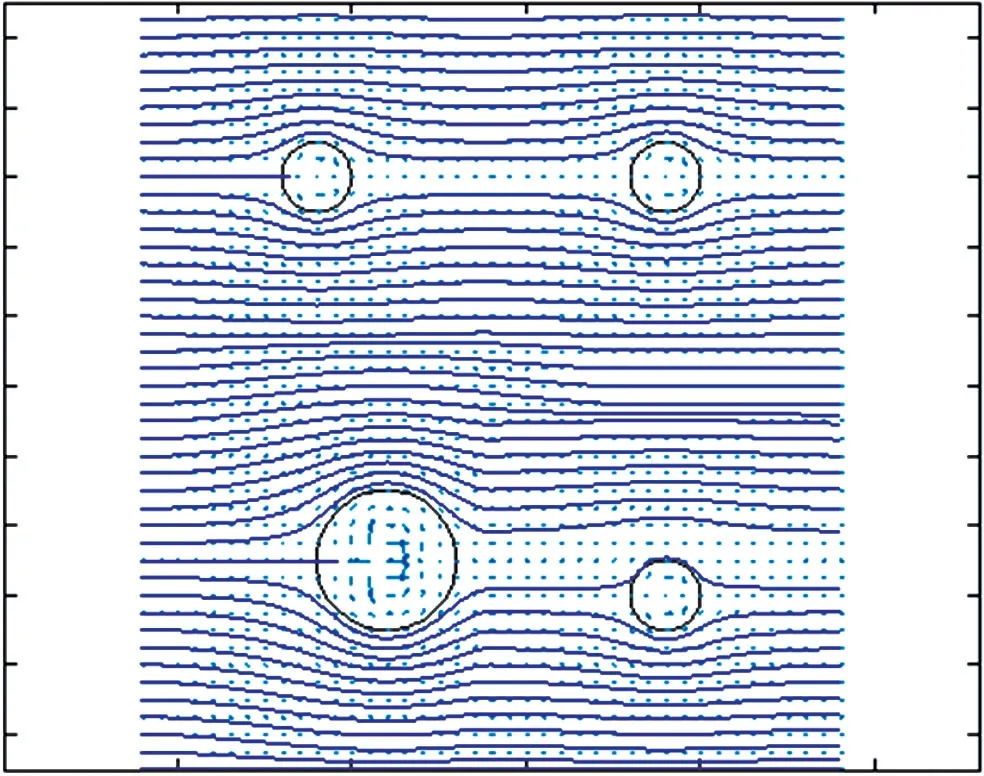
图7 平面流线仿真结果

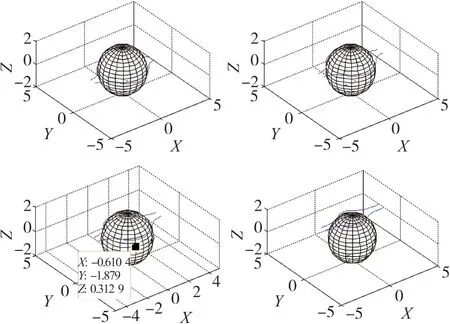
图9 三维空间内不同Z位置的流线分布

表2 多障碍物位置分布

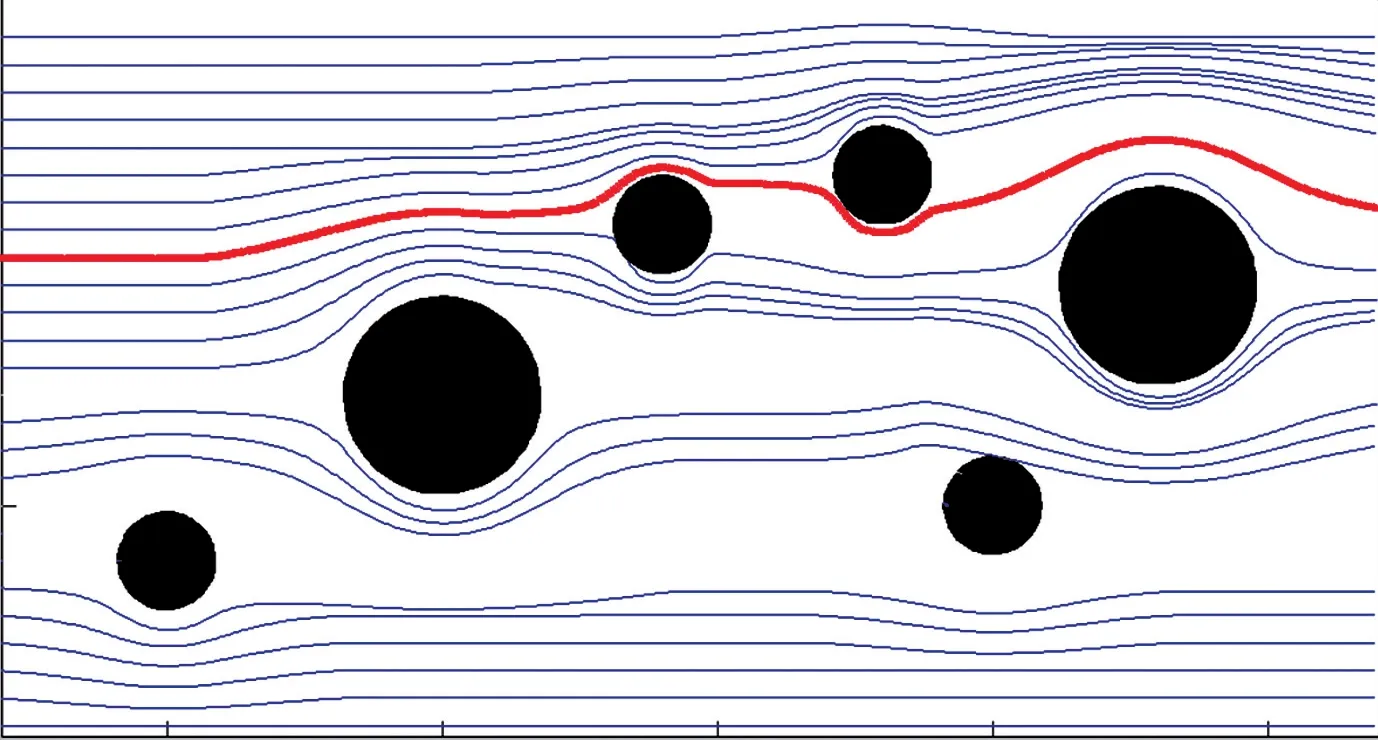
图8 多障碍物平面避障路径

下文从三维扩展角度分析本文提出的三维流函数避障算法的性能。

三维传感器网络中存在单个球体障碍物情况下，移动Sink节点的起点位置不同，得到的流函数避障路径如图10所示，根据流线分布获取三维空间不同起点到终点的避障轨迹，从而验证了本文提出的三维流函数避障方法能够有效躲避单个障碍物。

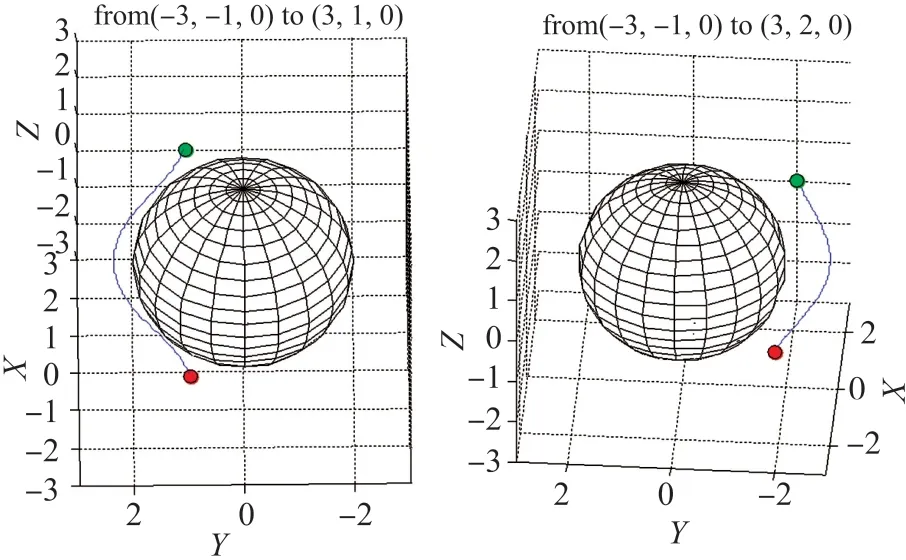
图10 单障碍物三维避障路径

当三维传感器网络内存在随机2个球型障碍物情况下，移动Sink节点的起点位置相同，获得的流函数避障路径如图11所示。为了表现清晰，图11展现了多障碍物情况下三维避障路径的俯视图。根据流线分布获取三维空间不同起点到终点的连续避障轨迹，从而验证本文提出的三维流函数避障方法能有效躲避多个障碍物。

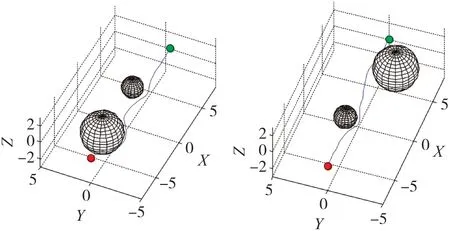
图11 两障碍物Sink节点三维避障路径

在较大区域的三维传感器网络中随机分布10个半径不一的球型障碍物时，基于流函数避障的移动Sink节点轨迹如图12所示。从仿真结果可以发现，利用本文所提出的流函数避障方法，在障碍物较为密集的三维无线传感器网络可以搜索到优化的避障路径。从获取的实际轨迹中也可以发现，利用流函数避障方法获取的移动Sink轨迹具有良好的连续性和平滑性。

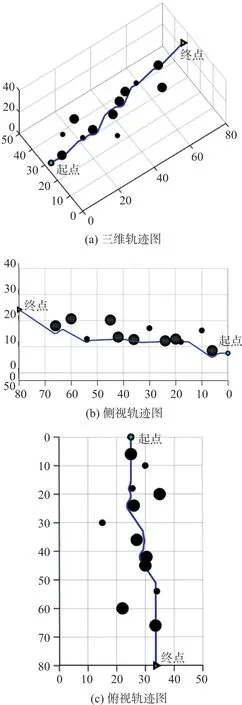
图12 多障碍物Sink节点三维避障路径轨迹图

3 结语

为了保证移动Sink节点在三维无线传感器网络中路径能够有效躲避多个随机分布的障碍物，本文提出一种利用三维流函数为移动Sink节点选择优化避障路径的方法。仿真结果表明，通过三维流函数所规划出的避障路径具有良好的连续性、平滑度和和高效的避障率，可以满足移动Sink节点在移动运动中躲避障碍物的需求。后期的研究将集中于构建更多种形状障碍物情况下的三维流函数分布，同时分析比较均匀流函数和汇流函数的避障效果。