基于自适应增量集成学习的非平稳金融时间序列预测
2021-10-27于慧慧
于慧慧,戴 群
(南京航空航天大学计算机科学与技术学院/人工智能学院,南京211106)
引 言
金融市场在现代社会的经济发展中起着非常重要的作用。在过去的几十年中,对金融市场动向的分析已在金融、工程和数学等领域得到了广泛的研究,这些研究可以分为基础分析和技术分析两类。基础分析研究了影响市场走势的所有经济因素,它对于支持长期决策非常有用。技术分析认为,价格已经包含了影响市场走势的所有基本面,它通常将历史价格和一些技术指标建模为历史时间序列,并认为历史环境总会重演。
时间序列是在固定采样间隔内收集到的一系列观测结果[1]。现实世界中的许多动态过程都可以建模为时间序列,例如股票价格变动[2]、城市天气[3]、黑子数和疾病发生率等。如果要预测这些过程来帮助生产、生活,则需要了解时间序列预测(Time series prediction,TSP)。TSP是指基于历史时间序列生成模型来预测未来趋势的过程。与金融产品相关的时间序列称为金融时间序列(Financial time series,FTS),诸多因素的影响导致其极为复杂。从20世纪80年代研究者将机器学习(Machine learning,ML)应用于金融市场开始,ML在金融市场预测方面取得了诸多进展,研究者也逐渐认识到现实生活中的FTS大多为非平稳金融时间序列(Non-stationary FTS,NS-FTS)。但是,ML在NS-FTS上的应用仍有诸多挑战,主要包括:(1)NS-FTS被认为是确定性混沌的时间序列。它对初始条件敏感,因此利用历史数据对其进行长期预测是不现实的。(2)NS-FTS具有非线性、非平稳性的特征,这导致其数据分布会随着时间发生改变,如何跟踪变化并及时反应变化是一个难题。(3)NS-FTS具有高噪声的特征,这意味着无论建立何种模型,都无法获得序列的完整信息,需要消除噪声的影响;(4)一些NS-FTS具有周期性特征,如何在历史环境重现时准确快速地做出反应,是值得思考的问题。
现有的非平稳金融时间序列预测(Non-stationary FTSP,NS-FTSP)方法大致可以分为3类:(1)传统的统计学方法。它是最早应用于NS-FTS的一类方法,其中的代表方法有差分整合滑动平均自回归(Auto-regressive integrated moving average,ARIMA)模型[4]和广义自回归条件异方差(Generalized auto-regressive conditional heteroscedasticity,GARCH)模 型[5]。ARIMA模 型 曾 被 广 泛 地 应 用 于NS-FTSP任务,但是由于它需要通过差分过程对NS-FTS进行平稳化处理,所以必然会影响模型的预测精度和效率。GARCH模型是一种使用过去变化和方差来预测将来变化的方法,它可以很好地拟合具有波动特征的序列。但是同ARIMA一样,它也需要对NS-FTS进行平稳化处理。可见传统统计学各种方法由于自身线性结构的约束,在实际应用中并不能达到很好的效果。(2)计算智能方法。此类方法有很多,其中的代表方法有人工神经网络(Artificial neural network,ANN)[6]、模糊逻辑(Fuzzy logic,FL)[7]和支持向量机(Support vector machine,SVM)[8]。ANN作为非线性预测模型具有良好的自学能力、函数逼近能力,在NS-FTSP领域得到了广泛的应用。但是ANN往往需要大量的训练数据,网络结构和网络参数难以确定,收敛速度慢,容易陷入局部最优。FL通过产生模糊的NS-FTS,模拟人类思维得出不确定的知识,然后将其变换为精确的预测值来完成预测任务。但如何生成合适的模糊规则是一大局限。SVM结构简单、泛化能力强,在NS-FTSP领域上得到了较好的应用,但只适用于小样本学习。(3)混合预测方法。实验表明,单一模型很难全面反映预测对象的整体变化规律,特别是在NS-FTSP这种具有高度不确定特征的任务上,所以混合预测方法应运而生,并成为现阶段最流行的方法。混合预测方法通过组合多种方法,包括上述提到的传统统计学方法和计算智能方法,来得到综合信息,从而提高最终模型的预测性能和稳定性。
实现混合预测方法的方式有两种:一是通过增量学习(IL)[9]和集成学习(Ensemble learning,EL)[10],比如文献[11-12];二是通过分阶段思想来实现,比如文献[13-14],基本思想是先将NS-FTS进行分解,然后分别用模型进行预测,最后再将预测结果组合起来。IL指一个模型在保存大部分旧知识的同时,不断从新数据中学习新知识的过程。应用于非平稳环境中的IL算法需要满足以下条件[15-16]:(1)任何训练数据集仅被学习一次,所学知识将以增量方式存储在模型参数中;(2)因为最新的数据集可以最好地表示当前环境,所以应根据知识与当前环境之间的关系对知识进行分类并动态更新;(3)模型应具有协调旧知识与新知识之间冲突的策略,即应有一种机制来监视模型在新旧数据上的性能;(4)模型应及时遗忘无关的知识,但在历史环境发生重现时,又能重新回忆起这些知识。EL指构建并结合多个基模型来完成学习任务的过程,它有3个要素:数据采样、训练基模型和组合基模型。至今EL已广泛应用于各种机器学习任务,比如特征选择、置信度估计、不平衡数据分类、以及非平稳环境学习等方面。主流的EL方法有以随机森林[17]为代表的装袋(Bagging)方法[18]和以AdaBoost[19]为代表的提升(Boosting)方法[20]两大类。Bagging是一种基于自助采样法并行生成不存在强依赖关系的基模型的方法。Boosting是一种串行生成存在强依赖关系的基模型的方法。AdaBoost作为Boosting的代表算法,其主要思想是:每次通过最新的数据分布迭代地训练一个基模型,再根据该基模型的性能调整样本分布,减少擅长数据的权重,增加不擅长数据的权重,以使先前不擅长的数据在后续训练过程中得到更多的关注。最后减少误差大的基模型的权重,增加误差小的基模型的权重,并将其加权组合起来。通过文献[21]知道,应用于非平稳环境学习的EL方法有3个思路:(1)更改组合规则以使已存在的基模型适应非平稳环境,例如加权多数投票算法[22];(2)利用新数据集在线更新模型,如在线提升算法[23];(3)添加新的基模型或利用新基模型替换集合中贡献最小或年龄最小的成员[24]。
结合以上背景,本文提出了一种自适应增量集成学习(Self-adaptive incremental ensemble learning,SIEL)算法,用于解决NS-FTSP问题。其思想是为每个NS-FTS子集增量地训练一个基模型,然后使用自适应加权规则将所有基模型组合起来。SIEL算法的具体步骤如下:(1)初始化数据分布,此时所有数据的权重是相同的。(2)计算当前集成模型在最新数据集上的相对误差,并根据该误差更新数据权重。(3)在最新数据集上训练一个基模型,将其作为新的集成成员以增量地构建基模型集合。(4)评估所有基模型在最新数据集上的性能,并对那些表现较差的基模型进行处理。值得注意的是,对于每个基模型来说,由于其生成时间不同,获得的性能评估数量也不同。(5)计算所有基模型的加权平均误差以自适应地更新基模型权重并消除噪声对基模型的影响。每个基模型在越新数据集下的性能具有越大的权重(因为越新的数据集越能表示下一个新环境,尤其是在NS-FTS中)。(6)使用加权规则组合每个基模型。此外,考虑到极限学习机(Extreme learning machine,ELM)[25]作为特殊的神经网络模型具有较高的可扩展性和较低的计算复杂度,但其隐含层参数的随机性又会影响集成模型的稳定性和鲁棒性。所以,本文选择它的改进算法核极限学习机(Extreme learning machine with kernels,ELMK)[26]作为SIEL算法的基模型。
SIEL算法的主要创新和贡献如下:(1)提出了一种新规则来自适应地更新数据权重。与AdaBoost在提升阶段中基于单个基模型更新数据权重的过程不同,SIEL算法基于当前集成模型的性能来更新数据权重,且更新后的数据权重不用于采样,而是用于评估误差。该规则有助于提高最终模型的泛化性和鲁棒性。此外,该规则为预测误差较小的数据赋予了较高的权重,从而加重了对此类数据表现不佳的模型的惩罚。(2)提出了一种新规则来自适应地构建基模型。与AdaBoost在提升阶段中基于总体数据训练基模型的过程不同,SEIL算法根据数据块训练基模型,提高了基模型的多样性。(3)提出了一种新规则来自适应地组合基模型。与AdaBoost在集成阶段中单纯地根据基模型误差决定基模型权重的过程不同,该规则可以使表现较差的基模型的权重变小甚至为零,从而达到暂时遗忘无关知识的目的。但当历史训练环境重演时,该基模型又会被分配较高的权重从而使忘掉的知识重新被记起,提高了算法的稳定性。并且SIEL算法基于时间对基模型误差进行了加权,为基模型在越新环境中的性能分配越高的权重,从而能有效应对下一个新环境。这使SIEL算法在保持稳定性的同时,提高了本身的可塑性。(4)为解决NS-FTSP问题提供了一个通用的框架,并取得了优异的性能。
1 算法描述
1.1 ELM算法
ELM是由黄光斌等提出的一种特定的单隐藏层前馈网络(Single-hidden layer feedforward networks,SLFNs)模型。与传统的SLFNs相比,其不同之处在于:(1)输入层与隐藏层之间的连接权重,以及隐藏层的偏置可以随机产生,也可以手动设置;(2)隐藏层和输出层之间的连接权重不需要通过迭代来反复调整,而是直接通过最小二乘法求解方程来确定。因此,在大部分情况下,ELM能在更短的时间内获得更优的泛化性能,且避免了局部最优问题。ELM算法结构如图1所示。
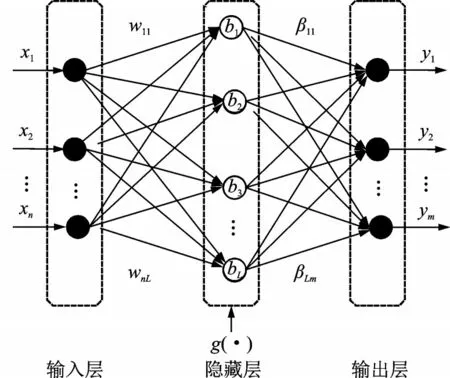
图1 ELM算法的结构图Fig.1 Block diagram of ELM algorithm
假 设 有N个 训 练 样 本(xi,ti),i=1,2,…,N,其 中xi∈Rd,ti∈Rm。若设置隐藏层节点数为L,那么ELM可以被表示为

式中:yi代表第i个样本的期望值,wj代表输入层和第j个隐藏层节点之间的连接权重,βj代表第j个隐藏层节点和输出层之间的连接权重,g(⋅)和bj分别代表隐藏层的激活函数以及第j个隐藏层节点的偏置。
那么对于这N个样本,可以得到

式中隐藏层输出矩阵为
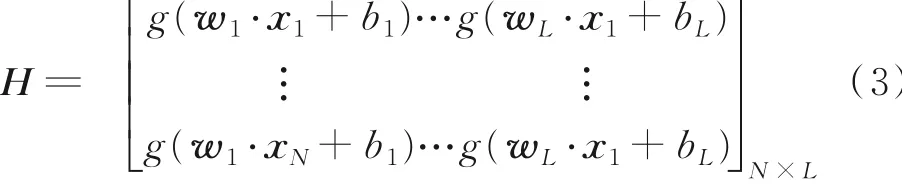
理想情况下的ELM应满足

根据相关知识,可以得到

式中H+代表H的广义逆矩阵。
1.2 ELMK算法
作为ELM的改进算法,ELMK使用核映射代替了ELM的随机特征映射,在保证泛化性能的同时,避免了随机性,加强了鲁棒性。ELMK在多分类、图像分类和回归预测等方面都有着广泛的应用。
ELMK定义如下

式中φ(⋅)代表未知的特征映射,能将原空间样本映射为另一个特征空间的向量。
ELMK的目标是求该特征空间内的最优输出权重β,即求解

式中:ξi表示训练误差,C表示正则化系数。基于拉格朗日乘子法,最终ELMK的目标可以转换成
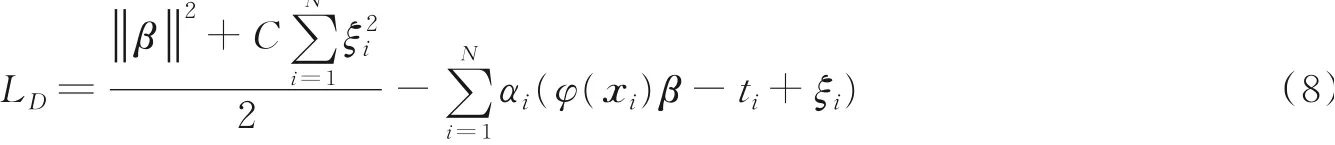
式中αi表示第i个拉格朗日乘子。
1.3 SIEL算法
SIEL算法作为一种基于自适应增量集成学习的通用框架,可以有效解决NS-FTSP问题。SIEL算法的主要思想是为每个NS-FTS子集增量地训练一个基模型,然后使用自适应加权规则将所有基模型组合起来。SIEL算法的重点在于数据权重和基模型权重的更新。图2展示了SIEL算法的基本流程。
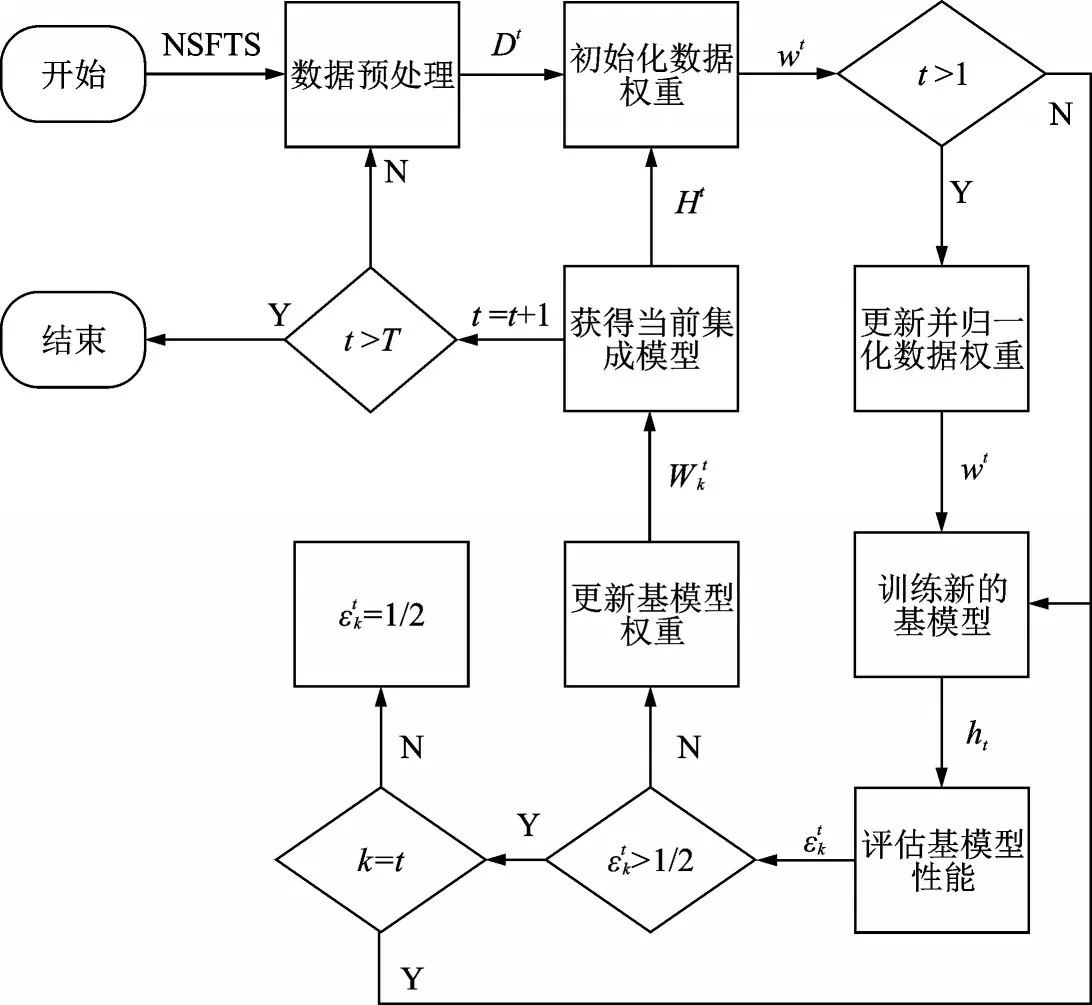
图2 SIEL算法的结构图Fig.2 Block diagram of SIEL algorithm
SIEL算法的具体步骤如下:
(1)数据预处理。首先,使用式(9)对非平稳金融时间序列NSFTS={d1,d2,…,dN}进行归一化处理,得到序列DATA。

式中:di表示原始数据,dmin表示原序列上的最小值,dmax表示原序列上的最大值,d′i表示归一化后的数据。然后,将DATA转 换为预测 任务所需的 训练集Train={(x1,y1),(x2,y2),…,(xn,yn)}和测试集Test={(xn+1,yn+1),(xn+2,yn+2),…,(xn+ts,yn+ts)},其中n=N-tw-ts,tw表示 时 间 窗大小,ts表示 测 试集大小。然 后 把Train分成T部分,得到Dt={(x1,y1),(x2,y2),…,(xmt,ymt),t=1,2,…,T},其中
(2)当新的数据子集Dt到来时,初始化数据分布。此时,所有数据的权重是相同的,即

(3)更新并归一化数据权重。首先,计算当前集成模型H t-1在Dt上的相对误差
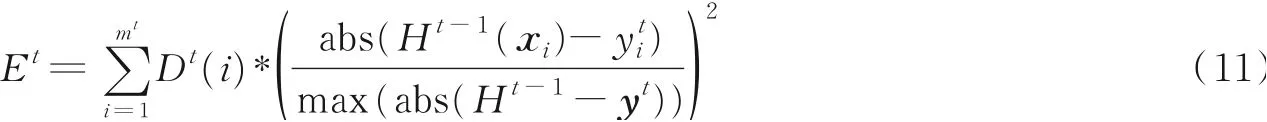
然后,根据Et更新数据权重
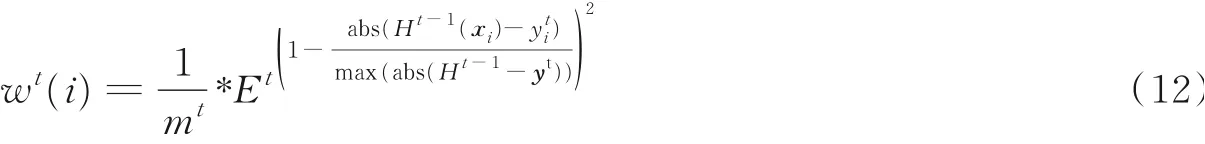
更新的数据权重不是为了数据采样,而是为了在式(14)中评估和均衡误差。最后,对wt(i)进行归一化处理,即

(4)在Dt上使用ELMK训练一个新的基模型ht,将其作为新的集成成员来增量地构建基模型集合。
(5)评估此时所有基模型hk(k=1,2,…,t)在Dt上的性能
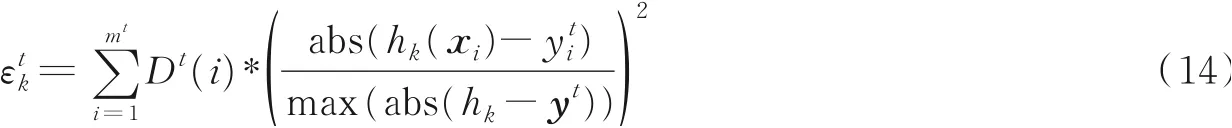
(6)计算所有基模型的加权平均误差以自适应地更新基模型权重并消除噪声对基模型的影响。首先根据式(15~17)对基模型的误差进行时间加权,以便为每个基模型在更新数据集下的性能分配到更大的权重值,然后根据式(18)计算各个基模型的权重。


(7)使用加权规则组合每个基模型,得到一个新的集成模型,即

这时,生成的集成模型H t将通过影响步骤(3)中数据权重的更新来影响基模型权重的更新。理想情况下,只要数据输入不中断,SIEL算法将会始终生成新的集成模型来适应下一个新环境。
2 实验设置和结果分析
2.1 实验数据集
本文使用3个FTS数据集来评估SIEL算法的性能:美元兑人民币汇率(USD/CNY)、上证综合指数(SSE)和日经指数(N225)。3个FTS数据集均从Yahoo finance[27]获得。由于并不是所有的FTS都具有非平稳特征,
因此出于严谨性考虑,在实验之前,使用增广迪基-福勒(Augmented Dickey-Fuller,ADF)[28]检验方法对这3个FTS数据集进行了非平稳检验,检验结果如表1所示。从表1可以看出,这3个FTS数据集都是非平稳的,均为NS-FTS数据集。

表1 各数据集的ADF检验结果Table 1 Results of ADF test on each dataset
2.2 实验设置
2.2.1 算法参数设置
SIEL算法主要涉及3个参数:时间窗大小tw、子数据集数目T和基模型ELMK的核函数Kernel。tw和T过大过小都会对模型的泛化性能产生负面影响,因此需要对其进行合理设置。通过实验发现,对于所选数据集,tw在6和16之间,T在2和6之间,SIEL算法可以获得比较好的预测效果。此外,关于Kernel,经过交叉验证[29]可证明高斯核函数是比较好的选择。
2.2.2 对比算法设置
为进一步证明SIEL算法的性能,选取了5个对比算法:在线极限学习机(Online sequential ELM,OS-ELM)[30]、改进的误差最小化在线极限学习机(Online sequential improved error minimized ELM,OSIEM-ELM)[31]、双增量学习算法(Double incremental learning,DIL)[32]、核极限学习机(ELMK)和以ELM为基模型的SIEL算法(SIEL based on ELM,SIEL-ELM)。
OS-ELM和OSIEM-ELM都属于在线极限学习机,可以逐段或逐块地学习数据。DIL算法类似于本文提出的SIEL算法,它们都属于IL和EL算法。与DIL算法进行比较,可以验证SIEL算法能否更好地解决NS-FTSP问题。与SIEL-ELM算法和ELMK算法相比,可以验证SIEL中提出的基于自适应增量集成学习的通用框架对于算法性能的改善是否具有显著效果。
2.2.3 性能指标设置
为了评估SIEL算法和各个对比算法的性能,选取了两个性能指标:均方根误差(RMSE)和平均绝对误差(MAE)。

式中:xi代表数据的真实值代表数据的预测值;n表示数据集的大小。
为减少偶然因素对实验结果的影响,进行了20次独立重复实验。
2.3 实验结果
表2 和表3展示了SIEL算法在其参数tw、T取不同值时在各数据集上的RMSE结果,其中最小值以粗体显示。从结果可以看出,tw和T过大或过小都会对模型的泛化性能产生负面影响。针对本文的3个NS-FTS数据集,tw的合适范围为[6,16],T的合适范围为[2,6]。

表2 取不同tw值时SIEL算法在各数据集上的RMSE结果Table 2 RMSEs obtained by SIEL algorithm at different values of tw on each dataset

表3 取不同T值时SIEL算法在各数据集上的RMSE结果Table 3 RMSEs obtained by SIEL algorithm at different values of T on each dataset
表4 和表5分别展示了不同算法在各数据集上的RMSE和MAE结果。从表中可以看出,SIEL算法在每个数据集上的预测性能均优于其他算法,证明SIEL算法能更好地解决NS-FTSP问题。此外,SIEL、SIEL-ELM和ELMK这3种算法之间的比较,值得注意。从实验结果可以看出,SIEL算法和SIEL-ELM算法之间的RMSE比ELMK的RMSE更接近且更小。因此可以得出结论,SIEL算法中提出的基于自适应增量集成学习的通用框架对于算法性能的改善具有显著效果。

表4 不同算法在各数据集上的RMSE结果Table 4 RMSEs obtained by different algorithms on each dataset

表5 不同算法在各数据集上的MAE结果Table 5 MAEs obtained by different algorithms on each dataset
表6 展示了SIEL算法和对比算法之间关于RMSE和MAE的t-测试结果。从表中可以看出,与ELMK、DIL、OSELM和OSIEM-ELM算法相比,在5%显著性水平下,SIEL算法在实验数据集上的预测性能得到了显著改善。但是SIEL算法与其变种算法SIEL-ELM之间的t-测试结果存在H=0,这是因为与基模型的选择相比,SIEL中提出的基于自适应增量集成学习的通用框架更有利于算法性能的提高,基模型的选择相对不太重要。

表6 SIEL和其他对比算法的t⁃测试结果Table 6 t⁃test results between SIEL and other comparative algorithms
为了更直观地展示实验结果,分别在3个NS-FTS数据集上绘制了各算法的预测结果图。图3~5展示了各算法在USD/CNY、SSE和N225数据集上的预测值和实际值,其结果作了归一化处理。
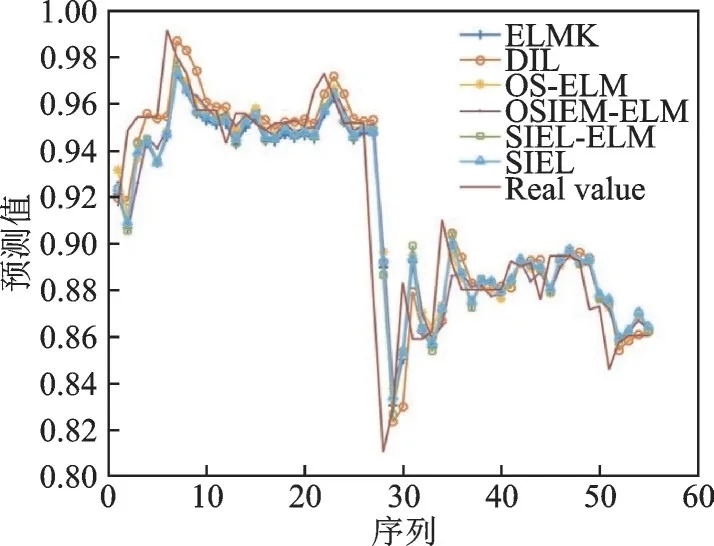
图3 不同算法在USD/CNY数据集上的预测结果Fig.3 Prediction results of different algorithms on USD/CNY dataset
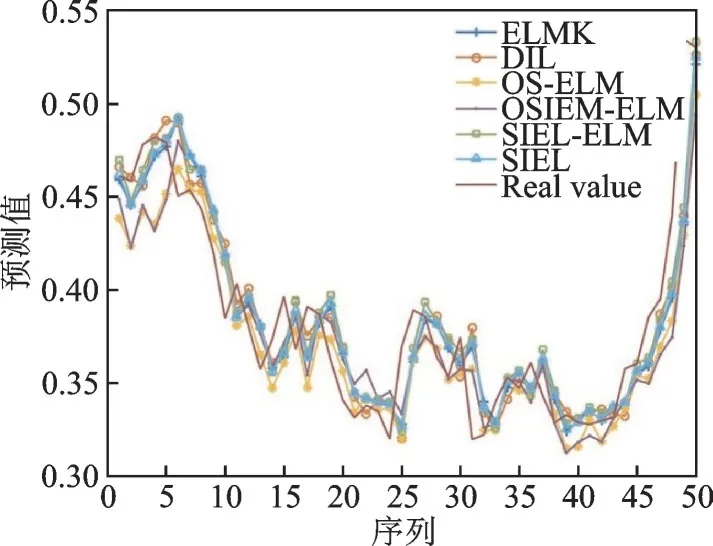
图4 不同算法在SSE数据集上的预测结果Fig.4 Prediction results of different algorithms on SSE dataset
从图3~5可以看出,各算法的预测趋势与实际趋势基本一致,但SIEL算法的预测趋势与实际趋势最接近。这也意味着SIEL在某种程度上缓解了“稳定性-可塑性”困境,从而能有效解决NS-FTSP问题。
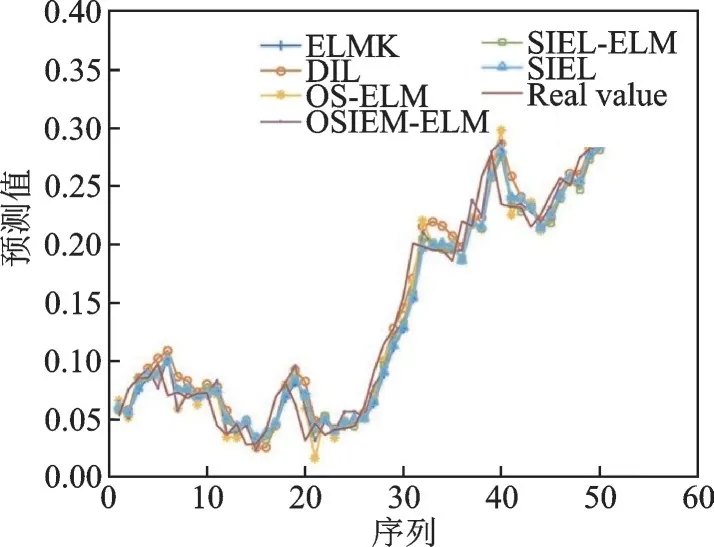
图5 不同算法在N225数据集上的预测结果Fig.5 Prediction results of different algorithms on N225 dataset
3 结束语
本文提出了一种基于自适应增量集成学习的方法SIEL来解决NS-FTSP问题。SIEL算法为每个NS-FTS子集增量地训练一个基模型,并使用自适应加权规则将它们组合在一起。实验证明,SIEL算法在解决NS-FTSP问题上取得了令人满意的结果。
但是SIEL算法仍存在一些不足。例如,每个基模型的训练过程都是独立的,这与在IL中充分利用历史知识的想法相矛盾。下一步的计划是使用“迁移学习”来加强基模型之间的关系并引入“剪枝”技术来更新基模型数量,以进一步改善算法性能。
