薄片炸药作用于波纹板防爆墙时的流场压力分析
2021-10-27张世联
罗 放,张世联
(上海交通大学 高新船舶与深海开发装备协同创新中心 海洋工程国家重点实验室,上海 200240)
海洋平台防爆墙的用途是通过吸收爆炸能量来减少对人员与设备的冲击影响。均布冲击载荷是海洋平台上的重要爆炸冲击形式,因此目前常用的爆炸计算规范如NTO等采用均布压力作为爆炸冲击载荷进行计算。在较小的均布压力载荷下,波纹板防爆墙通常表现出整体弯折现象,但是在均布冲击试验中,较小的冲击压力依然呈现出面板中拱的现象[1],如图1所示。因此在小当量冲击情况下按照规范计算所做的结构设计存在隐患。

图1 波纹板防爆墙试验与仿真计算结果[1]Fig. 1 Experiment and simulation result of corrugated blast wall
通过薄片炸药爆炸产生均布冲击载荷是种有效的近似试验方法。目前以薄片炸药作为研究方法的试验已有开展。Yuen等[1]开展了薄片炸药作用在不同加筋方式的方板后变形影响试验。Henchie等[2]则研究了薄片炸药对圆板的变形影响。这些试验着重研究钢板的变形,对爆炸时的流场压力变化关注较少[3],而流场研究的关注对象基本局限在球形炸药形式。年鑫哲等[4]对空气冲击波作用于防爆墙的透射和绕射效应展开分析,通过研究4种不同药量冲击波下压力流场的变化,得到了压力场的分布规律。穆朝民等[5]研究了圆柱形室内受到爆炸冲击时的流场压力变化。文虎等[6]对泄爆口强度对流场压力的影响做了研究。Ashkan等[7]对冲击管道中的爆炸压力波进行了机理分析。Mehreganian等[8]则对两种不同材料的钢板做了局部冲击压力下的变形对比。Orescanin等[9]将爆炸产生流场压力应用在了火山喷发研究中。这些研究均对爆炸流场中的压力分布与变化进行了相应的分析,但是针对薄片炸药所产生的均布冲击压力变化机理研究尚未开展。
通过流固耦合仿真方法对薄片炸药产生的均布冲击波进行计算,具体研究了自由边、槽型区域和连接构件及其周围的流场压力变化情况并分析其原因。在此基础上定量分析了薄片炸药量和槽型深度变化对流场压力和防爆墙变形的影响。
1 防爆墙的设计方案
1.1 波纹板防爆墙
文中研究的模型结构与文献[10]的1∶4缩比试验模型一致,海洋平台的波纹板防爆墙由波纹面板和连接构件组合构成,布置如图2(a)所示。波纹面板的厚度为2 mm,由不锈钢材料制作,如图2(b)所示。波纹面板的两边通过连接构件固定,而另两边为自由边。连接构件由厚度为4 mm、3 mm和12 mm的不锈钢角钢连接而成,不同角钢之间连接方式如图2(c)所示。整体防爆墙质量为41.5 kg[10-11]。
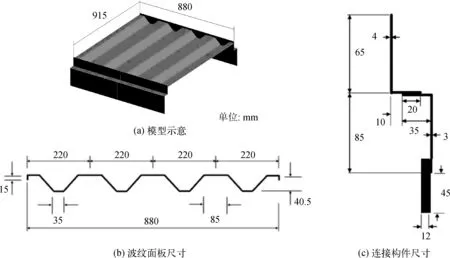
图2 波纹板防爆墙结构示意Fig. 2 corrugated blast wall diagram
1.2 流固耦合模型
薄片炸药的爆炸冲击计算采用流固耦合算法。在采用流固耦合法的数值计算中,需要使欧拉体和拉格朗日体互相作用。该算法中的欧拉体采用空间运动坐标,适用于爆炸冲击时的流场运动描述。而拉格朗日体在初始时将生成接触面,用于传递互相作用的应力速度材料等,达到与欧拉体之间的耦合效果。
对波纹板防爆墙建立有限元模型,如图3所示。模型由拉格朗日单元构成,面板厚度为2 mm,与图2的试验方案一致。单元数量为7 806。模型的底部采用固支方式,表示底部的连接构件刚性固定。在计算流固耦合时,需要将防爆墙与空气接触的耦合面设置为封闭区域,因此需要建立虚单元与防爆墙形成封闭的耦合面。图3中测点1至测点5用于计算流场压力数值变化。
图3中空气由六面体网格欧拉单元构成,边界条件设置为自由流动。每个单元尺寸的长宽高均为30 mm。与炸药接触的部分欧拉单元需要细化,以保证薄片炸药计算精度,单元细化高度为0.155 mm。
图3中防爆墙底部方形部分为薄片炸药。炸药与波纹面板设置的距离为160 mm。为研究冲击压力变化和防爆墙塑性变形的关系,将爆炸强度控制在防爆墙模型发生塑性大变形,但不完全炸裂。经试算,炸药的初始质量设置为2 g,其长宽为915 mm×880 mm,覆盖整个防爆墙区域。由炸药密度得到薄片炸药初始高度为0.155 mm。

图3 防爆墙流固耦合计算模型Fig. 3 Fluid-Solid coupling model of corrugated blast wall
1.3 材料参数
试验中防爆墙由不锈钢材料制成,计算中采用Cowper-Symonds屈服模型,该模型适合描述不锈钢材料的大变形与高应变度的变化,材料模型和参数与文献[10]一致,如表1所示,表中E为弹性模量,ν为泊松比,ρsteel为钢材密度,σb为破断应力,εr为伸长率。

表1 不锈钢的材料参数Tab. 1 Material parameters of steel
(1)

计算采用理想气体状态方程,可表示为:
(2)
式中:ρair为空气密度,ρ0为初始气体密度,Eair为空气内能,γ为空气比热容,各参数见表2[3]。
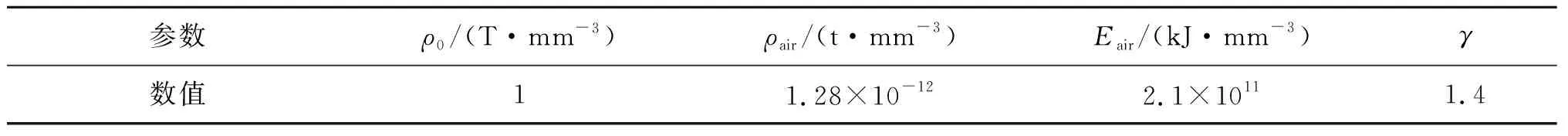
表2 空气的气体材料参数Tab. 2 material parameters of air
炸药采用理想化的整体引爆,其快速膨胀现象可采用JWL(Jones-Wilkins-Lee)方程描述。
(3)
式中:Eexp为炸药比内能,A、B、R1、R2、ω为常数,υ为爆速。各材料参数见表3[3]。

表3 炸药的JWL材料参数Tab. 3 JWL material parameters of explosion
2 计算结果
2.1 自由边界压力耗散
薄片炸药爆炸载荷下防爆墙的压力时历曲线如图4所示。由图4可知,防爆墙面板上的测点1至测点5的压力峰值基本出现在相同时刻0.15 ms,且除自由边的测点3以外所有测点的压力峰值较为接近,符合试验中薄片炸药产生均布冲击载荷的实际情况。而测点3的压力峰值远小于其它测点的压力峰值。这是由于防爆墙的自由边没有任何结构阻挡爆炸所产生的气体,气体压力在自由边的耗散现象较为显著,如图5中0.15 ms时刻所示。
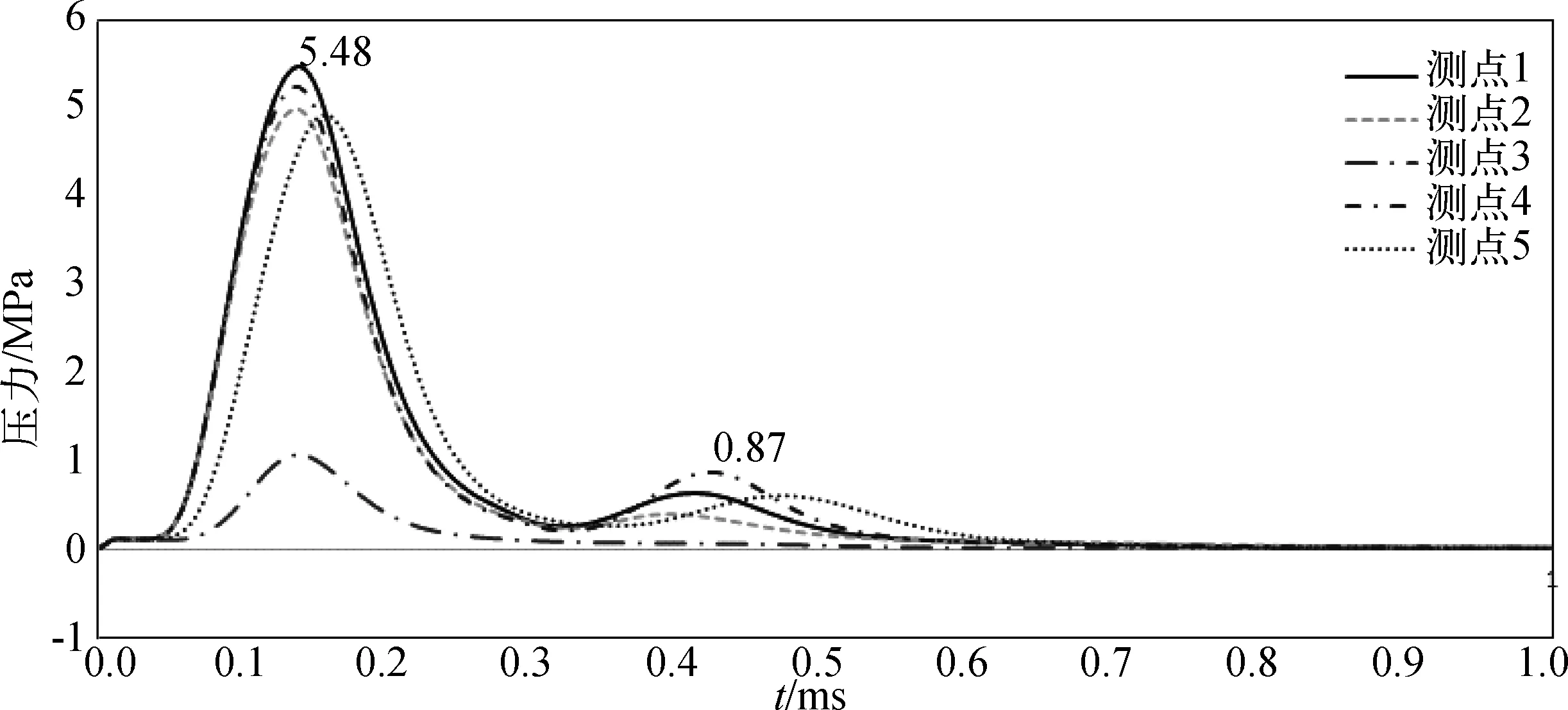
图4 薄片炸药爆炸载荷下防爆墙的压力时历曲线Fig. 4 Pressure history of blast wall under thin explosive
防爆墙和1/4空气模型中压力分布变化如图5所示。图5中0.05 ms为薄片炸药爆炸初始时刻,可以观察到空气模型中的冲击压力较为平均。而当0.15 ms时气体开始接触到防爆墙,自由边上的压力降低得非常明显,测点3的压力已远小于其它测点。

图5 防爆墙和1/4空气模型中压力分布变化Fig. 5 Variation of pressure distribution in blast wall and 1/4 air model
2.2 第二次压力峰值
由图4可知,防爆墙上的压力在0.35 ms至0.50 ms出现了第二次冲击压力峰值。波纹板防爆墙的槽型结构和连接构件造成了爆炸气体对防爆墙的第二次冲击压力。如图6所示,在0.35 ms时,部分爆炸冲击气体遇到连接构件受阻后向波纹面板中心反弹。反弹气体中的一部分被滞留在面板上,面板的槽型结构使滞留的气体开始聚集,由此形成第二次压力峰值,直到0.45 ms后才开始耗散,逐渐恢复至空气常值。从波纹面板上的压力分布可知,波纹面板中部的槽型区域第二次冲击压力峰值最大,其压力分布明显高于其它槽型区域,这将使波纹面板形成中拱现象。
2.3 连接构件上的冲击压力
连接构件在冲击载荷下同样受到气流的反弹冲击,连接构件测点的压力和变形如图7所示。连接构件测点上的压力峰值出现在0.35 ms,与图6上防爆墙连接构件上的压力分布变化一致。该测点的位移在初期出现宽幅振荡,随后稳定在0值附近。这是由于波纹面板在受到冲击后开始弯曲,使得连接构件沿x向内收变形。而爆炸所产生的冲击压力使构件向扩,由此形成了爆炸初期的巨幅振荡。而爆炸后期连接构件在0值附近趋于稳定也反映出该冲击压力并未对连接构件的最终变形造成明显影响。

图6 第二次冲击时防爆墙和1/2空气中压力分布变化Fig. 6 Variation of pressure distribution in blast wall and air during second shock

图7 连接构件测点压力和变形时历曲线Fig. 7 Pressure and deformation history of connection measuring point
3 流场压力影响因素
影响均布冲击流场压力的主要因素由薄片炸药和受冲结构的形状两个部分组成,因此从炸药质量和槽型深度两个角度进行定量分析。
3.1 薄片炸药质量
对于薄片炸药而言,炸药厚度可以通过调整炸药质量来控制实现。图8比较了4种不同薄片炸药量(2 g至8 g)下测点1的压力时历曲线,这些曲线都出现了明显的两次压力峰值增幅。由图8可以发现,两次压力峰值随炸药量增加而提高,而且压力峰值出现时间更为提前,其中第二次压力峰值增幅明显大于第一次压力峰值。图9所示为测点1的第二次压力峰值与第一次压力峰值的比值。随着薄片炸药质量的增加,第二次压力峰值从不足第一次峰值的1%增加至45%。这表明随着第一次冲击压力的增加,被反弹滞留在槽型区域内的压力相应提高,由此造成的波纹面板中拱现象愈加显著。

图8 不同药量下测点1压力时历曲线Fig. 8 Pressure history of Point 1 with different explosive contents

图9 不同药量下测点1的两次压力峰值比值Fig. 9 Mass of thin explosive vs pressure peak ratio of Point 1
为直观对比,选取质量为2 g和8 g的薄片炸药下波纹板防爆墙的永久变形,如图10和图11所示。第二次压力峰值从0.63 MPa增加至4.48 MPa,防爆墙中心位移从9.88 mm增加至214.00 mm。由2.2节分析可知,第二次压力峰值是由槽型滞留和边界耗散共同作用所造成,其表现为面板出现中拱现象。因此随着炸药量的增大,防爆墙整体垂向变形增加显著,并且波纹面板的中拱现象也愈加明显。这种中拱现象将对结构连接处产生撕裂倾向,如图11所示。
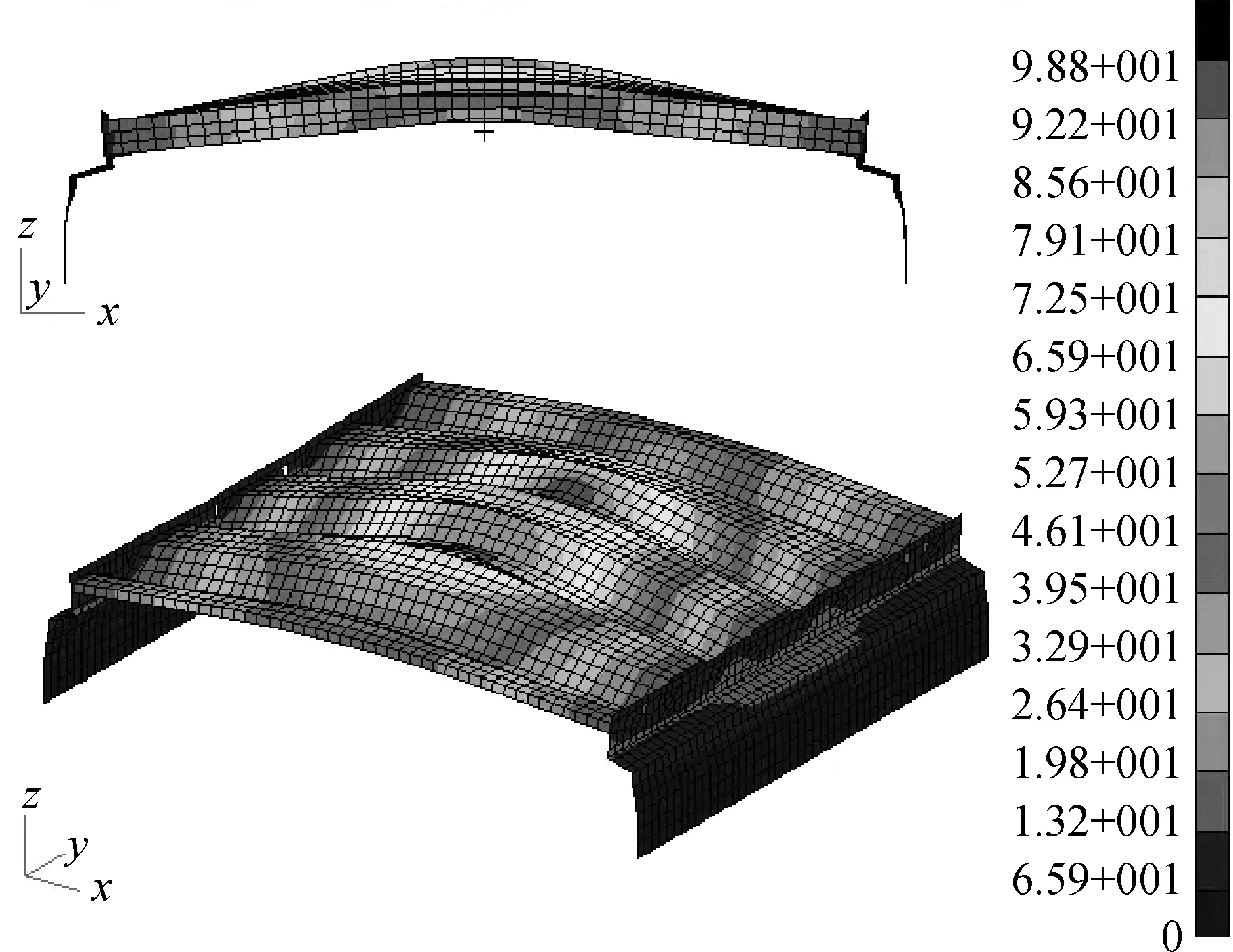
图10 质量为2 g薄片炸药时永久变形Fig. 10 Permanent deformation under 2 g thin explosive

图11 质量为8 g薄片炸药时永久变形Fig. 11 Permanent deformation under 8 g thin explosive
3.2 槽型深度
将槽型深度作为影响流场压力的研究对象,深度从原有的40.5 mm逐步增至80.0 mm,用8 g薄片炸药进行冲击计算,分析槽型区域对流场压力的影响。槽型深度D的变化如图12所示。

图12 槽型深度示意Fig. 12 diagram of groove depth
图13为不同槽型深度下测点1的冲击压力时历曲线。由图13可知,随着槽型深度D的增加,冲击压力峰值也随之提高。第一次压力峰值的放大程度为14.86%,第二次压力峰值的放大程度22.23%,而波纹板防爆墙的永久变形值从169 mm减小至100 mm,如图14所示。槽型深度的增加虽然使滞留的冲击气体更为聚集,从而放大冲击压力峰值,但是也增加了波纹面板的抗弯能力,提高了防爆墙整体的抗爆性能。
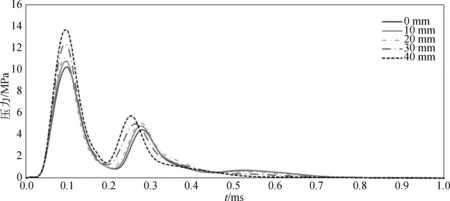
图13 不同槽型深度下测点1的冲击压力时历曲线Fig. 13 Pressure history of Point 1 with different groove depths
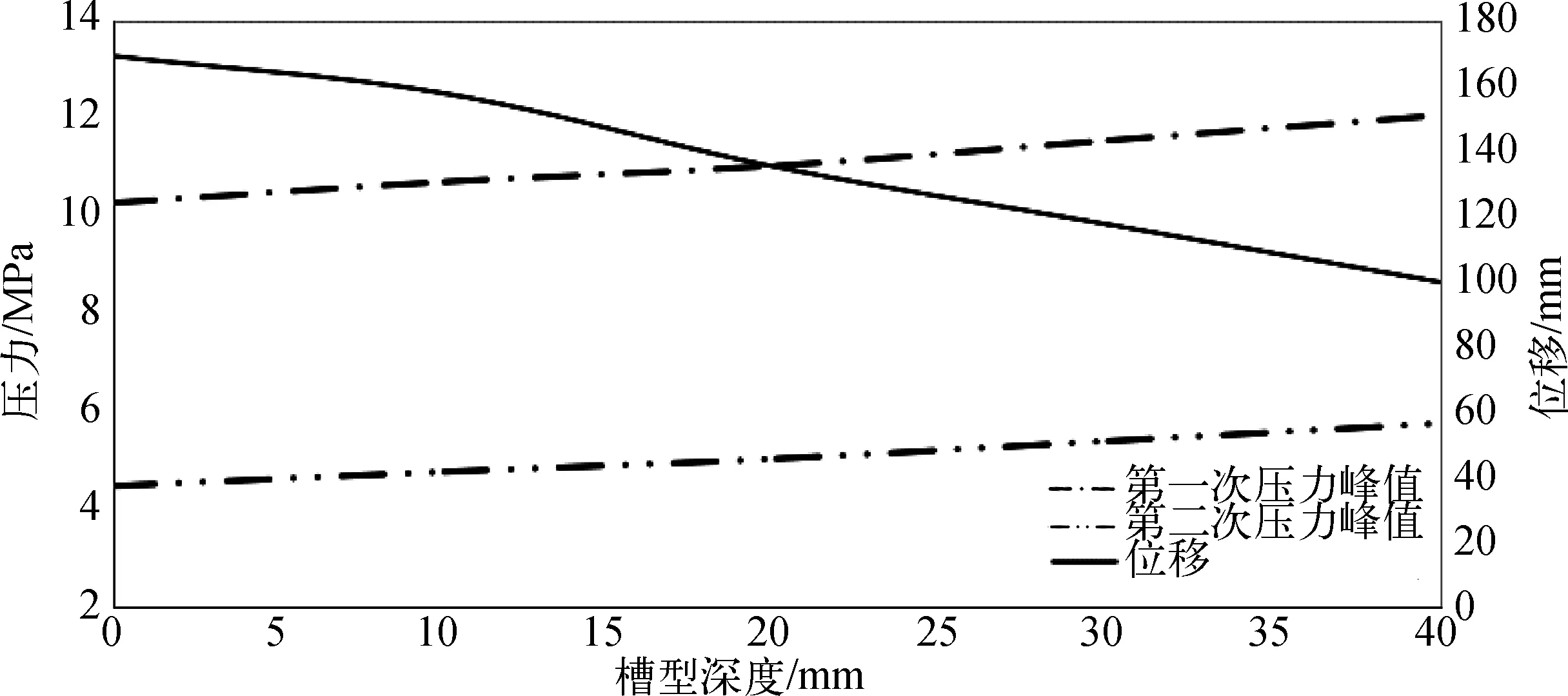
图14 槽型深度变化对测点1的压力峰值和位移影响Fig. 14 Groove depth vs pressure peak and deformation of Point 1
4 结 语
通过计算薄片炸药爆炸所产生的均布冲击,分析了流场压力变化对波纹板防爆墙的冲击影响,研究了炸药量和槽型深度对流场压力变化的影响因素,并得到以下结论:
1) 波纹板防爆墙在受到均布冲击载荷时,槽型结构的滞留效应和自由边的压力耗散使得波纹面板出现第二次压力峰值,造成了波纹面板的中拱现象。该现象更接近实际试验结果。
2) 随着薄片炸药质量的增加,波纹面板的第二次峰值压力显著提高,面板的中拱现象也更加明显,进而导致面板连接处出现撕裂倾向。
3) 波纹板槽型深度增加虽然会增加槽型滞留效应和结构整体质量,但也提高了波纹面板的整体抗弯性能,从而为降低板厚而保持抗爆性能的结构优化设计留下余量。
