基于不完全正交的WIGMRES(m)算法
2021-10-27于春肖井丁卉杨艳芳
于春肖,井丁卉,杨艳芳
(燕山大学 理学院 河北 秦皇岛 066004)
0 引言
在工程领域中,很多问题最终都可归结为求解大型线性方程组。由Sadd提出的GMRES(m)算法是求解大型线性方程组最有效的方法之一,被广泛应用到工程领域[1-4]。随着GMRES(m)算法的广泛应用,为加快GMRES(m)算法的收敛速度,很多学者对该算法进行优化与改进,一种方法是采用预处理技术[5-7],通过加权技术,即WGMRES(m)算法来加快算法的收敛性。孙蕾等利用残量多项式预处理方法,建立右端多项式预处理GMRES(m)算法[8];于春肖等通过深入探讨算法的收敛性与方程组系数矩阵的密切关系[9],提出一种预条件广义极小残余新算法;杨圣炜等通过引用加权技术,提出了加权SGMRES算法(WSGMRES算法)[10];在此基础上,仲红秀等利用加权策略和分析基底条件数,对块simple GMRES方法进行了改进,提出加权simple GMRES算法[11];Yu等通过改变m的取值来加快收敛,进而提出VRP-GMRES(m)算法[12-13];郝雪景等利用截断技术,基于不完全正交的Arnoldi过程提出截断型变参数广义极小残余算法(VRP-IGMRES(m))[14]。本文利用截断技术[15-16],提出一种不完全正交的WIGMRES(m)算法,并结合数值算例,分析该算法的高效性。
1 WGMRES(m)算法

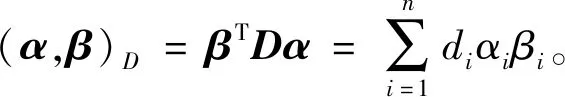
加权Arnoldi过程:
1)取v1=r0/‖r0‖D;
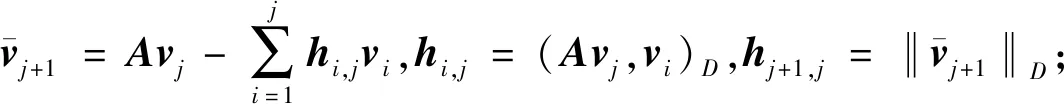

结合GMRES(m)算法和加权Arnoldi过程,WGMRES(m)算法计算步骤如下:
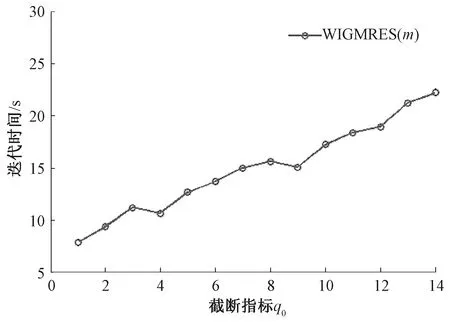
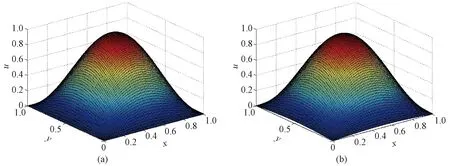
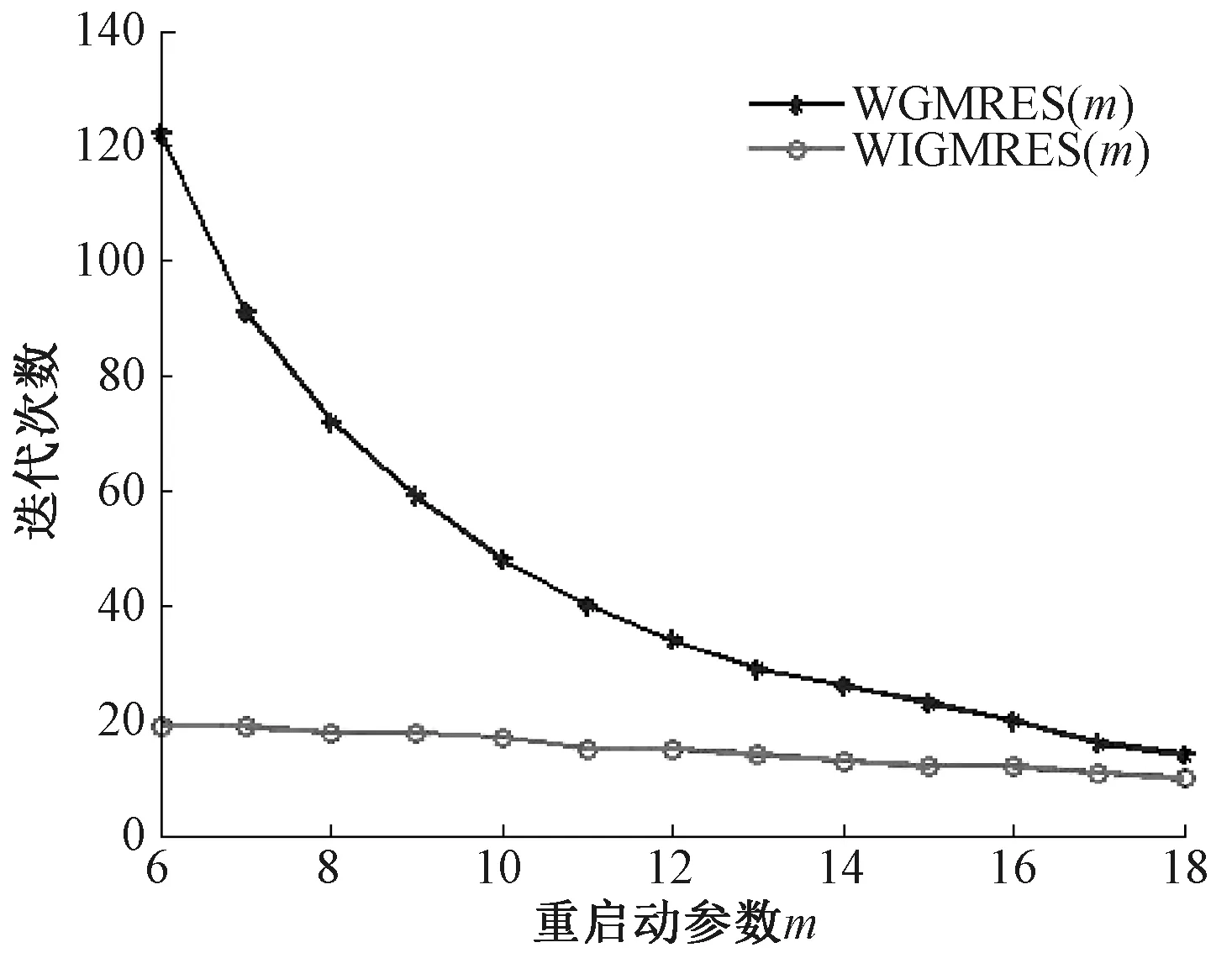
1)选取x0∈Rn,m∈N+(m 5)若‖rm‖=‖r0-Azm‖<ε,则x=xm,迭代停止,否则x0=xm,转向步骤2)。 当m很大时,考虑到在构造krylov子空间的基向量和Hessenberg矩阵时要用到长递推公式,导致算法计算量和存储量过大,因此在WGMRES(m)算法的基础上进行改进,提出一种新型截断型算法,即WIGMRES(m)算法,该算法仅对Avj前面的至多q个向量进行正交,vj0,…,vj,j0=max{1,j-q-1}正交,其中q 1)选取x0∈Rn,m∈N+(m (1) 4)求解最小二乘问题 (2) 得ym,其中e1=(1,0,…,0)T∈Rm+1; 5)构造近似解,xm=x0+Vmym; 6)计算残余向量的模,‖rm‖=‖b-Axm‖; 7)重启动判断,若‖rm‖<ε,则精确解x=xm,迭代停止;否则,置x0=xm,m=m+1,转2)。 为证明算法WIGMRES(m)的收敛性态,本文将WIGMRES(m)算法和WGMRES(m)算法联系起来,证明WIGMRES(m)的收敛性,为方便讨论,令WIGMRES(m)算法的残余向量的模为rm(WIG),WGMRES(m)算法残余向量的模为rm(WG)。 定理1假设Vm+1列满秩,则WIGMRES(m)算法和WGMRES(m)算法在Km(r0,A)上的残值范数满足 ‖rm(WIG)‖≤S(Vm+1)‖rm(WG)‖, (3) 证毕。 算例1考虑一维波动方程 (4) 方程(4)的精确解为u(x,y)=sin(πx)e-π2y+sin(3πx)e-9π2y,如图1(a)所示。将区域沿x方向和y方向n等分,其中采用隐式差分法求解方程(4),可得方程组 u(x,y)=sin(πx)e-π2y+sin(3πx)e-9π2y。 取n=20,m=10,q0=9时,用WIGMRES(m)算法求解一维波动方程,计算结果如图1(b)所示。由图1知,问题(4)的数值解和精确解是一致的,说明WIGMRES(m)算法的正确性。 取n=30,m=15考虑截断指标q0在1~14内取值,得到截断指标对残余范数和计算时间的图像如图2、3 所示,残余范数随着截断指标的增大波动后趋于平缓,计算时间随着截断指标的增大而缓慢增大,说明截断指标越小,截断效果越明显。 图2 截断指标对残余范数的影响Figure 2 Effect of truncation index on residual norm 图3 截断指标对计算时间的影响Figure 3 The impact of truncation indicators on calculation time 算例2考虑二维泊松方程 (5) 其中:Ω={(x,y)|0 方程(5)的精确解为u(x,y)=sin πxsin πy,如图4(a)所示。将区域沿x方向和y方向n等分,其中采用五点差分法求解方程(5),可得方程组取n=100,m=10截断指标q0=9时,用WIGMRES(m)求解二维泊松方程的数值解如图4(b)所示,根据图4可知,数值解与精确解一致,因此说明算法WIGMRES(m)的正确性。 图4 温度分布Figure 4 Temperature distribution Ax=b,A∈R(n-1)2×(n-1)2,x,b∈R(n-1)2。 取n=50,q0=5时,且m在4~14内取值,当重启动参数取不同的值时,GMRES(m)算法、WGMRES(m)算法和WIGMRES(m)算法的数值结果如表1、2所示,当参数m发生变化时,GMRES(m)算法的迭代次数最多,WGMRES(m)算法次之,WIGMRES(m)算法最少且WIGMRES(m)算法的计算精度最高,由此证明WIGMRES(m)算法在保证精度的情况下计算效率大大提高。 表1 m取不同值时三种算法的迭代次数比较Table 1 Comparison of the number of iterations of the three algorithms with different values of m 表2 m取不同的值时三种算法的计算精度比较Table 2 Comparison of the calculation accuracy of the three algorithms with different values of m 取n=40,q0=5,且m在6~18内取值,执行WIGMRES(m)和WGMRES(m)两种算法,当重启动参数m取不同值,得到两种算法的迭代时间和迭代次数变化(图5、6)。根据图5、6可知,新算法WIGMRES(m)更加稳定,且以较高的精度快速收敛。当m=10时,不同网格下的两种算法的计算时间如表3所示,表格显示随着n的不断增大,相同网格下,WIGMRES(m)算法总比WGMRES(m)算法的计算时间少,由此说明,WIGMRES(m)算法的优越性。 图5 两种算法迭代次数的比较Figure 5 Comparison of the number of iterations of the two algorithms 图6 两种算法迭代时间的比较Figure 6 Comparison of iteration time of two algorithms 表3 不同网格下两种算法计算时间的比较(m=10)Table 3 Comparison of calculation time of two algorithms on different grids (m=10)单位:s 本文在WGMRES(m)算法的基础上,通过采用截断技术,提出WIGMRES(m)新算法,并证明该算法的收敛性。通过数值算例证明WIGMRES(m)新算法得出的结果与精确解十分吻合,证明了该算法的有效性。同时当参数m取不同值时三种算法的迭代次数和计算精度的变化情况,以及WIGMRES(m)和WGMRES(m)两种算法对计算效率和计算精度的影响,结果表明新算法在计算效率和计算精度方面均有很大提高。
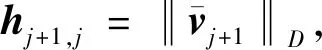
2 WIGMRES(m)算法

3 WIGMRES(m)算法的收敛性

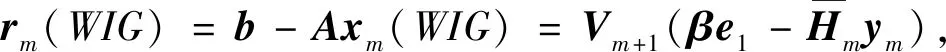

4 数值算例





5 结论
