An advanced five-unknown higher-order theory for free vibration of composite and sandwich plates
2021-10-27ZhenWURuiMAYongzhiLIYushanXIAOJieMEI
Zhen WU, Rui MA, Yongzhi LI, Yushan XIAO, Jie MEI
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
KEYWORDS Analytical solution;Five-unknown;Free vibrations;Higher-order theory;Sandwich plates
Abstract Accurate prediction of dynamic characteristics is quite critical to understand the strength of layered structures. Nevertheless, the existing five-unknown higher-order theories encounter difficulties to forecast accurately the dynamic response of sandwich structures. Therefore, a new five-unknown higher-order theory is developed for free vibration analysis of composite and sandwich plates, which possesses the same degree of freedom as those of other five-unknown higherorder theories. The developed model can meet beforehand interlaminar continuity conditions and the free-surface conditions of transverse shear stresses.To assess capability of the proposed model,analytical solution for such composite structures with simply-supported conditions has been presented by employing Hamilton’s principle, which is utilized for analysis of mechanical behaviors of composite and sandwich plates. Compared with the three-dimensional (3D) elasticity solutions,3D finite element results and the results obtained from the chosen five-unknown higher-order models,the proposed model can yield accurately natural frequencies of composite and sandwich plates.Even for the thick plates, the higher-order frequencies calculated from the proposed model are in good agreement with the 3D finite element results.By studying effect of the thickness/length ratios on natural frequencies, it is found that the proposed model is adaptable to predicting natural frequencies of the sandwich plates with the thickness/length ratios between 1/4 and 1/100.In addition,some factors influencing accuracy of five-unknown higher-order models have been investigated in detail. Finally, by means of numerical analysis and discussion, some conclusions have been drawn as well, which can serve as a reference for other investigators.
1. Introduction
Due to the excellent mechanical characteristics, layered composite structures are extensively adopted in many engineering fields including aerospace vehicles,underwater space and shipbuilding. The shear deformation effects of laminated composite and sandwich laminates under transverse loads are very significant.For reliable and safe designs,it is necessary to well understand the static and dynamic behaviors of laminated structures. Thus, the reliable models must be established to accurately predict the responses of laminated structures.
The traditional theory such as First-order Shear Deformation Theory (FSDT)was widely applied to analyze the mechanical behaviors of laminated structures,sandwich structures and Functionally Graded Material (FGM) structures,attributing to its simplicity and high efficiency. However,transverse shear strain cannot satisfy the free surface condition, so the FSDT will encounter difficulty to accurately predict the mechanical response of sandwich plates.
In order to overcome the aforementioned issues, a variety of higher-order shear deformation theories have been proposed to predict the bending,dynamic and buckling behaviors of composite structures. By considering the stretching effect,Mukhtarutilized two types of methods to obtain the analytical solution of free vibration of orthotropic panels, which composed of three combinations of boundary conditions.Subsequently, various factors such as material parameters, geometric and boundary conditions were investigated in detail.Arefi et al.used the concept of neutral surface integrated with piezoelasticity relations concept for natural frequency analysis of Functionally Graded (FG) sandwich nano-plate. Through improving the FSDT, Nguyen et al.obtained analytical solutions of the bending behaviors and natural frequencies of simple-supported FGM plats. By using Navier’s method, the analytical solution of thermal critical load of symmetric three-layer beam subjected to uniform temperature was obtained by Bouazza et al.Subsequently, a variety of factors on thermal buckling response have been taken into consideration as well. Considering the viscoelastic properties of the micro plates, the nonlinear dynamic buckling of temperature dependent nanocomposite rectangular structures was studied by Shokravi and Jalili.In the study of Vu et al.,the mechanical behavior analysis of thick and thin composite FGM plates was investigated with the technique of the moving Kriging interpolation method.Do and Leepresented a quasi 3D isogeometric method for dynamic analysis of square or circular FGM plates with three types of cutouts.
With respect to the research work on five-unknown Higherorder Shear Deformation Theories(HSDTs),a family of models have been developed. Reddyproposed a simple HSDT containing five unknowns, and the transverse shear stresses calculated from such model are parabolic distribution along thickness direction.What’s more,the Reddy’s model can guarantee the free surface conditions.Mantari et al.developed an analytical solution to calculate the bending behaviors and natural frequency of simple-supported isotropic plates, cross-ply cylindrical and spherical shells under three types of loads. By introducing a hyperbolic function into the higher-order displacement model, Mahi et al.analyzed the mechanical response of multilayered plates and shells.Based on a modified FSDT, the natural frequency of multilayered sandwich plates and shells was studied by Hwu et al.using Navier’s technique, Levy’s approach and Ritz method. Singh and Singhrecommended two types of displacement models namely trigonometric HSDT and trigonometric-hyperbolic HSDT to predict the mechanical response of layered and 3D braided composite plates. Based on Reddy’s model, Zamani et al.investigated natural frequency of simply-supported laminated plates on Pasternak viscoelastic medium through derivation of kinematic equilibrium equation integrating Laplace transform with Hamilton principle. Al-shujairi and Mollamahmutog˘luinvestigated the dynamic behavior of the FGM micro-beam resting on two types of elastic foundations,namely Winkler and Pasternak.Shi et al.developed a hyperbolic tangent HSDT integrating with isogeometric analysis to analyze mechanical behavior of the simple-supported laminated plates. Kant and Swaminathanapplied generalized higher-order theory to obtain closed-form solutions for the free vibration analysis of composite and sandwich plates. Biswal and Mohantypresented a kind of shell element for analysis of the damping characteristics and natural frequency of sandwich spherical shell structures. Natural frequency of FGM porous square/circular plates with fully simplysupported and clamped boundary conditions was predicted by Nguyen et al.using isogeometric Finite Element Method(FEM) based on the Ctype HSDT. Hachemi and Hamza-Cherifdeveloped a new Cenriched curved quadrilateral pelement approach based on HSDT to study the natural frequency of angle-ply symmetric and antisymmetric composite square plate with an intricate cutout.Kumar et al.employed two types of HSDTs with five unknowns for the static analysis of FGM square plate. Meanwhile, they proposed a kind of method to discretize the governing differential equation. In addition, the theory proposed by Kumar et al.was used to calculate the natural frequency of angle-ply FGM plates subjected to uniaxial and biaxial compression based on meshless approach given by Shukla et al.
First-order perturbation technique has been employed by Tomar and Talhato investigate stochastic natural frequency and bending response of FGM sandwich panel using Reddy’s HSDT.By changing the shape function of in-plane displacement field, Mantari et al.proposed a HSDT to analyze natural frequency of simple-supported composite cylindrical and spherical shells.Grover et al.constructed the nonpolynomial shear-strain functions to study mechanical response of multilayered composite structures. By introducing panel and the core made up of metal/ceramic and ceramic respectively into sandwich structures, Sobhyanalyzed natural frequencies and critical loads of four types of FGM sandwich panels on Pasternak’s type elastic foundation. Some key effects of mechanical and physical properties on the mechanical responses of sandwich nano-plate under thermal, magnetic,electrical and mechanical loading can be observed in Ref..Javedcarried out a comparison analysis on natural frequencies of cross-ply simply supported shells by using HSDTs with five unknowns. Moreover, the influences of geometric parameters and material parameters on the mechanical behavior of conical shell are discussed as well.
Pandey and Pradyumnapresented an eight-node plate element based on a Clayerwise theory to study the mechanical behavior of laminated composite structures. Based upon generalized differential quadrature method and layerwise method,Tornabene et al.obtained the mode shapes of angle-ply laminated and FGM plates and shells. Hierarchical finite beam elements were constructed to solve the static problem of sandwich structures under simply-supported boundary conditions.Subsequently, such model was extended for dynamic analysis of 3D sandwich structures under different boundary conditions.The Clayerwise element was proposed for dynamic analysis of the composite and sandwich structures by Belarbi et al.What’s more, the influences of various factors on natural frequency were considered and the finite element results were verified by typical examples as well.
In addition,Yi et al.used the special HSDT for the static bending and dynamic analysis of thin and thick square plates under severe loadings. With the help of a novel mathematical formulation, Tornabene et al.researched the natural frequencies of multi-layered composite damaged structures.Mehar and Pandadeveloped a general third-order polynomial function combined with MATLAB code to examine the static bending problem of the multi-walled carbon nanotube reinforcement sandwich shell panel.Meanwhile,they provided the experimental results to examine the theoretical solutions.Kumar et al.recommended a HSDT coupled with a zigzag function to predict the first three critical buckling loads.Dastjerdi and Tadi Benistudied nonlinear bending behaviors of macro and nano sector plates.
Transverse shear and normal stresses have the significant effects on mechanical behavior of thick composite structures.In order to consider these impacts,Katariya et al.calculated the nonlinear behavior of multilayer composite structures. A refined and generalized quasi-3D zigzag beam theory was recommended by Han et al.to predict natural frequency of laminated beams under various types of load distributions. An isogeometric FEM model considering the shear deformation and thickness stretching effects was proposed by Tran and Kimto calculate mechanical response of plates with various shapes.Adhikari and Singhemployed an eight-node isoparametric serendipity element to analyze free vibrations response of FGM plates. Ganapathi et al.used the Newmark’s method to research the dynamic response of a porous nanocomposite beams.Adhikari and Singhdeveloped a simple quasi-3D theory with inverse trigonometric to analyze the free and forced vibration behavior of layered plates with several kinds of boundary conditions. At the same time, the temperature effect was also introduced to calculate natural frequencies of such structures.More investigations on dynamic behaviors of composite and FGM plate and shell can be found in Refs..
By review of literature, it is found that a number of fiveunknown higher-order theories have been employed for dynamic analysis of the laminated composite, sandwich and FGM structures. Nonetheless, the existing fiveunknown higher-order theories might encounter some troubles in analyzing dynamic response of sandwich structures.Therefore, a refined five-unknown higher-order theory will be developed for the dynamic analysis of the simplesupported composite and sandwich plates in the present work. The displacement field of the proposed model is the same as those of other five-unknown higher-order theories.Analytical solution for composite and sandwich plates have been presented by employing Hamilton’s principle, which is to be utilized for analysis of dynamic behavior of such structures. The 3D elastic theoryare chosen to assess the proposed method. Nevertheless, the 3D elastic theory referring to the present work is rarely reported in the published literature, so the 3D-FEM is employed to evaluate the proposed model in present work. The proposed model can yield more accurately natural frequencies in contrast with the results of 3D finite element method and the results obtained from other models. In addition, some factors influencing accuracy of five-unknown higher-order models have been investigated in detail, which can serve as a reference for other investigators.
2. Refined Five-unknown Higher-order Theory (RFHT)
Schematic figure for a sandwich plate is shown in Fig.1,where a represents the length,b represents the width,and h represents the thickness of plate.
Based on the assumption of Reddy’s HSDT,displacement field of the five-unknown higher-order model can be generally written as

where u,vand wdenote the displacement parts at a point on the mid-plane of plate along x,y and z directions,respectively;αand αare the rotations relative to y and x axes; f(z) represents the transverse shear deformation through thickness of plate. Different functions f(z) can determine various fiveunknown higher-order models, and the function f(z)proposed by Reddyis selected in the present work, which can be written as f(z)=z(1–4z/3h). In the 3D elasticity analysis,the first derivative of function f(z) relative to coordinate z is required to be discontinuous at the interface of adjacent layers,which can be used to meet the interlaminar continuity of transverse shear stresses. Thus, a novel shear function will be proposed to develop a RFHT.
After introducing the local displacement functions at each ply, the initial displacement field of the current theory is presented as

where ςis the local coordinate along thickness direction at the k th play, ς∈[-1, 1]; uand vare local displacement components which are composed of the polynomial of ς.
In present work, the local displacement functions are assumed to be parabolic distribution along thickness direction of each lamina, in which we can write it as


Fig. 1 Schematic figure for a sandwich plate.
In order to eliminate the local displacement parameters at each ply, the continuity conditions of in-plane displacements at the interfaces are firstly utilized.Subsequently,interlaminar continuity conditions and free-surface conditions of transverse shear stresses are further employed to reduce the local displacement variables,so it is required that the number n of total layers is more than 1.Finally,displacement field of the RFHT can be obtained as

where coefficients A and B can be determined by using the freesurface conditions of transverse shear stresses on the upper surfaces, which are presented by


Table 1 Chosen shear deformation functions in published literatures.

Fig. 2 Shear deformation functions through thickness of plate.
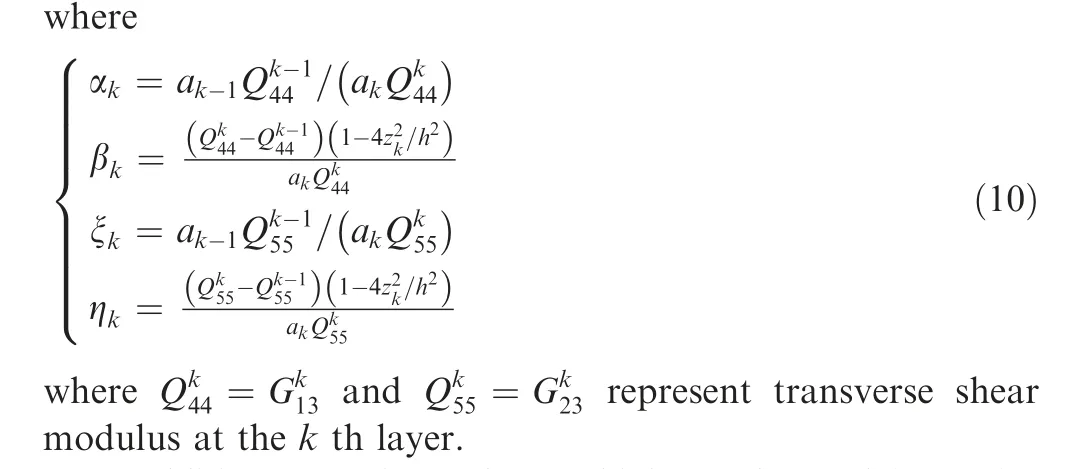
In addition,some five-unknown higher-order models are also chosen for comparison and assessment,which have been shown in Table 1. Several shear deformation functions are shown in Fig.2,which can be found that the shear deformation function of the model RFHT at the interfaces shows a sudden deflection,which is generally called as the zig-zag effect. Moreover, the derivatives of shear deformation functions relative to coordinate z through thickness of plate are depicted in Fig.3.Derivatives of shear deformation functions obtained from the RFHT are not continuous at interfaces,which can make transverse shear stresses to be continuous across the thickness of plate.
3. Analytical solution
To assess capability of the five-unknown higher-order model,analytical solution of laminated plates with simply-supported boundaries will be presented, which will be compared with 3D-FEM results and the exact solutions.
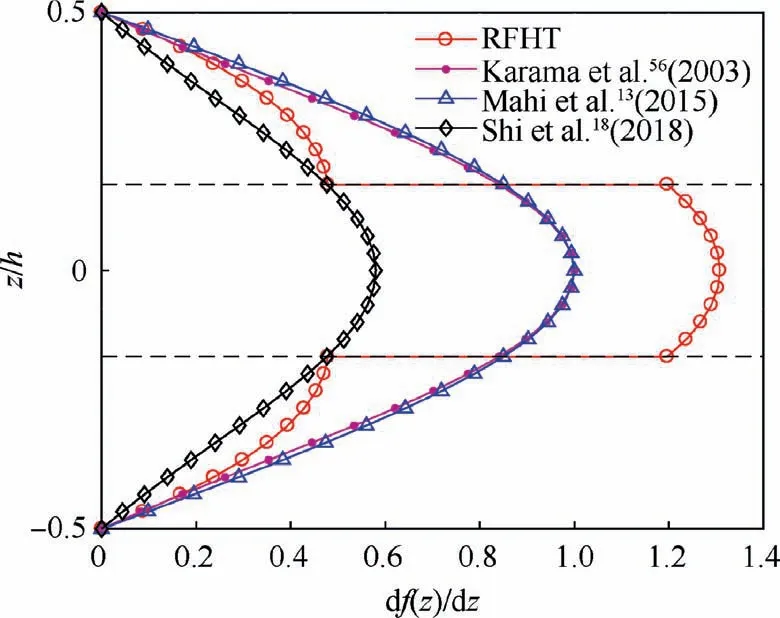
Fig. 3 Derivatives of shear deformation functions relative to coordinate z through thickness of plate.



4. Numerical examples
In this section, the free vibration analysis of simply-supported composite and sandwich plates will be investigated by the RFHT in conjunction with other models. Firstly, the results calculated from the RFHT and results obtained from other models of a layered composite plate are verified by the 3D elasticity solutions,which can demonstrate the performance of the RFHT and the listed models. Subsequently, results of sandwich plates obtained from the selected models are compared to the 3D FEM results, which can assess capability of various five-unknown models.
4.1. Example 1
In this section,free vibration of a laminated composite square plate (a=b) with simply-supported boundary condition is analyzed.


Table 2 Comparison of fundamental frequencies obtained from various models for a four-layer [0°/90°/90°/0°] plate (a/h=5).

Table 3 ck1, ck2, dk1 and dk2 for Example 1.

Effects of material constants on first natural frequencies obtained from various models for a four-layer plate are shown in Table 2.What can be noted is that natural frequencies gradually increase with increase of the Eto Eratios. Moreover,numerical results indicate that the error between the results calculated from the RFHT and the exact solution is very small.The maximum percentage error of the RFHT for different modulus ratios is less than 2%. Besides the exact elasticity solutions,the results obtained from other higher-order theories are also chosen for comparison.One can notice that compared with the exact elasticity solutions, all of the listed models perform well.
In addition,values of c,c,dand din Eq.(5)have been presented in Table 3. Furthermore, f(z)and its derivative with respect to z,namely f´(z)are given in Table 4.It requires to be shown that values in Tables 3 and 4 retain the same for different Eto Eratios. These values can be utilized to verify thecontinuity conditions of transverse shear stresses at interfaces and the zero transverse shear stresses on the surfaces.

Table 4 f(z) and f´(z) for Example 1 (h=1).
4.2. Example 2
In this section, free vibration of the sandwich square plate(a=b)with simply-supported boundary conditions is studied.
In this case,material properties at each ply are presented by(A)face sheet(aluminum):tensile modulus E=71 GPa,Poisson’s ratio ν=0.3, density ρ=2700 kg/m; core (polymethacrylimide foam): tensile modulus E=92 MPa,Poisson’s ratio ν=0.375, density ρ=75 kg/m.

Fig. 4 Convergence rate of three-dimensional finite element(tc/tf=8, a/h=100).

Table 5 Comparison of natural frequencies obtained from various models for a three-layer sandwich plate (tc/tf=8, a/h=100).
The normalized natural frequencies can be determined by ω=ωa(ρ/E)/h; tand trepresent the thickness of the core and the face sheet, respectively. It needs to be indicated that it is hard to find exact 3D elasticity solutions of free vibration of such sandwich plate.Therefore,the 3D-FEM(C3D8R)results of ABAQUS will be chosen to evaluate the performance of various models. Firstly, four mesh configurations including 1.00×10, 1.96×10, 4.00×10and 9.00×10meshes respectively are utilized to study converged performance of 3D-FEM. In Fig. 4, it can be noticed that results obtained from 4.00×10meshes are close well to those obtained from 5.00×10meshes, so that mesh configuration including 4.00×10meshes will be utilized to produce 3D-FEM results in following computation.
The first six natural frequencies corresponding to displacement parameters wof thin sandwich plate (a/h=100) are listed in Table 5, which contains the results calculated from RFHT and those obtained from the 3D-FEM, the thirdorder model proposed by Reddy,the sinusoidal model proposed by Touratierand the hyperbolic sine model proposed by Soldatos.In addition, the recent models proposed by Singh and Singh,Shi et al.,Kumar et al.and Shukla et al.are also chosen for investigation and comparison. By comparing to the 3D-FEM results, it can be observed that all models listed in Table 5 can perform excellently to predict the fundamental frequencies.For the higher-order frequencies,the present model RFHT can still yield accurate results of sandwich plates, as the maximum percentage errors for a three-layer sandwich plate (t/t=8, a/h=100) are still less than 2%. In addition, the percentage errors of several models relative to the 3D-FEM results are shown in Fig. 5. However,for the higher-order frequencies obtained from other models,the maximum percentage errors are even more than 50%.

Fig.5 Comparison of natural frequencies obtained from various models (tc/tf=8, a/h=100).

Table 6 Comparison of natural frequencies obtained from various models for a three-layer sandwich plate (tc/tf=8, a/h=20).

Fig.6 Comparison of natural frequencies obtained from various models (tc/tf=8, a/h=20).
In order to assess effect of plate thickness on dynamic behavior, natural frequencies obtained from various models with three-layer moderately thick sandwich plate (a/h=20)have been compared in Table 6. The results of the model RFHT gradually deviate from the 3D-FEM results with increase of order number of natural frequencies,and the maximum percentage error of RFHT reaches at 11.64%.Differing from thin sandwich plate, it’s even a strenuous work to yield accurately the first natural frequencies of sandwich plate for the rest of the listed models,as the maximum percentage errors of these models are more than 100%, which have been depicted in Fig. 6. Subsequently, natural frequencies of thick sandwich plate (a/h=4) are presented in Table 7. It can be observed that the first three natural frequencies of RFHT are compared well with the 3D-FEM results. These results are a clear demonstration that the length-to-thickness ratios have an important impact on capability predicting the higherorder natural frequencies of the five-unknown higher-order theories.

In addition, effect of the t-to-tratios on natural frequencies is firstly investigated, which is shown in Table 10. For the first natural frequency of the sandwich plate (t/t=5),the percentage error of the model RFHT is 1.33%. Subsequently, the capability of various five-unknown models predicting higher-order frequencies will be assessed in detail.Percentage errors of the chosen higher-order models relative to the 3D-FEM results in Table 10 have been depicted in Fig.7,which indicated that percentage errors of various models have a trend of gradual increase for the higher-order natural frequencies.

In order to study effect of the thickness/length ratios on natural frequencies,natural frequencies of thick and thin sandwich plates have been presented in Table 13 by using 3D-FEM,S4R, RFHT and the higher-order models of Shi et al.and Shukla et al.It needs to be shown that S4R is a 4-node double curved thin or thick shell element in ABAQUS using the reduced integration. Numerical results show that S4R obviously underestimate the higher-order frequencies of thick plate(the thickness/length ratio is 1/4). Nevertheless, the higherorder models proposed by Shi et al.and Shukla et al.largely overestimate the natural frequencies. As the thickness/length ratio is reduced to 1/100,results of S4R are nearly equal to those of 3D-FEM and RFHT. For thick and thin plates, it can be seen that results of RFHT are in good agreement with 3D-FEM results.


Table 7 Comparison of natural frequencies obtained from various models for a three-layer sandwich plate (tc/tf=8, a/h=4).

Table 8 ck1, ck2, dk1 and dk2 for Example 2 (tc/tf=8).

Table 9 f (z) and f´(z) for Example 2 (tc/tf=8, h=1).



Table 10 Comparison of natural frequencies obtained from various models for a three-layer sandwich plate (tc/tf=5, a/h=100).

Fig.7 Comparison of natural frequencies obtained from various models (tc/tf=5, a/h=100).

Table 11 , , and for Example 2 (tc/tf=5).

Table 12 f (z) and f´(z) for Example 2 (tc/tf=5, h=1).

Table 13 Effect of the thickness/length ratios on natural frequencies of the three-layer sandwich plates (tc/tf=8).

Fig. 8 Comparison of displacement and stresses obtained from various models (tc/tf=8, a/h=100).

5. Conclusions
In present work, a refined higher-order theory is developed for free vibration analysis of layered composite and sandwich plates. The developed model can meet the interlaminar continuity conditions and the free-surface conditions of transverse shear stresses. Moreover, only five unknowns are included in the proposed model, which is the same as those of other five-known higher-order models. For the sake of assessing the performance of the five-unknown higher-order models, free vibration analysis of the composite and sandwich plates was carried out by applying the analytical approach. Results obtained from the proposed model have been compared to the 3D elasticity solution,the 3D finite element results and those obtained from the chosen five-unknown higher-order models. By means of numerical analysis and discussion, the following conclusions have been drawn:
(1) For layered composite plate, all of the models perform well for the first natural frequency. For thin sandwich plate, the chosen five-unknown models violating interlaminar continuity are unable to yield accurately the higher-order natural frequencies.
(2) For moderately thick and thick sandwich plates,the present model has attained good performance in spite of the fact that the higher-order frequencies are slightly more than 3D-FEM results.Nevertheless,the proposed model is more efficient in comparison with the 3D-FEM method.In addition,the t-to-tratios of sandwich plate have also an impact on prediction of natural frequencies.
(3) If the models lose capability to yield correctly the displacement and stresses, they will also encounter difficulty to predict correctly natural frequencies of the sandwich plates.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Fig. 9 Comparison of displacement and stresses obtained from various models (tc/tf=8, a/h=20).
Acknowledgements
The work was supported by SKLLIM1902 and the National Natural Sciences Foundation of China (No. 11402152).
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Optimal trajectory and downlink power control for multi-type UAV aerial base stations
- Effects of flow parameters on thermal performance of an inner-liner anti-icing system with jets impingement heat transfer
- Effects of wing flexibility on aerodynamic performance of an aircraft model
- Aerodynamic performance enhancement of co-flow jet airfoil with simple high-lift device
- Adaptive fuzzy terminal sliding mode control for the free-floating space manipulator with free-swinging joint failure
- Influence of longitudinal-torsional ultrasonicassisted vibration on micro-hole drilling Ti-6Al-4V
