Optimal trajectory and downlink power control for multi-type UAV aerial base stations
2021-10-27LixinLIYnSUNQinqinCHENGDweiWANGWenshengLINWeiCHEN
Lixin LI, Yn SUN, Qinqin CHENG, Dwei WANG, Wensheng LIN,Wei CHEN
a School of Electronics and Information Engineering, Northwestern Polytechnical University, Xi’an 710129, China
b Department of Electronic Engineering, Tsinghua University, Beijing 100084, China
KEYWORDS Mean-Field-Type Game(MFTG);Power control;Q-learning;Trajectory;Unmanned Aerial Vehicle(UAV)
Abstract Unmanned Aerial Vehicles (UAVs) enabled Aerial Base Stations (UABSs) have been studied widely in future communications.However,there are a series of challenges such as interference management, trajectory design and resource allocation in the scenarios of multi-UAV networks. Besides, different performances among UABSs increase complexity and bring many challenges.In this paper,the joint downlink transmission power control and trajectory design problem in multi-type UABSs communication network is investigated. In order to satisfy the signal to interference plus noise power ratio of users, each UABS needs to adjust its position and transmission power. Based on the interactions among multiple communication links, a non-cooperative Mean-Field-Type Game (MFTG) is proposed to model the joint optimization problem. Then, a Nash equilibrium solution is solved by two steps: first, the users in the given area are clustered to get the initial deployment of the UABSs; second, the Mean-Field Q (MFQ)-learning algorithm is proposed to solve the discrete MFTG problem. Finally, the effectiveness of the approach is verified through the simulations, which simplifies the solution process and effectively reduces the energy consumption of each UABS.
1. Introduction
With the great development of control, computers and communications, Unmanned Aerial Vehicles (UAVs) have been widely used in commercial, agricultural, and industrial industries, such as disaster relief, power inspection, express transportation, etc.Specifically, in communication scenarios,there are two main roles that UAVs play: UAV Aerial Base Stations (UABSs) and the aerial users.Because of the improvement of loading capacity of UAV and the miniaturization of communication equipment, UABS has been widely studied in recent years.Compared with the ground fixed base stations, UABSs can reduce the communication pressure and satisfy the communication requirements of the ground users as much as possible.Compared with in-vehicle communication, the UABS with the Line-Of-Sight (LoS) communication link has better communication channel and wider coverage.In addition, UABS has low communication overhead, where the replacement of communication equipment is faster and cheaper.Therefore, UABS is a promising wireless communication technology for dynamic and diversified future communication networks.
In the early researches,a single UAV was used as a static or mobile aerial base station to optimize the altitude of the UAV to improve the maximum system sum-rate and coverage probability.A mobile UAV employed as a full-duplex relay that assists the communication link between separated nodes without direct link was investigated. An efficient spectrum sharing method for UAV and D2D communications is designed by optimizing the transmission power and trajectory alternately. However, with the rapidly increasing demand of wireless services, single UABS often fails to satisfy the needs of complicated scenarios in large-scale applications.To address this issue, it is necessary to form a multi-UABS network to improve communication efficiency.
However,there are still many challenges in the multi-UABS communication network. There are three main challenges. (A) Interference management problem: the spectrum shares among UABSs when they communicate with users because of the limited spectrum resources,which causes serious interferences; (B) Trajectory planning problem: Three-Dimensional(3D) trajectory control is more complicated than Two-Dimensional(2D),which causes great challenges,such as higher computational complexity;(C)Network topology problem: the topology of the whole network changes dramatically because of the high mobility of UABSs,which directly changes the interferences and interactions.Besides, the communication energy consumption, flight energy consumption, deployment location and Quality of Service (QoS) of UABSs also affect the stability and efficiency of communication in multiple UABS networks.
Moreover, the UABS should quickly adjust its position according to the ground user request, which will cause the changing topology of the multi-UABS network.Then,the communication resources of the UABSs including trajectory planning and interference management need to be re-planned. In addition, considering the performance differences among UABSs in practical applications,the multiple UABSs communication networks are actually made up of many different types of UABSs.The diversity of UABSs leads to the complex multitype UABS network, which is embodied in service radius,energy storage,and so on.Therefore,joint optimization of trajectory and transmission power has important practical significance in the multi-type UABS communication networks.
In recent years,game theory has been proven to be an effective tool for studying effective distributed strategies and optimal control strategies.Specifically, the trajectory design and downlink transmission power control problem of multitype UABSs can be expressed as a game process.In this game,each UABS minimizes its cost function through optimizing flight control strategy and power control strategy. Moreover,the selfish behavior of any party will affect the cost of other communication links. Therefore, the control strategy of each UABS is subject to other individual strategies involved in the multi-type UABSs communication network.
However, traditional games must simulate the interactions of each agent, which will cause a complex high-dimensional problem when a large number of agents are involved.Hence,the interactions of every agent are averaged as the interaction of the mass by introducing the concept of‘‘mean field”,which means that we just need to consider the interaction between a single agent and the collective behavior of the other agents.This leads to a relatively new game theory, Mean-Field Game(MFG), which simplifies the interactions of the mass by a mean field term to reduce the complexity of interactions significantly.Up to now, MFG has many applications in communications, including UABSs’ deployment, delay optimization in edge caching and interference management.However,in the MFG theory,the following assumptions must be established: (A) large-scale: the number of participating game agents tends to be infinite or continuous; (B) anonymity/homogeneity: the attributes of decision-makers should be homogeneous;(C)non-atomic:the strategy of a single agent is negligible for global utility. The establishment of these assumptions can simplify the problem, but make the research model far from the practical applications.
In order to relax the limitations of MFG,a more flexible game framework Mean-Field-Type Game (MFTG) emerged.In MFTG, the following assumptions are formulated: (A)the influence of a single agent on the mean term is fully considered;(B)the number of agents is arbitrary;(C)the agent is not required to be indistinguishable.There have been many researches on the application of MFTG in engineering. In practice,the number of UABSs is limited, and the homogeneity of each UABS cannot be guaranteed. Therefore, the MFTG model is more suitable for the optimization of trajectory and transmission power in the multi-type UABSs communication networks.
On the other hand,employing Reinforcement Learning(RL)into communication and network is being widely studied in the next generation(6G)networks.To solve the problem of trajectory and power optimization in the multi-type UABS communication networks, we first divide the service area into clusters according to the user density by usingK-means method,and each UABS is deployed in each cluster center initially. Then, according to the user service request within the cluster, the flight trajectory and downlink transmission power of each UABS are jointly optimized.It is modeled as a MFTG problem,which is solved by the Mean-Field Q(MFQ)-learning algorithm.The main contributions of this paper are as follows:
(1) The communication model with multi-type UABSs: the multi-type UABSs in the air-to-ground communication network are investigated, which have different service capabilities (energy storage, flight speed and Signal to Interference plus Noise power Ratio (SINR)threshold).
(2) The MFTG framework of the communication network:the state dynamic equation and cost function of each UABS are derived,which are in line with practical applications. The jointly power and trajectory optimization of UABSs as a MFTG is proposed, in which each UAV minimizes its own cost function subject to the state dynamic of the networks.
(3) The solution for the discrete MFTG model: the discrete time MFTG is formulated to simplify the problem.Based on the discrete MFTG model, we propose a two-step approach to solve the joint optimization problem. (A) By invoking the K-means algorithm, the cell partition according to the density of user distribution is obtained, which can determine the initial deployment of the UABSs.; (B) The MFQ-learning based deployment algorithm is designed to explore the optimal downlink transmission power and trajectory.
(4) The simulation results: simulation results demonstrate the performance of the strategies and energy consumption curves of multi-type UABSs solved by MFQlearning approach, which can efficiently reduce the cost of each UABS.
The rest of the paper is organized as follows. The system model for the air-to-ground communication network with multi-type UABSs is presented in Section 2. The trajectory planning and downlink power control problem is formulated and analyzed using MFTG in Section 3. In Section 4, the MFTG is discretized and solved by the MFQ-learning algorithm.Simulation and analysis results of the optimal strategies are presented in Section 5. Section 6 draws the conclusions.
2. System model
In this section,we introduce the system model.The multi-type UABSs communication scenario model is given in Subsection 2.1. In addition, in Subsections 2.2 and 2.3, the network dynamic equation and the cost function are designed based on the communication scenario.
2.1. Communication scenario
As shown in Fig.1,the multi-type UABSs communication network is utilized in this paper,where UABSs have different service capabilities (energy storage, flight speed and SINR threshold). In the emergency communication scenario or the hotspot service scenario, multiple UABSs are deployed to satisfy user service requests. In the hotspot scenario, when users request service, UABSs deliver hot contents such as video to users through the LoS link. Firstly, for simple analysis, we assume that the location information of ground users in the service area is known. The initial deployment locations of UABSs through centralized control center by K-means algorithm are obtained. The Ground Control Station (GCS)obtains the operating state of the drone and the navigation interaction information among the UAVs through the Control and Non-Payload Communication(CNPC)link.It is assumed that each UABS knows the location information of all users in the served area. During the process of flight, multiple UABSs communicate location and transmission power information through a fixed frequency with each other.Due to limited spectrum resources, multiple UABSs need to use the same frequency band for terrestrial communication services when serving multiple users in the given area. However, it causes mutual interference among UABSs, which seriously affects the communication quality. Therefore, each UABS needs to adjust the position and the downlink transmission power to suppress interference and satisfy the communication quality of the user. However, the adjustment of the UAV’s position will change the air-to-ground communication channel, which in turn affects the transmission power of the UABS.Therefore,joint optimization of location and downlink transmission power has important practical significance.
Specifically, we consider the multi-type UABSs communication system composed of a limited number of different types of UABSs and multiple users,where the different types refer to the difference of UABS in power reserve, flight propulsion power and service radius.In this model,we consider deploying M(M ≥2) UABSs in the given area Z, and each UABS i,(i ∈{1,2,...,M}) serves multiple users in the circular area.At the initial moment, M UABSs and U users are distributed independently and randomly in the region,as shown in Fig.1.
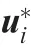
2.2. Network dynamic equation

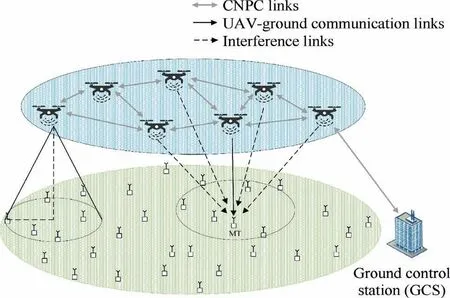
Fig.1 Multi-type UABSs serve a large number of users within a given area.

2.3. Design of cost function
At any time t,multiple UABSs communicate with users in the cluster.Due to spectrum sharing among UAVs,it causes interference in the communication process to the ground.The communication process of UABS consumes energy, and the flight process requires energy.Therefore,the cost function of UABSs includes communication cost and flight cost.
Given the total flight cost cof UABS i as a function of the relevant flight distance, we define the flight propulsion power parameters for the unit square flight distance of UABS i.Then the flight energy consumption of the UAV can be expressed as

where d=‖q(t)-l(t)‖,d=‖q(t)-l(t)‖represents the distance between UABS i and UABS j to user k, and l(t) represents the user’s position. P(t) is the transmission power of UABS i at time t, gis the channel gain of UABS i to user k, and α represents the trajectory fading factor.

In summary, the terminal cost function of UABS i only depends on the final state of communication network x(T).
By analyzing cost function and state dynamic equation,it is easy to find that UABSs with different performances have different cost functions.Therefore,according to the above formulas, the trajectory and power optimization problem of multitype UABSs will be modeled as MFTG in the next section.
3. Mean-field-type game formulation
MFG has been widely used in multi-agent scenarios. The main idea of the MFG is based on aggregated information about the state of other decision makers.Each decision maker determines its optimal strategy to optimize its cost function, subject to the state dynamic equation. However, since the MFG must be used with assumptions that deviate from actual engineering applications,a game model MFTG that relaxes MFG conditions was proposed in Ref.Specifically, MFTG has the following advantages in model construction: (A) the number of agents is limited or infinite;(B)the influence of a single agent on the mean field term and global effect is considered;(C)the agents do not need to guarantee the same property.These assumptions make the MFTG model more suitable for practical scenarios.
In this paper, we regard communication links between the UABSs and ground users as individuals participating in MFTG. The control (transmission power and position adjustment)of each UABS affects the communication quality of the users.Therefore, the selfish behavior of either party will affect the cost of others. The control strategy of each UABS is subject to other individuals’ strategies involved in the game, and the evolution of the system state is determined by the control strategy of all UABSs.
We consider two aspects of heterogeneity among individual agents,the flight propulsion power of the UABSs and the user communication requirements SINR, which conform to the condition of the MFTG. Thus, we will formulate a MFTG to model the joint optimization problem of trajectory and transmission power in multi-type UABSs network in Subsection 3.3.Specifically,the state dynamic equation and cost function are reconstructed in Subsection 3.1 and 3.2, which introduce the mean field term to represent the interferences from the other UABSs.
3.1. State dynamic equation with mean field terms
Because the state and control strategy of each agent is affected by other agents, we introduce the mean field terms to substitute the influence from others. For UABS i, the state dynamic equation can be rewritten as
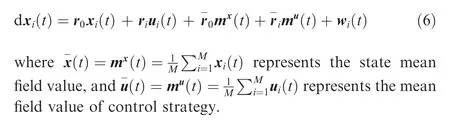
3.2. Cost function with mean field terms
In this model, the mean field terms x(t) and u(t) affect the UABS’s running cost function and the terminal cost function.Thus, the operating cost of the UABS i can be remodeled as
3.3. Non-cooperative MFTG problem
Considering a communication network consisting of M ≥2 multi-type UABSs,each of them can communicate with terrestrial users in the given service area. In addition, each UABS can obtain the optimal flight strategy and transmission power strategy by minimizing its own cost function in the noncooperative game scenario.Thus,the problem can be modeled as the following MFTG problem:
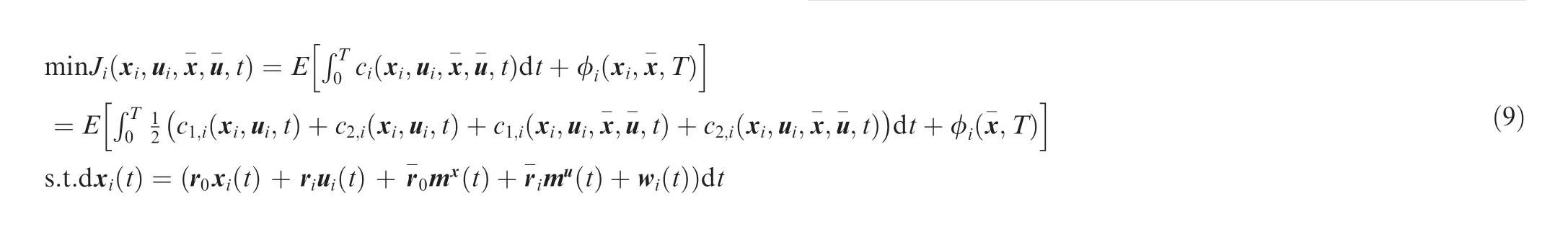
Therefore, any control strategy u(t) satisfies Eq. (9) as the optimal response of UABS i.According to the above formulas,the solution of the MFTG problem will be solved in the next section.
4. Mean-field-type game solution
In this section,the MFTG problem is discretized firstly in Subsection 4.1 Then, the equilibrium solution of this problem is obtained by using K-means algorithm and MFQ-learning algorithm in Subsection 4.2.
4.1. Discretize mean-field-type game
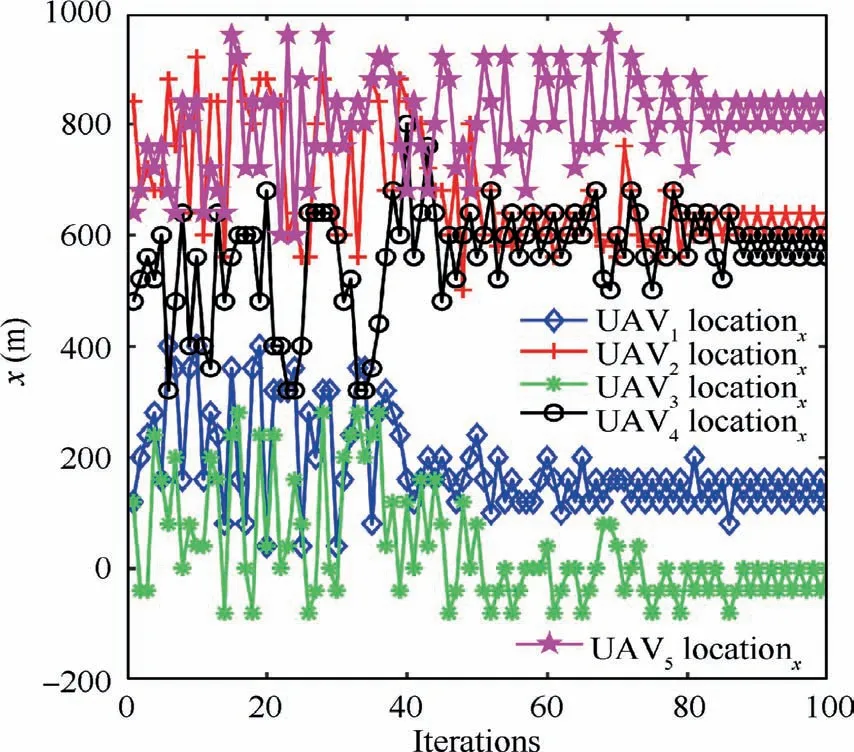
In the framework of problem (9),time space 0 where^cdepends on the measure m(t,. )and the strategy profile u(t).Similarly,one can rewrite the expected value of the terminal cost as As shown in cost function (10), the best-response strategy probably depends on the state mean field term m, which is referred to as feedback strategy. Therefore, m(t) can be expressed as a function of (x(t),m(t,·)). Thus, the payoff^c(t,·) can be written as a function of (m(t,·),x(t)). In this case, the system has continuous state space. This paper considers the interactive state dynamic in discrete time as In this paper, we need to solve the Markov problem in Eq. (15) when a large number of agents exist simultaneously.In this communication network, multiple agents directly interact with a limited number of other agents. Based on the construction of the discrete MFTG problem in Eq.(15), we can use the Multi-Agent Reinforcement Learning(MARL) to solve the optimal control strategy to jointly optimize the trajectory and downlink power of multi-type UABSs. The extensibility solution of this problem is obtained by simplifying the interactions within the agents to the mean term. The main idea of MARL is to reinforce each other between two agents rather than multiple agents: the optimal control strategy of a single agent is based on the dynamic of the network, and the state of the network is updated according to the individual strategy. On this basis, the MFQ-learning algorithm is applied to solve the optimal control problem. Algorithm 1 K-means algorithm for initial deployment of UABSs 1. Input:2. N users location coordinates: D= l1,l2,...,lN{ },li =[xi,yi];Cluster number: k.3. Output:4. Cell Partition of Ground Users C = C1,C2,...,Ck{}5. Repeat:6. Calculate the class that each user should belong to:7. for i=1,2,...,N do 8. c(i) :=argmin j‖l(i)-μj ‖2 9. Recalculate the center of mass of the class j:10. for j=1,2,...,k do 11. μj :=∑N i=11 {c(i)=j}l(i)∑N i=11 {c(i)=j}12. end for 13. end for In this subsection, the steps of the solution in detail as shown in Fig. 2 are presented. In an emergency communication scenario or hotspot area, the service requests of users are roughly proportional to the user density. Based on this,we firstly cluster users according to the density based on the K-means algorithm, and initially deploy the UABSs in the center of each cluster to ensure the full coverage of the given service area. Due to the limitation of spectrum resources, the UABSs adopt TDMA to communicate with users. Then, in time slot t, the UABS should adjust the position and transmission power according to the user’s service request to ensure successful communication. Thus, the optimization problem is simplified to a region segmentation problem, which is formulated as Fig. 2 Procedure for solving problem of optimizing downlink power and trajectory design of multiple UABSs. The steps to solve this problem are described in detail in the following subsection. 4.2.1.Step 1.Initial algorithm for cell partitions of ground users It is assumed that N users are randomly distributed in the specified region. We have known the location information of all users, and determine to deploy M UABSs to serve the ground users.The first step is to obtain the initial deployment of multitype UABSs, which is to obtain the central locations of the users’ clusters. In each cluster, the users are linked with a UABS.K-means algorithm can solve the problem of clustering and obtain the initial 3D position of the UABSs with a low complexity.This algorithm is capable of partitioning users into different clusters based on the policy of nearest neighbor barycenter, and recalculates the barycenter of each cluster.Specifically,the K-means algorithm obtains the results that the squared error between the empirical mean of a cluster and the points is minimized. By invoking the K-means algorithm which is summarized in Algorithm 1, the users are partitioned into clusters to obtain the initial deployment of UABSs. 4.2.2. Step 2. MFQ-learning algorithm for optimizing downlink power and trajectory of multiple UABSs Algorithm 2 Mean-Field Q (MFQ)-learning algorithm for optimizing downlink power and trajectory of multiple UABSs jointly.1. Initialization:2. Initial position of UAVs and users derived by K-means algorithm.3. Initial Qi table and Ri of each UABS, i ∈{1,2,...,M}.4. Process:5. Deploy UABSs at the initial positions.6. The downlink transmission power of UABS i is Pi =Pmax Ni .7. Repeat:8. Select the action a={a1,a2,...,aM} to obtain max Qi according to the ε-greedy policy.9. For each UABS, compute the new mean action mai = 1 Ni∑ak,ak ~J(·|s,ma-k).10. Take action a, observe the next state s′ ={s1,s2,...,sM}and reward Ri(si,ai).11. Update the Qi table according to Eq. (16).12. Output:13. The trajectory and downlink transmission power of UABSs. In this section, the basic simulation parameter setting is introduced in Table 1 in Subsection 5.1. Then, the optimal strategies are simulated and analyzed in Subsection 5.2. At present,there are few researches on joint trajectory and downlink power optimization in multi-type UABSs network.Moreover, the SINR and cost curves are given to evaluate the performance of the proposed MFQ-learning algorithm in Subsection 5.3. It is assumed that there are N=100 users randomly distributed in the designated area that M=5 UABSs need to serve at the initial time, as shown in Fig. 3. The specified area of the rectangle consists of X axis range[0,1000]m and Y axis range [0, 1000] m. In this model, it assumes that the flight height of all UAVs remains unchanged h=500 m, and only the horizontal 2D position of the UABSs is planned to simplify the problem. According to the initial distribution of users in Fig. 3, we firstly cluster users based on the K-means algorithm to obtain the user cluster diagram as shown in Fig. 4. On this basis,according to the number of users in the cluster and the service radius when the height of the UABSs is h=500 m, UABSs are reasonably deployed in the center of each cluster. At the same flight height,UABS with a large service radius and largeenergy storage is deployed in cluster center with a large number of users and small concentration. Table 1 Parameters in numerical simulation. Fig.3 Two-dimensional distribution of 100 users at initial time. Fig. 4 Clusters of 100 users based on K-means algorithm. Due to the limited spectrum resources, the UABSs adopt TDMA to communicate with users. After reasonably deploying UABSs, the task space V={v(x,y,τ)|(x,y)∈Z,i ∈(1,2,...M)} according to the service requests of users is obtained in the same time slot. In this paper, users requesting services in five clusters are randomly selected to constitute the total task space V. As shown in Fig. 5, the initial distribution of the UABSs based on the K-means algorithm and the location map of the users requesting service are presented. Then,the flight trajectory and downlink power of multiple UABSs will be optimized according to the total communication mission space. In order to show the evolution of strategy by the MFQlearning algorithm in time t ∈[0,T], the trajectory planning diagram in Fig. 6 and the transmission power in Fig. 7 are shown. In this simulation, we set T=10 steps. Fig. 6 shows the trajectory planning of multiple UABSs based on the MFQ-learning algorithm. During this time interval, it is obvious that the number of moves of UABS 1 flies five steps at most, and it finally reaches the small area of the user requesting service,where UABS approximately reaches the designated service position. UABS 5 has the smallest mobile steps, and only moves 3 steps to reach the designated user service position in the cluster. Meanwhile, UABSs 2 and 3 only move four steps in the interval, and neither of them reach the designated user position in the cluster.Fig.6 fully shows that the equilibrium solution exists in the MFTG problem model. When all the UABSs make decisions, they interact with each other for information, and finally get the stable equilibrium solution.All UABSs found the best position for communication within the time interval. Fig. 5 Distribution of UABSs and users requesting service based on K-means algorithm. Fig. 6 Optimal trajectory of multiple UABSs based on MFQlearning algorithm. Fig. 7 Downlink transmission power of multiple UABSs based on MFQ-learning algorithm. In order to characterize the communication quality of users in this planning process, the SINR of users is analyzed. As shown in Fig. 8, the SINR of all users eventually exceeds the threshold and remains stable. Users 5 and 4 start off with SINR well above the threshold and drop down to near the threshold. Although a high SINR can guarantee the normal communication of users, it also causes the waste of communication energy, i.e., the communication cost becomes higher.Therefore,reducing the SINR to the threshold can ensure normal communication and avoid wasting communication resources so as to reduce communication costs. The SINR trend of all users in Fig. 8 shows the significance of the MFQ-learning algorithm. In this subsection, the energy consumption generated by the above multi-type UABSs strategies is analyzed, E(t) (J) is compared with different decision-making schemes. First, we define the total energy consumption of UABS i as the sum of flight energy consumption and communication energy consumption, which is given as where E(W/m)is the propulsion power per square distance,‖q(j)‖(m) is the flight square distance of j step, and p(j)(W) is the transmission power. Fig. 8 SINR of multiple UABSs based on MFQ-learning algorithm. Fig. 9 Comparison of energy consumption among different UABSs based on MFQ. Fig. 9 shows the total energy consumption curve under the joint optimal trajectory and power strategies generated by the UABSs based on the MFQ-learning algorithm. Taking UABS 5 as an example, the slope of the total energy consumption curve changes significantly at the time t=3. In combination with trajectory planning (Fig. 9), it can be seen that after t=3, the position of the UAV no longer changes, i.e., the flight energy consumption is 0. Therefore, the slope of energy consumption curve of UABS 5 decreases obviously.Compared with UABS 1, the transmission power is significantly lower than UABS 5 due to the difference in the energy carried by itself.Therefore,the communication energy consumption after it reaches the designated service position has no obvious impact on the total energy consumption, and the slope of energy consumption curve is nearly 0. The optimal transmission power strategy based on MFQlearning algorithm is compared in Fig. 10. The comparison curve of total energy consumption generated by direct flight to the designated service location and trajectory planning of the MFQ-learning algorithm is shown in Fig. 10. As can be seen from the curve, the total energy consumption of UABSs 3,4 and 5 using the optimized trajectory decrease significantly,while the energy consumption of UABSs 1 and 2 increase. In the direct flight trajectory to the top of the user requesting service,the communication cost caused by interference is not considered,so even if the total energy consumption of the UABSs 1 and 2 can be reduced,the normal communication of the user cannot be guaranteed in the flight process, which can increase the communication cost. In order to analyze the convergence of the MFQ-learning algorithm, Fig. 12 shows the changes in the X axis of all UABSs trajectories with the number of iterations. It can be clearly seen from Fig. 12 that the MFQ-learning algorithm can converge to the equilibrium solution with a small number of iterations,which proves the practicality and convergence of the MFQ-learning algorithm. Fig. 10 Comparison of energy consumption under different trajectory planning. Fig. 11 Comparison of energy consumption under different downlink transmission power. Fig. 12 Convergence of MFQ-learning algorithm. In this paper, the joint trajectory planning and transmission power control problem of multi-type UABSs in emergency communication scenes or hotspots is investigated. In this model, each UABS planed the flight trajectory and transmission power, so as to minimize the cost of the UABS under the condition of guaranteeing the user’s SINR threshold.According to the performance differences among UABSs (stored energy, flight propulsion power, etc.), we constructed the model as a MFTG problem. Based on this framework,the state dynamic equation and cost function of the whole communication system were designed. The two-step approach is proposed to solve the joint optimization problem. First, the initial deployment of the UABSs is obtained by invoking the K-means algorithm according to the density of user distribution. Second, the Nash equilibrium solution is explored by the MFQ-learning algorithm. Simulation results show that the Nash equilibrium solution of the MFTG exists. The joint optimal trajectory and transmission power of each UABS are obtained to minimize the cost function. In addition, compared with the average transmission power strategy, the Nash equilibrium solution can guarantee the SINR threshold of users when the total energy consumption is similar, which proves the effectiveness of the MFQ-learning algorithm. Declaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Acknowledgements This work was co-supported by the National Natural Science Foundation of China (Nos. 62001387, 61901379), the Natural Science Basic Research Plan in Shaanxi Province(No.2019JQ-253), the Key R&D Plan of Shaanxi Province (No. 2020GY-034),the Aerospace Science and Technology Innovation Fund of China Aerospace Science and Technology Corporation,the Shanghai Aerospace Science and Technology Innovation Fund(No. SAST2018045), the China Fundamental Research Fund for the Central Universities (No. 3102018QD096), and the Seed Foundation of Innovation and Creation for Graduate Students in Northwestern Polytechnical University (No.CX2020152). This paper was presented in part at the 2020 IEEE International Conference on Communications (ICC).
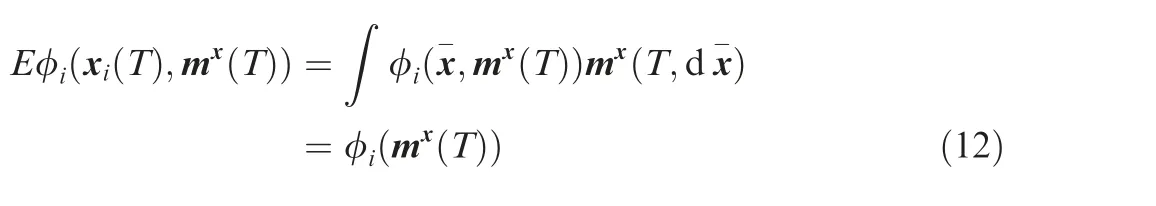



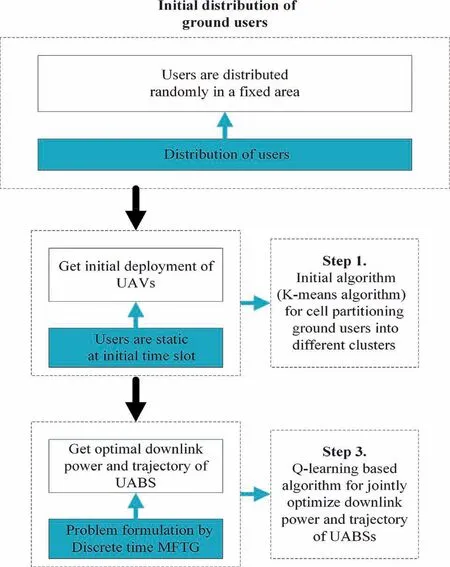
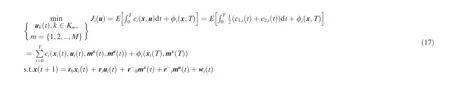
4.2. Procedure of solution






5. Numerical results
5.1. Basic simulation setting
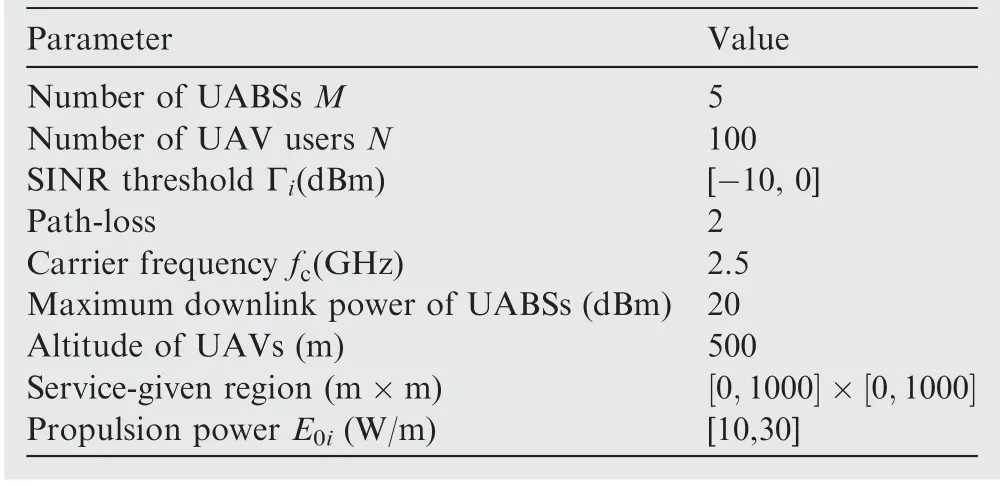

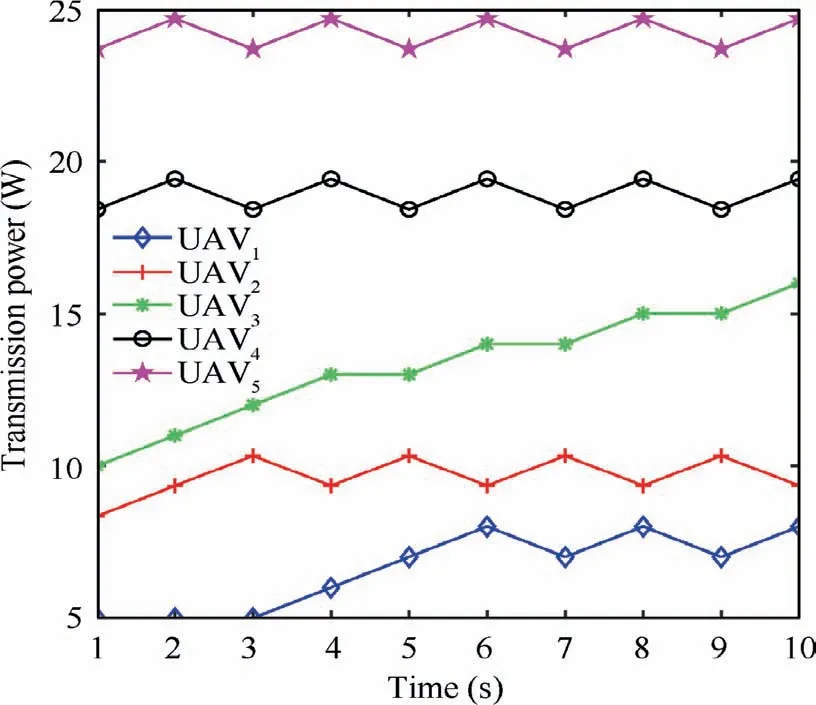
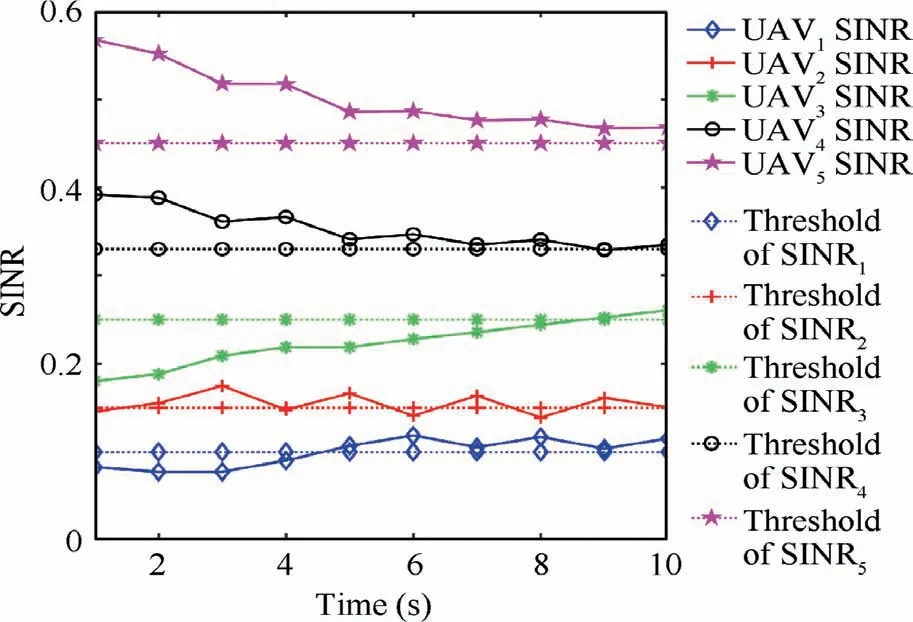
5.2. Joint optimization of downlink transmission power and trajectory simulation results of multi-type UABSs




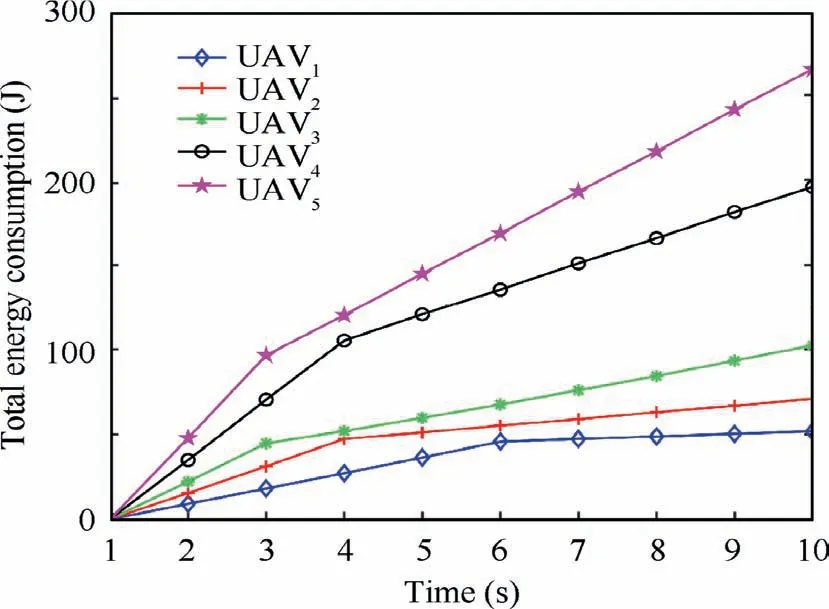
5.3. Energy consumption performance


6. Conclusions


杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Effects of flow parameters on thermal performance of an inner-liner anti-icing system with jets impingement heat transfer
- Effects of wing flexibility on aerodynamic performance of an aircraft model
- Aerodynamic performance enhancement of co-flow jet airfoil with simple high-lift device
- Adaptive fuzzy terminal sliding mode control for the free-floating space manipulator with free-swinging joint failure
- Influence of longitudinal-torsional ultrasonicassisted vibration on micro-hole drilling Ti-6Al-4V
- Response and stabilization of a two-stage axial flow compressor restricted by rotating inlet distortion
