群智感知环境中基于GRU网络的用户位置预测模型 *

张安冉，廖祎玮，赵国生，王 健

(1.哈尔滨师范大学计算机科学与信息工程学院,黑龙江 哈尔滨 150025;2.哈尔滨理工大学计算机科学与技术学院,黑龙江 哈尔滨 150080)

1 引言

移动群智感知MCS(Mobile Crowd Sensing)是在参与感知和众包等概念的基础上发展而来的，刘云浩教授在2012年率先提出群智感知计算的概念[1]。MCS作为一种大规模获取数据的全新感知模式，已经应用于解决包括街边停车管理[2]、交通状况检测[3]和环境污染监测[4]等多种问题。但是，在用户分布稀疏的情况下进行任务分配时，可能会出现任务所在区域的用户数量覆盖不足的问题，导致不能有效进行感知任务的分配。因此，用户未来时刻位置的预测对于群智感知应用极其重要。若能对用户位置进行精准的预测，则可以帮助平台快速判断在任务地点最有可能出现的用户，以此来避免因用户分布稀疏所造成的任务分配失败问题。

随着群智感知应用的深入，群智感知系统中关于用户位置预测的问题也得到了进一步重视[5]。目前在基于位置预测的群智感知任务中，应用最普遍的是马尔可夫模型。景瑶等人[6]提出一种针对移动性目标追踪的预测方法MPRE(Movement PREdiction)，根据用户的历史轨迹，利用马尔可夫模型对目标下一位置进行评估，并在此基础上分别提出了以人为中心和以任务为中心的2种智能算法对任务进行最佳分配，实现了对感知数据的实时获取。Yang等人[7]将马尔可夫模型作为核心技术，根据用户的历史行为轨迹，提出了一种基于兴趣点的移动性预测模型，用来获取用户可以完成任务的可能性。Wang等人[8]提出了一种基于预测的逆向拍卖激励机制，使用Semi-Markov模型预测下一刻的用户位置，根据预测位置选择具有最小移动距离和竞标价格的获胜者。

用户的位置序列是一个时间序列，用户每一时刻的位置都与他过去时刻和未来时刻的位置存在密切联系。在位置序列数据紧密连续的情况下，马尔可夫模型通常更适合用来处理时空数据，但是当数据中所包含的位置点稀疏时，马尔可夫模型在预测精度方面的表现则不佳。另外，马尔可夫过程只考虑当前的位置状态，并不受其历史位置状态的影响。近年来，许多学者和研究人员为解决位置预测等问题对人类的移动模式展开了研究，发现人类的行动位置可以被有效预测[9]。基于此结论，学者们针对位置的预测问题又提出了一些不同的解决方案。其中有学者充分利用卡尔曼滤波[10]和高斯模型[11,12]进行位置预测；Luan等人[13]提出一种名为XGBoost的基于树的位置预测模型来预测目标将要访问的下一位置；张震等人[14]提出了一种新型任务分配算法，并根据初始任务通过贝叶斯推理对用户活动的下一位置进行评估，消除了由于用户位置的可变性对数据实时性造成的负面影响；Xiao等人[15]利用支持向量机SVM(Support Vector Machine)回归来实现位置和轨迹预测，降低了计算复杂度，克服了维数灾难的问题。Jeong等人[16]采用深度神经网络DNN(Deep Neural Networks)进行位置预测，并用仿真实验证明了其有效性。但是，DNN无法对具有时序性的数据进行建模，使得预测结果达不到较高的精度。Choi等人[17]将循环神经网络RNN(Recurrent Neural Network)应用于预测位置中的下一地点。RNN可看作在时间维度进行传递的深度神经网络，对于序列数据建模非常有效。但是，在学习过程中因为考虑失效的历史信息会导致梯度消失或梯度爆炸问题，使模型预测精度下降。

用户的位置序列具有时序性，每个时刻的位置与其前后位置密切相关，因此针对群智感知中现有方法存在的问题，本文提出了一种基于门控循环单元GRU(Gated Recurrent Unit)的用户位置预测模型。首先分析对比了各种神经网络算法应用于用户位置预测的可行性，根据对用户位置时间序列的分析，搭建了基于GRU网络的用户位置预测模型。利用均方误差MSE(Mean Squared Error)等作为评价标准，对网络模型参数中的迭代次数和批次大小进行调优；并根据交叉熵代价函数选取了Adam优化器。最后对所提模型进行了仿真对比分析。

2 基于位置预测的群智感知系统模型

对于群智感知系统，位置预测可以极大提高任务的分配效率。在基于位置的群智感知应用中，时常会出现某些时刻用户数目无法充分覆盖感知区域的现象(当下时刻位于任务地点的用户数目稀少或几乎没有，达不到任务完成所需数量)，对任务完成产生负面影响。因此，可通过位置预测为群智感知系统提供用户现在及将来时刻位置，并配合相关激励机制，增加参与者数量，保证感知任务顺利完成。图1为本文提出的系统模型，感知服务平台根据预测的用户未来时刻位置进行任务分配，其中请求服务的一方称为任务请求者，被感知服务平台锁定为执行任务的备选者称为用户。

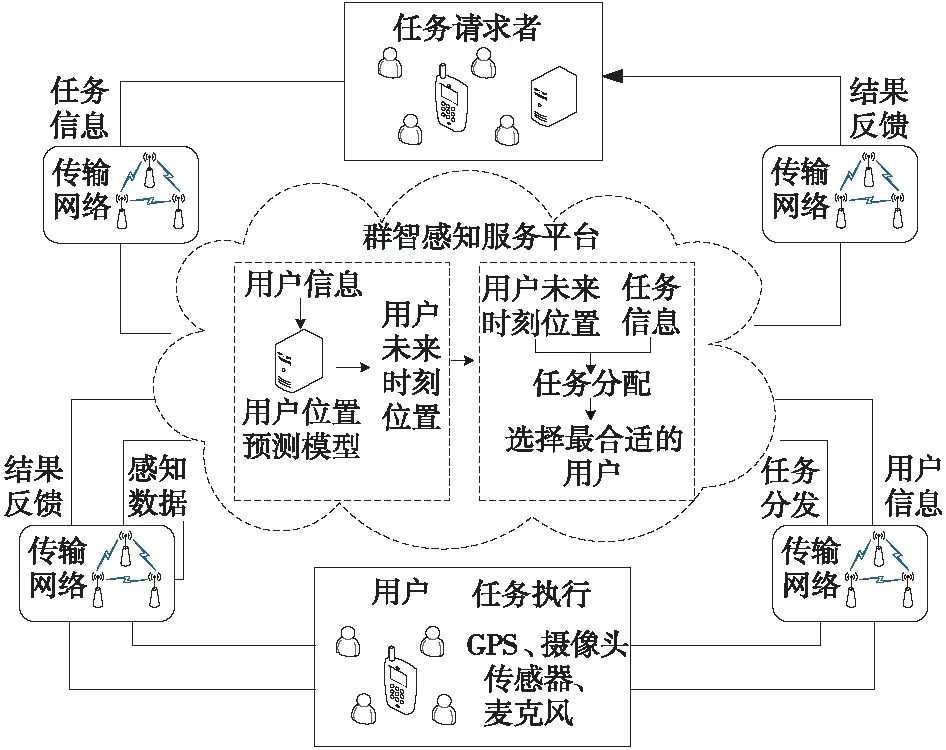
Figure 1 Model of the crowd sensing system图1 群智感知系统模型

如图1系统模型所示，平台对任务备选者的未来时刻位置进行预测，然后将其与发布的任务信息进行匹配，最后通知被选定的用户并给出任务执行的下一步指示,确保有效执行任务。用户向平台提供包括GPS位置坐标和时间戳等自身信息，用一个6元组表示：ID是用户的标识符，x、y、v和e分别代表用户在t时刻的经度、纬度、速度和所在路段。突发紧急任务的情况下，感知平台利用用户的历史位置数据立即对用户未来位置进行预判，并根据接收到的任务的时间和位置等信息分配任务。分配完成后，平台会通知所选用户。用户根据任务指令在一定时间内到达指定的任务位置，并利用现有设备采集信息，经过简单的处理和计算，将数据上传至服务平台，完成此次任务。

3 基于GRU网络的用户位置预测算法

通过对人类运动轨迹的研究发现，人类的出行活动存在着较高的重复性，会在固定的时间段内，在相对固定的地点进行一些日常活动[9]。因此，本文提出了一种基于GRU网络的用户位置预测算法，利用对用户的历史出行位置时间序列模型的研究，预测用户将来某个时刻可能到达的地点；同时，利用Adam算法对GRU网络进行优化，使得预测结果更加准确。

3.1 GRU网络结构

对于用户历史出行位置的时间序列的分析要求算法具备记忆功能，能够记录用户历史位置数据特征。作为神经网络的RNN、长短期记忆LSTM(Long Short-Term Memory)网络和GRU都具有记忆功能，适用于处理时间序列。相较于普通的神经网络RNN增加了一个循环机制，将上一个隐含层的输出结果作为条件加入当前隐含层的结果判断。如图2所示，对于一个标准的RNN模型，其输入序列为x={x1,x2,x3,…,xn}，通过模型计算可得到隐含层的序列h={h1,h2,h3,…,hn}和输出序列y={y1,y2,y3,…,yn},其中x、h、y均为向量，分别代表输入层、隐含层及输出层的值，U、V、W分别是输入层到隐含层、隐含层到输出层和隐含层内的权重矩阵。

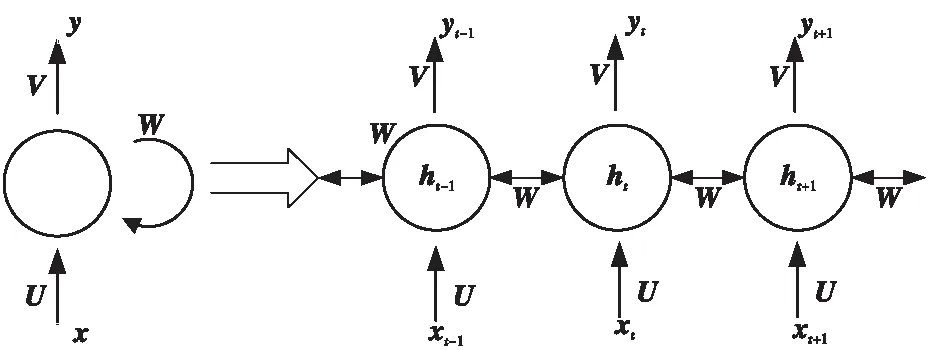
Figure 2 RNN time line expansion图2 RNN时间线展开图

具体公式如式(1)和式(2)所示：

ht=tanh(Wx*xt+Wh*ht-1+b)

(1)

yt=Softmax(Wsht)

(2)

其中，tanh、Softmax是激活函数，Wx、Wh、Ws分别为输入层、隐含层和输出层的权重，b为偏置。ht、ht-1分别是t和t-1时刻隐含层的值，yt是t时刻的输出值，都为向量。

用户未来时刻位置的预测依赖于对用户历史位置时间序列的分析，时间序列越长，记录的用户历史运动轨迹数据越多，预测精度相应也会越高。但是，RNN的记忆能力相对有限，信息积累到一定时间长度时，初始的信息便会消失，无法解决长期依赖的问题。相较于RNN，LSTM引入了门(Gate)的概念，通过输入门、输出门、遗忘门来选择或遗忘数据特征，实现了序列数据的长距离依赖，解决了RNN的梯度消失问题。GRU在LSTM网络的基础上进行了改进，其网络结构如图3所示，它只包含更新门和重置门，去掉了单独的存储单元，使用隐藏状态传递数据特征。

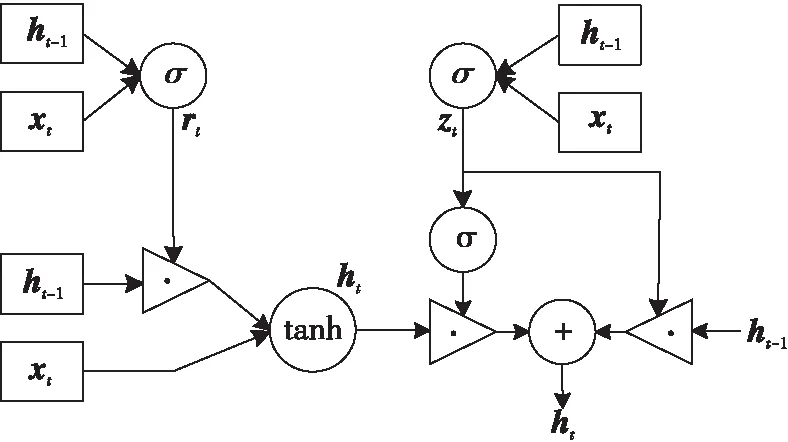
Figure 3 GRU unit structure图3 GRU单元结构

GRU单元的更新可分为如下几个步骤(其中xt和ht分别代表t时刻的输入和输出数据)：

zt=σ(Wxzxt+Whzht-1)

(3)

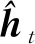
rt=σ(Wxrxt+Whrht-1)

(4)

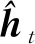
(5)

其中，⊙表示Hadamard乘积。

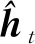
(6)

3.2 基于GRU网络的用户位置预测模型

用户在现实生活中的运动都会受到路网条件的限制，因此在构建用户运动模型时考虑路网因素具有重要意义。将路网结构定义为一个有向图Q=〈S,E〉，S与E分别表示节点与边的集合。其中每个节点si(si∈S)对应路网中的交叉路口，每条边e=(si,sj)(si,sj∈S,e∈E)表示2个路口si与sj之间的路段，且表示方向为由节点si朝向节点sj。每个节点si(si∈S)都分别对应着一个经纬度坐标点p={x,y}，如图4所示。

Figure 4 Road network structure图4 路网结构

用户位置预测问题实际上是一种利用GRU网络的回归性问题。此模型中的网络输入为用户的历史位置特征和当前位置特征，网络输出为用户在未来某一时刻的位置特征数据。通过预测值与真实值的误差对比来训练网络，以此建立用户位置的历史特征数据与未来特征数据之间的函数关系，实现对用户未来位置特征的评估。针对单个用户在GRU模型的数据输入轨迹特征可表示为：

(7)

根据用户历史轨迹坐标p映射到图Q中边上的位置li，那么用户的轨迹实际上是一系列位置li按时间纬度进行排列的时间序列，位置点集合可表示为Loca=〈l1,l2,…,li〉。li表示用户位置中的第i个位置点，其可表示为li=〈xi,yi,vi,ti,ei〉，其中，xi，yi，vi，ti，ei分别代表用户在第i个位置点时的经度、纬度、速度、时间以及对应图Q中的所在路段。对GRU模型的输入而言，位置的时间序列表示为Xt=[lix,liy,lit,liv,lie]，用户位置表示为X=[X1,X2,X3,…,Xt]。为了实现用户位置的预测，本文将连续前k个时刻的用户位置数据X(t-k+1),…,X(t-1)和X(t)作为GRU模型的输入，t+1时刻的用户位置X(t+1)作为模型输出，用户位置预测模型的表达式如式(8)所示：

X(t+1)=f({X(t-k+1),…,X(t-1),X(t)})

(8)

为加快梯度下降中求取最优解的速率并减少预测误差，将模型的输入数据进行归一操作，使数据的取值统一于[0,1]。采用离差标准化(Min-Max Normalization)进行归一化，转换公式如式 (9)所示：

(9)

其中，Xmax为样本数据中的最大值，Xmin为样本数据中的最小值，X代表初始训练数据，X*代表归一后的数据。归一化处理可以有效地避免数据数量级和取值范围不同的影响。利用GRU网络对用户位置进行预测后的结果所处量级依旧在[0,1]，无法直接判断与真实值之间的误差，因此需要对结果按式(10)进行反归一化处理，即式(9)的逆运算，才能得到实际的预测结果y。

y=X*(Xmax-Xmin)+Xmin

(10)

算法1基于GRU网络的用户位置预测算法

输入：用户位置序列Xposition,待预测用户位置序列Xtext。

输出：用户下一时刻的位置Xresult。

BEGIN

构建训练数据集，输入连续k个时刻X(t-k+1),…,X(t-1),X(t)的位置特征数据;

通过式(9)对输入数据进行归一化处理；

训练集合Xposition中的每条数据，并保存训练结果{data}；

将训练数据{data}输入GRU网络;

计算误差函数，并利用Adam算法更新GRU参数，得到最佳GRU网络模型;

将待预测用户位置序列Xtext输入训练完成的GRU网络模型;

根据式(8)得到用户下一时刻的位置Xresult;

END

由算法1可以看出，用户位置预测算法包括训练和预测2部分。在训练阶段，将子轨迹数据进行归一化处理之后，对于每一条历史轨迹序列,取前k个时刻的轨迹点作为子序列加入到训练数据集中，将第t+1时刻轨迹点作为预测目的点，加入到目标数据集中，利用训练集对GRU网络模型进行训练，并采用Adam算法对模型参数进行优化。最终利用GRU网络模型得到所需要的下一时刻位置点，并对所得结果进行反归一化处理，得到预测结果。

3.3 Adam优化算法

为了加快权值矩阵的训练，本文采用Adam算法作为预测用户位置的GRU网络的梯度训练算法。该算法把AdaGrad (Adaptive Gradient Algorithm)算法[18]和RMSProp (Root Mean Square Prop)算法[19]的优点结合起来，提高了参数更新和梯度更新计算的效率，减少了内存使用，而且能够解决梯度稀疏或梯度噪声大的问题。如算法2所示：

算法2Adam优化算法

输入：全局学习率η(默认值为0.9);矩估计的指数衰减速率：β1，β2∈[0,1)(一般分别取0.9和0.999);用于数值稳定的小常数δ(默认值为10-8);初始参数W0。

初始化一阶和二阶矩变量m0=0，v0=0;

初始化时间步t=0;

whileWt没有收敛do

计算梯度：gt←▽J(Wt-1)(J为代价函数，得到随机目标在时间步长t处的梯度);

更新时间步t;

更新有偏一阶矩估计：mt←β1mt-1+(1-β1)gt;

更新参数：Wt+1←Wt+Δw;

endwhile

4 仿真实验

为了验证GRU网络在群智感知中对于用户位置预测的有效性，本文实验基于深度学习框TensorFlow 2.0版本的上层框架Keras，构建了基于GRU网络的用户位置预测模型。为了优化模型，提高模型的预测精度，通过模型自身对比实验寻找最优参数。在相同实验环境下，通过与RNN和LSTM模型的对比，来验证基于GRU网络的用户位置预测模型的有效性。

4.1 实验数据集

车辆的出行数据不仅记录了车辆的行车位置，还蕴藏着居民的出行规律[9]。因此，本文实验采用来自于实际路网数据收集的城市区域车辆行驶的GPS位置信息[20]。实验采用市内车辆在2014年7月31日至8月12日的部分有效出行数据，并将路段信息进行标号，使路段e1,e2,…,em分别对应为序号1,2,…,m。这些数据很好地反映了当前城市区域内车辆行驶的位置、时间等信息，可以作为本文的实验数据使用。表1所示为车辆位置的部分GPS数据。

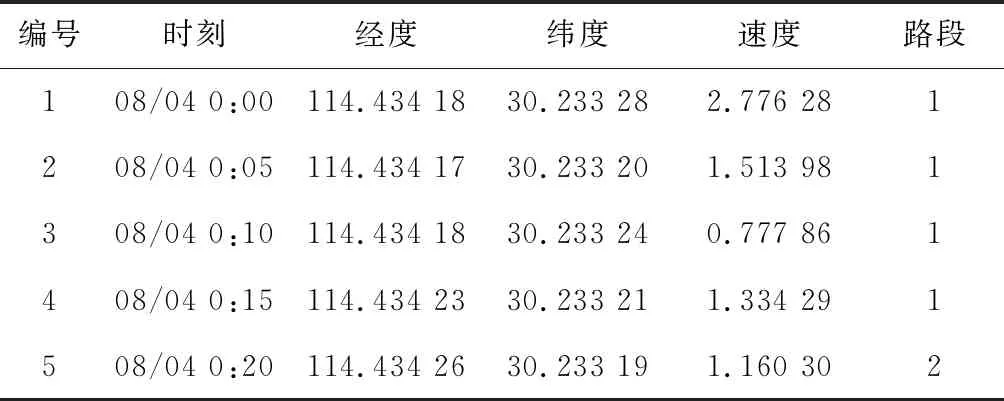
Table 1 Segment of vehicle trajectory data set

在实验部分为了使GRU预测模型更具有说服力，将数据集划分为65%训练集和35%测试集，同时为了验证本文模型的精度设置了5%验证集。

4.2 实验内容

为了更好地评价、分析和预测结果，本文采用MSE、平均绝对误差MAE(Mean Absolute Error)和平均绝对百分误差MAPE(Mean Absolute Percentage Error)作为评价标准。MSE的数学表达如式(11)所示，这里用作网络预测模型的loss值，loss值的大小代表着位置预测模型的预测精度。MAE和MAPE的数学表达分别如式(12)和式(13)所示，2种误差指标为0%时表示模型完美，大于100%则表示模型劣质。

(11)

(12)

(13)

4.2.1 模型参数分析

适合的参数可以优化网络模型的性能，因此实验针对迭代次数epoch、批次大小batchsize2个参数进行对比分析。将均方误差作为评价指标，对上述样本进行不同参数值的训练学习，部分结果如表2所示。

Table 2 MSE for different parameters

如表2所示，实验中总计数据量为6 428条，通过比较最终确定epoch=500，batch_size=128时均方误差最小，结果为2.49E-05。说明在当前参数配置下的GRU网络模型表现出最好的预测能力与精度。

为了实现模型的最优化，使得用户位置预测结果的误差尽可能小，要选择合适的优化器来寻找网络合适的参数。Adam算法与RMSProp算法都可以对GRU网络的参数更新和梯度更新进行优化，在相同的实验环境下进行对比，图5为分别采用2种优化算法的训练效果。

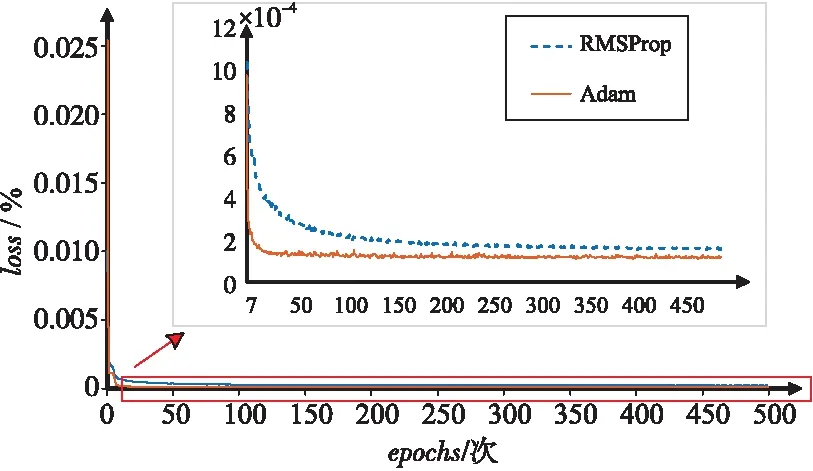
Figure 5 Optimizer training results图5 优化器训练结果

如图5所示，2条线分别代表基于GRU的用户预测模型中训练损失loss的变化。RMSProp和Adam优化器在第1次训练时达到的loss值分别为0.018和0.012，此时模型所表现的精度不够。继续训练可以看到使用Adam算法的loss值在第13次训练时迅速下降到了1.95E-04，并且很快收敛，在相同的时间段内RMSProp的表现稍逊色一些。从整体效果来看，在2种优化算法作用下，训练损失loss值都处于下降收敛的趋势，但是Adam算法的优化效果明显比RMSProp好，更适用于本文实验规模数据和参数训练场景，所以最终选取Adam优化器完成基于GRU的用户位置预测模型的训练。

4.2.2 模型质量分析

通过上述对用户位置预测模型的参数寻优调整后，其训练后的MAPE结果如图6所示，实线代表基于GRU用户预测模型中MAPE值的变化。MAPE是作为当前训练得到的模型好坏的一个“可视化”指标。开始训练时MAPE值达到了255%，说明此时所训练的模型不够成熟。但是，伴随迭代次数的不断增加，MAPE值也随之减小，并最终降至6.11%,趋于稳定，经验证与之对应的测试集误差也在减小，说明经过参数优化后的基于GRU的用户预测模型效果良好。

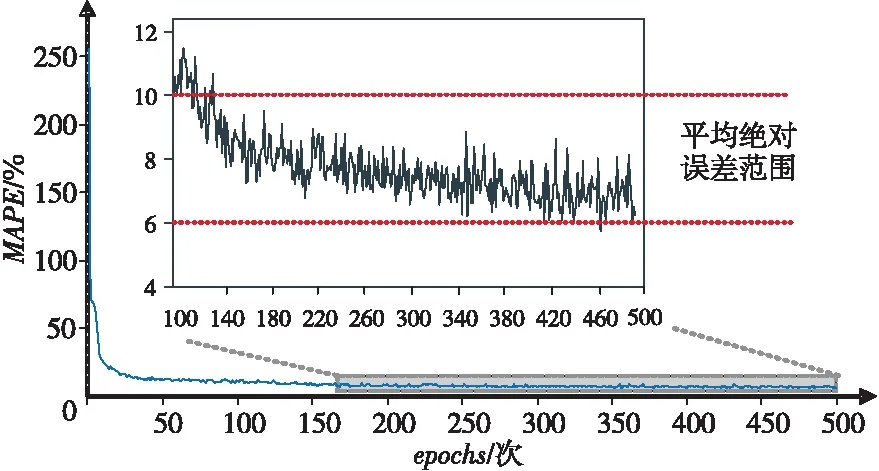
Figure 6 MAPE value of the model图6 模型的MAPE值

4.2.3 用户位置预测效果

为了更清晰地表达预测位置的精度，在此分析了预测位置与实际位置的误差。根据确定的GRU最佳迭代次数、批次大小以及优化器选型，将3个时刻的用户位置数据作为初始输入，预测接下来的4个点的用户位置，得到的预测位置与实际位置的误差结果如图7所示。

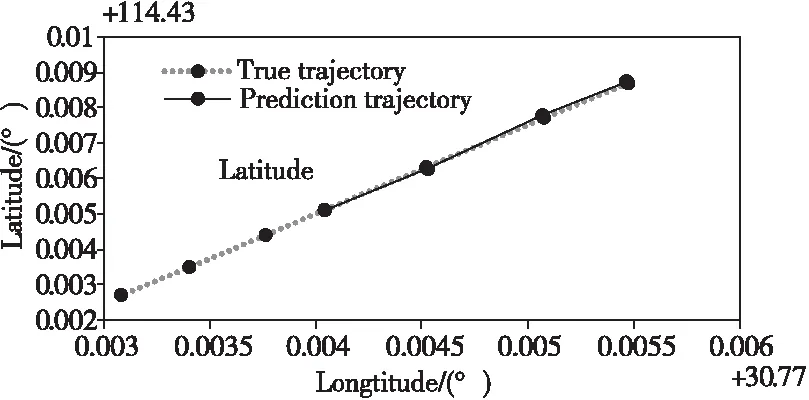
Figure 7 User location prediction图7 用户位置预测

从图7中可看出，预测位置(黑色折线4个点)与实际位置(灰色折线)近乎重叠。同时输出的路段信息根据本文所定义的路网结构可判断用户的移动方向，按照式(14)，利用前一时刻t的位置以及预测得到的速度和方向推测下一时刻t+1位置，所得结果与图7的一致，说明模型的预测精度较高，可以满足群智感知系统要求。

pt+1=pt±vt

(14)

4.3 实验结果

分别使用GRU模型、LSTM模型和RNN模型对样本进行训练，在输入的测试数据及历史时刻的用户位置特征(数据格式如式(7)所示)完全相同的情况下，以递归方式进行连续预测，得到预测模型对于训练集和测试集的拟合精度，如表3和表4所示。

Table 3 Training results of different models

Table 4 Test results of different models

由表3可知，GRU与LSTM较RNN而言，训练时间长，约为RNN的2倍，但预测误差小，其内部原因在于这2种模型作为深度递归网络，具有联想记忆功能和遗忘机制，网络进化时间较长。同时，GRU由于参数少，结构较LSTM更加简化，所以拥有更快的训练速度，训练时间比LSTM节省8.3%，并且GRU的MSE和MAPE分别比LSTM的低18.0%和1.1%。同时，在表4所示的测试集结果中，GRU的MSE和MAE分别比LSTM的低33.3%和58.2%。

5 结束语

本文针对在群智感知环境中用户位置预测的精度问题，并根据位置数据可变性大、非线性强的特点，将门控循环单元引入到用户位置预测中。模型引入了Adam优化算法迭代更新GRU网络权重，有效地提高了GRU网络预测的精度及优化效率。同时，使用均方误差作为选择参数的评价指标，平均绝对误差和平均绝对百分误差分别作为测试结果和判断调试后模型优劣的评价标准。将RNN、LSTM和所提的GRU网络模型进行对比实验，对3个模型的训练时间及预测精度进行了定量研究。仿真实验表明，本文提出的基于GRU网络的用户位置预测算法的预测精度高于经典的RNN和LSTM算法，可以为群智感知系统提供用户未来时刻的准确位置，进而有效地进行任务分配工作，提高群智感知系统效率。本文研究的最终目的是通过对用户位置的准确预测来实现任务及时有效的分配，所以下一步研究的重点是在已知用户未来位置的基础上提高感知任务的完成效率。