一种改进的差分隐私参数设置及数据优化算法 *
2021-10-26胡雨谷葛丽娜
胡雨谷,葛丽娜,2
(1.广西民族大学人工智能学院,广西 南宁 530006;2.广西民族大学网络通信工程重点实验室,广西 南宁 530006)
1 引言
大数据、物联网规模与日俱增,全球参与设备的数量数以亿计。每个连接到互联网的设备或多或少不断地产生着各种各样的数据,其中可能含有用户的隐私信息。当包含隐私数据的设备接入互联网并提供数据给其他设备访问时,用户的隐私便存在被暴露的风险。如何控制和协调产生数据的设备与访问数据的设备之间的访问是一个难点。因而构建安全可用的数据访问处理方法是实现数据访问控制的重要研究方向之一。Dwork[1]提出的差分隐私DP(Differential Privacy)有着严格数学证明,其隐私预算参数ε改进了传统隐私保护模型需要背景知识假设和无法定量分析隐私保护水平的不足,从而能够对数据的隐私安全提供良好的保障。
文献[2]利用概率知识,给出了一种基于背景知识的攻击模型,并计算出差分隐私预算ε的上限。文献[3]则基于Laplace机制,对差分隐私的结果进行查询分析,并依据结果推导数据集中是否含有攻击对象,继而得出攻击者的成功概率和优化的差分隐私预算ε的上界。文献[4]提出启发式策略LPBDP(Limit Privacy Breaches in Differential Privacy),使得隐私参数ε的设置不再依赖于经验或实验,而是可以根据查询值的先验概率与后验概率进行启发式设置。文献[5]研究了选择差分隐私预算ε和δ时必须考虑的关键因素,提出了一个简单的经济模型,使差分隐私用户能够根据实际可估计的量,有原则地选择差分隐私预算参数。文献[6]则在文献[4,5]的基础上,依据置信分析过程,设计了差分隐私预算配置算法。
现有的研究大都集中在对公式理论的改进,忽视了实际的应用场景,往往不能很好地从数据的使用者和数据的提供者角度着手,去满足现实隐私的需求。
本文充分考虑应用场景,根据数据访问者和贡献者的信誉度信息,并与数据隐私度以及访问权限值关联,设计了基于信誉的差分隐私参数设置算法RBPPA(Reputation for differential privacy Based Privacy Parameter setting Algorithm),实现了细粒度的隐私参数设置。针对满足隐私保护的加噪数据可用性降低的问题,设计了基于平方根无味卡尔曼滤波的差分隐私数据优化算法DPSRUKF(Differential Privacy data optimization algorithm based on Square-Root Unscented Kalman Filter),对加噪数据进行优化[6,7],以提高差分隐私数据的可用性。
2 差分隐私的隐私参数设置算法
本文所提出的算法基于如下应用场景:用户甲的设备产生了一些数据,并有选择地向其他设备开放数据的访问权限,下文称为数据贡献者DC(Data Contributor);用户乙、丙和丁等众多用户需要访问用户甲的设备产生的数据,下文称为数据访问者DV(Data Visitor)。图1所示为本文所提算法的应用场景示意图。

Figure 1 Application scenarios图1 应用场景示意图
面对这样的场景,从数据贡献者DC的角度出发,首先会考虑自身数据的安全性,通过差分隐私技术提供数据隐私的保护;从数据访问者DV的角度出发,首先会考虑所请求的数据的完整性、可用性等。为此,综合两者的利益,基于两者的信誉度设计细粒度的隐私参数设置算法,实现了在使用敏感数据时保证其隐私得到保护。
2.1 差分隐私
差分隐私在强大的数学模型基础上严格定义了攻击模型,对隐私泄露给出了严谨、定量化的表示和证明,使得人们可以对不同参数下的数据集的隐私保护水平予以评估和比较。差分隐私有2个最基本的实现机制,针对数值型数据采用Laplace机制,而针对非数值型的数据可采用指数机制[8]。
定义1(差分隐私) 设给定一个随机隐私函数M是满足(ε,δ)-差分隐私的,如果2个数据集D1和D2之间只相差1个元素,即‖D1-D2‖1≤1,对所有S⊆Range(M),有:
Pr[M(D1)∈S]≤eε·Pr[M(D2)∈S]+δ
其中,Pr[·]为概率表示,ε为隐私保护的预算值。其中,若δ=0,称算法M满足(ε,0)-差分隐私。
定义2(Laplace机制) 对于任一函数f:N|χ|→Rk,Laplace机制定义如下:
ML(x,f(·),ε)=f(x)+(Y1,…,Yi,…,Yk)

根据定义1可知,对仅有1个元素不同的相邻数据集,随机算法M的输出结果由隐私预算ε和参数δ决定。ε越小,其隐私保护程度越高,当ε=0,δ=0时,有:
Pr[M(D1)∈S]≤e0·Pr[M(D2)∈S]+δ⟹
Pr[M(D1)∈S]≤Pr[M(D2)∈S]+δ⟹
Pr[M(D1)∈S]=Pr[M(D2)∈S]
因此,ε=0,δ=0时,M对D1和D2的查询结果完全相同,数据的可用性完全丧失。
2.2 隐私参数设置算法
本文的隐私参数设置算法是在李森有等人[9]的研究基础上改进与完善的,通过对数据共享者与数据访问者的信誉度值、数据贡献者对数据隐私安全级别的设置值,动态确定数据访问者查询数据获得的安全可信度等级,以获得相应的隐私保护预算,实现细粒度的访问控制。
为了实现数据贡献者的隐私数据安全,同时使数据访问者最大化地利用共享数据,基于数据贡献者与数据访问者的信誉度,本文提出了差分隐私参数设置算法RBPPA。RBPPA的组成结构如图2所示,表示了数据访问控制的信息流向。
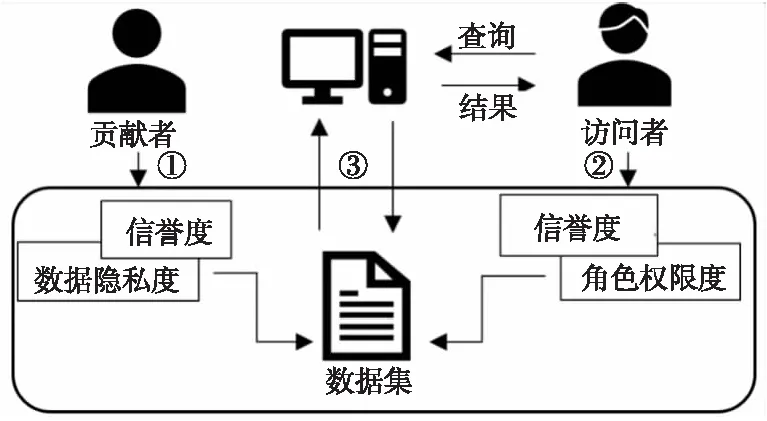
Figure 2 Composition of RBPPA图2 RBPPA的组成结构
(1)读取数据贡献者的信誉度,设定其贡献的数据隐私保护度的值;
(2)读取数据访问者的信誉度,找到其角色属性相应权限度的值;
(3)利用(1)与(2)得到的数值,计算数据的隐私保护预算值ε,进一步计算其加噪后的数据值。
RBPPA算法中,对数据查询的可信度由数据访问者与数据贡献者双方的信誉度共同决定,他们的信誉度值越大,就能够查询到越接近真实值的数据;同时,数据贡献者有对所贡献数据设置隐私保护程度的权力,其值越低则可查询到的数据越接近真实值。
首先,计算查询安全可信度QC(Querying security Credibility)和数据贡献者可信度 :
查询安全可信度QC由数据访问者的可信度DVC(Data Visitor Credibility)和数据贡献者的可信度DDC(Data Dedicator Credibility)通过加权计算而得,即QC的计算方式如式(1)所示:
QC=α·DVC+β·DDC
(1)
其中,α、β为权重,且α+β=1,α和β的值根据访问者的信誉度Vrep和贡献者的信誉度Drep进行设置,即如式(2)所示:
α∶β=Vrep∶Drep
(2)
通过调节α和β,可以动态地实现对数据精确、实时的隐私保护[10]。
根据α+β=1和式(2),可以得到:
(3)
设访问者可信度DVC是Vrep和访问者对应的角色属性权限度Vper的函数,表示为函数f(Vrep,Vper)。Vrep和Vper是服从0~1之间正态分布的随机变量,选用二维Gauss函数作为相应的函数,DVC的计算方式如式(4)所示:
DVC=f(Vrep,Vper)=
(4)
设数据贡献者可信度DDC是Drep和对应客体资源所设置的数据隐私度Dpri的函数,表示为函数g(Drep,Dpri)。对式(4)进行调整,得到DDC的计算如式(5)所示:
DDC=g(Drep,Dpri)=
(5)
结合式(1)~式(5),可以得出查询安全可信度QC的计算方式如式(6)所示:
(6)
然后,设置QC与隐私预算参数ε的一一映射关系。
由式(6)计算出QC的最大值QCmax和最小值QCmin,均等分可信等级区间 [QCmin,QCmax]成n(n≥3)个等级;同样,也均分隐私预算参数ε为n份,与可信等级相对应。
设定各个可信等级与隐私保护参数εi的对应关系,即第i个可信等级的区间表示为:
其对应的隐私保护参数为εi。由此建立了从安全可信度值区间到隐私参数值区间的映射关系,该映射为一对一的。于是,可通过查询该映射关系,实现隐私参数的细粒化设置。值得注意的是,若QC的值区间固定,同时全体数据访问者的ε参数的取值均来自同一值区间,则优劣者之间的差异程度无法实现,难以观测得到优者越优、劣者越劣的系统增益。因此,引入ε值估计法,通过置信区间和置信水平的设置来表达真实值在间隔估计中准确性的提升。


(7)
定义4(误差尺度) 误差尺度w表示为噪声数据所被允许的误差比例,且w∈(0,1)。
定义5(输出概率) 数据贡献者在共享数据时,设置数据的误差尺度为w,且被访问的概率为p,且p∈(0,1),即数据以w误差尺度的输出概率为p。
定义6(隐私保护级别) 假设以误差尺度w为置信区间的大小,以输出概率p为置信水平,则隐私保护级别P可用式(8)进行定义:

(8)
继而将式(7)代入式(8),可以得到式(9):

P[(1-w)·c F(wc)-F(-wc)= (9) 其中,F(·)为累计分布函数,b=Δf/ε。通过式(9)可看出,随着真实值c的增长,ε值就越小,噪声越大,可用性越小,隐私保护越强。 当增强数据的隐私保护时,其可用性就会被降低,所以需要在这两者之间进行折衷。为此,本文优先考虑可用性,采用ε区间取值方法,由式(9)可知,为了取得越小的ε值,则要求误差尺度w尽可能地大。这与可用性优先所要求的误差尺度w尽量小是不吻合的。为此,w可采用1与数据访问者对应角色的权限最小值之差,即wmax=1-Vpermin,Vpermin表示数据访问者所在机构角色权限的最小值,这样数据访问者的权限更大、级别更高时,则得到的数据更精确。 与此同时,为了最小化ε的值,需等价最小化输出概率p。此时的p值可以表示为数据贡献者的信誉度,于是有pmin=Drepmin。由于0 Table 1 Query trust level and privacy budget parameter comparison 由此可见,与基准算法相比,改进的隐私参数设置算法,在一定程度上缩小了隐私预算参数的取值区间,这就使得数据访问者的信誉度越高时,获得的数据添加的噪声就越小,数据的可用性就越高;算法中将数据的信任等级、查询安全可信度与隐私预算一一对应,使得数据贡献者与数据访问者的交易更方便。本文提出的RBPPA如算法1所示。 算法1RBPPA 输入:Vrep,Vper,f(V)=(Vrep,Vper),Drep,Dpri,g(D)=(Drep,Dpri),n,w,p。 输出:εi。 步骤1初始化Vrep,Vper,Drep,Dpri; 步骤2 foreach access request: 步骤4f(Vrep,Vper)=exp 步骤 5DVC=f(Vrep,Vper); 步骤6foreach objects: 步骤8DDC=g(Drep,Dpri); 步骤9endfor 步骤10QC=α·DVC+β·DDC; 步骤11endfor 步骤14endfor 步骤15QCmax= 1;QCmin= 0; 步骤16forQCin [QCmin,QCmax]: 步骤17把[QCmin,QCmax]平分为n等份; 步骤18对照表1,查出QCi对应的εi; 步骤19endfor 步骤20returnεi. 首先,对提出的与QC区间进行一一映射的ε最小值区间的确定方法进行实验验证与分析,设式(6)QC映射的结果表示为εi-old,设将系统中各参数的最大、最小值代入式(6)后确定与QC映射的结果表示为εi-new,将其与映射关系中QCi进行对比。从图3右向左看,可以看出,当访问者权限变小时,εi-old与εi-new之间的差值在变大。实验表明,给定的εmin的值在随着访问权限的减少而减少,并且εmin越来越接近0。而且,经过重新划分后映射出的ε值相对于原值稍有提升,提高了数据的可用性。 Figure 3 Relation of data visitor permission values and privacy parameters图3 访问者权限值与隐私参数的关系 图4给出了εi-new与输出概率p和误差尺度w百分比的关系。图4表明,当访问者有较高的权限时,其有较大的输出概率,它的误差尺度就会较小,其εi-new较大,则有较高的数据可用性。该结论与实际需求一致。由此验证了p和w的引入是合理的。 Figure 4 Relation of privacy budget, output probability and error scale图4 隐私预算与输出概率和误差尺度的关系 在第2节差分隐私的隐私参数设置算法设计中,从保护数据贡献者的角度出发,通过将细化映射预算分配所获得的隐私预算参数与差分隐私技术结合,实现对数据的扰动处理。但是,对于数据访问者,其关心的重点则是数据的可用性,包括数据的精确程度、来源的真实程度等。为了更好地保障访问者的数据可用性需求,本文在文献[12]所提出的无味卡尔曼滤波DPUKF(Differential Privacy algorithm based on Unscented Kalman Filter)提升数据精度的办法之上进行改进,引入平方根形式的矩阵分解方法[13],提出基于平方根无味卡尔曼滤波的差分隐私数据优化算法DPSRUKF,缩小计算的误差[14,15],从而实现数据精度的再提高。 DPSRUKF算法流程框架如图5所示。 Figure 5 Framework of DPSRUKF algorithm图5 DPSRUKF算法流程框架 依照图5,DPSRUKF算法流程表述如下: (1)读取关于数据访问者的访问权限等有关的数据隐私保护参数; (2)读取被访问数据对应的隐私预算,根据隐私预算值,对数据添加Laplace噪声; (3)将含有噪声的数据传给平方根无味卡尔曼滤波处理器进行处理,实现优化处理; (4)如果(3)的结果是正优化,则完成数据隐私保护和优化,并递交给上一层客体访问点;否则,如果是负优化,则转向(2),对数据重新进行优化处理。 算法2DPSRUKF算法 输入:原始数据向量集{xi(0)}(i=1,2,…,n),ε。 输出:加噪并优化后的数据向量集{ri(k)}。 步骤2 whileture 步骤3 foreach data in {xi(k)}: 步骤4x′i(k)=xi(k)+Lap(λ); 步骤6Xi,k|k-1=Fi(k-1,ξi,k-1); 步骤18Si(k)=cholupdate{Si(k,k-1), Gi(k)Si,yy-1}; 步骤20k=k+1; 步骤21if{ri(k)}比{xi(k)}精度更高: 步骤22return{ri(k)}; 步骤23 endif 步骤24 endfor 步骤25 endwhile 定理1DPSRUKF算法是满足ε-差分隐私的。 证明函数f:D→Rn,若 f(D)=(x1,x2,…,xn)T f(D′)=(x′1,x′2,…,x′n)T= (x1+Δx1,x2+Δx2,…,xn+Δxn)T 则有: 设xi=0,f(D)=(0,0,…,0)T,f(D′)=(Δx1,Δx2,…,Δxn)T,O=(y1,y2,…,yn)T,有 由上面的推导可知,对每个xi查询满足了差分隐私保护,隐私预算为εk=ε/M,由于差分隐私满足组合性质,所以 DPSRUKF算法是满足ε-差分隐私的。 □ 实验测试一组普通非线性函数,隐私预算参数取0.5。设置对比实验,分别对比真实数据、加噪值(对真实数据按差分隐私要求添加拉普拉斯噪声之后的称为“加噪值”)、无味卡尔曼滤波DPUKF算法输出数据和DPSRUKF算法输出数据,结果如图6所示。 Figure 6 Comparison of estimated deviations图6 估计偏差对比 表2表明,DPSRUKF算法优化了DPUKF算法的数值,提高了加噪数据的可用性。 进一步,隐私预算ε取0.1,0.01,在不同ε下比较产生的误差值平均值,结果如图7所示。通过图7可以看出,隐私预算的值与误差值负相关,隐私预算的值越小,误差越大,即数据的可用性越小。因此,DPSRUKF算法能够有效提升隐私数据的可用性。 Table 2 Root mean square error RMSE Figure 7 Comparison of error values under different ε图7 不同ε下的误差值对比 本文提出了一种基于信誉度、数据隐私权限和数据访问者权限相互关联的差分隐私的隐私参数设置算法和一个加噪数据优化的算法。隐私参数设置是建立在隐私参数查询安全可信度一一映射的基础上,设计了隐私参数的细粒度设置方法,实现用户对隐私更自主的保护,提高了差分隐私技术的灵活性和有效性;针对加噪数据可用性降低的问题,采用了平方根无味卡尔曼滤波算法进行处理,使数据的可用性得到提高。下一步的工作将完善去中心化下共享机制的隐私保护技术,助力构建更加公平、公开、高效安全的网络共享共治平台。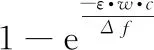



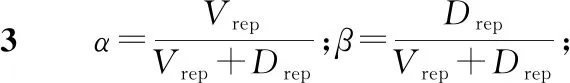
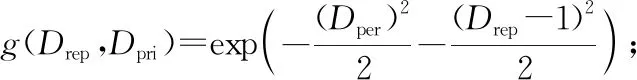


2.3 实验分析


3 加噪数据优化算法
3.1 DPSRUKF算法流程

3.2 算法表述


















3.3 分析与实验




4 结束语
