利用粒子群算法实现陀螺仪耦合系统动态响应优化*

王继寅，薛 旭

(1.中国科学院地质与地球物理研究所/中国科学院油气资源研究重点实验室,北京 100029；2.中国科学院大学,北京 100049；3.中国科学院地球科学研究院,北京 100029)

半球谐振陀螺是固体波动陀螺的一种,不同于传统的含有转子利用旋转惯性的陀螺传感器,固体波动陀螺利用振动元件对转动输入角速度敏感从而进行测量,在激发状态下,因为哥里奥利力的存在,激励模态会让敏感模态产生与陀螺自身属性和外界输入相关的振动,用于空间和钻地等姿态调整[1]。

在陀螺仪控制的策略中,一般采用平均法和深度负反馈对陀螺仪的能量、相位等实现控制,让陀螺仪工作在目标状态。深度负反馈的工作可以利用PID 控制方法实现[2]。在陀螺仪的空间应用中或者地下钻井应用中,要求深度负反馈的控制稳定误差和输出漂移更小,但陀螺仪的控制稳定时间较长；一些大机动平台要求有更快的响应速度和更宽的量程范围。PID 参数的确定方法一般是利用Simulink 对控制系统模拟,模拟参数控制效果再在真实系统上加以实现。国内对于控制参数的选取已经有一些方法,上海交通大学团队利用PID 控制实现了陀螺仪控制效果,但是对于控制结果并没有加以优化；东南大学团队通过系统的开环带宽设计系统控制参数；苏州大学团队基于MEMS 陀螺,通过利用去耦合的解析方法得了控制参数[2-4]。

在单输入输出(single-input-single-output,SISO)系统PID 控制参数整定的方法中,利用PSO 方法(粒子群算法)实现了动态响应的优化[5-8]。但是对于复杂的陀螺仪耦合控制系统没有设计方案和应用方案,通过传统去耦合带宽设计法、PID 参数控制效果拟合方法以及PSO 优化方法加以比较,探究PSO方法在陀螺仪控制动态响应上的优化作用。

1 陀螺仪工作原理与测量方案

固体波动陀螺的物理模型建立依托的是由Love 提出的薄壳模型,薄壳模型符合对于处于微小振幅状态的固体波动陀螺的合理假设,在考虑到刚度、系统阻尼的情况下可以建立等效的振动模型,其最终结果类似于一个质点在二维空间中的振动。

力平衡模式要求系统振动轴的空间位置绑定,并且与测量的固定电极位置一致,需要利用负反馈回路去平衡因为哥氏力(即哥里奥利力)耦合导致的从振轴y 轴的位移,在理想情况下,主从轴的运动轨迹类比于二维振荡器,主从轴方向的位移幅值变化,相对于质点的位移变化来说是一个慢变量,分析周期性振动系统的控制算法采用平均法(Averaging)。在一个半球谐振子的谐振周期内,可以认为慢变量的值基本不变,椭圆的长半轴参数a和短半轴参数q保持恒定,长轴转动角度θ保持恒定。主从轴位移利用同向和正交向位移幅值Cx、Sx、Cy和Sy来表示,符合系统谐振频率的变化量主要由sin(ωt)和cos(ωt)来体现,两式结合可以得出Cx、Sx、Cy和Sy同样是慢变量。在力平衡模式下,系统通过解调哥氏力反馈项获得角速度输入信息,利用慢变量的运动轨迹方程和在力平衡模式下得到主从轴运动耦合状态空间方程[9-10]。

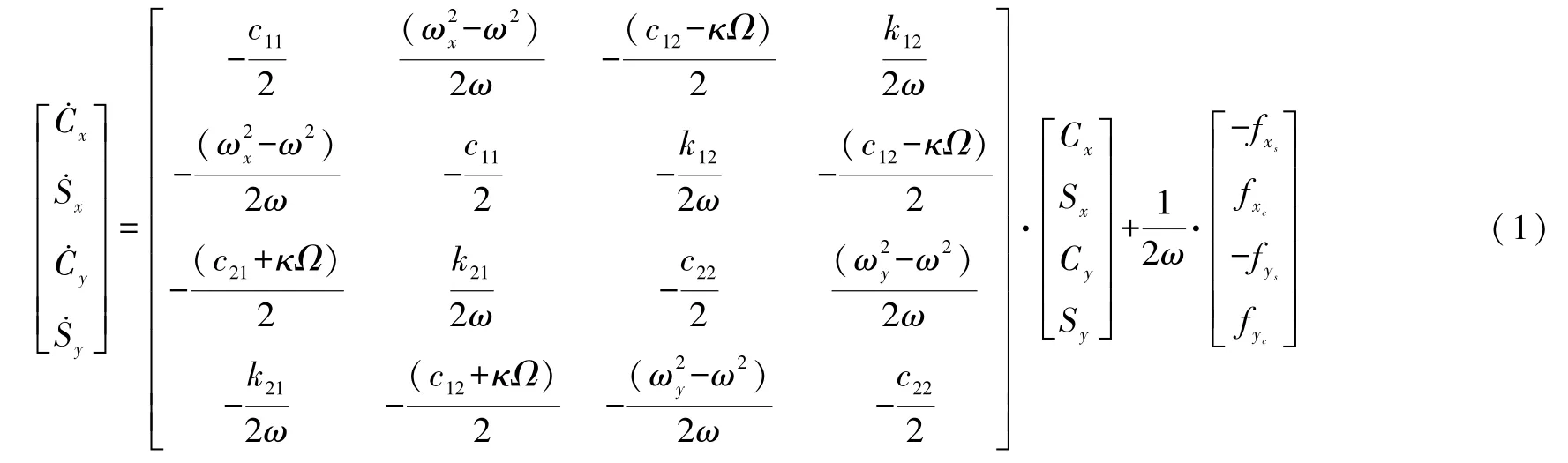
将系统内的快变量和慢变量分离,可以得到系统的针对慢变量的带有控制输入和耦合项的状态空间方程(1),由此得到系统负反馈控制回路示意图1。

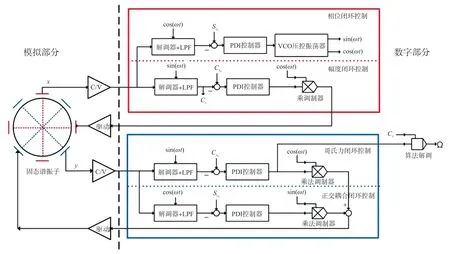
图1 负反馈控制回路示意图

(1)主轴幅度闭环控制:使谐振子等幅振荡。

(2)主轴相位闭环控制:控制相位关系,使系统工作在谐振频率点。

(3)从轴哥氏力闭环控制:平衡哥氏力振动项,可以得到系统的转动速率信息。此回路是实现控制系统输出动态响应优化的主要观察回路,通过实现哥氏力闭环控制的优化来优化对输入角速度的快速解析和准确分析。

(4)从轴耦合闭环控制:类比于从轴哥氏力控制,控制系统正交耦合误差,同样在深度负反馈的调节作用下可以有效地减少系统噪声,提高信噪比[11-12]。

力平衡模式下的控制框图如图2 所示。

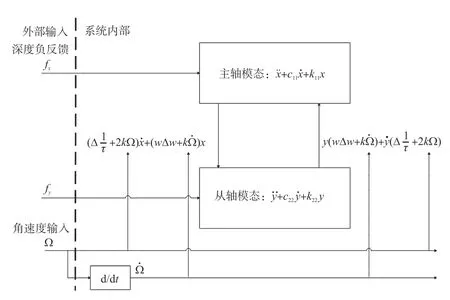
图2 力平衡模式控制框图

在主轴和从轴之间的耦合关系既包含系统内部的频率裂解和阻尼不均匀项,也受到外界输入角速度和角加速度的影响。对于系统主轴传递函数如式(2)所示:

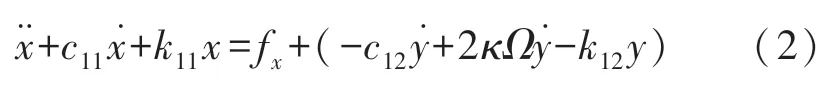
式中:x为等效主振型(主轴)位移；y为等效从振型(从轴)位移；k11为主轴刚度系数；fx为主轴控制力。

在力平衡模式下,系统稳定后从轴位移y和从轴速度都趋于零,因此在系统稳态分析时加以忽略。假设在深度反馈fx项作用下,主轴位移幅值稳定到系统预设量Cx0,稳定后的系统主轴位移为:

解析控制方程,假设得到的稳定后系统主轴幅值控制输入为:

下面分析主轴耦合项对从轴运动学方程的影响,在开环控制下研究从轴位移输出和主轴与外界输入角速度的关系,将主轴的位移x代入到开环的从轴传递函数方程中:

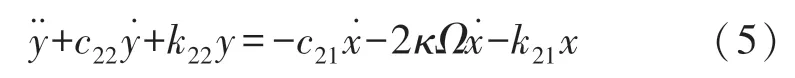
假设得到从轴位移的稳态解如式(6)所示:

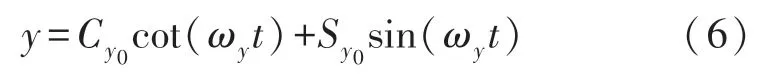
式中:

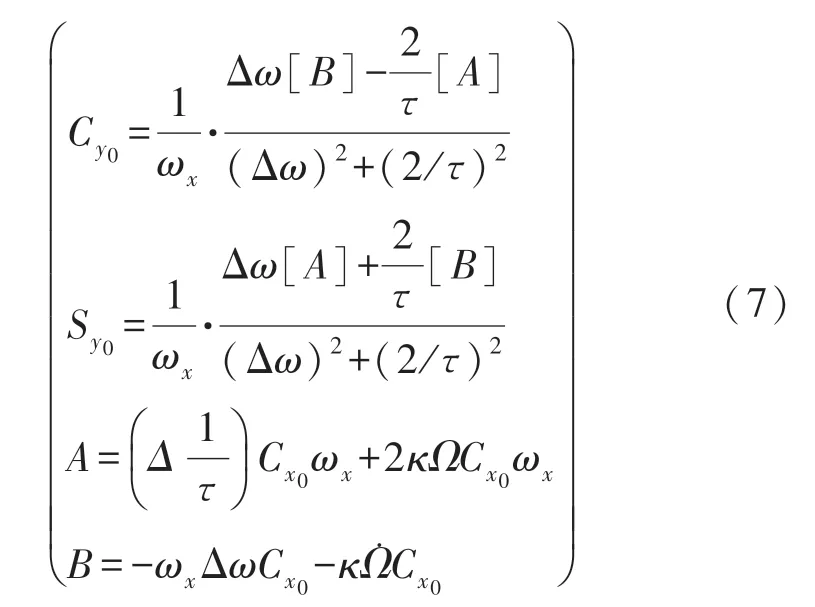
式中:Δω为谐振子频率裂解项；为谐振子阻尼项；为谐振子阻尼失衡项。

Cy0表示与主轴位移同相的从轴输出分量,Sy0表示与主轴位移正交项的从轴输出分量,从结果可以看出,两者的输出表达式中都包含了外界输入的角速度信息,同时两者的输出都受到了哥氏力项的影响,但是两者的影响系数不同。在方程式中:A∝·Cx0,B∝·Cx0,A和B表征的是结合系统外部输入的耦合项的影响,它们的实际作用效果,还受到前部系数的决定,观察方程可以得到耦合项系数只和系统内部参数有关,与外界输入无关,分别是陀螺仪频率裂解Δω和陀螺仪阻尼项2/τ。其中频率裂解项主要受到陀螺仪加工工艺水平和陀螺仪使用过程中的温度和老化影响,现阶段一般通过静平衡方式去削弱；当Δω=0 时,可以发现系统从轴的开环输出达到最大值,并且中主要包含哥氏力耦合项的动态响应,而正交耦合项也大大减小；在实际情况下因为Δω项的存在,系统的耦合项会对在主轴和从轴之间的输出产生干扰,从而控制结果受影响。

2 深度负反馈控制下的耦合PID 控制分析

2.1 PID 参数控制分析

2.1.1 锁相环控制回路

PLL 控制回路的目的是利用解调后得到的相位信息,通过相位信息为零来保证系统工作在其谐振频率上[8]。根据之前的系统控制框图,在经过解调器和低通滤波器之后,PID 控制输入为式(8):

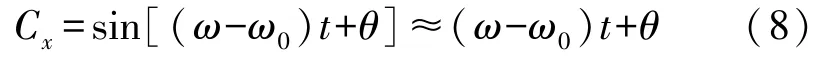
式中:ω表示主轴输出信号频率,ω0表示压控振荡器输出信号频率,在认为两者之间相差为小量的情况下,θ为系统相位差,可以线性化处理。压控振荡器(Voltage-Controlled Oscillator,VCO)经过陀螺仪系统和解调器与低通滤波器之后等效传递函数为式(9):

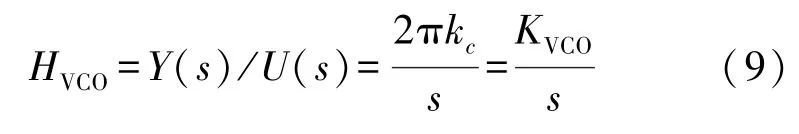
式中:kc为压控振荡器灵敏度。

该系统排除了陀螺仪之间的耦合信息影响,得到的闭环系统的传递函数为式(10):

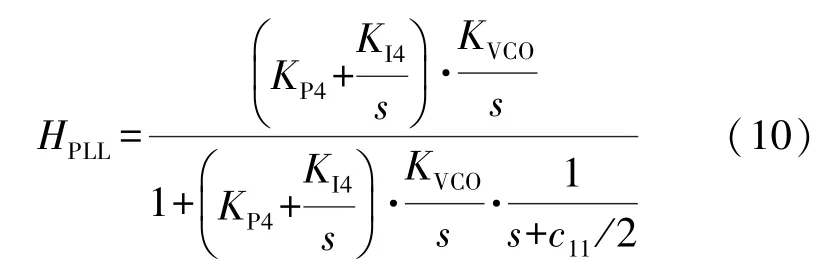
式中:KP4为PLL 回路PID 控制器比例系数；KI4为PLL 回路PID 控制器积分系数；KVCO为压控振荡器放大系数。

由此计算得到合适的PLL 回路的PID 控制参数值,达到系统的控制要求。

2.1.2 利用传统PID 整定方法确定

传统PID 参数整定,通过临界比例法或衰竭比例法来确定。2 种工程主要方法实际上都是一种经验控制方法,需要在人工干预的情况下做出大量的实验,并且最终的控制结果不可完全理想。传统的分析方法对于深地或太空等输入速率较小、系统带宽不高、控制速度要求较低的任务来说是合适的,但是对于类似于大机动平台的转速控制和快速稳定,则要求优化系统动态响应的稳定时间、调节时间、超调量等参数。

陀螺仪模型的参数设计如下:系统谐振频率为6 000 Hz,系统的频率裂解为0.05 Hz,系统的品质因子为3×104,根据公式得到系统的阻尼系数为1.25,在此仿真基础上,查看PID 耦合控制下的相互影响。

首先通过传统的临界比例法得到实现工程意义上得以控制的PID 控制参数,以此参数为基准值,研究某一参数变化对哥氏力闭环回路输出的动态响应的影响。参数的变化范围和参数的基准值有关系,选取某一维参数基础值的15%为变化量度,使它在40%到160%之间变化,观察对实验结果的影响。查看在模拟环境中,系统控制策略对从轴哥氏力闭环输出的影响是否线性或者可拟合,MATLAB 模拟结果如图3 所示。

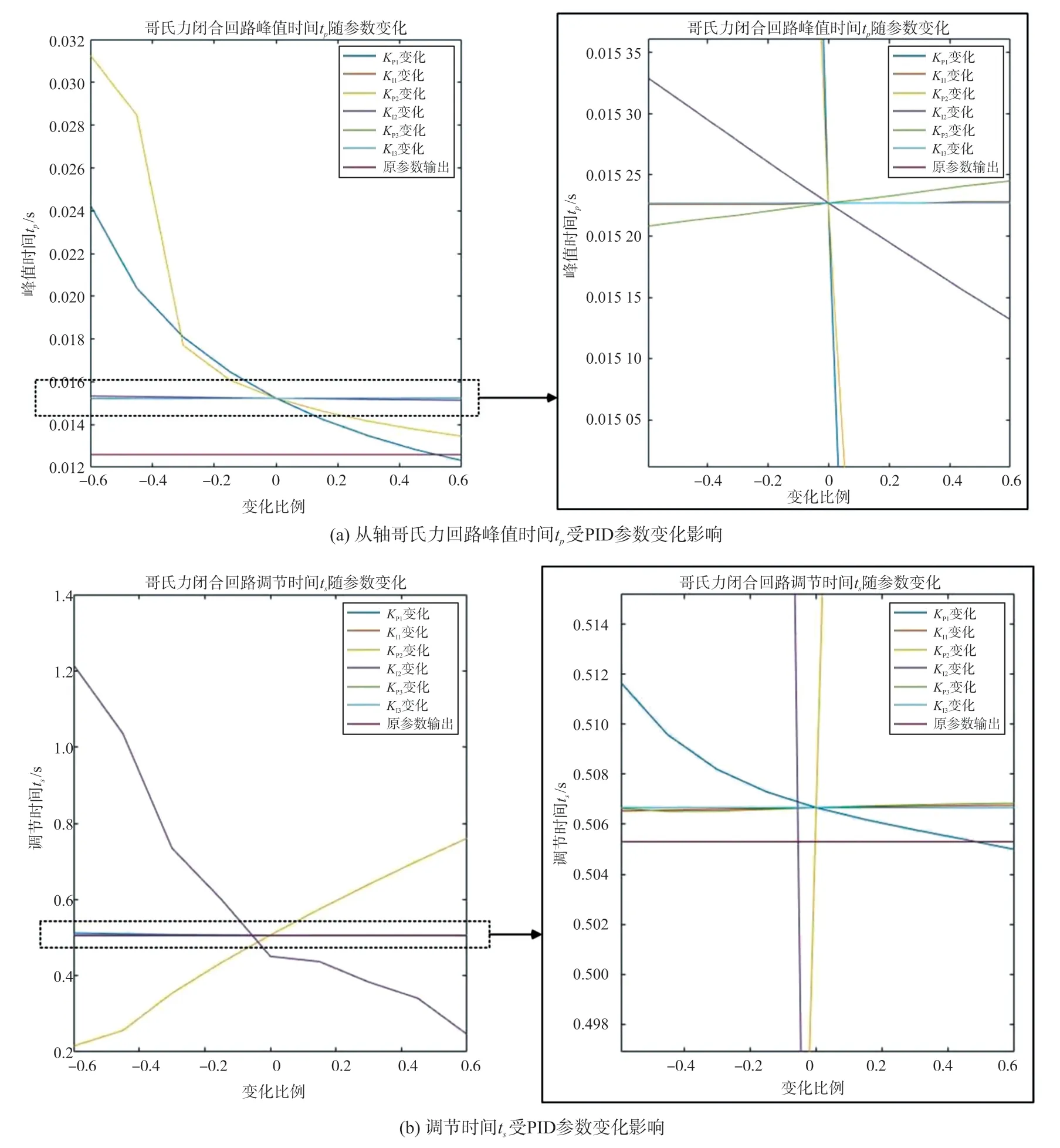
图3

从轴哥氏力控制回路结果受到各路参数的影响较大,从控制结果上并找不到明显的控制规律；PID参数变化对动态响应峰值时间tp和调节时间ts的影响是负相关,两个时间的表达不在同一量级,参数变化不能直接比较。因此在参数单一变化的情况下,不能使用解析或者拟合模型的方式得到最优化的控制参数。

2.2 去耦合项情况下分析PID 控制参数

在去掉系统耦合的情况下,得到PID 控制下的主轴幅值控制回路传递函数HCx、从轴哥氏力闭环回路传递函数HCy和从轴正交耦合闭环回路传递函数HSy为式(11):

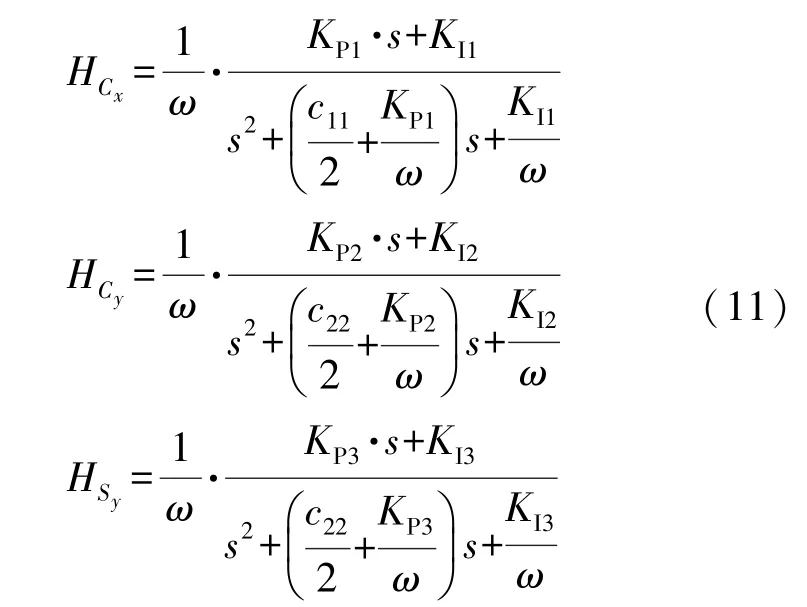
式中:KP1为主轴幅值控制回路PID 控制器的比例系数；KI1为主轴幅值控制回路PID 控制器的积分系数；KP2为从轴哥氏力闭环回路PID 控制器的比例系数；KI2为从轴哥氏力闭环回路PID 控制器的积分系数；KP3为从轴正交耦合闭环回路PID 控制器的比例系数；KI3为从轴正交耦合闭环回路PID 控制器的积分系数。

根据系统的带宽要求,系统拥有较高的带宽时,系统响应的快速性得以保障,能够很好地追踪到原信号并保持较大的稳态幅值,但是过高的带宽设计会使得高频噪声和干扰被放大,所以在系统设计时首先要保证系统响应的快速性要求,其次要考虑的是低噪声与抗干扰。按照系统目标要求设计负反馈回路的带宽约为300 Hz～400 Hz,去耦合之后的系统传递函数为二阶系统,当设置控制参数使系统阻尼比为0.707时,系统的动态响应优化。利用去耦合的传递函数解析可以得到合适的控制参数来满足带宽和阻尼比要求。通过此种方法可以得到系统的一套控制参数,得到主轴幅值控制回路、从轴哥氏力闭环回路和从轴正交耦合闭环回路的带宽分别是310 Hz、333.7 Hz 和312.3 Hz,且阻尼比在0.707 附近。

利用Simulink 建立模型,将控制参数代入到去耦合系统和实际耦合系统得到的输出结果比较如图4 所示。

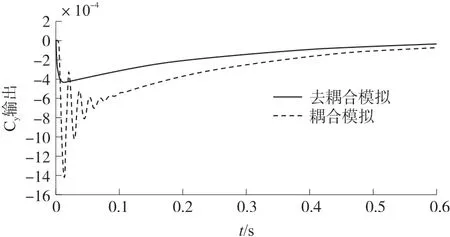
图4 Simulink 模拟去耦合和耦合输出比较

相比较去耦合情况,真实模型下的回路输出的超调量更大,系统响应的快速性降低,带宽有所减小；由比较结果可以看出在去耦合情况下得到的满足带宽要求的控制参数,在真实的耦合系统中可能无法达到最终的要求,耦合项的存在对系统的动态响应的影响就较大。

最终实现的控制效果由从轴哥氏力控制回路的输出表征,在考虑系统的动态响应时主要是考虑到系统输出的超调量σ和调节时间ts,引入误差积方法(ITAE 方法)[13],利用对系统时间t和系统误差绝对值｜e(t)｜乘积的积分,得到系统误差曲线在时间加权下包围面积,面积越小,则系统的输出的调节时间和超调量的综合考虑越佳,通过减小此数值可以降低系统输出表征值,系统的最终输出是通过哥氏力回路的反馈量解析得到系统的角速率输入信息,因此最终系统的优化目标为优化哥氏力闭环回路的动态响应。函数表达式如式(12):

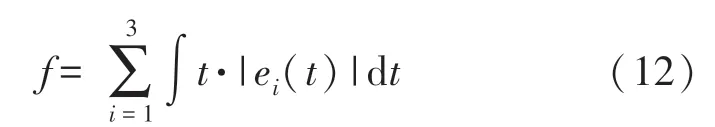
经过计算得到在去耦合系统中设计的优化控制参数值,在耦合系统下控制输出的ITAE 数值为49.83。

3 利用粒子群算法(PSO)优化PID 设计

3.1 粒子群算法(PSO)原理

由于传统的PID 参数调配方法适用于单个PID控制器且没有耦合作用的情况下,对于6 维甚至更高维度的控制参数不能做到有效的优化。粒子群优化算法(PSO)是在1995 年由Eberhart 博士和Kennedy博士一起提出,通过参考鸟类群体寻找食物的方法,目标函数的最优值,鸟类在寻找食物时,在每一次发现食物时都会对食物的质量和数量做出判断,并且根据当前的移动方向和过去游历路径上食物品质最好的方向来改变接下来的移动路径,并且在鸟类群体间还有信息的交流,它们通过其它鸟类寻找到的最佳的食物地点来更改自己的移动方向。由此就诞生出了粒子群算法,通过粒子进行全局寻优,是一种基于群体间协作、信息共享的搜索算法[14]。粒子群算法的计算步骤如图5 所示。

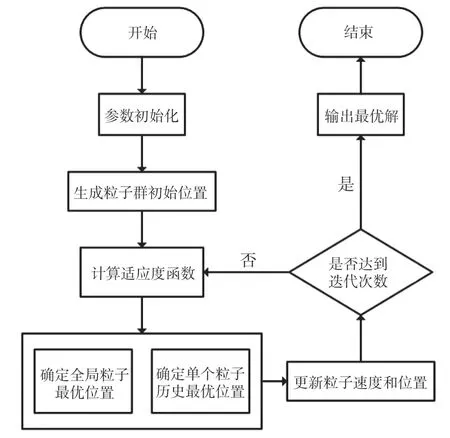
图5 粒子群算法流程图

确定粒子群算法的各个参数的设定,包括参数维度N、参数初始范围(Xmin,Xmax)、粒子群算法中的两个惯性系数(c1,c2)、种群规模M和迭代次数n。参数维度是指要优化参数的个数；参数初始范围是在预知的最优解的大致范围内,取得参数的初始分布；惯性系数代表了粒子速度迭代对历史最优位置与历史速度的依赖程度,决定算法拟合速度和收敛性；迭代次数由系统要求精度确定,太小达到不了预期结果,太大浪费计算仿真时间。

参数的初始设置是随机的,要求在预设置范围之内:x=(x1,x2,…xN),其中xi∈(xmin,xmax)…,i=1,2,3,…,N。每个粒子的初始速度设为0,第j个粒子的下一次速度的计算由3 部分组成,如式(13)所示:

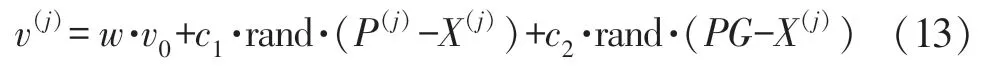
式中:w代表速度惯性系数；c1和c2代表最优位置惯性系数,也叫做学习因子。v0表示粒子上一次的速度,P(j)表示第j个粒子历史自适应度最高的位置,PG表示全部粒子在历史上自适应度最高的位置。

第j个粒子的下一次的位置和上一次位置与计算速度的关系如式(14)所示:

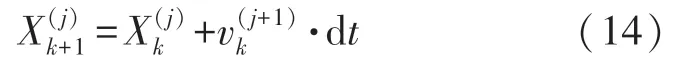
dt为仿真间隔,控制仿真的优化速度,通常可以设为1。设计自适应度计算方法F(P(j))和F(PG),实时更新各个粒子和全局的最优位置。

3.2 利用粒子群算法实现PID 参数优化

在目前搭建好的陀螺仪仿真系统中,一共有6个参数需要被优化处理,分别是KP1、KP2、KP3、KI1、KI2和KI3,适应度函数的设置采取ITAE 方法,参数设置如下:种群规模M=15,学习因子c1和c2都设置为2,迭代次数设置30,惯性系数w设置为1。在适应度函数要求下一次性优化全部参数,这样可以在系统的优化过程中,综合考虑到系统的耦合作用影响,得到的优化结果如图6。

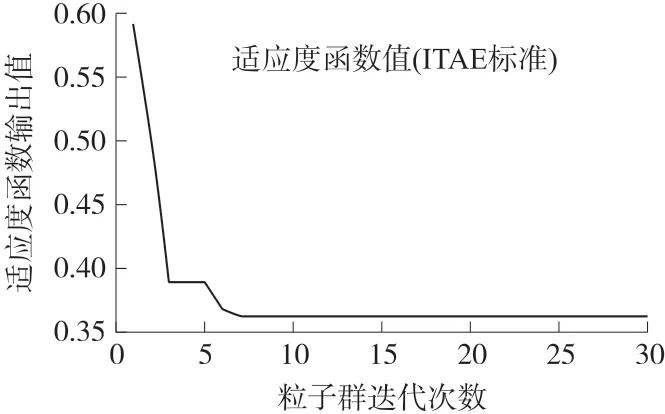
图6 适应度函数值随迭代次数变化

适应度函数最终优化数值ffin=0.362 6。将传统的参数整定方法和PSO 参数整定法进行比较,2 种控制参数设计方案模拟后得到的哥氏力控制回路的系统输出比对如图7 和表1 所示。

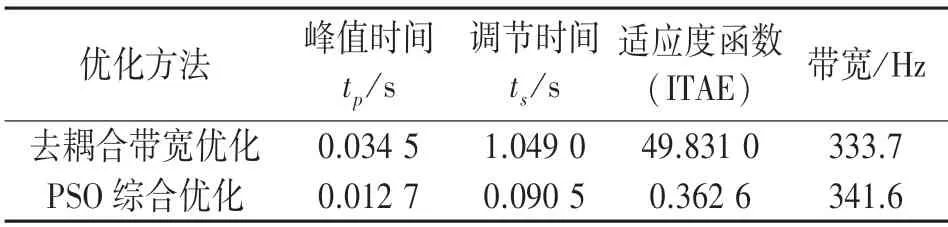
表1 两种优化的Cy 输出结果比较

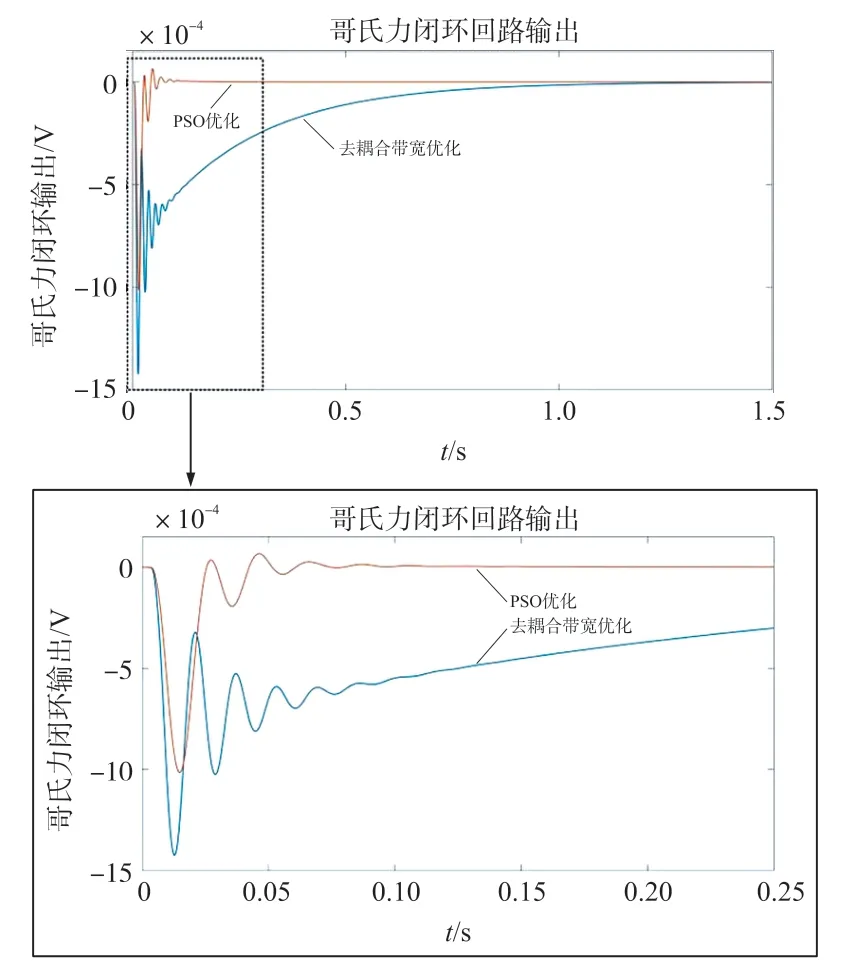
图7 两种方案哥氏力闭环输出时序输出比较

由表1 可以看出,2 种设计方法的带宽均在340 Hz 左右,不会因为过大的带宽而增加系统噪声的处理压力,但是利用PSO 优化得到的控制系统拥有更加优秀的动态响应过程；经过2 种方法比较在利用PSO 优化时既可以满足系统的带宽需求,也可以更加优化系统的动态响应过程。

4 结论

在陀螺仪控制系统中,系统主轴和从轴之间存在着耦合关系,在只考虑系统的静态误差时,这种耦合关系并不会对控制参数造成什么影响,只要可以完成控制,系统在一定时间里都可以趋于稳定。但是由于主轴系统和从轴系统的耦合关系的存在,在分析系统的动态响应时,不能通过去耦合的方式代替原有系统,利用去耦合的系统带宽设计出来控制参数的实际控制效果和去耦合模拟得到的效果有很大的差别。在控制参数和实际输出效果之间没有明确相关对应关系,并不能通过拟合方式得到最优的控制参数。粒子群算法(PSO 方法)可以代替基于大量人工调试的传统的PID 参数整定方法,相比较传统的利用带宽要求优化PID 控制参数,通过ITAE 准则对系统输出的动态响应问题做出量化,在动态响应的超调量、峰值时间和调节时间之间做出最优选择。对于陀螺仪动态响应的控制优化,利用粒子群算法做综合控制优化,既能考虑耦合量优化,也可以缩减优化时间,是更为出色的控制优化方案。