非对称式双层LC 谐振结构的无线无源柔性压力传感器设计*

秦国轩，杨 林，娄文涛，董和磊，于仕辉*

(1.天津大学微电子学院,天津 300072；2.中北大学仪器与电子学院,山西 太原 030051)

柔性压力传感器具有体积小,灵敏度高,可承受形变大等特点,在电子皮肤,医疗检测以及可穿戴设备等领域得到广泛应用[1-5]。传统的电容式柔性压力传感器都是采用有源结构,导致其在实际应用中存在工作效率低、维护成本高以及能耗大等问题[6-7]。而无线无源的设计可避免当前传感器的缺点,从而提高传感器的品质。LC 谐振结构具有无需物理接触便可获取信息的特点,为实现无接触式传感器提供一种选择。同时,LC 结构拥有体积小、成本低、使用寿命长且无需内置电池的优势[8-12],因此,LC 谐振结构的无源无线传感器受到了广泛关注。但是该类传感器的灵敏度较低,为提高柔性压力传感器的灵敏度,通常采用在柔性衬底上加入微结构等设计[13],工艺复杂[14]。提出了一种新型的非对称式双层LC 结构传感器设计,仅需在柔性基底两侧印制平面环形电感,两层电感之间通过电磁耦合即可产生联系,无需通孔操作,工艺简单有效。而且该结构可以有效降低传感器的初始谐振频率,提高谐振回路的品质因子,增加柔性压力的传感器的相对灵敏度。

1 基于LC 谐振传感器机理以及提出新型结构模型

基于单层LC 谐振的无线无源柔性压力传感系统由柔性基底上的谐振器以及读出线圈组成。当柔性衬底上受到的压力变化时,会使得LC 谐振器的谐振频率随着受到压力的变化而变化。当读出线圈上的扫频信号与谐振器的谐振频率相等时,可以从网络分析仪中读取阻抗特征曲线或输入回波损耗得知谐振传感器的谐振频率变化,从而推算出柔性衬底上受到的压力大小。

单层LC 谐振的无线无源传感器的等效集总电路模型如图1 所示,根据基尔霍夫定律,读出线圈端口与LC 谐振器端的电压与电流关系分别满足

图1 单层LC 谐振集总电路模型

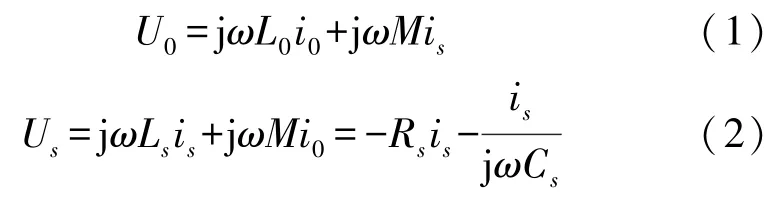
式中:U0,Us,i0,is,L0,Ls,Cs的定义如图所示,M为谐振器与读出线圈之间的互感系数,计算公式如下,其中k为耦合系数。

当外部读出线圈靠近螺旋电感与传感器发生磁耦合时,读出线圈的等效输入阻抗Zin可以表达为

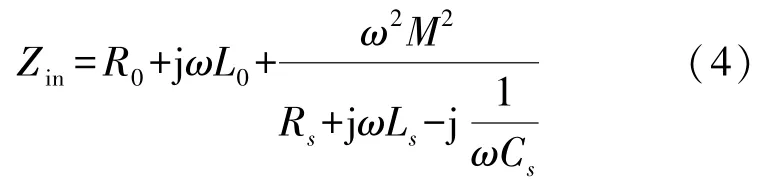
式中:ω为角频率,Ls,Cs,Rs分别是LC 谐振器的等效电感,等效电容和等效电阻。谐振频率fs以及品质因子Q的计算公式为

将其代入式(4),则输入阻抗的虚部,实部以及相位角计算公式可以分别表示为

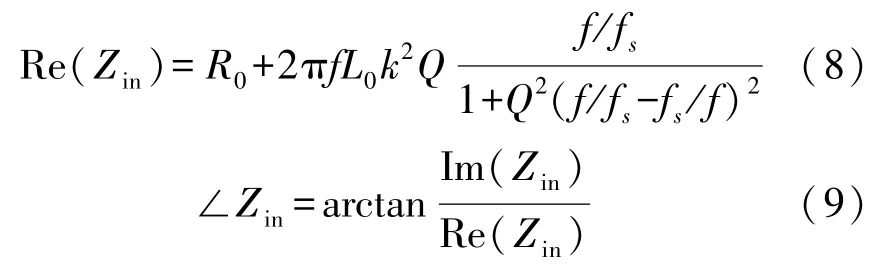
输入回波损耗S11参数可以表示为

LC 谐振器采用平面螺旋电感,主要包含电容,电感和电阻3 个基本参数。矩形平面螺旋结构的电感理论值可以用经典计算公式

式中:N是线圈的匝数,davg=(din＋dout)/2 为平均直径,ρ=(dout-din)/(din＋dout)为填充率,μ为磁导率,K1和K2可以分别取值为2.34 和2.75。平面螺旋电感的电容参数主要包括一般平行板结构电容以及寄生电容。平行板电容的基本计算公式为

式中:A为两平板正对面积,D为两平板间的间距,εr为相对介电常数,ε0=8.85×10-12F/m。根据简化模型,平面矩形螺旋电感的每单位长度电容理论计算值可以表示为

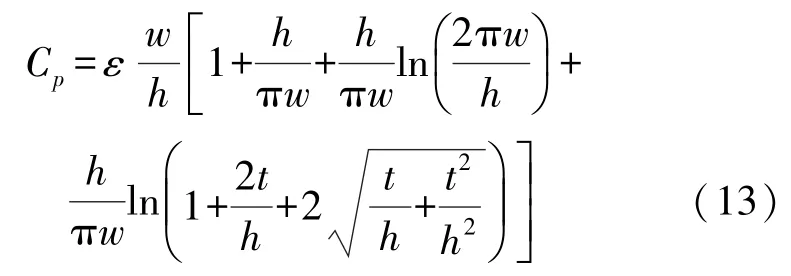
式中:ε为介电常数,t,w,h分别为极板的厚度,宽度以及极板间距离的一半。由于等角映射,该方程式中的边缘效应仅限于二维。当极板长度远远大于极板宽度时,沿拐角处的边缘被省略,因此该方程式可以近似表达电容大小。

将式(12)进行推导可以得到

根据式(14),改变介电常数和两极板面积时,均可使电容发生线性变化。但是相比于改变极板间间距引起的电容非线性变化,更容易实现。当基板采用柔性衬底时,更容易通过压力来改变极板间的间距,充分说明在柔性基板上搭建螺旋环绕电感充当谐振器,构成无线无源柔性压力传感器的可行性。

非对称式双层结构以及对称式双层结构如图2(a)所示。两层电感都可采用印刷的方式在柔性基底上实现,并不需要打孔工艺。非对称式双层结构柔性基底上侧的平面螺旋电感采用由内向外的顺时针绕向,基底下侧的螺旋电感采用由内向外的逆时针绕向,即与上层环形电感相反绕向。当读出线圈靠近LC 谐振回路时,谐振器由于双层电感的旋绕方向不同而形成与传统单层结构相比不同的感应电流方向,同时谐振器与读出线圈之间的互感系数也会发生改变,由此会改变读取线圈的特征频率fs,输入阻抗Zin以及品质因子Q等。而双层同轴同绕向的对称式结构,并不能产生与单层结构不同的感应电流方向,与传统单层结构差异不大。在此基础上提出非对称式双层结构的集成电路模型如图2(b)所示。其中CS1,CS2,RS1,RS2,LS1,LS2分别为上层平面螺旋电感与下层平面螺旋电感的等效电容,等效电阻与等效电感,C0为两电感之间平板电容。其中忽略了部分寄生电容,在考虑2 个等效电感LS1与LS2之间会产生互感的同时,将外部读出线圈对它们的电磁耦合也包括在内。设计中的矩形平面螺旋电感的结构如图2(c)所示,其中的具体参数如表1 所示。

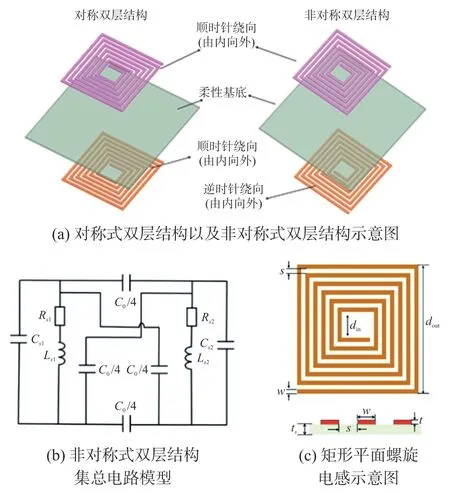
图2

表1 LC 谐振器的基本参数设计

2 仿真结构分析

为了验证集总模型的双层非对称式LC 谐振结构无线无源柔性压力传感器设计的可行性,确定双层电感之间的电磁耦合对传感器性能的影响以及等效电路的正确性。首先采用SPICE 电路仿真软件验证集总电路模型的可行性,随后采用HFSS 电磁仿真软件分析,将该结构与对称双层LC 结构和单层LC 进行对比,比较非对称式双层结构的差异。

2.1 电路仿真

由于螺旋电感本身的复杂性以及双层螺旋电感带来更多的寄生效应,将电路理论值进行了适当的估算。根据式(11)以及式(13),近似计算出平面螺旋电感的理论值,其中计算出的平板电容值C0的理论计算值为17.5 pF,单层电感值LS1以及LS2的理论计算值为3.569 mH。将计算值代入SPICE 建立的集总电路模型中,仿真结果如图3 所示。可以看出输入阻抗的相位在29.4 MHz 时达到最低值。通过输入阻抗相位的不同,可以读出非对称式双层结构的谐振频率点。通过将式(9)进行偏微分=0操作,即可求导出阻抗相位变化到最低点时的频率fphase-dip,推导出的阻抗相位最小发生频率为

图3 利用SPICE 电路仿真结果图

当耦合系数k较小时,fphase-dip可以近似看成谐振频率fs。其中可近似认为相位最低值时对应的频率即为谐振频率,所以非对称式双层结构的集总电路模型具有可行性。

2.2 感应电流仿真

根据楞次定律,感应电流的磁场总要阻碍引起感应电流的磁通量的变化。当读出线圈靠近带有LC 谐振结构的柔性基底时,在平面螺旋电感中,会产生相应的感应电流阻碍磁通量的变化。源于非对称式双层结构特定的旋绕方向,其中平面螺旋电感内产生的感应电流方向会与单层结构产生很大的不同,如图4 所示。单层LC 结构中,从上往下看电流方向为顺时针流向。在非对称双层结构中,从上往下看上层螺旋电感内电流方向的总体趋势为逆时针流向。在非对称式双层螺旋结构中由于下层存在不同绕向的平面螺旋电感,两电感感应出极性相反的磁场,产生了不同方向的感应电流,这也影响电感之间的耦合程度以及阻抗特性。

图4

2.4 输入阻抗仿真

(1)阻抗实部

一般情况下,特征频率fs也可以从观测阻抗实部的最大值处的频率获得。通过式(8)可以推导出

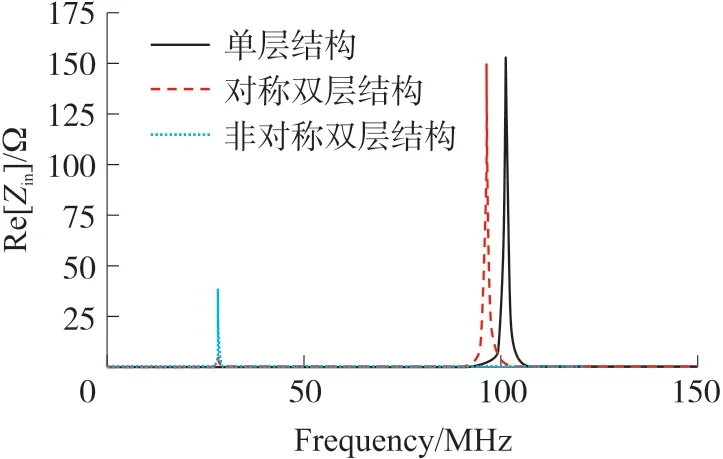
图5 3 种结构下阻抗实部仿真对比图

根据3 种结构的阻抗实部最大值对应的频率可以读出,非对称双层结构的fmax(Re)=27.8 MHz,对称式双层结构的fmax(Re)=98.8 MHz,单层结构的fmax(Re)=100.1 MHz。非对称结构的阻抗实部值与其他两者结构的阻抗实部值存在较大差别。非对称双层结构的阻抗实部值为27.9 Ω,与对称双层结构的147.6 Ω 以及单层结构的153.1 Ω 相差很大。通过式(5)可以看出影响阻抗实部大小的值包括品质因子,耦合系数等。其中因为耦合系数为平方项,且耦合系数的取值范围为0～1,其为主要影响因素。非对称结构由于更小的耦合系数,从而得到更小的阻抗实部值。

(2)阻抗幅值

因为｜Zin｜2=(Rezin)2＋(Imzin)2,阻抗实部的大小也必然影响着阻抗幅值的大小。仿真的3 种结构的输入阻抗幅值仿真对比图如图6 所示。单层结构以及对称式双层结构的输入阻抗幅值差距不大,分别为157 Ω 和153 Ω。而非对称双层结构幅值则只有27 Ω,明显远远低于其他两种结构。根据输入阻抗表达式进行微积分处理可以得到

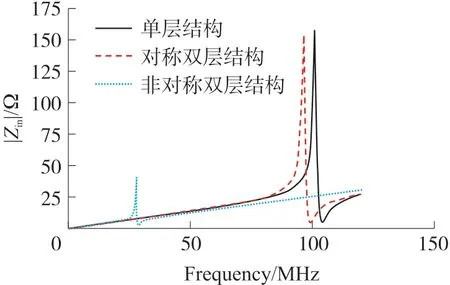
图6 阻抗模值对比图

从式(17)中可以看出耦合系数同样对阻抗幅值的影响很明显。非对称式双层结构在改变读出线圈与谐振器之间耦合系数的同时,也将输出结果中输入阻抗的幅值降低了。

2.5 相对灵敏度仿真

由于非对称式双层结构中读出线圈与谐振回路之间的耦合系数较小,且根据耦合系数对阻抗相位的影响较大,利用非对称式双层结构的柔性压力传感器将有着更大的相对灵敏度。

(1)仿真柔性基底厚度变化带来的影响

当谐振结构应用于柔性基底上时,柔性基底受到压力的作用而产生形变,基底的厚度会随着压力增大而减小,所以仿真基底厚度对谐振频率的影响可以近似表示谐振柔性压力传感器对所受到的压力时谐振频率的变化。非对称双层结构以及对称式双层的仿真结果如图7 所示。

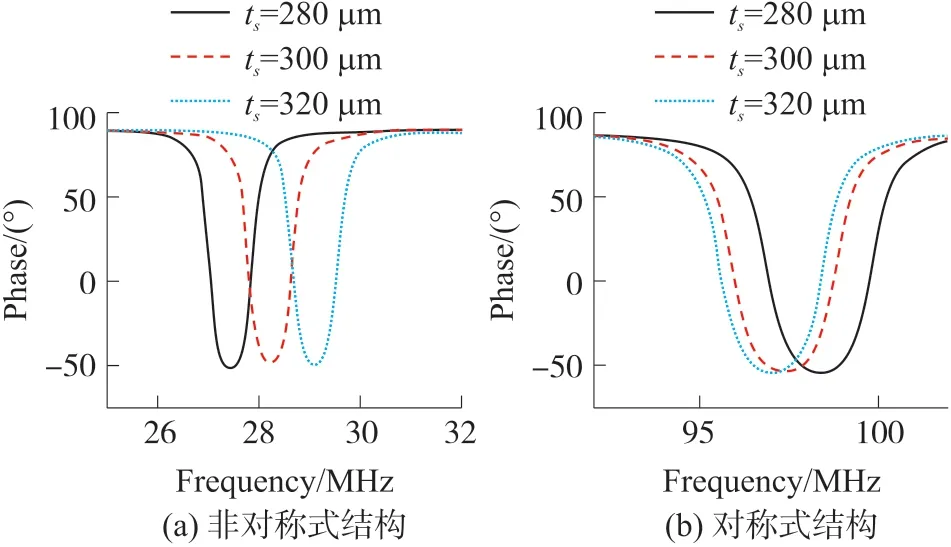
图7 阻抗相位随基底厚度变化

从图7(a)中可以看出,在非对称双层结构中,当柔性基底厚度分别为320 μm,300 μm 和280 μm 时,谐振频率点的仿真结果分别为29.1 MHz,28.2 MHz和27.4 MHz。谐振频率随着基底厚度的增大而增大。而双层对称结构仿真结果如图7(b)所示,当柔性基底厚度分别为320 μm,300 μm 和280 μm 时,分别为96.9 MHz,97.4 MHz 和98.4 MHz。谐振频率随着基底厚度的增大而减小。从柔性基底受压力形变的角度看,非对称结构的相对灵敏度为5.8%,对称双层结构的灵敏度为1.5%,非对称式结构将相对灵敏度提高了4.3%。

(2)仿真平面螺旋电感的外径变化带来的影响

当非对称双层结构应用于柔性压力传感器上时,不仅会产生向下的压力,同时会有左右方向的受力。这时左右方向的受力便会改变环形电感的外径,可近似类比柔性基底受水平方向的力对谐振点的影响。非对称双层结构与对称式双层结构谐振频率随环形电感的外径变化如图8 所示。当外径从26 mm 变到30 mm 时,非对称双层结构的谐振频率从35.25 MHz 减小为27.81 MHz,相对灵敏度为21.1%。对称式双层结构的谐振频率则是从112.53 MHz 减小为96.49 MHz,相对灵敏度为14.5%。非对称式双层结构的相对灵敏度比对称式结构增加了6.6%。从变化趋势看到,两者的谐振频率会随着外径的增大而减小。根据式(11),平面螺旋结构的电感理论值与平均直径成正比,与填充率成反比。在内径不变的情况下,而随着外径增大,平均直径增大,填充率明显减小,使得电感增大,从而谐振频率点会随着外径的增大而减小。由于无论单层结构还是双层结构都不能改变矩形螺旋电感的电感变化趋势,所以两者结构的变化趋势都是随着外径增大,谐振频率随之减小。

图8 谐振频率随外径变化曲线

3 结论

提出了一种基于非对称式双层LC 谐振的无线无源柔性压力传感器设计,该双层设计采用印刷工艺,通过两层电感的相互耦合的方式实现联系,而避免了传统通孔工艺带来的实现难度。同时通过提出非对称式双层结构的集总电路模型,利用SPICE 和HFSS 软件分别对该结构进行电路以及电磁仿真。对比传统单层结构以及对称式双层结构,发现采用非对称式双层结构的柔性压力传感器,有效地降低了传统单层LC 谐振的初始频率,增大了谐振器的品质因子,同时将传感器的相对灵敏度提高了6.6%。该结构为未来无线无源传感器设计提供了一种新的设计思路,具有广阔的应用前景。