基于SVM与改进的NSGA-II算法的电磁式卷烟加热器多目标优化研究

魏信建， 李志强， 邹金慧， 李廷华， 尤俊衡， 王汝， 尚善斋

(1.昆明理工大学 信息工程与自动化学院， 云南 昆明 650500； 2.云南中烟工业有限责任公司 技术中心， 云南 昆明 650202)

近年来，随着人们对传统烟草制品危害性认识的增强以及全球许多国家公共场所禁烟意识的不断提高，一类具有降焦减害、不产生侧流烟气,且能在一定程度满足人们生理需求等特点的新型烟草制品正在烟草消费人群中迅速流行[1]。相对传统烟草制品而言，新型烟草制品类型繁多,并且随着社会技术发展创新不断增加，其中电加热卷烟作为当前市场上新型烟草制品的主流产品，具有“加热烟草而非燃烧烟草”的特点，利用电能在低温状态下(400 ℃以下)对烟草加热，有效避免了烟草材料在高温燃烧裂解过程中产生CO、焦油等有害成分[2]。电磁感应加热作为一种清洁环保的加热技术，因其非接触加热、热转化效率高等优点广泛应用于机械加工、冶金制造、家电等工业及生活领域，相较于其他的加热方式，具有一般传统加热无可比拟的优越性。

电磁式卷烟加热器在对特制烟支的加热过程中，相较常规的电阻加热方式具有热响应速度快、加热均匀、便于自动控制等优点。在消费者使用电磁式卷烟加热器进行抽吸体验时，在较短的时间内使烟支内部的烟草材料获得一个符合期望的目标温度,对消费者抽吸体验评价具有重要影响。电磁加热组件的电流频率、电流强度这些参数都对发热元件上的温度分布产生重大影响。目前市场上的烟具发热元件大多使用高磁导率金属材料制备，其发热过程与钢制材料感应加热过程相似。文献[3]利用ANSYS有限元软件研究了钢板感应加热过程中温度场分布，采用逐一控制参数的方式分析了电流频率、电流强度对钢板温度场分布的影响，并没考虑感应加热参数间相互耦合对结果的影响。文献[4]研究了电流密度和频率对钢绞线加热效果的影响，应用多目标遗传算法对这两个参数进行了优化，对每个子目标函数线性加权转换为单目标优化问题，其中权重取值机理不明。文献[5]基于人工神经网络与遗传算法对感应加热参数进行优化，利用感应加热参数与输出温度数据建立回归预测模型，并以回归预测模型为遗传算法中的适应度函数对感应加热参数优化，其仅对金属工件的温度这单一目标进行优化。

电磁式卷烟加热器是一个包括电磁场、温度场、电路的非线性耦合传热系统，其加热过程伴随着复杂的磁热耦合，是一个随时间变化的多元非线性函数，在不同感应加热参数下卷烟加热器的温度场分布不同，为了在加热器上获得理想的温度分布，对感应加热参数全局优化就显得十分重要。基于此，本文采用一种基于支持向量机(support vector machine，SVM)与改进的NSGA-II算法相结合的多目标遗传算法对感应加热参数进行全局优化，优化电磁式加热器的温度场分布特征。

1 烟具仿真模型与优化分析

1.1 建立仿真模型

电磁式卷烟加热器在硬件上主要由直流电源、逆变控制电路、电磁加热组件等部分组成，其工作原理如图1所示。采用双节串联锂电池作为直流电源，在振荡模块的逆变作用下电磁线圈中通入交变电流，会在铁磁性金属感应体周围产生高频交变磁场，变化的磁场使得金属感应体表面形成一层层涡流，在涡流热效应的作用下，金属感应体表面温度迅速升高，进而对烟草材料加热。

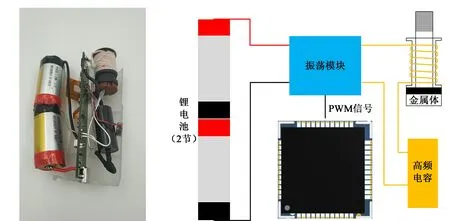
(a)样机实物图 (b)电路结构图 图1 电磁式卷烟加热器电路原理结构示意图

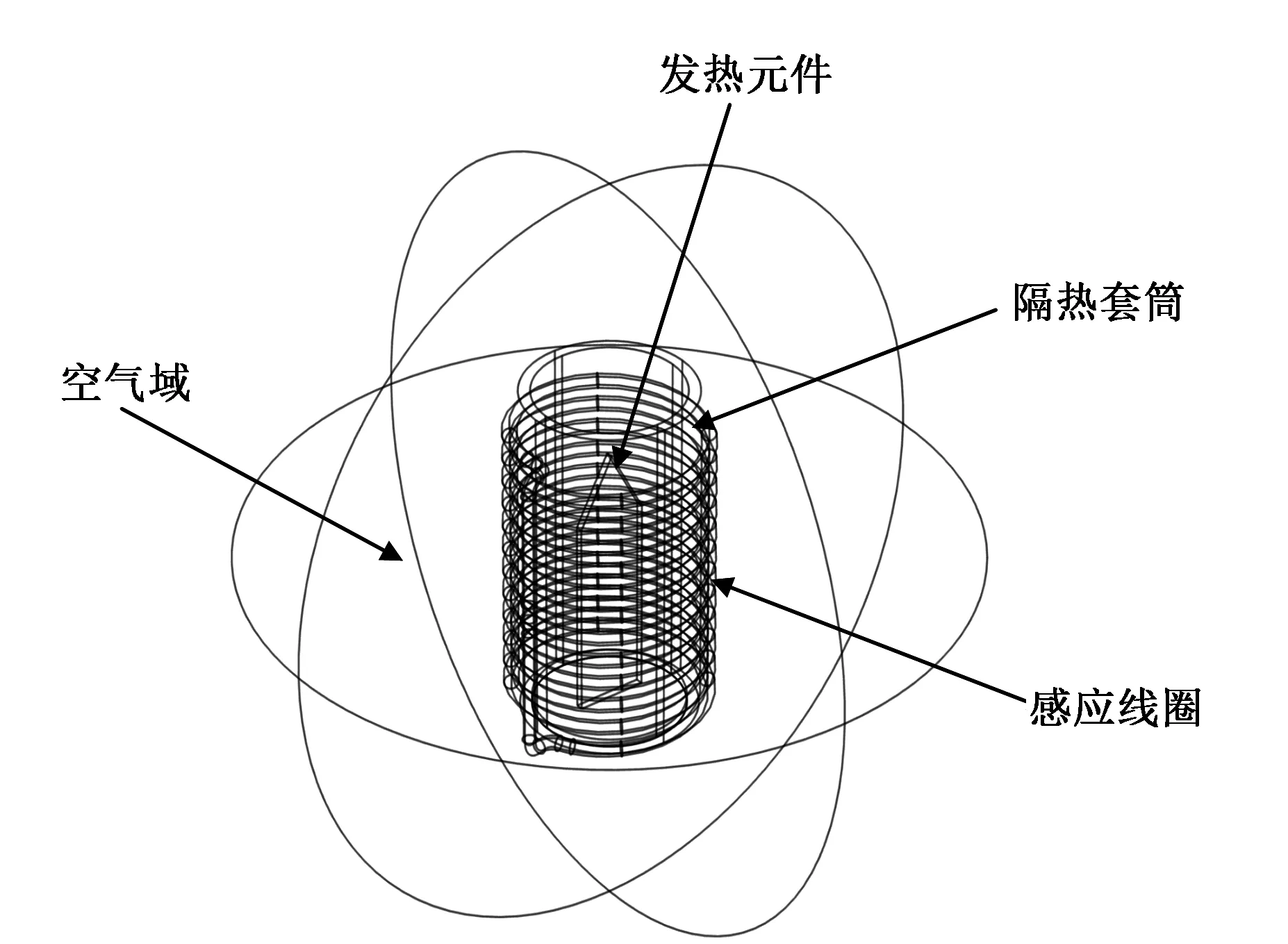
图2 烟具三维仿真模型

在电磁式卷烟加热器加热过程中，金属感应体上电磁场和温度场之间是相互影响的，感应涡流产生的电磁热作为内热源，经过热的传导会在计算域中产生一个温度分布。电磁加热组件作为电磁式卷烟加热器的核心部分，直接对烟草材料加热，其温度分布是影响卷烟烟气化学成分释放特性的重要因素，直接影响烟具产品整体性能和抽吸口感等。电磁式卷烟加热器磁热耦合模型求解域可简化为空气域、隔热套筒、感应线圈、发热元件4个部分组成，其几何模型如图2所示。发热元件外形为叶片刀状结构，方便烟支的插入，在其周向位置处设置有隔热套筒，由高温隔热材料PEEK制备，既作为烟支容纳腔，又可防止热量的流失，感应线圈螺旋缠绕在隔热套筒上。仿真模型各求解域的材料单元、几何尺寸见表1。

在已建立的模型上施加载荷激励，分别施加强度为range(1[A]，10[A]，1[A])、频率为range(40[kHz]，120[kHz]，10[kHz])的交变正弦电流，并对几何模型进行网格剖分。考虑到研究对象为发热元件上的温度场分布，该区域部分的网格划分需要较高的精度，因此在该区域采用细化网格。为了节省计算时间和保证整个电热单元上温度精度，在其他部分区域采用较细化网格。采用顺序耦合法对发热元件的瞬态电磁场和温度场求解，求解的终止时间为180 s，时间步长为1 s。通过对电流强度、频率进行参数扫描可以获得90组输入、输出数据，将这些数据用来训练SVM回归预测网络。

表1 几何模型材料单元及几何尺寸

1.2 烟具多目标优化问题分析

电磁式卷烟加热器的优化目标是在发热元件上获得一个稳定温度在(355±20) ℃范围的输出温度，保证发热元件上升时间尽可能小,从而令烟具的响应速度增快。因此针对性地选择了2个相关性较大的电气参数(电流强度I和频率f)作为优化变量。电磁式卷烟加热器多目标优化问题模型可表示为

minF1(X)=|T-355|， minF2(X)=t，

T=Svmpredict(X[I,f,t],model 1)，t=Svmpredict(X[I,f,t],model 2)，

s.t.∶ 1 A≤I≤10 A， 10 kHz≤f≤120 kHz，

式中F1(X)为输出温度函数，F2(X)为发热元件的上升时间函数，model 1、model 2是通过SVM回归模型得到的发热元件输出温度和上升时间回归模型。

电磁式卷烟加热器的多目标优化过程流程图如图3所示，步骤如下：

Step1:确定决策变量，建立烟具数学优化模型；

Step2:利用有限元仿真计算获得输入、输出数据以训练SVM，建立决策变量与各目标函数间的回归预测模型，同时以预测模型代替有限元的复杂计算，缩短了优化时间；

Step3:通过SVM学习所获得的回归预测模型输出作为NSGA-II算法的待优化目标函数，经过快速非支配排序、选择操作、遗传操作对种群进化，直至终止条件，获得最优的Pareto解集；

Step4:仿真验证优化的有效性。

图3 烟具多目标优化流程图

2 SVM回归模型建立及参数优化

电磁式卷烟加热器是一个包括电磁场、温度场、电路的非线性耦合传热系统，其加热过程伴随着复杂的磁热耦合，输入、输出之间存在高度非线性，难以确定可映射这种关系的函数表达式。因此，通过SVM对有限元模型计算获得的数据进行学习，建立发热元件输出温度及上升时间的回归预测模型。

2.1 SVM回归原理

SVM基于结构风险最小化原则，在寻找使整体结构化风险最小的过程中，泛化能力不断提高，同时使风险和置信达到最小，在小样本中，依然可以保持良好的回归能力。其本质是建立一个最优超平面作为决策曲面，使得正例和反例之间的隔离边缘最大化[6]。有限元仿真计算获得的数据量较少，属于小样本情况，用支持向量机可以进行良好的回归预测[7]。在非线性样本集{(x1,y1),(x2,y2),…,(xn,yn)}中，非线性超平面回归函数形式为

f(x)=ωTφ(x)+b，

(1)

式中ω为权系数向量，φ(x)为低维特征空间到高维特征空间的非线性映射，b为偏置。

回归估计函数f(x)在最小化ωTω/2时可取得较好的推广能力,引入松弛变量ζi，构建最优超平面，则优化函数可表示为

(2)

s.t.yi(ωTφ(x)+b)≥1-ζi，

ζi≥0，i=1,2,…,n，

式中C为约束惩罚因子。运用Lagrange乘子，同时引入核函数K(xi,xj)，得到SVM回归函数为

(3)

(4)

2.2 SVM回归模型的训练与测试

对核参数g=1/(2σ2)与惩罚因子C的优化是SVM研究中的重要问题，其取值的不同对输入样本训练获得的SVM模型泛化能力和分类性能具有很大影响。常规的SVM参数优化方法有实验法、网格搜索法、梯度下降法等。实验法步骤繁琐,过于依赖经验,缺乏理论指导；网格搜索法优化效果取决于两点间步长取值，当取值小时，优化效果好，但计算量大、十分耗时；梯度下降法对初始值的选择十分敏感。群智能算法在参数优化方面已经取得了较好的优化效果[8]，因此，本文在MATLAB平台下，运用LIBSVM工具箱分别采用遗传算法(genetic algorithm，GA)和粒子群算法(particle swarm optimization,PSO)对SVM参数优化[9]，对两者优化效果进行比较。LIBSVM工具箱训练的SVM模型结构为

model=svmtrain(trainy,trainx,option)，

(5)

[predict_y,mse,decision_value]=svmpredict(testy,testx,model)，

(6)

式中model为训练集训练获得的SVM模型，trainy为训练集标签，trainx为训练集属性，testy为测试集标签，testx为测试集属性，option为模型参数设置，predict_y为测试集的预测值，mse为均方误差。

本文将有限元模型计算获得的90组样本数据分为训练集和测试集，随机将70组样本数据作为训练集对SVM模型进行训练。对训练集和测试集进行归一化预处理后，分别运用GA和PSO算法对核参数g与惩罚因子C进行优化，并将优化后的参数导入到模型参数设置中，对SVM模型训练；最后在测试集上对训练获得的SVM模型预测精度进行验证，对比两种方法的参数优化效果，如图4、图5所示。

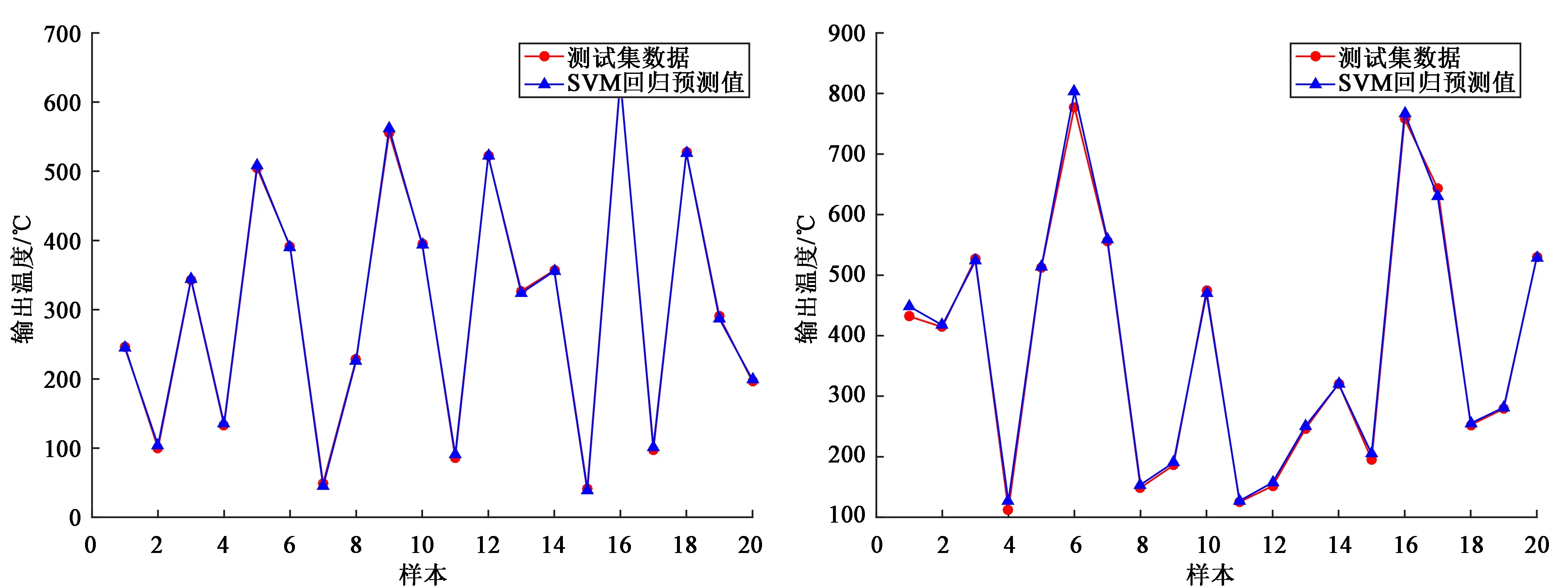
(a)GA-SVM输出温度模型 (b)PSO-SVM输出温度模型图4 GA-SVM与PSO-SVM输出温度回归预测结果与测试集数据对比

(a)GA-SVM上升时间模型 (b)PSO-SVM上升时间模型图5 GA-SVM与PSO-SVM上升时间回归预测结果与测试集数据对比

采用均方误差MSE和相关系数R2对不同参数优化算法模型进行评价，MSE值越小表示模型的预测精度高，R2值越大表示该模型的泛化能力越强。由表2可知，当采用GA对SVM参数优化时，输出温度与上升时间回归预测结果的均方误差MSE1=0.000 134，MSE2=0.007 986，相关系数R2分别为99.97%、98.78%，消耗时间约为50 s，与有限元仿真结果几乎无差异；当采用PSO对SVM参数优化时，输出温度与上升时间回归预测结果的均方误差MSE1=0.000 65，MSE2=0.011 5，相关系数R2分别为99.78%、98.10%，消耗时间约为30 s，与有限元仿真结果相差不大。由两者对比可以得出，利用GA优化的SVM输出温度及上升时间回归模型计算虽需要更长的时间，但回归模型的预测精度及泛化能力更优，因此采用GA对SVM回归模型进行参数优化。

表2 不同参数优化模型性能对比

3 NSGA-II烟具电磁参数优化

多目标优化问题即在不同约束条件下，同时处理若干相互矛盾的目标函数，这些目标函数间高度非线性并相互关联，很难求得各目标函数的最优解，因此，在求解多目标函数优化问题时，只有通过各目标函数间的折衷才能找到全局的均衡解，即Pareto解集[10-13]。在本文中电磁式卷烟加热器的多目标优化问题以电磁加热组件中发热元件的输出温度及上升时间为目标函数，通过GA-SVM回归模型中全局搜索电磁参数(I,f)获得输出温度在(355±20) ℃范围，且响应速度快(即上升时间短)的Pareto解集。

3.1 NSGA-II算法流程

NSGA-II算法将进化种群按支配关系分为若干层：第一层为进化群体的非支配个体集合；第二层为在进化种群中去掉第一层个体后所求得的非支配个体集合；第三层以此类推。选择操作根据个体所在层的大小即前沿值来进行选择，所在层越靠前被选择的优先级更高，处于同一层的个体则依靠拥挤度判断，直至个体数量到达种群规模设定值。然而，NSGA-II算法在一些方面仍然存在缺陷，例如在面对复杂度较高的目标函数时，其运行效率不高、精度较低[14-15]。

本文提出一种改进的NSGA-II算法来提升算法的运算速率和效率，在遗传过程中，其交叉概率算子服从正态分布，且变异概率会随着种群个体适应度评价函数自适应调整，在尽可能丰富种群多样性的同时，最大限度地保持种群个体的优良基因。

(1)引入正态分布交叉算子

传统的交叉算子在种群进化过程中，双亲都是以固定的概率在个体间实现信息的交换，这使得个体只能在一个较小的搜索空间进行求解，采样空间较小，所获得的Pareto解集很容易陷入局部最优，因此可对传统交叉算子加以改进。对种群个体进行实数编码，假设在种群中有父代个体p1与p2，经过正态分布交叉算子得到后代个体x1与x2，i表示个体染色体基因串的第i个变量，因此其交叉过程如下：

①随机地生成一个范围在(0,1]之间的数p。

②比较p与给定的交叉概率阈值Pm的大小关系，以Pm=0.5举例说明。

如果p<0.5，则：

如果p>0.5，则：

式中|N(0，1)|表示一个服从标准正态分布的随机变量。

在一维搜索空间中，分别使用传统交叉算子和正态分布交叉算子对个体进行遗传操作，在给定两个父代个体进行交叉运算1000次，分别产生2000个后代个体，并比较后代个体在搜索空间的分布情况，给定两个双亲个体进行交叉运算1000次，父代个体p1与p2初值分别设为0.7、0.2，结果如图6、图7所示。

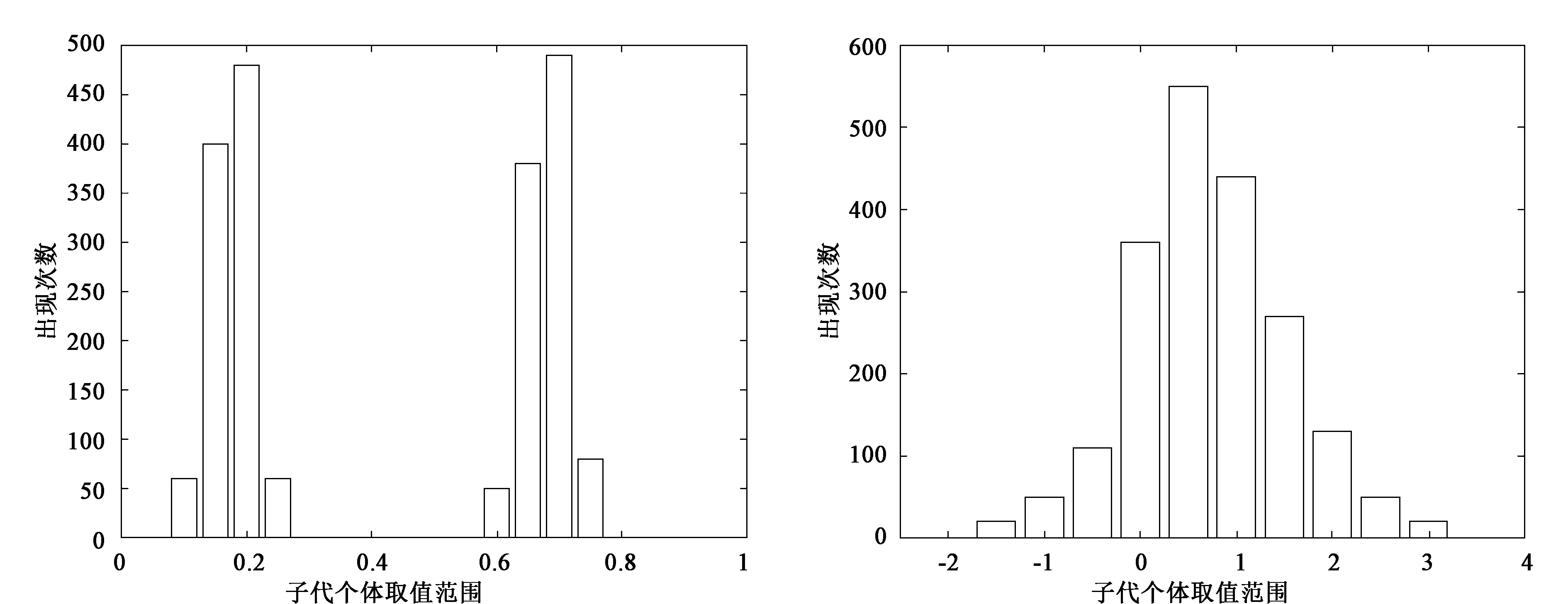
图6 传统交叉算子搜索空间分布情况 图7 正态分布交叉算子搜索空间分布情况

经过正态分布交叉算子得到的新个体取值范围为(-1.5，3.5),而通过模拟二进制交叉算子得到的新个体取值范围在(0.1，0.8)，显然正态分布交叉算子得到的新个体在搜索空间分布更加均匀且搜索空间更加广泛。

(2)自适应调整变异算子

传统的NSGA-Ⅱ算法的变异操作大多采用多项式变异方式，使用这种变异算子主观性较大，且收敛性能不佳，通过对编译方式的调整，可以提高种群进化过程的收敛速度，增强种群多样性。自适应调整变异算子操作过程如下：

将个体变异概率Pm(xi)表示为

改进的NSGA-II算法的基本过程可归纳如下：

(1)随机产生种群规模大小为M的初始父代种群Pt，采用实数编码方式对种群个体基因编码，并进行解码操作，计算个体在各目标函数上的值；

(2)基于种群个体在各目标函数上的值，对父代种群Pt进行快速非支配排序，将个体所在前沿面分配rank值，并计算个体拥挤度；

(3)按锦标赛机制从父代种群Pt中选择M/2的个体组成配对种群，并对其进行正态分布交叉算子、自适应调整变异算子操作生成大小为N的子代种群Qt，将父代种群Pt与子代种群Qt合并为大小为2M的种群；

(4)对合并后的种群进行非支配排序，以种群各个体前沿面rank值和拥挤度为依据，选择M个个体形成种群取代父代种群Pt；

(5)重复上述步骤直至满足终止条件。

3.2 NSGA-II算法寻优结果

从图8中选择3组改进NSGA-II寻优的优化参数(I,f)进行解码，计算其在各目标函数的值，并且与该优化参数在有限元模型计算获得的仿真值进行比较。通过表3可知，该模型获得的优化参数在各目标函数上的模型值与有限元模型的仿真值误差不大，在F1、F2目标函数上，模型值与仿真值的最大相对误差分别为3.1%、15.8%，进一步表明该方法在电磁式卷烟加热器多目标优化问题的有效性。

图8 改进的NSGA-II寻优的Pareto解集

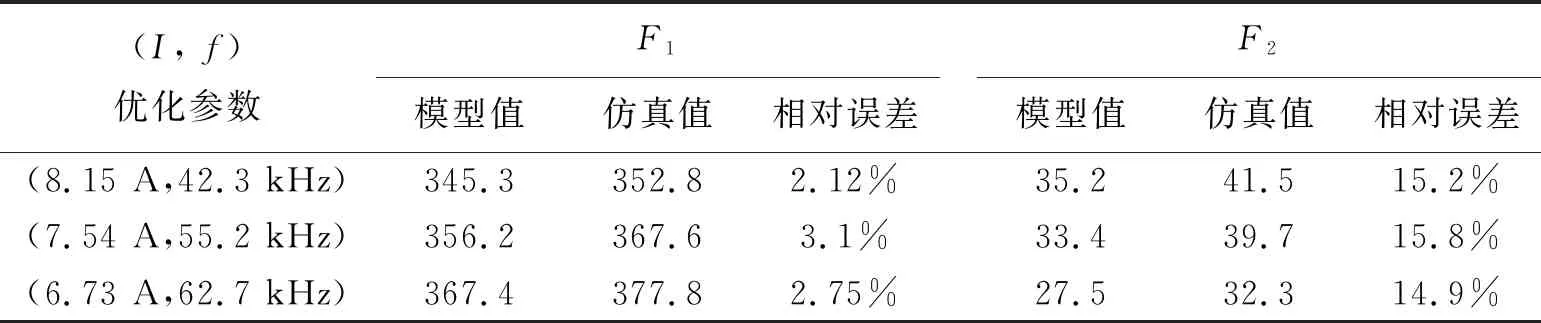
(I, f)优化参数F1模型值仿真值相对误差F2模型值仿真值相对误差(8.15 A,42.3 kHz)345.3352.82.12%35.241.515.2%(7.54 A,55.2 kHz)356.2367.63.1%33.439.715.8%(6.73 A,62.7 kHz)367.4377.82.75%27.532.314.9%

4 结论

本文采用了一种基于支持向量机和改进的快速非支配排序遗传算法相结合的多目标遗传算法对电磁式卷烟加热器感应加热参数进行全局优化，利用有限元软件Comsol对烟具仿真模型计算获得训练样本，建立了烟具发热元件的输出温度与上升时间SVM回归模型，并利用遗传算法对核参数与惩罚因子进行优化，将所获得的回归预测模型输出作为改进的NSGA-II算法的待优化目标函数进行计算得到Pareto解集。通过该方法获得的优化参数经有限元模型验证，两者误差较小，表明了该方法的有效性；与其他算法相比，该方法可实现对多个目标函数的优化，其优化过程是对整个搜索空间的解并行搜索，克服了很多传统方法可能陷入局部最优的缺陷。