基于非稳态传热理论的低密度烧蚀材料传热仿真研究
2021-10-26李添骄骆洪志李倩云李泽琛吴会强
李添骄,骆洪志,李倩云,李泽琛,吴会强
(北京宇航系统工程研究所,北京,100076)
0 引 言
低密度烧蚀材料在航天器舱体外表面和火箭壳体外表面的防热方面具有广泛的应用[1~4], 适用于高焓、低热流、再入加热时间较长的弹道式或半弹道式再入热环境,可用于飞船和返回式卫星的防热结构。按烧蚀激励的不同,烧蚀材料可分为碳化型、熔化型和升华型等类型。这种材料在飞行器外侧表面连续的高温热流作用下,热流及热量不能迅速地从表面传到内部,表面材料会发生诸如分解、熔化、蒸发、升华、侵蚀等物理以及化学变化,并且随着这些材料表面变化带来的质量消耗,吸收大量的热,同时产生高黏度的熔融液态层,阻塞热流,从而将飞行器外部热流阻断,令飞行器内部维持一定的温度,已达到保护的目的。其中低密度烧蚀材料具有密度低、烧蚀隔热性能好等特点,备受关注。
由于低密度烧蚀材料受热后首先发生材料热解、挥发等过程,材料的热性能参数(导热系数、导温系数)随时间发生变化,通过传热学理论建立热性能参数随时间变化规律非常困难,无法准确获得,因此目前阶段,针对低密度烧蚀材料的研究很多[5~11],但基本都是通过实际试验(采用电弧风洞或静态石英灯)的方式,对试验件进行防热性能的考核,这种方式需要新投产试验件及试验设备,价格昂贵且时间周期长。
本文建立了低密度烧蚀材料的一维非稳态传热模型,并将文献[12]中的试验参数带入本模型,通过仿真和试验结果的比较,验证了本模型的有效性,为今后的低密度烧蚀材料传热特性研究提供了一种有效的仿真工具。
1 模型建立
1.1 问题抽象
通过分析,本文将文献[12]中的静态隔热试验抽象为如下传热问题:
一个厚度为17 mm的无限大平壁(即低密度烧蚀材料,壁厚为17 mm),两面均为对流换热边界条件,初始时,两侧流体温度与壁内温度一致,tf1=tf2=20℃;已知两面对流换热系数分别为
由于低密度烧蚀材料受热后首先发生材料热解、挥发等过程,材料的热性能参数(导热系数、导温系数)随时间发生变化,通过传热学理论建立热性能参数随时间变化规律非常困难,因此其他工作者大多未对低密度烧蚀材料的烧蚀传热仿真进行过研究。本文针对文献[12]中编号为LDC-2A的低密度烧蚀材料,根据试验数据对其热性能参数进行曲线拟合,得到壁的导热系数满足方程:
导温系数满足方程:
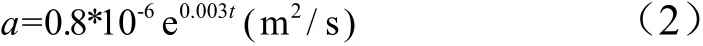
式中t为温度。
如果在正面用石英灯管进行加热,总加热量为21 000 kJ/m2,总加热时间为720 s,计算背面温度随时间变化情况如图1所示。

图1 石英灯加热试验示意Fig.1 Structure Diagram of Quartz Lamp to Heat the LDTPCM
1.2 问题分析
此问题属于以第1类边界条件下常物性、无内热源大平壁的一维非稳态导热问题,满足微分方程:

建立物理模型,如图2所示。
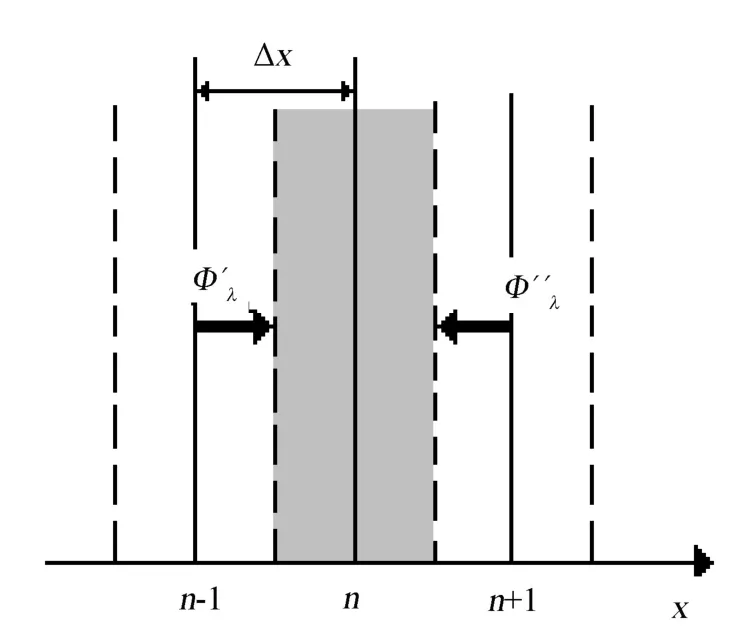
图2 简化模型示意Fig.2 Structure Diagram of Simplified Model
1.3 数值求解分析
1.3.1 求解域的离散
设空间步长为Δx,时间步长为Δτ,Δx、Δτ大小的选择需要满足节点温度方程求解的稳定性要求。为空间节点n在iΔτ时刻(简称为i时刻)的节点温度,如图3所示。

图3 空间节点Fig.3 Structure Diagram of Space Joint
1.3.2建立节点温度差分方程
通过热平衡法,建立非稳态导热物体内部节点和边界节点温度差分方程。
a)正面起始节点的温度差分方程。

式中qw为热流密度。
b)内部节点温度差分方程。
如果采用向前差分的方法列出节点n的温度对时间的变化率,热平衡方程式可写为

可得内部节点温度方程的显式差分格式:
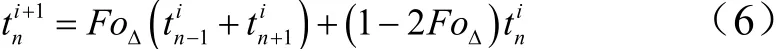
其中:

式中FoΔ是网格傅里叶数,同时由式(5)可知,差分计算中,必须满足显式差分格式的稳定性条件,即:

c)背面节点温度差分方程。


通过初始条件,并根据式(1)、式(2)、式(4)、式(6)、式(9),即可迭代计算出各节点温度变化。迭代中,需注意满足式(8)和式(10),如果出现不满足的迭代过程出现,应调整Δx、Δτ大小(一般为减小Δτ或增大Δx),并重新进行迭代仿真。否则可能会出现解不收敛或者温度出现负值等错误情况。
2 试验结果与讨论
低密度烧蚀材料背面温度随时间变化情况的Matlab数值仿真结果和文献[12]中的试验结果如图4所示。
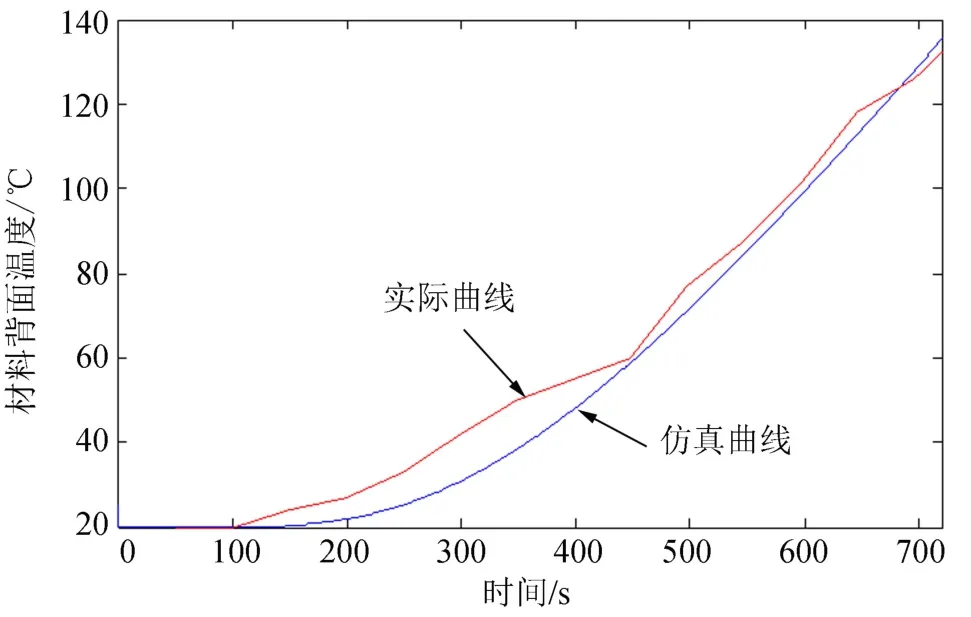
图4 材料背面温度随时间变化情况Fig.4 LDTPCM’s Back Temperature Change with Time
从图4中可以看出,前100 s内,材料的初始温度基本维持在20 ℃不变,本阶段是低密度烧蚀材料的吸热过程,从100 s开始,材料温度开始逐渐升高,至720 s仿真结束时,仿真温度达到130 ℃左右,本阶段是低密度烧蚀材料的热解、挥发、隔热过程,随着时间的增长,烧蚀材料的碳化层逐渐加厚,导热系数和导温系数逐渐加大,故材料的背温上升速度逐渐加快。本文提出的低密度烧蚀材料传热模型可以较好的吻合实际试验中的趋势,证明了本文模型的正确性和有效性。
图5展示了仿真结束(720 s)时材料中各节点的温度分布情况。
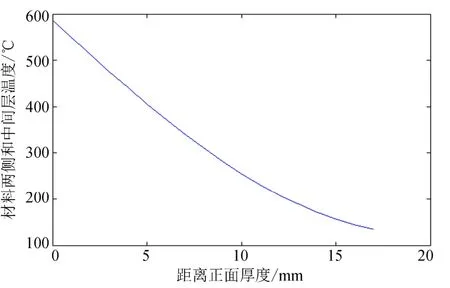
图5 材料中各节点在720s时的温度分布情况Fig.5 Temperature of LDTPCM’s Space Joint
从图5中可以看出,距离材料正面越远,节点的温度越低,材料正面温度达到590 ℃左右,通过低密度烧蚀材料的有效隔热,材料背面温度降低到130 ℃左右,低密度烧蚀材料对热流进行了有效的阻隔。
3 结 论
本文对静态石英灯加热低密度烧蚀材料的传热学进行抽象。低密度烧蚀材料受热后首先发生材料热解、挥发等过程,材料的热性能参数(导热系数、导温系数)随时间发生变化,通过传热学理论建立热性能参数随时间变化规律非常困难。本文首先对低密度烧蚀材料的热性能参数试验进行筛选和曲线拟合,找出低密度烧蚀材料的热性能参数(导热系数、导温系数)随时间的变化关系,之后建立了低密度烧蚀材料的一维非稳态传热学模型,通过仿真结果及与文献[12]中的试验数据进行对比,证明了本文模型的正确性和有效性。
采用仿真分析的手段,对低密度烧蚀材料在烧蚀过程中的热性能参数进行拟合,得到热性能参数的函数表达式,可以针对此类低密度烧蚀材料进行不同厚度、不同初始热流条件下的仿真分析,有效地缩短了航天防热材料在方案论证初期,大量筛选试验的时间周期,并减少方案论证初期的资金投入,为今后低密度烧蚀材料在航天中的传热学仿真提供了一种有效的仿真工具。
