运载火箭金属膜盒式蓄压器振动及疲劳特性研究分析

2021-10-26王丛飞郑茂琦

导弹与航天运载技术 2021年5期

王丛飞，许光，张婷，郑茂琦，满满

（北京宇航系统工程研究所，北京，100076）

0 引言

POGO振动是大型液体火箭推进剂系统液路的振动与结构纵向振动相互耦合作用的一种不稳定的闭环自激振动。POGO振动会使火箭低频振动环境恶化，箭上仪器可靠性较低，使宇航员生理系统失调[1～3]。为了抑制火箭发生POGO振动，中国现役火箭主要采用金属膜盒式蓄压器进行减振设计。蓄压器安装在氧路输送管进入涡轮泵的上游，振动环境较为复杂，同时，膜盒受到液路压力的反复挤压，因此，对蓄压器的疲劳寿命造成了很大的挑战。

蓄压器方案设计阶段，主要考虑蓄压器的结构振动特性，未对实际工作状态下的振动特性进行设计。实际上，膜盒在充压后的振动特性与未充压的状态有显著差异，膜盒的结构固有频率并不能代表其真实充压状态的特性。但由于蓄压器实际工作下存在气、液、固的三相耦合，振动特性计算较为复杂，并没有较为准确的理论分析方法；此外，低温火箭蓄压器工作环境更为复杂，由于缺少有效的分析方法，主要采用典型特性试验验证，直接导致产品成本高、周期长，对运载火箭的高密度发射产生较为严重的影响。

本文采用Abaqus对蓄压器在充压状态下的振动特性进行了研究分析，并采用n-code疲劳分析软件对特定振动条件下蓄压器的疲劳寿命进行计算。通过以上研究，确定了蓄压器有限元仿真分析的方法，同时，根据分析结果，给出了液路压力对蓄压器振动特性的影响规律。

1 蓄压器基本介绍

金属膜盒式蓄压器的结构见图1所示，主要结构包括壳体与膜盒组件。壳体的主要功能为连接输送管及膜盒，膜盒为蓄压器的主要弹性元件，膜盒的结构如图2所示。

图1 金属膜盒式蓄压器示意Fig.1 Schematic Diagram of Metal Bellows Accumulator

图2 膜盒的结构示意Fig.2 Schematic Diagram of Bellows Structure

金属膜盒式蓄压器在射前根据能量值（PV）要求，向膜盒内充一定压力（P0）、一定体积（V）的气体，使膜盒具备一定的充压刚度，用于缓冲由于液路压力波动造成的振动，起到缓冲降频的作用[4]。

液路压力加载后，随着膜盒受到挤压，膜盒内压力会随之升高，同时，膜盒体积降低，但总能量值（PV）保持不变。由于膜盒的机械刚度相比气体刚度可忽略不计，因此，膜盒升高后的压力基本与输送管液路压力一致。

2 振动特性分析

2.1 有限元模型

蓄压器膜盒在实际工作中，不同膜盒之间的相互挤压可能发生耦合效应，为了真实模拟蓄压器的振动特性，一般蓄压器振动特性分析至少选取双膜盒模型。图3给出了蓄压器有限元基本模型。

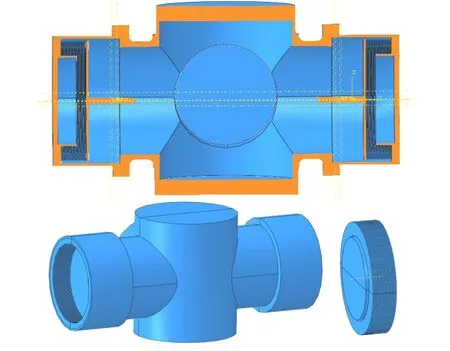
图3 蓄压器有限元模型（结构、流体域、气体域）Fig.3 Finite Element Model of Accumulator(Structure, Fluid Domain, Gas Domain)

图3中，流体介质为液氮（试验状态，工作状态为液氧），气体介质为氦气，介质的温度均为80 K。流体介质、气体介质的体积参数与实际工作压力有关，在给定（输送管）工作压力下，根据膜盒的能量值（PV恒定），计算膜盒在压缩状态下的体积，并结合膜盒的结构参数计算实际压缩量[5]，再分别得出流体介质与气体介质的实际单元参数。

2.2 材料属性

蓄压器主要采用不锈钢材料，流体介质采用液氮、气体介质选用氦气。采用有限元模拟流体、气体介质进行动力学分析，需明确体积模量、密度属性。在80 K温度，液氮的体积模量、密度随压力变化不明显。但是，氦气在不同压力下，体积模量及密度均有显著的变化，因此，针对不同压力工况下的蓄压器，需分别设置介质属性信息。表1给出了蓄压器的结构材料属性，表2给出了液氮、氦气在80 K温度下，不同压力条件下的体积模量、密度参数。

表1 不锈钢力学性能参数Tab.1 Mechanical Property Parameters of Stainless Steel

表2 流体、气体介质在不同压力下的属性Tab.2 Properties of Fluid and Gas Media under Different Pressures

2.3 边界条件

蓄压器振动分析的约束条件为下法兰进行安装固定，上法兰为自由状态，与试验状态保持一致[6]。有限元模型边界条件见图4所示。

图4 蓄压器边界条件Fig 4 Boundary Conditions of Accumulator

膜盒的实际结构简化了导向位置，采用点与面coupling的方式进行连接，同时对参考点约束除轴向以外的自由度。参考面的选取需根据液路压力确定膜盒的压缩量，计算确定导杆与导向孔的实际接触位置。

图5 导向杆边界条件Fig 5 Boundary Conditions of Guide Rod

2.4 模态分析结果

对蓄压器在0.43 MPa、0.55 MPa、0.66 MPa液路压力下膜盒的振动特性进行计算分析，得到了前5阶主要模态及对应的频率。蓄压器主要分为壳体及膜盒组件，壳体相比膜盒组件的刚度强较多，因此，对应的主要模态特性为膜盒振动的局部模态。表3给出了在不同压力边界条件下膜盒的振动频率。

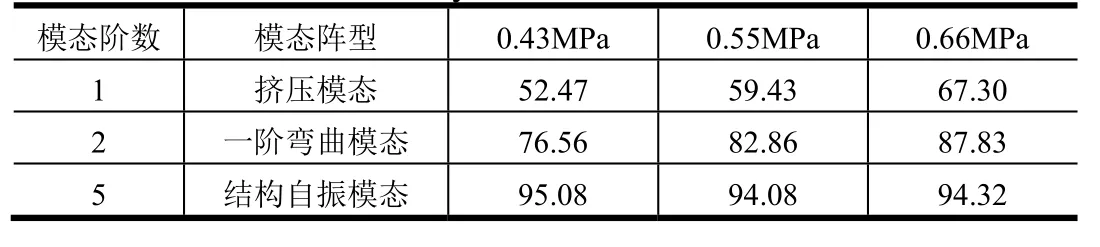
表3 蓄压器在不同压力边界条件下的振动特性Tab.3 Vibration Characteristics of Accumulator under Different Pressure Boundary Conditions

图6给出了以上模态对应的振型，依次为两膜盒通过液体介质相互挤压的模态、膜盒轴向弯曲振动的模态、膜盒结构自振的模态。其中3阶、4阶模态与2阶模态类似，属于不同方向的弯曲模态。

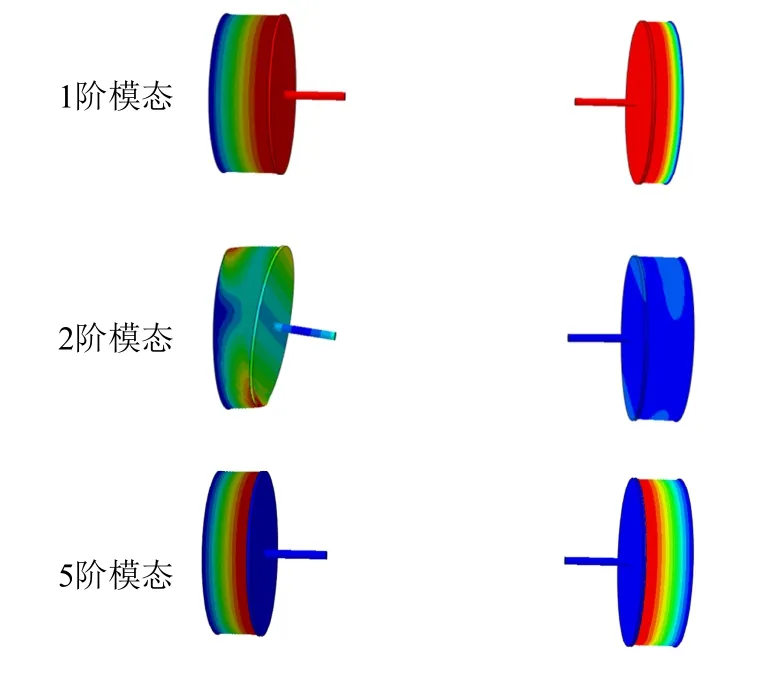
图6 蓄压器膜盒的振型Fig.6 Vibration Mode of Accumulator Bellow

从分析结果可见，随着液路压力增加，膜盒的1阶、2阶振动频率升高。在0.43 MPa压力下，膜盒的一阶弯曲模态低于80 Hz，在0.55 MPa、0.66 MPa压力下，膜盒一阶弯曲模态高于80 Hz。膜盒的第5阶振动频率为结构自振的频率，随液路压力变化不明显。

3 疲劳寿命分析

3.1 疲劳分析设置

在完成蓄压器的振动频率分析后，对蓄压器开展了模态动力学分析，将模态动力学分析结果，作为疲劳寿命分析输入。采用疲劳分析软件n-code对蓄压器进行了随机振动疲劳寿命分析。分别设置输入蓄压器模态动力学分析结果、力学环境条件、振动分析时间、材料参数等[7]。

3.2 疲劳分析结果

计算得到了蓄压器在不同压力边界条件下振动100 s的损伤值、最大均方根应力以及应力谱密度曲线。结果显示，在液路压力0.43 MPa下的损伤值、最大均方根应力相比0.55 MPa、0.66 MPa工况下明显要低（见表4），与经验认识压力越高膜盒越稳定明显不同。

表4 蓄压器膜盒在不同压力边界条件下疲劳分析结果Tab.4 Fatigue Analysis Results of Accumulator Bellow under Different Pressure Boundary Conditions

为了探究原因，对应力谱密度曲线进行了研究分析，图7给出了在压力0.43 MPa和0.55 MPa下的应力谱密度曲线。

图7 应力谱密度曲线Fig.7 Stress Spectral Density Curve

从图7的应力谱密度曲线可看出，对于的损伤积累最大的点主要在1阶弯曲频率、膜盒的自振频率处。在压力为0.43 MPa时，1阶弯曲频率对应的模态为76.56 Hz，低于80 Hz，对应的功率谱密度较小，产生的损伤较小，主要损伤积累在膜盒自振频率95.08 Hz，对应的最大应力谱密度为7502 MPa2/Hz。随着膜盒压力升高，在0.55 MPa外压下，膜盒的1阶弯曲频率提高到82.86 Hz，因此该模态对应的损伤显著增大，对应的最大应力谱密度为28 400 MPa2/Hz；自振频率处对应的最大应力谱密度变化不明显，仍在8000 MPa2/Hz左右，可见1阶弯曲模态对膜盒的疲劳特性有重要影响。

蓄压器膜盒为压力敏感元件，在承受轴向拉压的过程对其产生的损伤较小，但在发生弯曲振动时，对膜盒产生的损伤较大。因此，在膜盒的1阶弯曲频率处，如果振动激励较为严酷，将对膜盒造成较大的损伤，因此，在设计过程中应将一阶弯曲振动频率避开高能量频段，同时，可从结构角度，对膜盒的轴向导向结构进行加强，使结构由于弯曲振动造成的疲劳损伤降低。