弹性大惯量电动舵系统颤振抑制*
2021-10-26苏伟杰王厚浩罗明亮徐志伟
苏伟杰,陈 辉,王厚浩,罗明亮,何 洋,徐志伟
(上海航天控制技术研究所·上海·201109)
0 引 言
当前,无人机技术飞速发展。无人机舵机作为无人机系统的重要组成部分,主要用来控制左右副翼、方向舵、升降舵和油门的定位,从而维持飞行姿态的稳定。国内外针对无人机舵机系统也做了大量的研究。Volz公司、Futaba 公司、Parker 宇航、霍尼韦尔、Micropilot等国际知名企业均在无人机电动舵机领域积累了丰富的经验,形成了系列化小功率电动舵机的研制生产能力。此外,美国空军、海军和NASA研制的电动舵机在F/A-18B 系列飞机上进行了测试。国内,北京航空航天大学、西北工业大学、哈尔滨工业大学、上海航天控制技术研究所等单位也开展了针对无人机用电动舵机的研究,但在产品化方面仍与国外存在一定的差距。
某型国产化大型商业无人机由现有成熟飞机运5改制,是国内首款在有人货运飞机上进行改制的无人机。由于未改变原飞机的整体机械结构布局,该无人机升降舵以及方向舵舵面惯量较大,同时舵机与舵面间为连杆机构和钢丝绳结构。升降舵与方向舵为典型的大惯量、低刚度电动舵机系统。实际系统中的传动系统由多级连杆组合而成,间隙、弹性特性和大惯量的存在,必然会导致一定程度的机械颤振。机械颤振会在特定情况下激发整个系统产生周期性振动。
针对电动舵机系统的机械颤振问题,大量的文献给出了理论分析与研究,从传动刚度、间隙、惯量、阻尼等角度给出了相应的解释。文献[2]建立了舵机-舵面耦合系统的数学模型和颤振特性分析方法,提出在舵机电流环加入对超前滞后环节进行颤振抑制的措施。文献[3]对舵机系统的动刚度进行了研究分析,通过分析舵机系统的动刚度特性,得出了一些具有工程意义的结论。文献[4]对飞机的非线性气动弹性产生因素进行了分析,并得出了颤振产生的主要原因。文献[5]利用气动和结构学科各自的工程方法对大型民用飞机的概念方案进行了气动弹性建模与计算,并以大型民用飞机为算例进行了分析研究。本文对弹性大惯量电动舵系统颤振的原因进行了分析,通过数学建模与仿真分析,验证了双惯量系统产生颤振的原因。针对无人机系统在试验中出现的舵面末端颤振现象,在现有方案的基础上提出了改进措施,以适应工作环境的不确定性,并通过飞行试验验证,检验了措施的有效性。
1 数学建模
在负载大惯量的机电舵系统中,系统的内在控制特性,特别是稳态附近的小信号特性,是需要重点关注的。因此,不能将电机与负载看成一体,将其简化为一个简单的刚体运动而进行建模。对于实际系统,即便电机与负载是直接耦合的,但传动本质上是弹性的。在电机驱动力矩的作用下,传动机构会产生某种程度的弹性变形。对加速度要求大、对快速性和精度要求高的系统,或对转动惯量需求大、对性能要求高的系统,其弹性变形不能忽略。
该型无人机方向舵与升降舵由电机轴驱动多级弹性关节与刚性负载实现连接,是一种典型的双惯量系统。在双惯量系统中,舵机输出侧和舵面负载侧均为刚性且具有转动惯量,中间为弹性传动机构,如图1所示。

图1 无人机双惯量舵系统传动示意图Fig.1 Schematic diagram of UAV dual inertia rudder system transmission
系统控制框图如图2所示。

图2 系统控制框图Fig.2 System control block diagram
该舵系统的双惯量数学模型可表示为

(1)
其中,T
、T
分别为舵机输出转矩、舵面负载转矩;J
、J
分别为舵机输出侧惯量、舵面负载侧惯量;θ
、θ
分别为舵机输出侧位置、舵面负载侧位置;C
、C
分别为舵机输出侧阻尼、舵面负载侧阻尼;K
为传动刚度。由于该系统阻尼均比较小,可认为C
≈C
≈0。将式(1)进行拉普拉斯变换后,求解方程组,可得舵面端传递函数为
(2)
由式(2)可知,该系统传递函数由一个二阶纯惯性环节和一个二阶振荡环节组成,舵面的谐振频率为
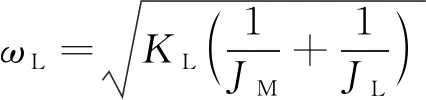
(3)
由此可见,双惯量系统的舵面颤振主要与系统的惯量和传动刚度有关,刚度越大、惯量越小,系统的谐振频率越高,舵面颤振的概率就越小。电动舵机传动机构均会存在一定的间隙和弹性。根据研制经验,传动机构刚度不足、间隙控制不严及负载惯量过大,均易导致舵系统发生颤振。
2 舵机方案设计
根据能源体制要求,无人机舵机的驱动电源为28V,控制电源经电源变换形成二次电源,供舵机控制电路使用;舵机采用了位置反馈随动电动伺服方案,控制器采用了控制电路板加驱动器模块的方案。舵系统在供电后,接收舵偏指令进入控制器,与AD采集的舵反馈信息共同进入DSP,在完成信号处理和控制算法解算后,形成驱动电机所需的PWM调制信号。最后,由功率驱动器产生推动电机转动的电流,电机转矩和转速通过减速传动机构被传递到舵面,操纵舵面偏转。
舵机采用“电机+齿轮副+直齿滚珠丝杠+拨叉+角位置反馈电位计”的方案,电机转动经传动机构(齿轮+滚珠丝杠)带动拨叉驱动舵轴偏转,进而带动摇臂偏转,反馈装置采用角位移电位计。控制器主要由控制板与电机驱动器组成。舵机总体结构布置如图3所示。

图3 结构布局图Fig.3 Structural layout
控制器是构成舵机伺服闭环系统的关键部件,其主要任务是接受弹载计算机给定的位置指令和反馈电位计给出的舵偏角信号。将信号送至数字信号处理器进行处理,形成驱动电机所需的调制信号,再经由功率驱动器产生推动电机所需的电流。在舵机中,控制器以数字处理器为控制核心,主要由电源变换电路、信号适配电路、A/D采集电路、DSP处理电路、电机驱动电路模块和接口电路组成。其原理框图如图4所示。

图4 数控驱动组合原理框图Fig.4 Principle block diagram of NC drive combination
在电路中,反馈电位计经运放电路预处理,被输入至AD处理芯片进行转换。AD处理芯片同时将功率母线电流信号和电源电压监控信号进行转换,并将其一并输入至DSP芯片。DSP通过422接口电路接收上位机舵指令信号,将信号与反馈信号进行解算。DSP解算完毕后,信号将形成控制电机所需要的PWM信号及电机换向信号,并被输入至电机驱动模块,驱动电机按要求旋转。
舵机控制软件运行在控制器的DSP中,负责接收舵指令信号,采集舵反馈信号,采集电流模拟信号,并根据这些信息完成控制算法解算,输出相应占空比的PWM信号,驱动功率电路,以实现对执行机构的控制。舵系统的软件流程如图5所示。
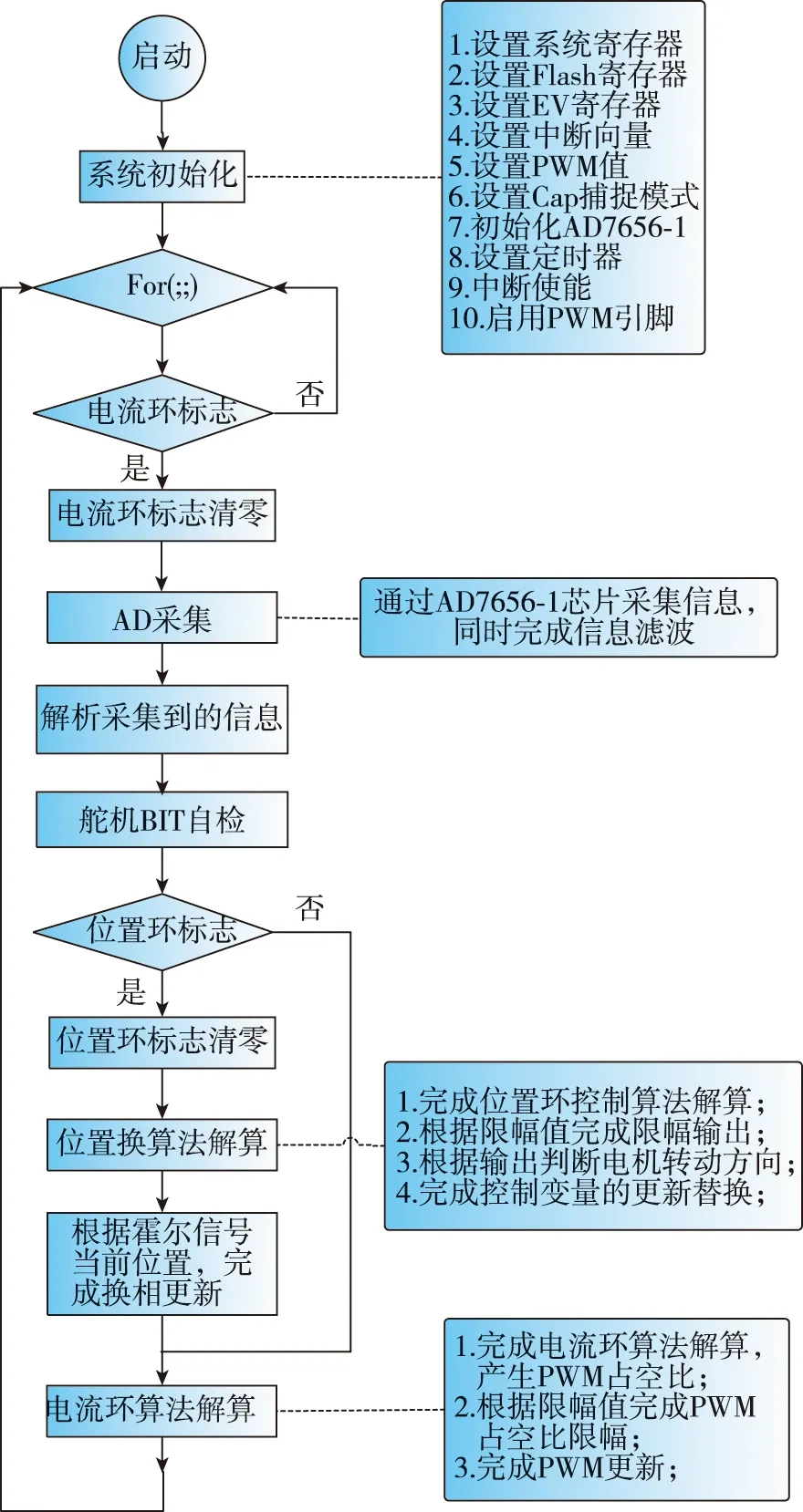
图5 软件流程图Fig.5 Software flow chart
3 双惯量舵系统的仿真分析
舵机舵轴到舵面之间,存在多级弹性连接机构,系统的传动刚度、间隙、惯量、阻尼将对舵机性能产生重要影响。结合系统数学模型,验证上述因素对舵系统的影响,利用Matlab进行仿真分析。为了验证不同因素对舵系统的影响,设计了如下四组对比试验。仿真结果如图6~图10所示。
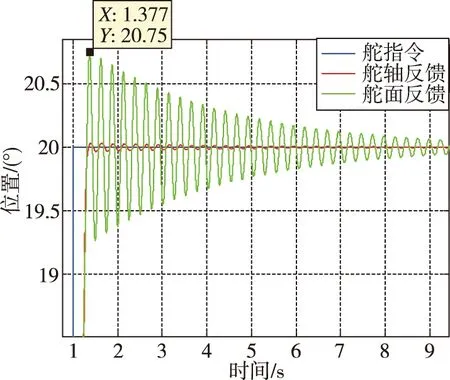
图6 KL=50响应曲线 Fig.6 Response curve of KL=50

图7 KL=500响应曲线Fig.7 Response curve of KL=500
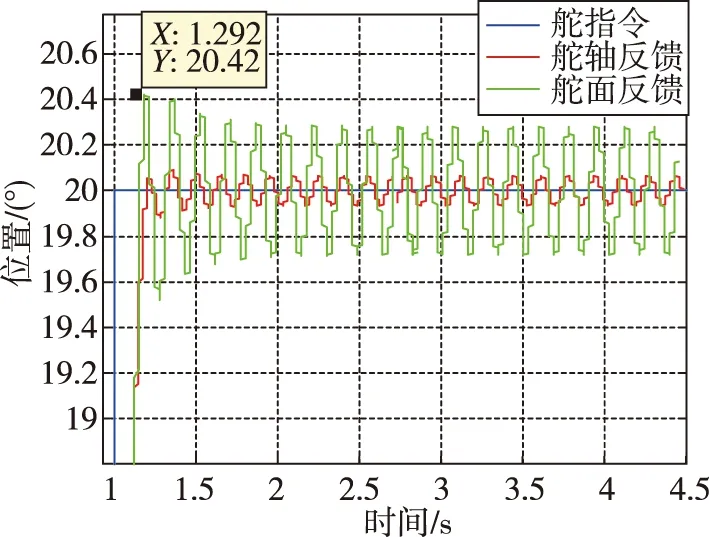
图8 增加间隙响应曲线Fig.8 Response curve of clearance increased

图9 增加惯量响应曲线Fig.9 Response curve of inertia increased

图10 增加阻尼响应曲线Fig.10 Response curve of damping increased
(1)设定舵系统相关参数不变,改变舵机输出轴至舵面的传动刚度。设定舵面惯量J
=4.5kg·m,分别设定传动刚度系数K
=50、K
=500,以进行仿真;(2)设定舵系统相关参数不变,改变舵机输出轴至舵面的传动刚度。设定舵面惯量J
=4.5kg·m,设定刚度系数K
=500,设定舵轴输出到舵面间隙为0.1°;(3)设定舵系统相关参数不变,改变舵机输出轴至舵面的传动刚度,改变舵面惯量为J
=18kg·m,设定刚度系数K
=500;(4)设定舵系统相关参数不变,设定舵面惯量为J
=18kg·m,设定刚度系数K
=500,增加舵机阻尼。由图6、图7的对比可知,在提升系统传动刚度后,舵面的颤振频率提高,舵面颤振的幅值与时间明显降低;由图7、图8的对比可知,系统传动间隙增加后,系统出现持续颤振,传动间隙的存在易于激发舵面的颤振;由图8、图9的对比可知,负载惯量增加后,舵面颤振幅值有所增加;由图9、图10的对比可知,增加系统阻尼可以显著抑制舵面颤振。由此可见,双惯量系统的颤振抑制与系统的传动刚度、传动间隙、负载惯量、系统阻尼均有一定关系。
4 颤振抑制的改进措施
颤振的抑制方法主要有两种,一种是通过改进工艺方法,调整机械传动机构的结构特性,将自然振动频率提升到系统带宽之外,来消除舵面颤振;另一种方法是通过设计控制算法,调整系统控制性能,在不改变传动系统的前提下抑制舵面残留颤振。
4.1 改善机械传动机构
在机械传动方面,通过改变无人机舵系统的传动刚度、传动间隙、负载惯量、系统阻尼,均可改善系统的颤振。但由于生产工艺的局限和实际的需求,系统传动刚度与舵面负载惯量的改善空间有限,在尽可能避开系统谐振频率的基础上,可以从控制电动舵机的传动间隙与系统阻尼入手,以改善系统的颤振现象。通过调整电动舵机的调隙垫片,控制合理的预紧力,来改变系统的间隙与阻尼,调隙垫片的安装示意图如图11所示。通过无人机实际舵系统测试,将预紧力调整为0.4N·m,试验结果对比如图12、图13所示。在相同指令下,舵面的残留颤振时间由改进前的2.1s减少为1.2s。

图11 调隙垫片安装示意图Fig.11 Schematic diagram of adjusting gap

图12 改进前响应曲线 Fig.12 Response curve before improvement

图13 改进后响应曲线Fig.13 Response curve after improvement
4.2 改进颤振抑制控制算法
目前,输入整形器是伺服系统颤振抑制中常用的一种方法,其具有结构简单、无需改变系统原有结构、不影响原有系统稳定性等优点。输入整形器是一种基于指令信号的前馈控制方法,其基本原理为将易于激发系统颤振的指令信号与脉冲序列进行整形处理,使由不同信号带来的颤振相互抵消,从而达到抑制舵面颤振的效果。输入整形器主要可分为零振动输入整形器(Zero Vibration,ZV)、导数零振动输入整形器(Derivative Zero Vibration,ZVD)和极不灵敏输入整形器(Extremely Insensitivity,EI)三种,三种控制器均能消除舵面的颤振。其中,ZV输入整形器的动跟踪性能最好,ZVD控制器与EI控制器的鲁棒性更强。由于位置控制是被周期性执行的,输入整形器应在每个控制周期内对输入位置指令进行整形。实际系统为离散系统,由输入产生的响应时滞会延后n
拍。整形器总时滞与位置环周期的比值越大,n
就越大,系统占用内存也就越大。由于系统资源有限,在系统负载阻尼振荡周期较大的情况下,ZV输入整形器可最大限度地节约系统资源。同时,该系统的颤振频率相对固定,采用ZV输入整形器可使舵系统的动态误差最小。将舵系统等效为二阶双惯量系统,系统传递函数如式(4)所示
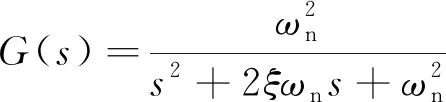
(4)
式中,ω
为系统自然振动频率,ξ
为系统阻尼系数。根据文献[14],将输入指令信号与i
个脉冲系列进行整形处理,即将i
个幅值为A
、响应时间为t
的脉冲响应序列与输入指令信号进行卷积,得到复频域表达式(如式(5)所示)。舵系统对于单位脉冲的响应函数如式(6)所示,对于n
个脉冲系统的响应y
(t
)如式(7)所示
(5)
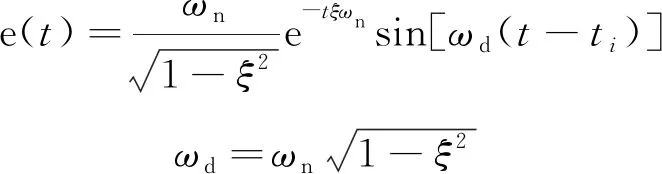
(6)
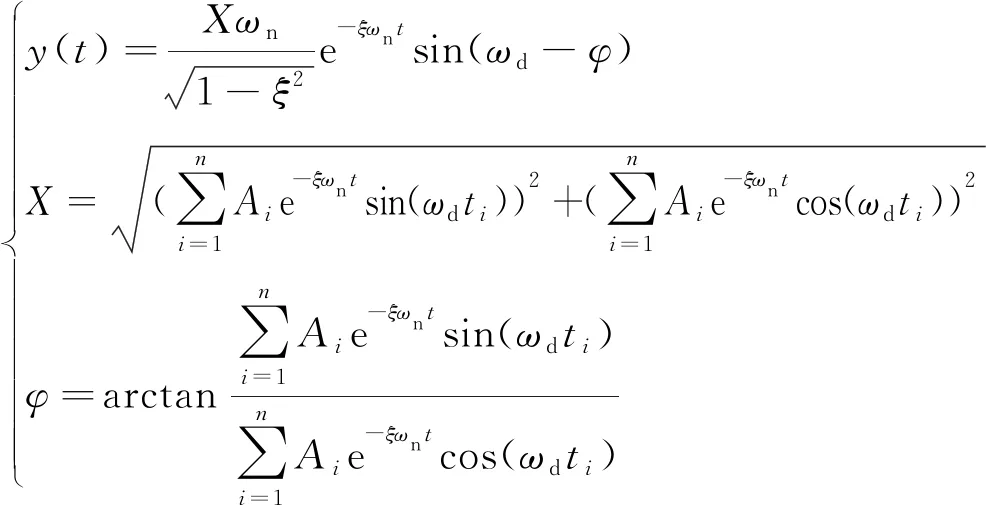
(7)
式中,A
为第i
个脉信号的幅值,t
为第i
个脉信号的作用时刻,ω
为固有阻尼频率。ZV输入整形器可表述为两个脉冲信号的叠加作用,本质上可等效为配置一个零点,与系统极点对消抑制系统颤振。根据ZV输入整形器的工作原理,脉冲信号对于整个舵系统的颤振效应主要来源于振荡环节。为了抑制这种振荡,式(7)中的振荡环节X应尽可能接近于零,可得到ZV输入整形器的表达式如式(8)所示
F
(s
)=A
e-+A
e-(8)

目前,无人机电动舵机采用的是分段位置PI伺服控制。将上述ZV输入整形器增加在位置环外,在保证输入指令响应幅值不变的情况下,可抑制舵面的颤振现象,控制框图如图14所示。
图14中,K
为电流系数,K
为力矩系数,J
为电机转动惯量,R
为电机定子电阻,L
为电机相电感,N
为电机极对数。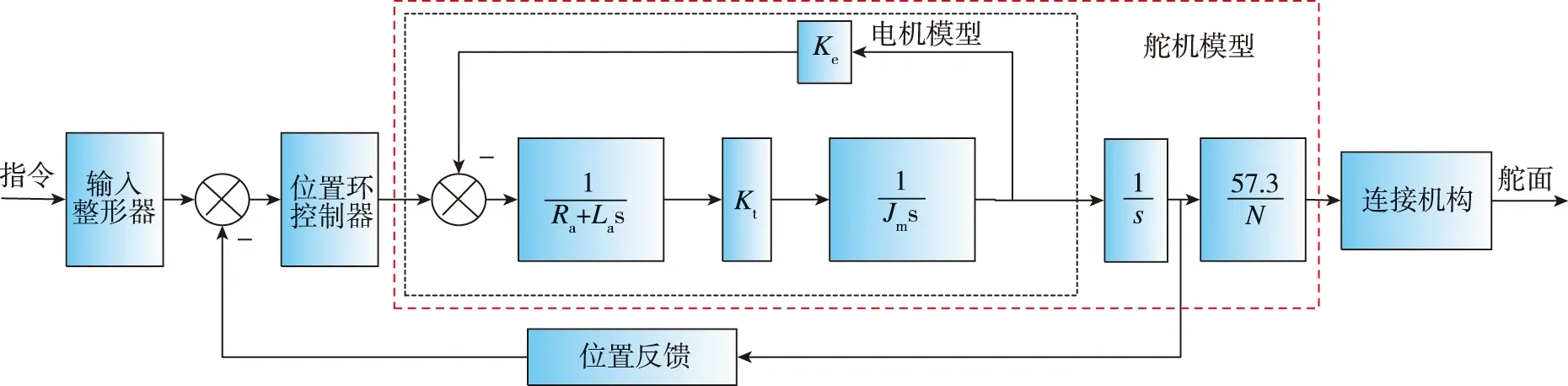
图14 舵系统控制框图Fig.14 Actuator system control block diagram
由于无法精确获得无人机的实际模态参数,根据试验结果进行估算,对是否采用了ZV输入整形器的控制结果在DSPACE平台上进行了仿真。位置环PI控制参数采取了适应性的分段设计,采用斜坡函数光滑处理各段间的切换,使其兼顾大偏差与小偏差控制的快速性与稳定性。系统仿真参数如表1所示,控制参数如表2所示,仿真对比结果如图15所示。

表1 系统仿真参数Tab.1 System simulation parameters

表2 系统PI控制参数Tab.2 System PI control parameters
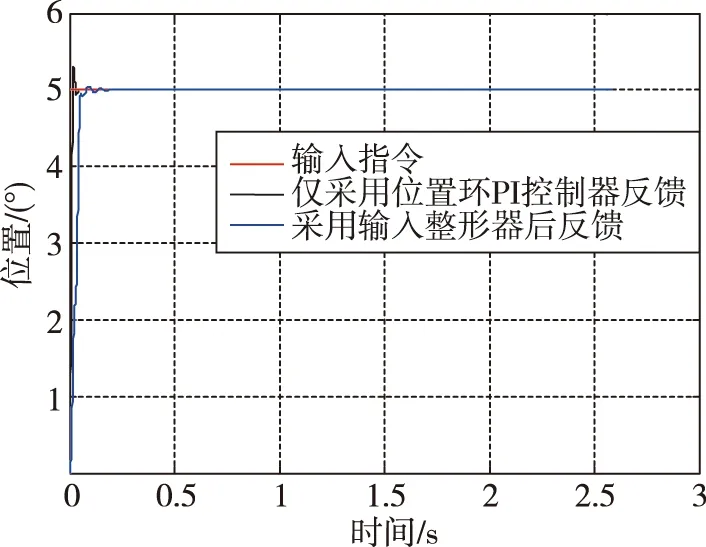
图15 半实物仿真对比曲线Fig.15 Semi-physical simulation contrast curve
由仿真结果可知,ZV输入整形器的引入很好地抑制了系统的残留抖振。为了进一步验证,在无人机实际系统中引入了输入整形器。通过调整合适的参数,基本消除了舵面的残留抖动,试验结果如图16所示。从试验结果对比可以发现,加入输入整形器后,舵面残留颤振基本被消除,颤振抑制效果比较明显。

图16 采用输入整形器的响应曲线Fig.16 Response curve with input shaper
5 结 论
本文从实际工程问题出发,介绍了无人机舵机的总体方案设计,针对某型无人机舵机舵面在特定方波指令下的颤振现象,建立了舵机-负载双惯量模型。通过仿真,对颤振现象产生的机理进行了分析,验证了传动刚度、间隙、惯量、阻尼对舵面颤振的影响。通过针对性地改善舵机传动机构和设计改进控制算法,进行了地面半实物仿真验证,并在现有无人机上加入ZV输入整形器进行了试验验证。飞行试验结果表明,通过改进措施,在未改变现有舵机总体设计方案的前提下,基本消除了舵面在方波指令下的颤振问题,保障了该大中型货运无人机的首飞。
