Stacked-GRU网络在动力随动陀螺零部件选配上的应用*

钟百鸿，王 琳，钟诗胜,，徐 松，张勇飞，刘兴兴，王杜林

(1.哈尔滨工业大学 机电工程学院· 哈尔滨·150006；2.哈尔滨工业大学(威海)海洋工程学院· 威海·264209；3.上海航天控制技术研究所·上海·201109)

0 引 言

作为红外导引头位标器的核心部件，动力随动陀螺能够消除导弹运动对测量系统的影响，对目标进行追踪，被广泛应用于空空导弹、地空导弹等制导武器中。动力随动陀螺使得制导武器具备对目标追踪的打击能力，在现代制导武器中起着举足轻重的作用。

装配是产品生产的关键环节，装配质量直接决定着产品的使用性能。在动力随动陀螺装配过程中，零部件选配组合对陀螺性能的影响很大，如陀螺的漂移性能。陀螺零部件的选配，可改善陀螺漂移性能，进而提高制导武器的精确打击能力。然而，由于陀螺的结构复杂、对装配质量的要求高，往往需要人工选配零部件并进行反复装拆调整，才能使陀螺性能满足要求。陀螺人工选配方式会产生大量的无效装配，使其难以满足当前对快速批量化生产的需求。因此，需要建立陀螺零部件选配模型。在装配开始前，以陀螺某一零部件的装配参数特征作为陀螺选配模型的输入。对待选配的零部件装配参数特征进行预测，根据预测结果匹配适合的零部件并进行选配，进而可减少无效装配，提高陀螺零部件的装配效率，以及装配质量的一致性。因此，建立陀螺零部件选配模型对于陀螺零部件装配而言具有极其重要的指导意义。

目前，针对复杂精密产品零部件的装配问题，学者在工程应用中提出了一些选配方法。刘明周等为实现多种装配要求下的曲柄连杆机构选配，提出了一种基于遗传算法和模拟退火算法的混合算法，建立了曲柄连杆机构的复合目标选配方法。宿彪等以装配尺寸链为约束条件，提出了一种基于蚁群算法的工程机械再制造优化选配方法。曹杰等针对复杂机械产品多质量要求下的选配问题，综合考虑形位公差和尺寸公差，提出了一种基于遗传算法的选配方法。段黎明等考虑到了零件尺寸链与尺寸的关联关系，建立了一种基于密度的多目标进化算法的机械产品选配方法。姜兴宇等以封闭环尺寸链为约束条件，建立了一种基于粒子群遗传算法的再制造机床优化选配方法。然而，现有的产品选配方法多是针对配合公差、形位公差等而展开的。对于动力随动陀螺这类复杂精密的产品而言，装配零部件多、测量难度大、测量成本高，往往需要根据性能变化值进行零部件的选配调整，显然难以利用现有的选配方法指导陀螺零部件的选配。另一方面，陀螺零部件的装配参数之间存在复杂的耦合关联关系，难以使用陀螺动力学等理论推导建立陀螺零部件的选配模型。

为解决上述动力随动陀螺零部件的装配问题，提高陀螺装配的效率，本文以动力随动陀螺典型零部件的装配为例，提出了一种基于数据驱动的陀螺零部件选配方法。数据驱动模型已在故障诊断、性能预测等领域中被成功应用。YUAN等采用门控循环单元(Gated Recurrent Unit，GRU)网络数据驱动模型对序列数据进行了智能故障诊断；LI等采用CNN与GRU混合神经网络数据驱动模型对齿轮进行了故障检测；WANG等采用GRU网络对智能车间实时大数据进行了处理，获得了优异的预测性能。基于数据驱动的陀螺零部件选配方法的关键在于数据驱动模型的构建，考虑到陀螺装配参数间复杂的耦合关联关系，本文建立了Stacked-GRU网络数据驱动模型以提取更多装配参数特征，最终实现陀螺零部件的精确选配。将人工智能技术应用于复杂机械产品的选配，有利于实现产品装配的智能化。本文建立的Stacked-GRU网络数据驱动模型可用于复杂精密产品(如陀螺)的装配中，通过Stacked-GRU网络有效提取装配参数间的关联关系，实现产品零部件的选配，为复杂精密产品自动化装配提供技术支撑，这是本文所提算法在复杂机械精密产品选配上的应用创新。同时，产品选配实验结果表明，本文所提数据驱动选配方法能够实现陀螺零部件的选配，且其预测精度优于传统的神经网络。

本文各部分组织如下：在第一章，描述了动力随动陀螺的装配问题；在第二章，介绍了GRU网络的基本理论，构建了Stacked-GRU网络数据驱动选配方法；在第三章，对实验结果进行了分析与讨论；最后，在第四章，总结了本文所做的工作。

1 动力随动陀螺零部件装配问题描述

作为一类复杂的精密产品，动力随动陀螺的研发成本高、零部件装配约束关系复杂。为使其装配质量满足要求，仅提高零部件的加工精度是不经济的。选配方法可以在不增加零部件加工精度的基础上，通过选配合适的零部件进行组合装配，以提高产品的装配精度，满足装配的质量要求。

目前，由于缺乏选配模型的指导，动力随动陀螺零部件的选配仍需通过人工试凑法进行产品装配。其装配流程如图1所示，具体的实施步骤如下：

步骤1

装配人员根据装配经验，任意选择零部件，并将其与待装配零部件进行装配；

步骤2

对零部件选配组合装配质量进行检验；

步骤3

若满足装配质量要求，则流入下一装配环节，否则拆解调整，重复步骤1，直至满足装配质量要求。由于装配人员经验不一，陀螺零部件装配成功率受人为影响的程度较大，陀螺装配质量的一致性难以得到保证。往往需要经过多次装拆调整，才能选配出合适的陀螺零部件组合，以满足性能要求；同时，零部件一次装配成功率低，会产生大量无效装配,降低生产效率。为解决上述陀螺装配问题，本文提出了一种基于数据驱动的陀螺零部件选配方法，如图1所示。该方法通过建立数据驱动选配模型，挖掘了零部件装配参数之间的联系，对待选配零部件属性进行了预测，以实现零部件的选配。具体而言，假设A(部件或零件)有

m

个装配属性值，B(部件或零件)有

n

个装配属性值，构建数据驱动选配模型挖掘

m

个装配属性值与

n

个装配属性值之间的关联关系，使得在装配开始前，可将A的

m

个装配属性值作为数据驱动选配模型的输入，对待选配的B的

n

个装配属性值进行预测。根据预测结果，在B中选择相应零部件与A进行装配，使零部件选配一次成功，避免了由试凑法反复装拆调整而造成的精度下降，提高了装配的效率和装配质量的一致性。

图1 陀螺零部件选配流程示意图Fig.1 The selective assembly flow chart of gyro parts

2 基于Stacked-GRU网络数据驱动的陀螺零部件选配模型构建

基于数据驱动的动力随动陀螺零部件选配方法的关键在于数据驱动模型的构建，本文建立了Stacked-GRU网络数据驱动模型以指导陀螺零部件的选配，技术流程如图2所示。本节在介绍了基础的GRU网络之后，建立了Stacked-GRU网络数据驱动选配模型，并对Stacked-GRU网络数据驱动选配模型进行了详细介绍。

图2 基于Stacked-GRU的网络数据驱动陀螺零部件的选配流程示意图Fig.2 The selective assembly flow chart of gyro parts based on stacked-GRU network data driven model

2.1 门控循环单元(GRU)

门控循环单元(GRU)网络是循环神经网络(Recurrent Neural Network，RNN)的一种变体，通过引入门控机制来改进循环神经网络中的长距离依赖问题，具备信息学习长期依赖能力，能够有效解决简单循环神经网络梯度消失和梯度爆炸的问题，其单元结构如图3所示。

图3 GRU的结构示意图Fig.3 The structural diagram of GRU

图3中，

x

(

t

)、

h

(

t

)、

r

、

z

、

c

分别表示

t

时刻GRU单元的输入、输出、重置门、更新门与短期记忆，

σ

为sigmoid激活函数，⊗为向量元素乘积，⊕为向量和。更新门

z

的取值为0～1，

z

越接近1，记忆下来的信息越多。

z

值决定了上一单元记忆信息的保留数量。重置门

c

将新的输入与上一单元的记忆信息进行了结合。GRU单元的更新公式如式(1)～式(4)所示

z

=

σ

(-1+)

(1)

=

σ

(-1+)

(2)

=tanh((-1⊗

r

)+)

(3)

=(⊗)+((1-)⊗-1)

(4)

式中,

t

、

t

-1指的是

t

时刻与前一时刻，、、、、、为可训练权重层。

2.2 Stacked-GRU网络数据驱动选配模型的构建

通过堆叠多个GRU形成更深的Stacked-GRU网络，以获得更好的特征提取能力。本文在传统的GRU网络基础上，建立了Stacked-GRU网络数据驱动陀螺零部件选配模型，模型如图4所示。

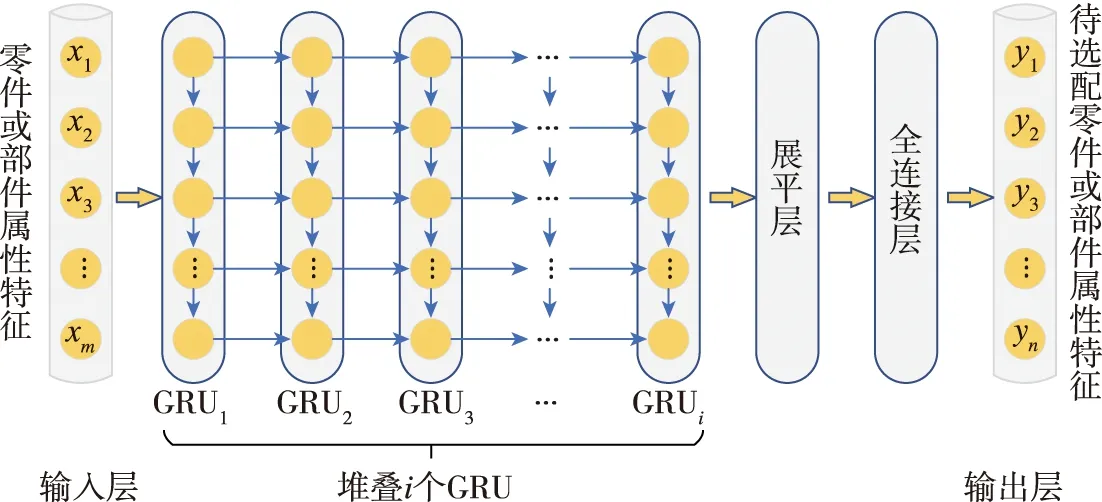
图4 基于Stacked-GRU网络数据驱动陀螺零部件选配模型示意图Fig.4 The gyro parts selective assembly schematic diagram of data driven model based on stacked GRU network

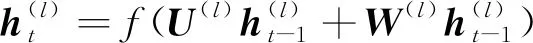
(5)

(6)

通过Stacked-GRU网络数据驱动模型指导陀螺零部件的选配，有利于减少陀螺在装配过程中的无效装配，提高装配效率。

3 实例验证与分析

本文实验操作平台为Windows10，工具为Python，所开发的神经网络是在Keras框架下搭建的。本节对实验数据进行了描述，设置了所开发网络的超参数，并对实验结果进行了分析与讨论。

3.1 实验样本

本文以动力随动陀螺典型的零部件装配——陀螺转子与调漂螺钉装配为例，进行了实验，两者的装配简图如图5所示。陀螺零部件材料分布不均、加工误差等因素的存在，使得陀螺转子的质心偏移了其旋转轴，导致陀螺漂移性能变差，无法对目标进行精确追踪。通过在陀螺转子顶部位置装配合适的调漂螺钉，能够调整陀螺转子的质心位置，使其尽可能落在其旋转轴上，以改善陀螺的漂移性能。调漂螺钉除长短不同外，其余的属性一致，在装配参数上使用调漂螺钉质量这一参数来进行表征。

图5 陀螺转子与调漂螺钉装配示意图Fig.5 The assembly diagram of gyro rotor and drift adjusting screw

选择不同质量的调漂螺钉与陀螺转子进行装配，实际上是根据陀螺零部件装配误差、陀螺转子质量分布不平衡量等参数进行选择的。然而，由于测量成本高以及测量难度大，难以对每一个装配误差值等参数进行精确测量。目前，装配人员根据从陀螺漂移测试中获取的+

X

、+

Y

、+

Z

、-

Y

、-

Z

五个方向的漂移最大值选择不同质量的调漂螺钉与陀螺转子进行装配，直至选配的调漂螺钉使陀螺转子的漂移性能能够满足要求为止。否则，需要进行拆解，重新选择调漂螺钉进行装配与漂移测试，陀螺转子装配调漂螺钉前后的漂移测试结果如图6所示。

(a)陀螺转子漂移值(装配前)

因此，本文的实验数据集由陀螺转子在+

X

、+

Y

、+

Z

、-

Y

、-

Z

五个方向上的漂移最大值与调漂螺钉质量共六项参数组成，并在实际装配中收集了528个陀螺装配样本用于本文分析。同时，将装配样本按4∶1的比例随机划分成了训练集与测试集。本文将陀螺转子在五个方向上的漂移值作为Stacked-GRU网络的输入，对调漂螺钉质量进行了回归预测。根据预测结果，指导了陀螺转子与调漂螺钉的选配。对于回归任务而言，期望预测值与实际值的差距越小越好。因此，实验评价指标采用了平均绝对误差(

E

)与根均方误差(

E

)，如式(7)、式(8)所示

(7)

(8)

3.2 超参数设置

对于神经网络而言，目前仍无针对超参数(如隐藏层数、隐藏层节点数等)的公认的设置与优化方法。考虑到本文训练的样本量有限，可以借鉴一些超参数设置的经验性建议进行设置。实验还进行了多组对比实验。其中，GRU为传统单层GRU神经网络模型，ANN为传统人工神经网络模型。ABR为自适应增强回归(Adaptive Boosting Regression，ABR)模型，它是集成学习的典型模型之一。各神经网络模型的超参数设置如表1所示。此外，在对比模型ABR中，设置基学习器为分类与回归树(Classification and Regression Trees,CART)。同时，采用线性损失，设置学习率为1，最大迭代次数为50。其中，在基学习器中设置决策树的最大深度为3，在内部节点中划分最小样本数为2，再划分叶子节点最小样本数为1。

在表1中，3指的是在ANN中，隐藏层采用3层全连接层堆叠形成，而不是GRU层。

表1 神经网络模型参数设置Tab.1 The parameters setting of neural networks

3.3 实验结果与分析

本节展示了数据驱动模型的实验结果，并对实验结果进行了讨论与分析。在实验开始前，对样本数据进行了标准化处理，消除了由各装配参数因量纲与取值范围不同而带来的影响。进行了多种不同方法的对比实验。在对比实验中，神经网络模型的参数保持了一致。同时，为消除随机性对实验的影响，每组实验各进行了10次，得到的实验结果如表2、表3以及图7所示。

表2 调漂螺钉质量预测结果对比Tab.2 Comparison of the mass of drift adjusting screws prediction results

表3 部分调漂螺钉质量预测结果Tab.3 The partial prediction results for the mass of drift adjusting screw

图7 部分调漂螺钉质量预测结果对比Fig.7 Comparison of the partial prediction results for the mass of drift adjusting screw

表2中，标注加粗部分为实验最优结果，表3则给出了部分调漂螺钉质量的预测结果。从表2的实验结果可以看到，由本文所提的Stacked-GRU数据驱动模型得到的实验结果最优，其平均绝对误差与根均方误差均是最优的。与传统GRU网络相比，本文所提方法的平均绝对误差与根均方误差分别降低了1.50%、1.70%，这说明所提的Stacked-GRU模型的预测精度更好。其中的原因在于，通过堆叠更多的GRU、构建更深的网络，能够提取更多的装配参数特征，进而具备更好的预测能力。与传统的人工神经网络(ANN)相比，所提方法具备信息记忆能力，能够更有效地捕捉到陀螺转子装配参数之间与调漂螺钉装配参数之间的关联关系，其平均绝对误差与根均方误差分别降低了57.19%、49.48%，预测精度明显优于传统人工神经网络；同样地，传统GRU网络的预测精度优于传统的人工神经网络，也体现出了这一点。在训练样本有限的情况下，浅层的机器模型具备优良的预测性能表现，这也是ABR能够具备较好的预测能力的原因。即便如此，本文所提方法的平均绝对误差与根均方误差仍然优于ABR，这表明了本文所提方法的有效性。

结合表2、表3、图7的结果可以看出，虽然所提方法得到的实验结果最优，但仍有部分装配样本的调漂螺钉质量值的预测误差较大。这其中的原因在于，针对所选配的调漂螺钉的质量，没有一个明确的量化评价指标，只要求其在装配后满足性能要求即可，因此调漂螺钉的质量可以在一定范围内波动；另一方面，是神经网络的训练样本有限，对装配参数的一些细微特征难以进行有效的捕捉，而通过进一步增加训练样本，可有效提升模型的预测精度。

本文在神经网络训练过程中，采用平均绝对误差作为损失函数(如式7所示)对模型进行了优化，得到所提方法最优模型的损失曲线变化趋势如图8所示。从图8可以看到，随着迭代次数的增加，模型损失值逐渐减小并趋于收敛，这表明所提模型具备很好的预测能力。图9与图10分别展示了所提方法最优模型调漂螺钉质量预测结果的相对误差值及其相对误差分布直方图。

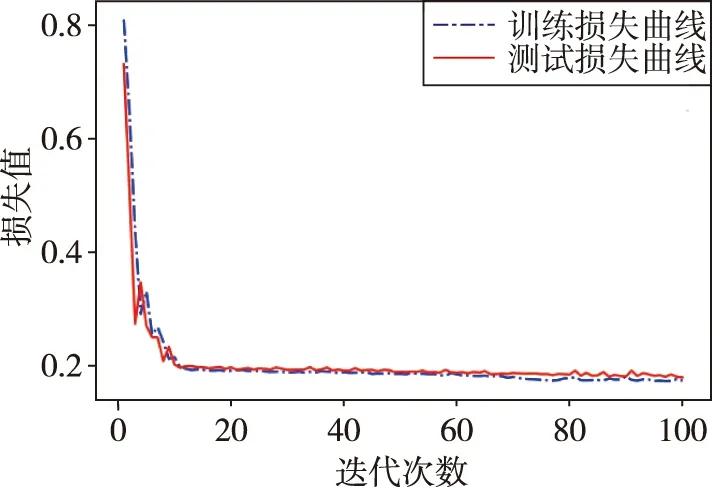
图8 Stacked-GRU网络最优模型损失曲线变化趋势Fig.8 The loss curve variation trend of the best stacked GRU network

图9 调漂螺钉质量预测结果的相对误差值Fig.9 The relative error value of prediction results for the mass of drift adjusting screw

图10 调漂螺钉质量预测结果相对误差分布直方图Fig.10 The prediction results relative error distribution histogram for the mass of drift adjusting screw

从图9、图10可以看出，本文所提的Stacked-GRU网络在测试集上的预测结果的相对误差值均在较小范围内，且绝大部分在5%以内。由于允许调漂螺钉质量在一定范围内波动，即使调漂螺钉质量预测值与实际值存在误差，也可满足实际装配的要求，这说明所提方法具备很好的预测能力。通过所提方法对调漂螺钉质量进行回归预测，能够实现陀螺转子与调漂螺钉的选配。

4 结 论

本文分析了动力随动陀螺在其装配过程中存在的零部件一次装配成功率低的问题。为提高陀螺零部件的装配效率，提出了一种基于Stacked-GRU网络数据驱动的陀螺零部件选配方法。该方法在传统GRU网络的基础上，通过堆叠更多的GRU层、构建了更深的网络，以提取更多、更丰富的陀螺装配参数特征，提高了预测精度。以陀螺转子与调漂螺钉装配为例，验证了所提方法的预测结果能够有效指导陀螺零部件的选配，且预测精度优于传统的GRU网络、传统的人工神经网络。

本文建立的Stacked-GRU网络数据驱动选配方法克服了传统选配方法对高精度测量技术的过度依赖。根据装配参数，所提方法可实现陀螺零部件的精确选配，可有效避免由测量成本高而导致的生产成本高的问题，提高企业的生产效益。同时，本文所建立的Stacked-GRU网络数据驱动模型对复杂精密产品零部件的选配具有较好的适应性，其创新性地将人工智能技术引入到了复杂精密产品的装配中，有效解决产品因人工装配经验不足而导致的反复装配调整工作，以及产品装配精度下降的问题，具有良好的工程应用价值。此外，本文所提的数据驱动选配方法也为复杂精密产品零部件的选配提供了一种新的解决方案，有助于提高复杂精密产品的自动化生产水平，实现复杂精密产品制造模式的升级。