多种数据结构实现迷宫问题详解

章丽玲

(湖北第二师范学院 计算机学院，武汉 430205)

迷宫问题是“数据结构”课程中经典的非数值型的程序设计问题，理解迷宫问题的不同解决思路，对掌握《数据结构》课程的核心知识点具有非常重要的意义，本文将采用几种典型的数据结构，利用不同的算法来实现迷宫问题。

1构造迷宫

用一个二维数组mg[M+2][N+2]表示迷宫，如图1所示，M=8，N=8，状态为0时表示对应方块是通道(可走)，状态为1时表示对应方块是障碍物(不可走)，为了算法方便，一般迷宫的外围加一条围墙。设定入口为mg[1][1]，出口为mg[8][8]。

图1 迷宫图

2 算法思路

求解迷宫问题通常采用“穷举探索求解法”，即从入口出发，顺某一方向向前探索，若能走通，则继续往前走，否则沿原路退回(回溯)，换一个可行的方向再继续探索，直至所有可能的通路都探索到为止。为了保证在任何位置上都能原路退回，常用的数据结构有栈和队列，如果把迷宫中的每一个位置看作是一个点的话，那么就可以把迷宫转换为一个个相连或分断的各个顶点之间的关系，因此，可以使用另一种数据结构——无向图来表示。下面将针对不同的数据结构来实现迷宫问题。

2.1 用栈实现迷宫

栈是一种只能在一端进行插入和删除操作的线性表。允许进行插入和删除操作的一端称为栈顶(top)，另一端称为栈底(bottom)。栈的主要特点是后进先出，正是栈的这一特点使得它成为解决迷宫问题的数据结构。

2.1.1 数据结构设计

采用顺序栈实现迷宫，迷宫栈声明如下：

typedef struct

{

int i; //当前方块的行号

int j; //当前方块的列号

int di; //di是下一相邻可走方位的方位号

}Box;

typedef struct

{

Box data[MaxSize]; //栈中每一个结点存放i,j,di.

int top;

} StType;

2.1.2 栈实现的算法设计思路

对于迷宫中的每个方块，有上、下、左、右四个方块相邻，如图2所示，第i行第j列的当前方块的位置记为(i,j)，规定上方方块为方位0，并按顺时针方向递增编号。在试探过程中，按从方位0到方位3的方向查找下一个可走的相邻方块。为了保证在任何位置上都能沿原路退回(称为回溯)，需要保存从入口到当前位置的路径上走过的方块，若一个非出口方块(i,j)是可走的，将它进栈，每个刚刚进栈的方块，其方位di置为-1(表示尚未试探它的周围)，然后开始从方位0到方位3试探这个栈顶方块的四周，如果找到某个方位d的相邻方块(i1,j1)是可走的，则将栈顶方块(i,j)的方位di置为d，同时将方块(i1,j1)进栈，再继续从方块(i1,j1)做相同的操作。若方块(i,j)的四周没有一个方位是可走的，将它退栈，继续其他的路径。实际上，该算法思路是利用栈的后进先出的特点，一步一步地查找可走的方块，直到找到出口为止，该方法类似于图的深度优先搜索方法。

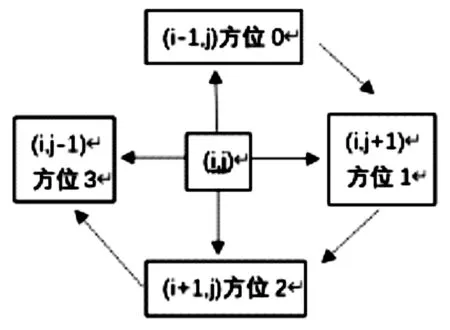
图2 迷宫方位图

2.1.3 算法描述

Bool mgpath(int xi,int yi,int xe,int ye) //求解路径为(xi,yi)->(xe,ye)

{

将入口(xi,yi)进栈(其初始方位设置为-1);

mg[xi][yi]=-1;

while(栈不空)

{

取栈顶方块(i,j,di);

if((i,j)是出口(xe,ye))

{输出栈中全部方块构成一条迷宫路径；

return true;}

查找(i,j,di)的下一个相邻可走方块；

If(找到一个相邻可走方块)

{该方块为(i1,j1)，对应的方位为d；

将栈顶方块的di设置为d;

(i1,j1,-1)进栈；

mg[i1][j1]=-1;}

if(没有找到(i,j,di)的任何相邻可走方块)

{将(i,j,di)出栈；

mg[i][j]=0; }

}

return false;

}

2.2 用队列实现迷宫

队列也是一种操作受限的线性表，其限制为仅允许在表的一端进行插入操作，而在表的另一端进行删除操作。进行插入的一端称为队尾(rear)，进行删除的一端称为队首(front)。队列的主要特点为“先进先出”，可以利用队列的这个特点来实现迷宫问题。

2.2.1 数据结构设计

采用顺序队列qu保存走过的方块，这里不使用循环队列，因为在找到出口时需要利用队列中的所有方块查找一条迷宫路径，因此要求顺序队列qu有足够大的空间。

typedef struct

{ int i,j; //方块的位置

int pre; //本路径中上一方块在队列中的下标

} Box; //方块类型

typedef struct

{

Box data[MaxSize];

int front,rear; //队头指针和队尾指针

} QuType; //顺序队类型

2.2.2 队列实现算法设计思路

首先将入口(xi,yi)进队，在队列qu不为空时循环，出队一个方块e，其下标为front，然后查找方块e的所有相邻可走方块，假设e1和e2两个方块，将它们进队，它们在队列中的位置分别是rear1和rear2，并且将他们的pre均设置为front，当找到出口时，通过出口方块的pre值前推找到入口，所有经过的中间方块构成一条迷宫路径。实际上，该算法思路是利用队列的特点，一层一层向外扩展查找可走的方块，直到找到出口为止，该方法类似于图的广度优先搜索方法。

2.2.3 算法描述

Bool mgpath1(int xi,int yi,int xe,int ye)

{

将入口(xi,yi)的pre置为-1并进队；

mg[xi][yi]=-1;

while(队列qu不空)

{出队一个方块e，其在队列中的位置是front;

if(方块e是出口)

{ 输出一条路径; return true;}

for(对于方块e的所有相邻可走方块e1)

{ 设置e1的pre为front;

将方块e1进队；

将方块e1的迷宫数组值设置为-1;}

}

return false;

}

2.3 用图搜索方法实现迷宫

图都是由顶点和边构成的，可以把迷宫图中的每一个方块看成一个顶点，方块和方块之间的连通性看出顶点与顶点的边，因此，可以把迷宫问题看成图的问题，可采用图的深度优先搜索和广度优先搜索算法来求解迷宫问题。

2.3.1 图的数据结构设计

常用的图的存储结构有邻接矩阵和邻接表。这里采用邻接表比较好，因此首先需要将迷宫图的二维矩阵转化为对应的邻接表，其思路为：一个方块看成一个顶点，编号为(i,j)，根据周围4个方向状态为0的方块建立邻接表，邻接表的头结点是一个二维数组。对应的邻接表类型声明如下：

typedef struct Anode

{ int i,j;

Struct Anode *nextarc;

} ArcNode; //边节点类型

typedef struct Vnode

{ ArcNode *firstarc; //指向第一个相邻可走方块

} VNode; //头结点

typedef struct

{ VNode adjlist[M+2][N+2];

} AdjGrapgh;

Typedef struct

{ int i;

Int j;

} Box; //定义方块

Typedef struct

{ Box data[MaxSize];

Int length;

} PathType; //定义路径类型

邻接表的表头用一个二维数组adjlist表示,adjlist[i][j]仅含有一个firstarc指针，它指向方块(i,j)的四周可走方块构成的一个单链表，图一对应的迷宫邻接表如图3所示。

图3 迷宫邻接表

2.3.2 算法设计

在搜索迷宫路径时可以采用DFS(深度优先搜索)或者BFS(广度优先搜索)算法，将访问标记数组改为visited[M+2][N+2]，入口作为初始顶点，结束条件为找到出口。下面算法采用的深度优先搜索算法求(xi,yi)到(xe,ye)的所有路径。

Void FindPath(AdjGraph *G,int xi,int yi,int xe,int ye,PathType path)

{ ArcNode *p;

visited[xi][yi]=1; //入口置已访问标记

入口加入路径，并将路径长度加一

If(xi==xe && yi==ye) //找到出口

{ 输出迷宫路径； }

p=G->adjlist[xi][yi].firstarc;//p指向顶点v的第一条边顶点

//采用递归的方法深度优先搜索

while(p!=null)

{ if(visited[p->i][p->j]==0)

FindPath(G,p->i,p->j,xe,ye,path);

P=p->nextarc;

}

visited[xi][yi]=0;

}

3 小结

线性表、栈、队列、递归、图、深度优先搜索(DFS)和广度优先搜索(BFS)属于“数据结构”课程的核心知识点，他们既是教学重点，又属于教学难点，然而，通过求解迷宫问题，可以把这些知识点串在一起，使学生能够灵活地应用线性表解决实际问题，分清栈和队列应用的区别，为了拓展学生的逻辑思维，将迷宫问题描述成图的搜索问题，可采用深度优先搜索的递归思想和广度优先搜索的非递归思想来实现。总之，采用多种数据结构来实现迷宫问题可大大提高学生对数据结构核心知识点的理解深度，提高学生对迷宫算法的多维性理解能力。