基于改善的射线相交法快速计算复杂几何距离场
2021-10-25周红梅秦歌张小明荆双喜
周红梅,秦歌,张小明,荆双喜
(1.河南理工大学 机械与动力工程学院,河南 焦作 454000;2.广东新环机电装备制造有限公司 博士后创新基地,广东 中山 528429)
0 引言
离散的有符号距离场定义为每个三维栅格点到模型表面的最短距离值构成的一个标量场。距离场主要应用到构造实体几何显示、补洞、法矢估计和表面重构[1]、骨架及中轴提取[2-3]、碰撞检测和路径规划、变形和动态模拟、纹理映射、布尔操作、路径规划和导航等方面。最基础的距离场计算方法是直接计算空间任意点到几何模型的最小距离值,显然针对不同几何模型其计算方法也不同。通常几何模型的描述方法是多样的,可采用隐函数法、参数化法、网格法(三角形或多边形网格)、数据点云和体数据等。不同方法描述的几何模型也可以通过一系列的操作相互转换[4],例如由传统几何模型向体数据转化的方法、参数化方法向隐函数法转换的方法,采用Voronoi[5]图和Delaunay三角剖分的方法可将数据点云转化为网格化模型。对隐函数法描述的几何模型,只需要沿着x,y,z3个轴方向搜索,计算每个栅格点上的距离场值。对于三角网格描述的三维几何体[6-7],最基础的方法是根据点投影到每个三角网格所在平面的位置计算最短距离值,而要计算每个点到每个三角网格的最短距离存储最小值作为距离值,显然用该方法费时费力,为了减小计算量,可将原始的三角网格模型用空间数据结构存储,如BSP树、八叉树等,这样就可以尽快地查找距离所求点最近的三角形。
若对象是数据点云,计算距离场最直接的方法是由H.Hoppe等[1]提出的:首先为每个数据点计算其切平面;其次通过法矢调整使切平面法矢方向一致;最后通过邻域搜索到离采样点最近的点并计算法矢,从而求得有符号距离值。对于海量数据点云,整个过程计算量较大,计算效率比较低。除了上述对距离场精确的计算,还可以采用近似的计算方法,ZHAO H K等[8]采用迎风高斯-赛德尔迭代求解Eikonal方程,通过反复迭代计算可以获得逼近的距离场值。二维有符号距离场计算关键的一步是判断点的位置,也就是判断其符号。最常见的点多边形问题求解是采用多边形的点包容性检测(point-in-polygon test)[9-13]。通过从被测点向某方向作一条射线,计算该射线与多边形的边交点个数进行判定。若有奇数个交点,则该点位于多边形内;否则位于多边形外。这种方法简单直观,可处理任意多边形,通常被用作与其他算法对比的基准算法。YANG S等[9]提出quasi-closest point概念,用以表示受约束条件限制的最近点,并根据quasi-closest point获得被测点的属性,避免了当一个顶点的两条邻边几乎共线时,使用顶点的凹凸性判定而导致的错误。凸剖分法[11]先将多边形凸剖分,并以树结构管理所得的凸多边形,判定时通过树结构快速查找可能包含被测点的凸多边形,然后以高效的凸多边形点检测算法确定被测点是否在多边形内。该方法的判定计算时间复杂度O(logN),是目前多边形点检测问题最低的判定计算时间复杂度。当剖分得到的凸边形个数较少时,该算法具有很高的效率,但随着凹点数目的增多,凸多边形数目随之增多,检测时间也会增加。
本文提出的新算法基于均匀网格结构,采用改善的射线相交法进行符号判断。从每个栅格点引出一条射线与窄带内的数据集相交,通过判断交点数量来判断该栅格点在模型的位置。该方法只需要判断交点的数量,不需要进行交点的计算,且该方法的时间复杂度远低于O(N)。
1 方法描述
本文通过改善的射线相交法计算二维复杂几何数据点集的有符号距离场,计算流程如图1所示。首先,通过扫描或者采样二维模型获得二维数据点集;其次,将该数据集调整为有序的封闭数据集,将其均匀子分到指定的分辨率;针对每个栅格点,可以通过领域搜索算法快速计算无符号距离场;最后,通过改善的射线相交法获得每个栅格点的符号值。

图1 距离场计算流程图Fig.1 Flowchart of distance field computation
1.1 无符号距离场
作为描述散乱数据点云的重要信息,距离函数可以显示任意散乱数据集S的内在性质,且大部分的三维重建方法中,距离函数都是其算法操作的基础,因此它直接决定了最终曲面几何精度和拓扑结构的准确性。有符号距离场是指空间任一点p到曲面、曲线或点集S的含符号的距离值所构成的空间场模型,它包括两部分:一是p与S中的最近点xi之间的距离值;二是该距离值的符号。通过判断p位于S的哪一侧确定其符号,即
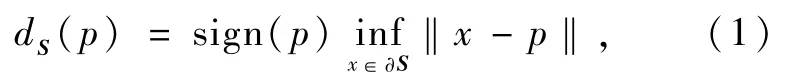
式中,如果p在S外,sign(p)取为1,否则sign(p)取为-1。
首先获取物体中所有点的最大与最小坐标值为{xmin,xmax,ymin,ymax},给定一个容差值σ,则两个坐标方向划分的栅格间距为
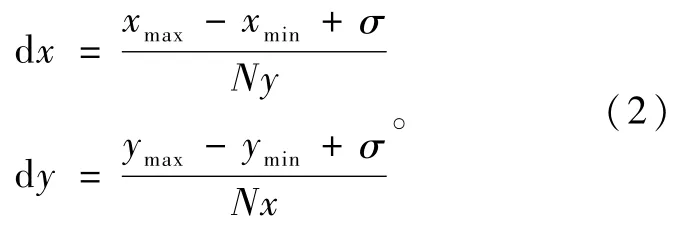
无符号距离值容易计算,但是对大的数据集计算也会耗费计算时间,对于栅格尺寸为(Nx×Ny)的每个栅格点,需要计算点集S中的每个数据点到栅格点的距离,然后取最小值。直接计算法复杂度为O(N×Nx×Ny),可以采用领域搜索法提高计算效率。为了计算距离场,给出下列定义。
定义1.1 每个节点包含4个顶点和4条边。顶点和边信息添加到节点信息里面。如图2所示,节点A被定义为Node(3,2),对于划分Nx×Ny分辨率尺寸,节点总数为(Nx-1)和(Ny-1)的乘积。
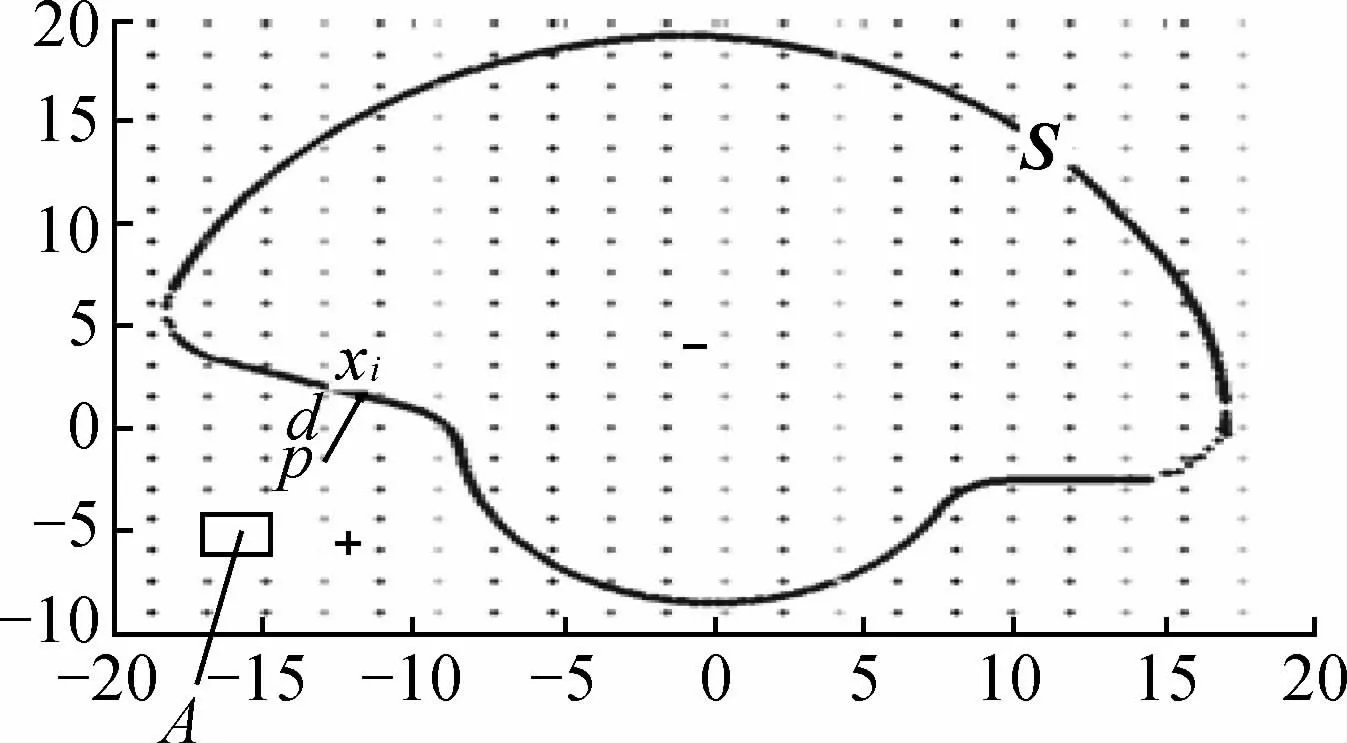
图2 二维有符号距离场(20×20)Fig.2 2D signed distance field(20×20)
定义1.2 在符号判断过程中,模型外部的节点被定义外部节点,模型内部的节点被定义为内部节点,和模型相交的节点被定义为边界节点。当前,通过判断点集的位置可以直接获得边界节点,如图3所示。

图3 边界节点Fig.3 Boundary node
1.2 改善的射线相交法
判断有符号距离场符号的方法最早是H.Hopper[1]提出的表面法矢估算法。然而,该方法对点云的噪声敏感且针对密集数据点云计算量大。法矢调整计算复杂度为O(N2)。对于二维数据点集,最常用的方法就是射线相交法。通过引出一条射线计算其交点的数量来判断该点与数据点集的关系,类似于点在多边形内测试法[9-11]。改善的射线相交法实施步骤如下。
步骤1首先,一个复杂模型被扫描或采样获得二维数据集S。如果输入的是有序的数据集,直接进入步骤2;否则,数据集被调整成有序的封闭集。
步骤2用一个包围盒包围该数据集,均匀子分该包围盒到指定的合适的分辨率(Nx×Ny)。于是节点总数为(Nx-1)×(Ny-1)。每个节点包含四个顶点(i,j),(i,j+1),(i+1,j),(i+1,j+1)。所有顶点被储存到相应的节点内容。所有(Nx-1)×(Ny-1)个节点被访问,包含数据点的节点被标记为边界节点(图3),其他节点被设置为未定义。该操作的完成时间为O((Nx-1)×(Ny-1))。
步骤3对于每个栅格点Pg(图4的栅格点B,三排六列),设它的坐标为(x0,y0),找出窄带(x>x0且y0-r≤y≤y0+r)范围内的所有点,其中r为预先定义的栅格间距,本文中r=dy。定义这些点的数量为nn,显然nn<<N,计算复杂度远远小于O(N)。这些点设为集合PX,为PX排序为连续的点PX1,PX2,...,PXnn。
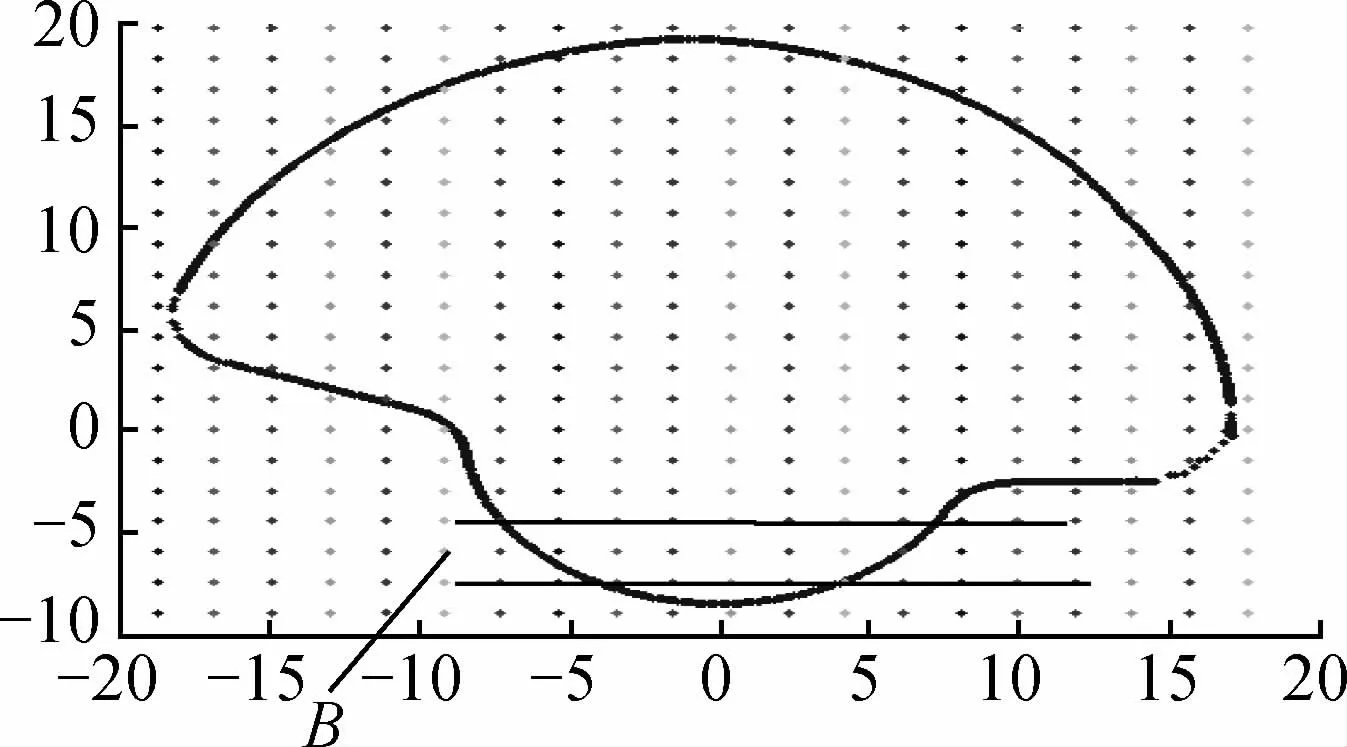
图4 查找窄带范围内的所有点Fig.4 Finding out all points in the narrow band
步骤4向x正向构造一条通过Pg的射线,计算这条射线与PX的交点。如图5所示,可能有5种相交情况,其中(x1,y1)和(x1,y2)是PX内相邻点的坐标。相交情况取决于(x0,y0),(x1,y1)和(x2,y2)。(xj,yj)是交点坐标。

图5 不同相交情况Fig.5 Different Intersection cases
步骤5如果交点总数为奇数,该栅格点Pg被判断为内部点,返回负值,否则,栅格点Pg被判断为外部点,返回正值。继续下一个栅格点,继续步骤3。
距离场被划分后,扫描所有离散的栅格顶点,依据1.1节的定义,评判规则如下。
(1)所有的外部节点的顶点被标记为正,所有外部节点的4条边被定义为外部边。
(2)如果一个节点不包含任何数据集,而且至少其中的一个顶点为外部顶点,该顶点应为外部节点。
(3)如果一个节点包含数据,且至少一个顶点为内部顶点,标记为负,至少一个顶点为正。
通过上述改善的射线相交法,能获得栅格点的所有符号,如图6所示,“+”表示距离值为正,“o”表示距离值为负或零。然后依据上述规则,把所有的节点分为3种:外部节点(黑色),边界节点(红色)和内部节点(白色),如图7所示。
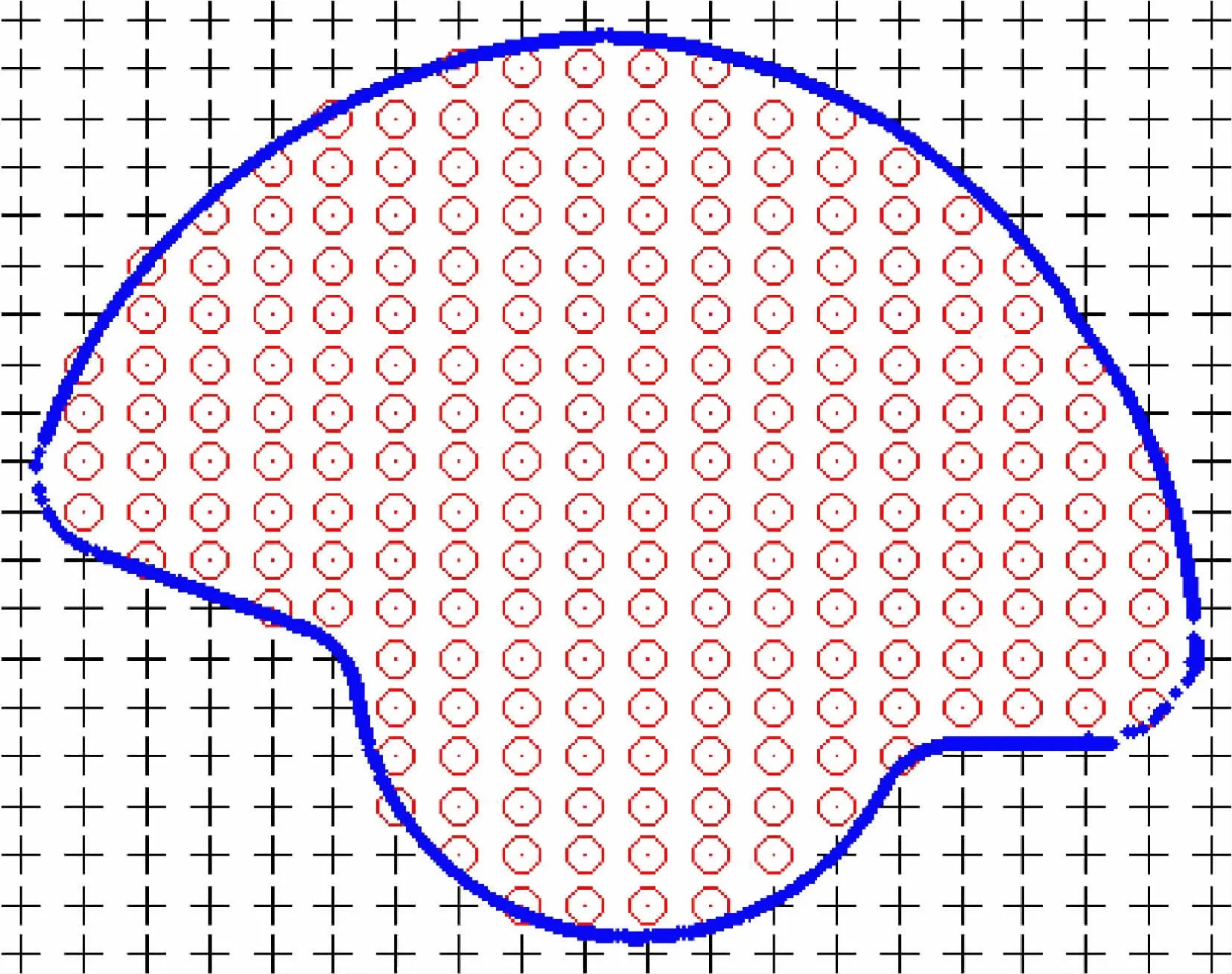
图6 符号判断Fig.6 Sign judgment

图7 外部(黑色)、内部(白色)和边界节点(红色)Fig.7 Exterior,interior and boundary node
2 实例
通过上述改善的射线相交法,能够计算有符号距离场的等值线,然后采样等值线来计算其精度。为了对方法的性能进行评估,通过对3个工程模型在不同分辨率下的计算精度和计算时间进行比较,结果如表1所示。所有程序在3.6GHz intel(R)Core,8 GB of RAM上运行。通过表1可以看出,分辨率高的情况下用时较多,而计算时间与模型复杂度和数据集数量相关度不大。图8列出了采样等值线与原数据集的比较。图9为不同模型不同栅格尺寸的符号判断结果。
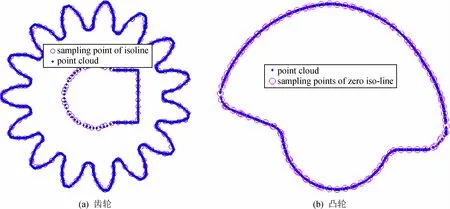
图8 数据集与等值线采样点比较Fig.8 The comparison of dataset with sampling point of isoline

图9 符号判断结果Fig.9 Sign judgment results

表1 不同数据集不同分辨率网格下用时精度比较Tab.1 Time and precision for different datasets with variable grid resolution
3 结论
本文提出了一种新的复杂二维数据集的快速距离场计算方法,采用改善的射线相交法进行符号判断。算法从每个栅格点引出一条射线与窄带内的数据集相交,通过判断交点的数量来判断该栅格点在模型里的位置。该方法只需要判断交点的数量,不需要进行交点的计算。最后通过一些工程实例验证了该方法的有效性和精确性。结果显示,该方法不仅适用于一些光滑的结构,而且也适用于齿轮这种凹凸结构模型,对其三维数据集可以先切片成二维模型,再进行计算。
