公路填石路基压实工艺优化方法及效果评价
2021-10-25李盛田文迪刘玉龙郜梦棵
李盛,田文迪,刘玉龙,郜梦棵
(1.长沙理工大学交通运输工程学院,湖南长沙,410114;2.中交四航局第二工程有限公司,广东广州,510230)
随着我国公路网不断扩大,山区高速公路建设得到迅速发展。很多山岭重丘地区存在各类岩性石料,深挖路堑和隧道爆破产生的石料往往被弃用,造成资源浪费。填石路基作为山区高速公路建设必不可少的一部分,对废弃石料的利用率较高,经破碎处理后作为路基填料可实现就地取材,节约资源,降低工程造价,并可获得强度和稳定性高的路基[1-3]。填石路基与填土路基不同,其主要填料具有粒径较大、抗剪强度高、孔隙率大、透水性好等特点,是我国山区高速公路修筑的一种重要形式[4-5]。目前对填石路基的研究方法主要有即现场试验和室内振动压实试验[6-8]。现场试验对施工方法和施工工艺的要求较高;室内振动试验通常采用粒径均匀的石料,压实效果虽然理想,但与实际情况相关较大,从而造成试验结果不准确,并且室内试验在数据获取和处理上有一定难度,导致现场试验和室内振动压实试验难以揭示填石路基压实的细观过程。
如何根据填料的工程特性选择适宜的压实工艺,国内外学者进行了相关数值模拟分析。在研究颗粒振动压实中破碎机理方面,RUSSELL 等[9]将破碎准则运用到离散元中,模拟出较好颗粒受荷载后的真实破碎情况;CLEARY等[10]采用离散元法对填料破碎时粒径范围和破碎效率进行了数值模拟分析,研究了颗粒体内部结构在振动压实下的变形机理。在压实应力数值模拟方面,姜在田[11]结合现场试验建立碎石颗粒模型,在假设条件下对粗颗粒的压实过程进行数值模拟,明确了影响粗颗粒压实的关键因素;方磊等[12]采用随机离散单元法建立了石料颗粒结构模型,对影响填石路基的主要施工因素进行模拟,分析了激振力、振动频率对压实效果的影响;MIRMORADI等[13-15]使用2 种2D 类型应力建模研究模型的压实效应,并计算了有效应力。在采空区压实理论研究方面,朱广安等[16]利用FLAC3D软件开发了一套新的数值算法并用于某煤矿工作面开采全过程模拟;张村等[17]采用离散元数值模拟研究了采空区破碎煤岩压实在破碎的变化过程及颗粒破碎压实特征。目前针对填石路基压实工艺方面的研究总体较少,且采用的研究方法多为数值模拟,缺乏对研究结果的工程验证和修正。考虑数值模拟压实过程虽能较准确地分析颗粒压实过程中的动力响应,但成果能否应用于实体工程且应用效果如何还需进一步研究和完善,为此,本文作者通过数值方法定量分析压路机质量、激振力、振动频率和行驶速度对压实效果的影响,基于仿真计算得出不同压实参数下路基最大压应力、有效压实深度、路表沉降,初步确定提升压实水平和效率的优选压实工艺;依托某重载交通高速公路填石路基工程试验段进一步验证,确定优选压实工艺的合理性。
1 填石路基振动压实仿真模型的建立
1.1 振动压实原理
振动压实法是能保证填石路基压实质量的施工方法[18],所需压实机械主要是振动压路机。振动压路机在进行压实作业时,振动轮的振动会对填石路基表面施加往复冲击力,从而在石料内产生一系列冲击波,如图1所示。在冲击波作用下,被压实的石料由初始的静止状态变为运动状态,石料之间的摩擦力也由初始的静摩擦力逐渐变为动摩擦力。同时,由于水分的离析作用在石料外产生一层水膜,形成了石料运动的润滑剂,导致石料间的摩擦力显著下降,这为石料的运动创造了有利条件。石料在冲击波作用下的运动会改变石料的相对位置,出现石料相互填充的现象,因而,填石路堤的压实度提高,同时,石料之间的紧密接触也增大了摩擦力,使路堤的承载能力提高。
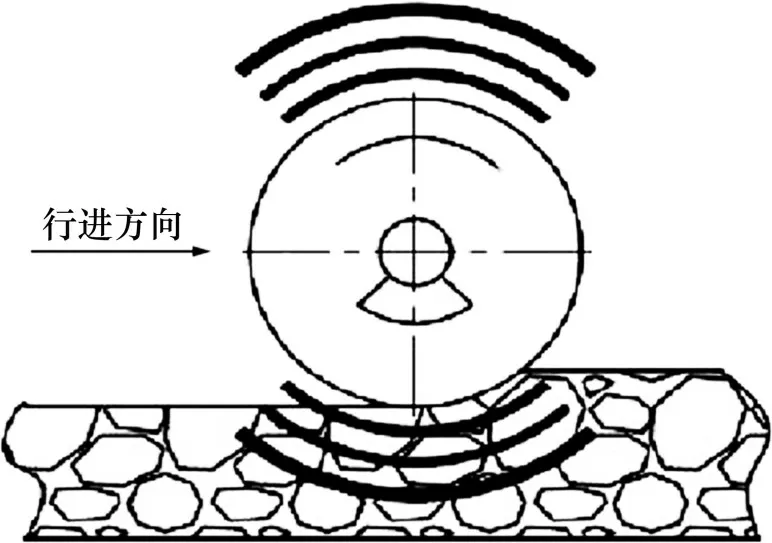
图1 振动压实原理示意图Fig.1 Principle diagram of vibrational
1.2 振动压实模型的建立
建立模型是数值模拟的第一步,确定土体的本构模型、采用的单元类型、网格划分及荷载等参数是关键[19-21]。将填石路基压实过程视作平面应变问题,采用平面应变模型,假定土基在水平方向和向下方向均为无限大,土基之上的填石结构层厚度为有限,但水平方向的填石结构层厚度为无限大。振动碾压有限元计算采用ABAQUS 有限元软件进行建模,建立长为20 m、高为10~40 m的二维数值模型,其中土基部分高度不小于20 m,其余为填石路基部分;在结构各个边界面施加相应的约束条件,模型底部施加完全约束,两侧施加水平方向约束,上表面不施加任何约束,为自由表面;压路机振动轮直径为1.6 m,振动轮与路基表面的接触面在行驶方向的长度为0.2 m。为提高计算效率和精度,整个数值模型均采用4节点缩减积分单元(CPS4R)模拟。建模完成后,采用Structure技术对路面结构划分网格。有限元模型及网格划分如图2所示。
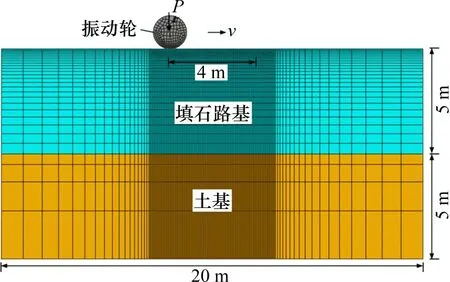
图2 有限元模型及网格划分Fig.2 Finite element model and meshing
路基填料和振动轮采用弹性本构模型,土基采用弹塑性本构模型,其物理力学参数参考依托工程的地质勘查报告和类似填石路基工程中的岩组物理力学性质指标建议值进行综合取值,如表1所示。在压实过程中,振动轮与填石路基之间保持接触状态,振动轮与填石路基表面之间采用摩擦型接触,摩擦因数为0.1。接触面只传递法向压力和切向摩擦力,振动轮不发生跳振现象。

表1 材料物理力学参数Table 1 Material physical and mechanical parameters
压路机荷载采用压力荷载形式,压路机振动轮作用在路基表面的振动荷载P计算式为

式中:P为振动轮作用在路基表面的总荷载,振动荷载示例如图3所示;G为振动轮重力;F0为压路机产生的激振力;ω为振动圆频率,ω=2πf(f为振动频率);t为时间。

图3 振动压路机振动荷载与时间的关系Fig.3 Relationship between vibration load of vibratory roller and time
由于采用的是均质材料,计算结果不受压路机行驶距离的影响,因此,考虑到计算效率,模拟压路机行驶距离4~6 m;碾压速度不影响荷载,但影响某位置土体受到冲击作用的持续时间,模拟设定行驶速度为2~4 km/h;在动力系统中仅考虑竖直方向的激振力。
1.3 压实工况及参数设置
为了定量分析压路机质量、激振力、振动频率和行驶速度等对填石路基压实效果的影响,对单振动轮轮重力、压路机产生的激振力、振动频率、行驶速度共4种参数各取2种常用水平,按不同参数与水平组合设计16种压实工况(见表2)进行数值模拟。以路基最大压应力、有效压实深度(压路机碾压作用下应力发生显著改变的填料深度)和路表沉降为指标对填石路基的单次压实效果进行评价,即对填石路基在压路机1次压实后的效果进行评价。

表2 数值模拟压实工况参数Table 2 Parameters of numerical simulation compaction conditions
2 填石路基振动压实仿真计算及优选压实工艺确定
2.1 振动压实动力响应计算分析
根据上述工况及参数设置,运用有限元软件模拟路基在振动压实过程中的动力响应情况。图4和图5所示分别为工况1条件下振动压实过程中路基的竖向应力云图和竖向位移云图。
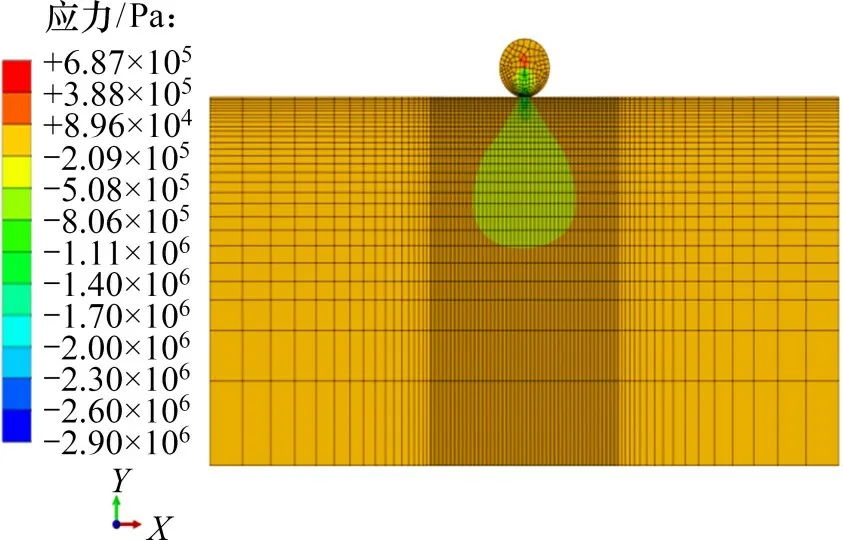
图4 竖向应力分布云图Fig.4 Cloud chart of vertical stress distribution
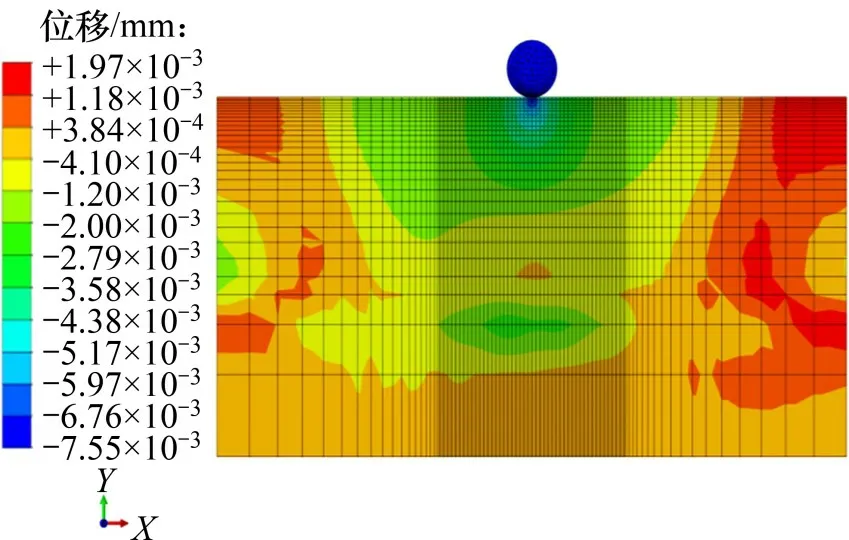
图5 竖向位移分布云图Fig.5 Cloud chart of vertical displacement distribution
由图4和图5可知:路基表面一定深度范围内的填料受到振动轮的明显冲击作用,其竖向应力明显增加,导致振动轮周围土体发生显著沉降,表明路基填料得到有效压实。填石路基不同次数的压实效果如表3所示。
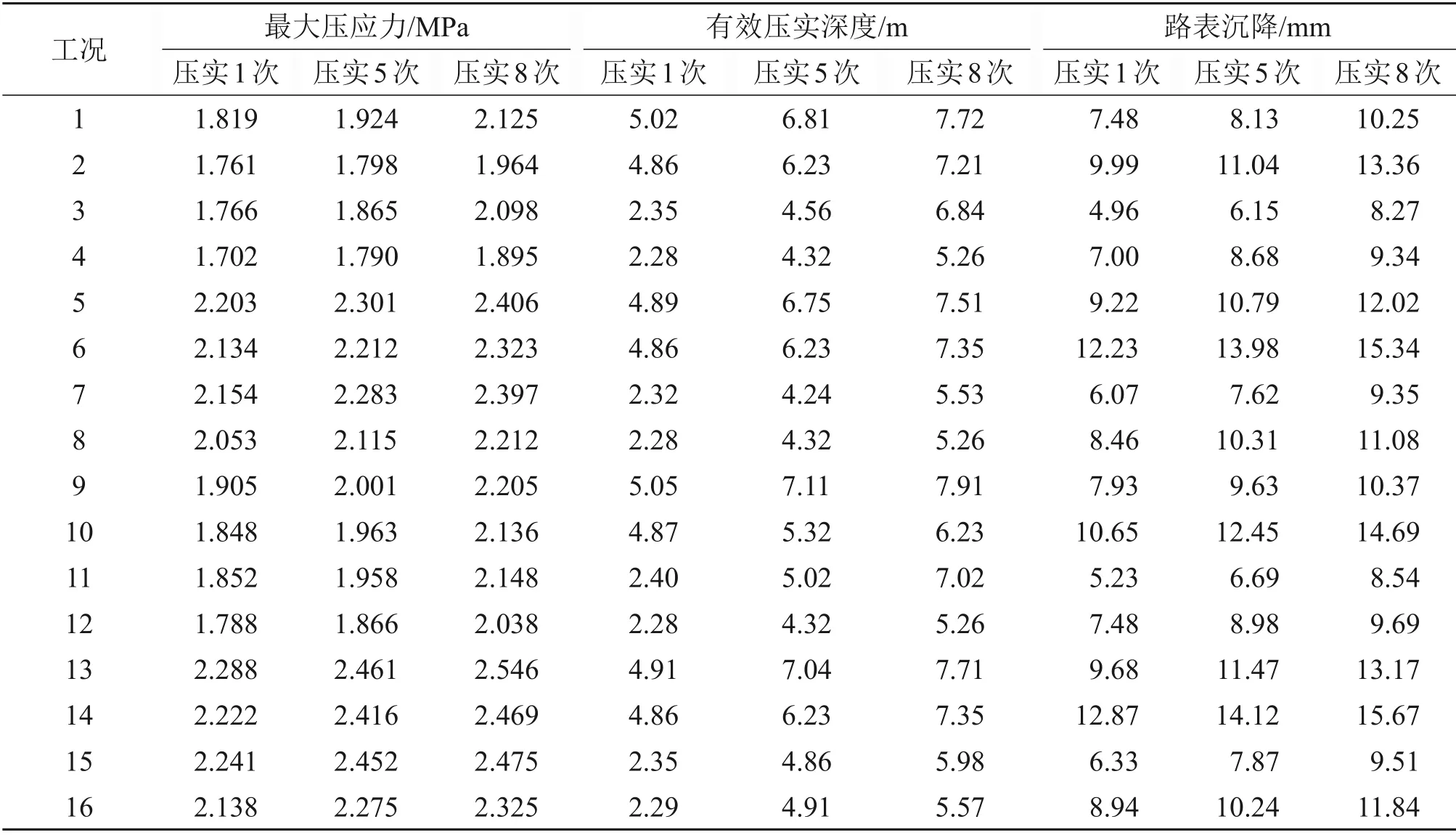
表3 不同压实次数数值模拟结果对比Table 3 Comparison of numerical simulation results of different times of compaction
2.2 优选压实工艺确定
经一定压实次数后,碾压对填料产生的嵌挤密实作用有限,考虑能耗和经济性并结合试验路段压实情况,确定最优压实遍数为8次时能达到较好压实效果。通过有限元分析计算得出各种压实工况下路基最大压应力、有效压实深度、路表沉降值,并进行排序,排序第一得1.0分,第二得0.9分,依次类推,最低取0.1 分,并将8 次碾压后所得路基最大压应力、有效压实深度和路表沉降这3项各自排序得分相加,得分最高的工况为优选工况,当分值相同时,以路表沉降的排序来确定优选工况;若路表沉降相同,则按路基最大压应力的排序来确定;若路基最大压应力也相同,则按有效压实深度排序来确定优选工况。各工况得分情况见表4。
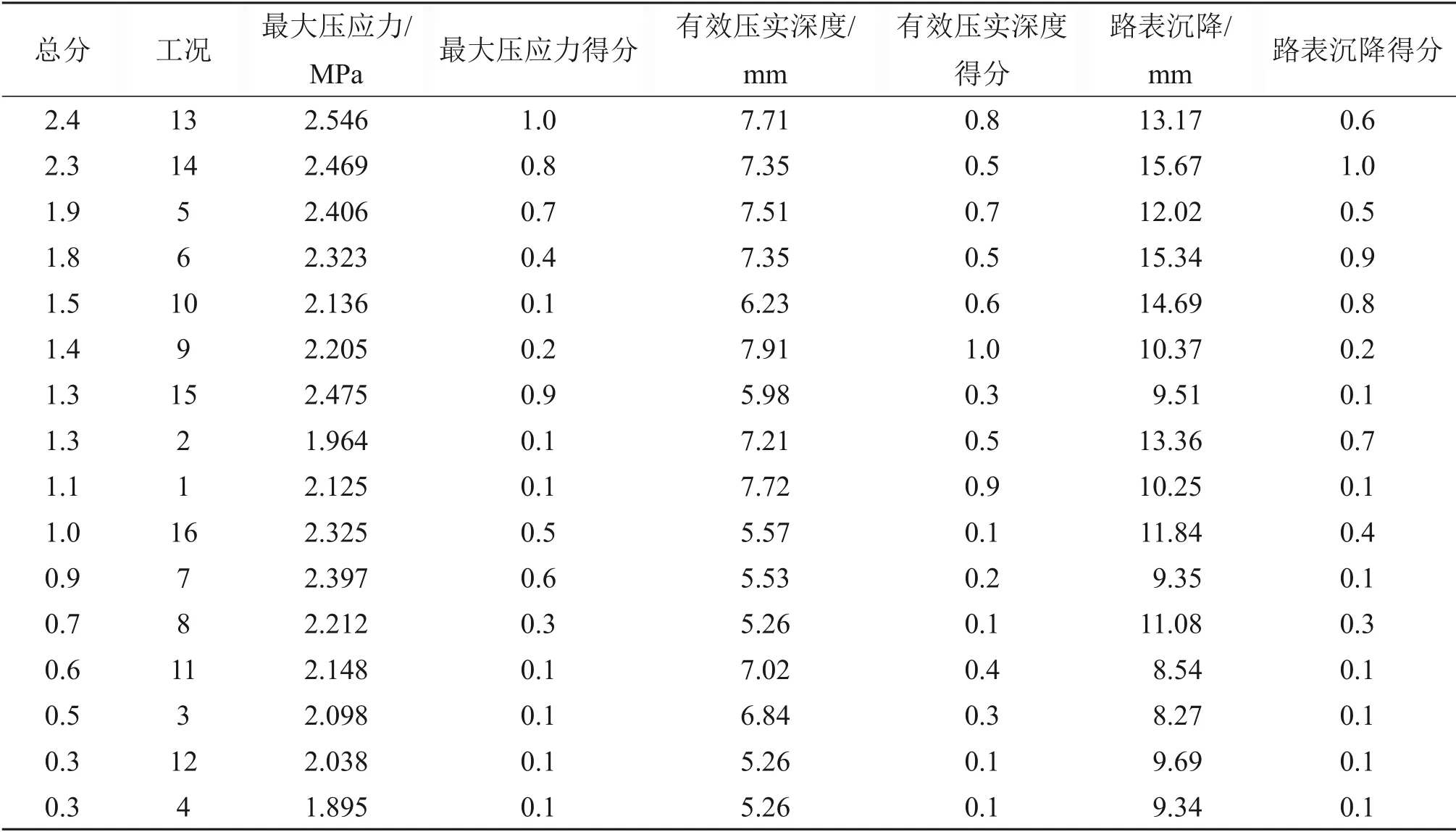
表4 各工况压实效果得分及排序Table 4 Score and sorting of compaction effect of each operating condition
分析各工况得分情况可知,增加振动轮质量可在一定程度上增大路基填料的最大压应力、有效压实深度和路表沉降,但无法高效提升填石路基的压实效果;增大振动轮激振力可有效增大路基填料的最大压应力和路表沉降,但对有效压实深度的影响较小;当振动频率由28 Hz 增大至33 Hz时,路基填料的最大压应力、有效压实深度和路表沉降均显著下降,说明28 Hz更有利于填石路堤压实;当压路机行驶速度由2 km/h 增大至4 km/h时,路基填料的最大压应力和有效压实深度略减小,这是因为行驶速度越快,振动轮的作用次数越少,但4 km/h 压路机行驶速度使路表沉降效果较好,且施工效率大幅度提升。
通过以上对比分析发现:当振动轮质量为11 t时,工况5 和工况6 得分靠前;当振动轮质量为13 t时,工况13和工况14得分靠前,这4种工况压实效果总体上较好。因此,综合考虑各种压实工况下路基最大压应力、有效压实深度、路表沉降的数值模拟计算值及排序,确定优选的压实工况组合如下:振动轮质量分别为11 t 和13 t 的2 种压路机,优选激振力为400 kN,振动频率为28 Hz;压路机行驶速度为2 km/h 和4 km/h 的压实效果总体上差别不大,且考虑到路表沉降可更直观地反映压实效果,在4 km/h 压路机行驶速度下可获得更优的路表沉降,并大幅提升施工效率,因此,压路机行驶速度推荐值为4 km/h。
3 压实工艺工程验证及效果评价
3.1 填料压实技术指标要求
在进行填石路基压实施工时,必须给石料提供克服摩擦力、黏结力和重力等阻碍其运动的能量,这就需要合理选择压路机振动工作参数。目前本领域常用的做法是先修筑100 m左右的试验路段[22-23],在试验路段反复尝试,通过测试不同碾压遍数下的压实度,最终确定合适的压实遍数。对于填石路堤来说,压实度的检测十分费时费力,要在密实的填石路基上挖一定深度的试坑,用灌水法测试压实度,测试完成后还要回填试坑、压实试坑,同时还要观测沉降差来确定压实效果。但为了与上述推荐的2种工况进行对比分析,需结合上述的2 种工况,在试验路段展开现场压实试验。
路基填筑石料采用工地碎石场生产的碎石,而碎石场的石材主要为弱风化灰岩隧道弃渣,单轴饱和抗压强度大于60 MPa(平均值约65 MPa),属于硬质岩石。根据JTG D30—2015“公路路基设计规范”[24],路堤填料粒径应不大于500 mm,并不超过层厚的2/3,不均匀系数为15~20;在路床底面以下400 mm 内,填料最大粒径不得大于150 mm,其中小于5 mm的细粒质量分数应不小于30%;路床填料宜采用砂砾、碎石等水稳性好的粗粒料,填料最大粒径应小于100 mm。本试验路段填石路基和路床的填筑采用如表5所示的填料类型和粒径。

表5 K148+510~K148+680试验段路基填筑参数Table 5 Subgrade filling parameters of test road K148+510~K148+680
3.2 现场压实方案选择
根据填石路基的工程特性,路基表面一定深度范围内的填料受到振动轮的明显冲击作用,其竖向应力明显增加,导致振动轮周围土体发生显著沉降,表明路基填料被有效压实。目前,本领域通常通过增加振动轮质量来获取预期压实效果,增加振动轮质量虽可在一定程度上增大路基填料的最大压应力、有效压实深度和路表沉降,但无法有效提高填石路基的压实效果;增大振动轮激振力可有效增大路基填料的最大压应力和路表沉降,但对有效压实深度的影响较小;而振动频率和压路机行驶速度一般凭经验设定,但由于实体工程中填石路基较少,凭经验设定也大多是参考填土路基,并未考虑实际的填料特性,且对于填石路基本身来说,填料通常是岩质隧道以及路堑边坡的爆破作业形成的,填料特性差异性很大,采用经验值设定振动频率和压路机行驶速度缺乏针对性和科学性,因此,在试验路段提出几种不同的压实方案。
填石路基压实一般采用18 t以上的重型振动压路机和激振力较大的压路机[25],保证不同粒径石料能够得到充分压实。为了使现场压实方案与推荐采用的工况5和工况13相对应,且为了体现2段试验路的不同压实效果,施工现场的压路机具体参数见表6。对本试验路段填石路基的2 个压实施工段(K148+510~K148+595 和K148+595~K148+680,长度为170 m,填方高度为5.5~7.6 m,路面宽度为33 m,双向6 车道,每个车道3.75 m)分别提出如表7和表8所示的压实方案。但考虑到施工进度,相比于2 km/h 的行驶速度,压路机行驶速度为4 km/h可以显著提高施工效率,因此,采用备选工况6 和工况14 分别在试验段K148+510~K148+595和K148+595~K148+680 进行压实作业。每层碾压完成后,采用不同方法检测压实度来分析2试验路段的压实效果,并结合有限元计算出的2种推荐工况压实效果,分析现场实测结果与数值模拟结果是否一致。

表6 压路机型号及参数Table 6 Roller model and parameters
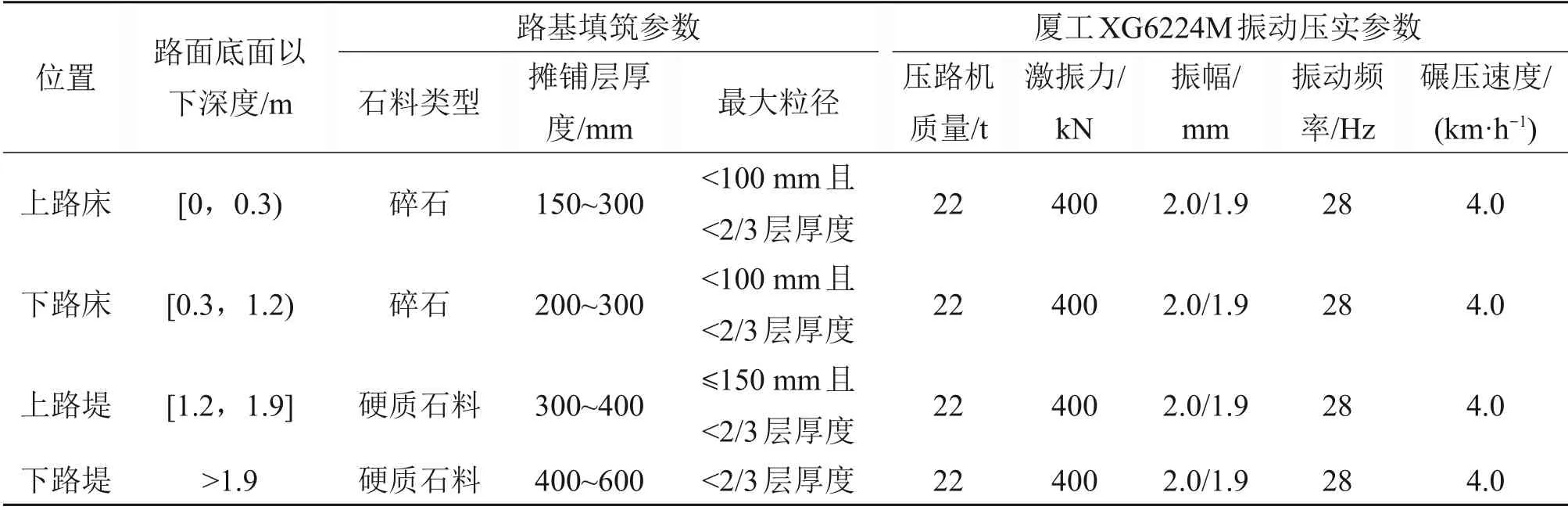
表7 试验路段K148+510~K148+595路基压实方案Table 7 Subgrade compaction plan for test section K148+510~K148+595
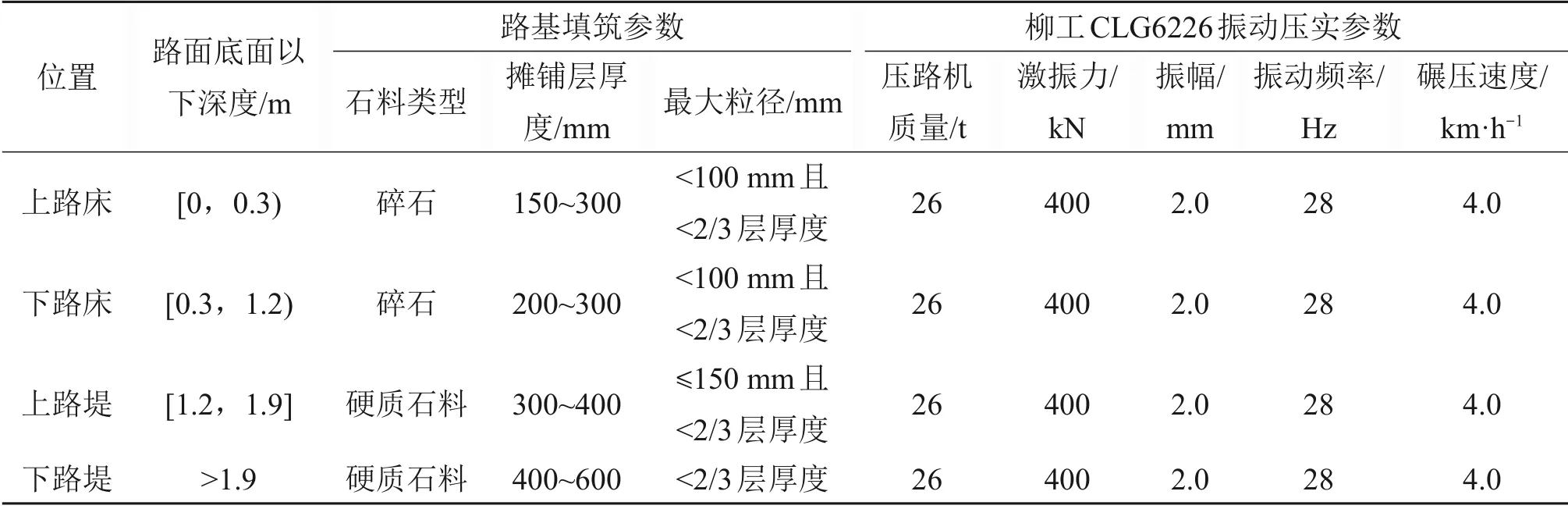
表8 试验路段K148+595~K148+680路基压实方案Table 8 Subgrade compaction plan for test section K148+595~K148+680
3.3 现场检测与数值模拟结果对比分析
压实过程拟采用初压1遍,使填料整平形成较稳定的承载层,强振5遍使不同粒径石料在激振力作用下相互咬合,形成嵌锁结构,静压2遍以消除轮迹带的压实组合形式为标准。以下路堤为例,2种试验路段下路堤摊铺厚度均为500 mm,采用2种不同型号压路机进行压实,压实完后用3种方法检测路基压实度。将水袋法测得孔隙率与数值模拟工况下有效压实深度进行对照;水准仪测得沉降差与数值模拟工况下路表沉降值进行对照;便携式落锤弯沉仪(PFWD)测得回弹模量与数值模拟工况下的最大压应力进行对照。
下路堤填料粒径比其他结构层填料粒径大,压实难度也较大,若下路堤在8 遍压实后孔隙率、沉降差满足规范要求(填石路堤压实质量控制标准如表9所示,规范要求沉降差平均值小于5 mm 且标准差小于3 mm),则说明达到预期压实效果,其他结构层的压实度均能满足要求。

表9 填石路堤压实质量控制标准Table 9 Compaction quality control standards for filling-stone subgrade
在试验路段K148+510~K148+595 和K148+595~K148+680 上每间隔17 m 左右设1 个断面,每个断面标记1个测点,每条试验路段共标记6个测点,压实后现场检测孔隙率,结果如表10所示,沉降观测结果如表11所示。
分析表10可知:孔隙率满足规范中下路堤孔隙率小于25%的要求,且采用26 t压路机试验段测的孔隙率比用22 t压路机试验段测的孔隙率小,说明该段压实有效深度较大,工况14 的压实效果比工况6的压实效果好。

表10 试验路段孔隙率现场试验结果Table 10 Results of the field test of the test road porosity %
2 段试验路的下路堤摊铺厚度均为500 mm。由表11可知:26 t压路机在碾压过程中的压实深度普遍大于22 t压路机碾压深度,压实效果较好;压路机碾压到第5 遍时所选的各测点沉降值均在2 mm以下,沉降量很小,说明当下路堤摊铺厚度为500 mm 时,碾压到第5 遍至第6 遍时沉降已基本处于稳定状态。
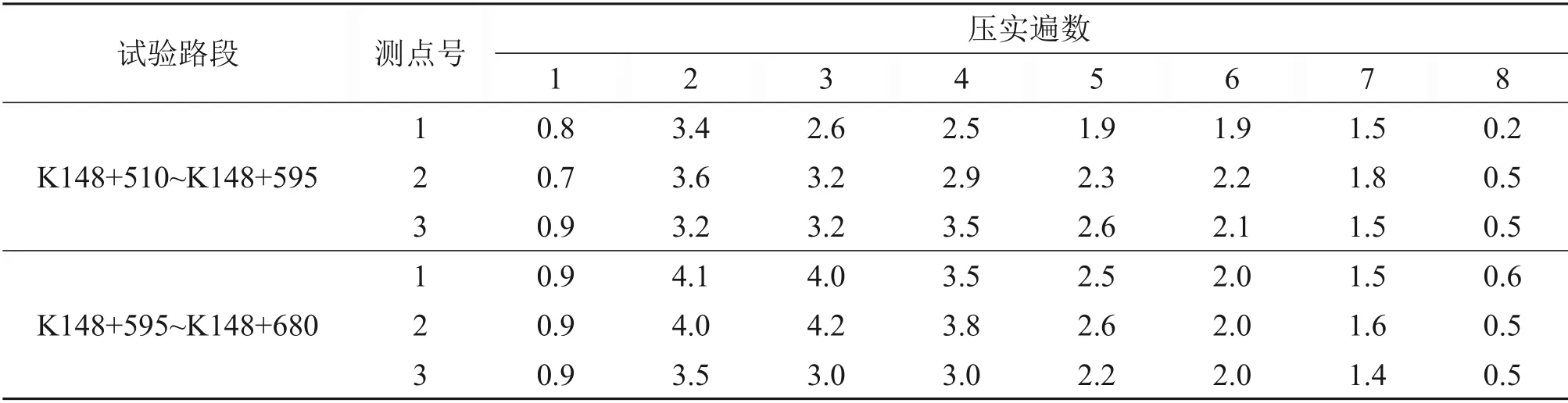
表11 试验路段沉降观测结果Table 11 Observation results of test road settlement mm
对比不同工况下的一次压实数值模拟结果可知:工况6 的最大压应力为2.134 MPa,路表沉降为12.23 mm;工况14 的最大压应力为2.222 MPa,路表沉降为12.87 mm,有效压实深度均为4.86 m。可推断试验路段K148+510~K148+595 现场压实实测结果与模拟压实工况6 结果一致,试验路段K148+595~K148+680 现场压实实测结果与模拟压实工况14 结果一致,表明提出的优选压实工艺确定方法可靠。
3.4 试验段PFWD检测与压实效果验证
考虑到填石路基的工程特性,其填料不如普通填土路基均匀,填石路基填料粒径较大,抗剪强度高,孔隙率大,因此,压实度不好控制。而上述2种压实度检测方法是较传统的方法,在试验过程中工作量大,PFWD作为一种新型快速无损检测设备,可快速检测并获取路基回弹模量[26],更科学、可靠地验证上述研究结果。
在试验路段K148+510~K148+595和K148+595~K148+680上每隔30 m设置1个断面共3个断面,在每个断面中间设置1个PFWD测点共3个测点。在22 t 和26 t(振动轮质量11 t 和13 t)这2 种压路机碾压施工后,进行PFWD 现场测试,对所得回弹模量与压实工况下路基最大压应力的数值模拟结果进行对比分析,发现这2个试验路段工后压实均能获得较大的回弹模量,压实效果好,且现场测试结果与数值模拟结果一致。压实次数与回弹模量的关系如图6所示。
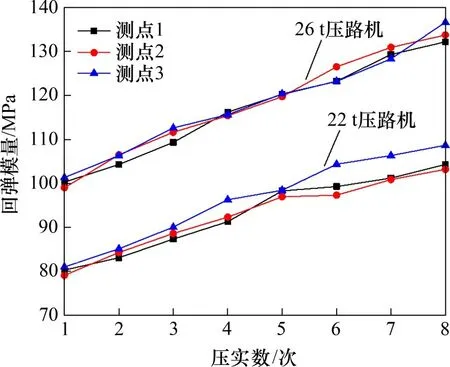
图6 回弹模量与压实遍数的关系Fig.6 Relationship between modulus of resilience and number of compaction
回弹模量越大,则路基承载能力越大[27]。试验路段K148+595~K148+680 采用的压路机质量和激振力均比试验路段K148+510~K148+595 采用的压路机的大,经检测所得回弹模量也较大,压实效果较好。PFWD检测结果进一步说明确定的优选压实工艺合理、可靠,具备推广应用价值。
3.5 基于工后沉降观测的压实效果评价
在试验路段中埋入式电感调频类智能位移计,跟踪观测填石路基的原位沉降变形,评价填石路基的压实效果,监控长期稳定性能。分别在上述2条试验路段路基顶部打孔5 m,各埋设2 个型号为JMIX-4720AT 系列电感式沉降计观测路基沉降。靠近中桩15 m、距离路肩1.5 m处分别记为沉降计1-1和2-1,距离路肩4.5 m处分别记为沉降计1-2和2-2,即经22 t压路机压实的试验路段埋设沉降计1-1 和1-2,经26 t 压路机压实的试验路段埋设沉降计2-2和2-2。沉降计布置如图7所示。
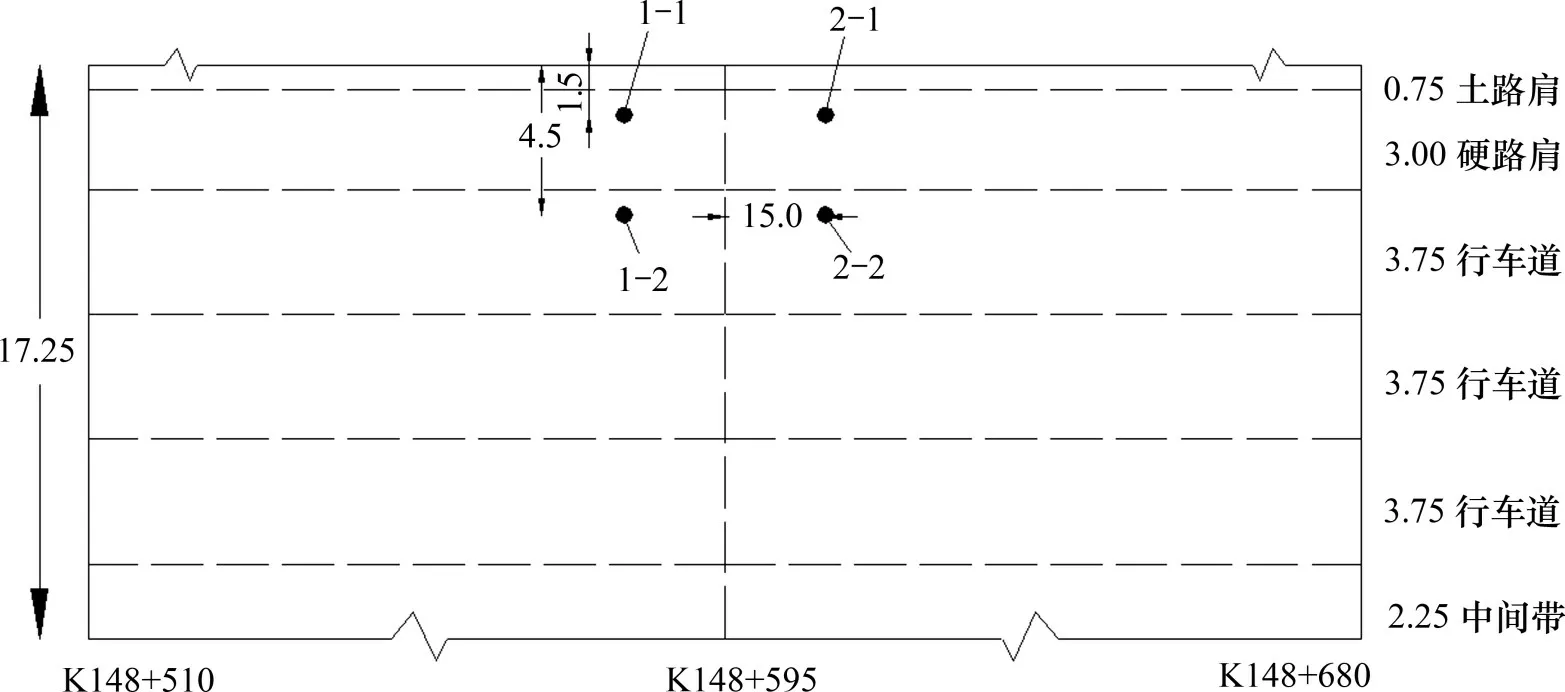
图7 沉降计布置示意图Fig.7 Schematic diagram of settlement gauge layout
监测沉降以工后首日沉降为基准,此后所得沉降均为相对沉降量,收集4 个沉降计100 d 内的沉降,所得沉降与时间的关系如图8所示。从图8可见:4 个测点在一定时间范围内都有一定沉降;K148+510~K148+595 段在100 d 内的沉降比K148+595~K148+680 段的沉降大,说明采用26 t 压路机在优选压实工况组合下碾压施工后获得了较好的压实效果。因为试验路段毗邻桥梁预制场和高架桥,是转运预制梁的枢纽,加上温湿变化,试验路段产生了一定的沉降,但沉降很小,不影响路基稳定性。
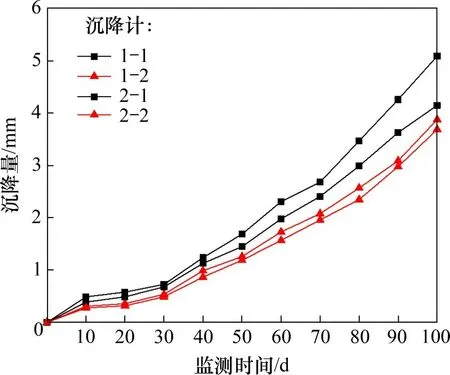
图8 沉降量与时间的关系Fig.8 Relationship between settlement and time
4 结论
1)基于弹塑性力学理论和振动压实基本原理,通过有限元软件,对振动轮质量、激振力、振动频率、行驶速度这4种参数在2种控制水平下的16种填石路基振动压实工况进行了数值模拟。
2)综合考虑各种压实工况下路基最大压应力、有效压实深度、路表沉降的数值模拟结果及排序,确定了优选的压实工况组合:振动轮质量为11 t和13 t的2种压路机,优选激振力为400 kN,振动频率为28 Hz,行驶速度为4 km/h。
3)采用22 t 和26 t(振动轮质量分别为11 t 和13 t)的压路机在优选压实工况组合下进行试验路段碾压施工,孔隙率和沉降差的检测结果均满足规范要求,压实效果好,且压实结果与数值模拟结果一致。
4)为进一步验证确定的优选压实工艺效果,采用PFWD对试验路段的回弹模量进行测试,2个试验路段均获得了较高的回弹模量;用电感式沉降计对2个试验路段进行沉降监测,PFWD测试结果与沉降监测结果均表明所提出的优选压实工艺优化方法科学可靠,实体工程压实效果好。
