南方湿热地区高液限黏土临界破坏应力室内试验与快速预估模型研究

张军辉，黄超，张安顺，李崛

(长沙理工大学公路养护技术国家工程实验室，湖南长沙，410014)

在道路与岩土工程领域，路基的塑性变形是研究人员持续关注的热点问题。对于目前常用的半刚性基层路面结构，路基的塑性变形对道路结构的稳定性至关重要[1-2]。以往研究表明，路基过大的塑性变形易导致路面发生开裂、车辙等诸多病害[3-4]。与此同时，考虑到路基运营期内的稳定性与耐久性，复杂多变的气候环境对路基变形具有潜在威胁。据气候数据显示，我国南方湘赣等地气候闷热，常年多雨，致使路基逐渐湿化，加之近年来交通量的快速增长，这些因素综合作用使得南方湿热地区路基塑性变形持续增加，其整体承载能力显著降低。目前，学者们[5-7]针对路基塑性变形行为开展研究，发现路基土在安定状态与增量破坏之间存在一个阈值，即临界应力(σcri)，当车辆循环荷载小于σcri时，路基的塑性变形能得到有效控制。显然，研究车辆循环荷载作用下路基土σcri对保障南方湿热地区的道路服役水平具有重要意义。

近年来，许多学者基于Shakedown理论建立了不同的路基土σcri取值准则，如WERKMEISTER等[8]在20世纪初发现粒状土在循环加载三轴试验过程中存在Shakedown行为，在此基础上建立了不同围压、轴差应力组合下的路基土σcri状态范围，并提出了塑性应变曲线形态法作为取值准则。GU等[9-10]基于三轴试验针对循环荷载作用下颗粒材料的塑性变形特性开展研究，得到了相似结论。考虑到当地碎石填料的特殊性，ALNEDAWI 等[11]基于不同试验条件下的三轴试验结果选取塑性变形相对曲线角度作为取值准则。QIAN 等[12]选取软质黏土进行三轴试验，发现有效循环应力比适于作为σcri取值准则。已有诸多学者对路基土σcri取值准则进行研究，但由于取土地域的差异，上述研究成果不一定适用于我国南方湿热地区路基土。

与此同时，相较于耗时费力的三轴试验，学者们认为建立一个简单、有效的σcri预估方法显得尤为必要。σcri的影响因素大致可为3类：应力变量(围压、动应力幅值等)、状态变量(相对干密度比、含水率等)以及基本物理性能指标(细粒含量、塑性指数、最大干密度等)。ZHAI 等[13-14]通过三轴试验分析不同围压条件下粗粒土、红黏土σcri的变化规律，拟合得到考虑围压的经验关系式。WANG等[15]针对不同围压、应力水平条件下青藏铁路路基冻土的动力特性开展研究，基于三轴试验结果推导出一种可较好描述应力状态影响的σcri指数预估模型。冷伍明等[16-17]进行了不同围压、动应力幅值、含水率条件下的粗粒土三轴试验，提出了可同时考虑围压、含水率的经验关系式。杨志浩等[18]对循环荷载作用下级配碎石填料的塑性应变及破坏规律进行研究，建立了综合考虑围压、细粒含量的σcri预估模型。然而，这些预估方法多适用于特定土类且影响因素选取不够全面。

为解决上述问题，本文作者以南方湿热地区常见黏土为试验土样开展基本性能试验及静、动三轴试验。首先，通过静三轴试验测定不同围压、含水率条件下土样的破坏应力；然后，通过动三轴试验分析不同围压、含水率、应力水平条件下土样在循环加载过程中的弹塑性力学行为，并结合静三轴试验结果得到相应工况下σcri；紧接着，基于三轴试验结果确定σcri取值准则；在此基础上，建立一种综合考虑应力变量、状态变量及基本物理性能指标的σcri快速预估方法，以期为路基在车辆循环荷载作用下的变形稳定分析提供有效参考。

1 试验条件及方案

1.1 依托工程简介

本研究试验用土取自莲株高速公路改扩建工程施工现场。项目起于湖南省醴陵市莲花冲，终至株洲市红旗立交桥，路段全长50 km(如图1所示)。该地区光照充足、雨量充沛，年平均气温为17.2～19.4 ℃，日照时间为1 117～1 570 h，降水量为1 278.3～2 035.8 mm，湿热现象明显，且广泛分布高液限黏土及粉质黏土等不良路基填土。

图1 莲株高速公路位置图Fig.1 Location of Lian—Zhuo expressway

近年来，随着国家环保政策的逐步完善，开山采石及占用耕地等行为被明令禁止。然而，路基填筑对土方的需求量较大，对于优质填料匮乏的地区，若调用优质土源则需付出大量的经济成本。因此，南方湿热地区的路基建设往往面临着不良路基填土不得不用的窘境。基于此，考虑到工程建设的经济性、短期性以及对通车后路基稳定及耐久性服役的迫切需求，本研究旨在提出一种路基土σcri取值准则，并建立一种快速预估方法为路基的变形分析提供有效参考。

1.2 试验土样及制备

试验土样的级配曲线及基本物理性能指标分别如图2和表1所示。根据JTG 3430—2020“公路土工试验规程”中的路基土命名准则，土样定名为高液限黏土。已有研究表明南方湿热地区公路路基含水率随着时空演化逐渐增大直至稳定在116%wOMC(wOMC为最佳含水率)左右，且含水率的变化对路基结构有着显著影响[19-20]。因此，为全面覆盖路基在湿热环境中可能的湿度状态，制备试样时含水率水平选取最佳含水率wOMC，1.1wOMC，1.2wOMC和1.3wOMC共4种工况，压实系数选取96%。考虑到三轴试验的试样尺寸要求及土样的粒径范围，试样直径选取10 cm、高度选取20 cm。此外，为尽可能避免试样在成型阶段受到扰动从而影响三轴试验结果，本研究自行研制一种对开模具用于试样制备。

表1 基本物理性能指标Table 1 Basic physical performance indicators

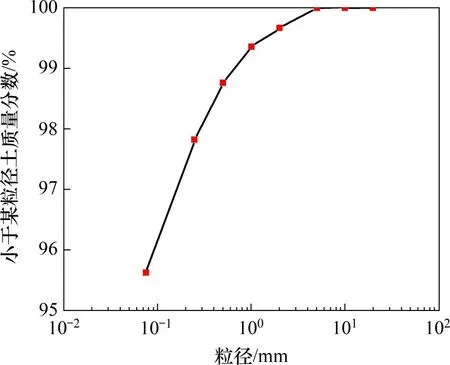
图2 高液限黏土级配曲线Fig.2 Grading curve of high liquid limit clay

试样制备流程如下：首先，对土样进行筛分，并筛余土放入烘箱进行24 h 的烘干处理；然后，进行预设含水率(最佳含水率wOMC，1.1wOMC，1.2wOMC和1.3wOMC)的土样配置，配置完成后放入密封袋中“闷料”16 h以上，以确保配置土样水分均匀分布；然后，通过式(1)得到预设压实系数(96%)所需的土质量；最后，组装对开模具，并将所需质量的土样均分为五等份依次加入模具，每加入一份便通过静压成型试验机进行压实，为防止试样在静压过程中出现分层现象，在每层静压完成后进行“拉毛”操作。试样成型后，使用保鲜膜包裹静置3 d，以确保试样水分均匀分布。

式中：K为压实系数；ρ为干密度；ρdmax为最大干密度；m为土质量；V为模具体积。

1.3 试验设备与方案

本研究选用意大利Controls 公司生产的Dynatriax100/14全自动三轴试验系统对高液限黏土进行静、动三轴试验。该系统具有较高的控制及测量精度，强大的实时数据采集功能。其三轴室通过气压控制升降，轴向载荷通过压力传感器确定，静止竖向位移可达100 mm，最大侧压力为4 MPa。

为尽可能模拟路基在运营期间的实际工况，本文参考文献[21-22]，选用12，28 和42 kPa 的围压开展高液限黏土的静、动三轴试验研究。具体工况如表2所示。试验分为2个阶段：首先，通过静三轴试验测定相应工况下试样破坏应力。其中，静三轴试验采用0.02 mm/s 的应变速率进行加载，若试样轴向应变小于15%时进入破坏状态，则取其应力峰值点作为破坏应力，若轴向应变达到15%时仍处于稳定状态，则以此时应力作为破坏应力。

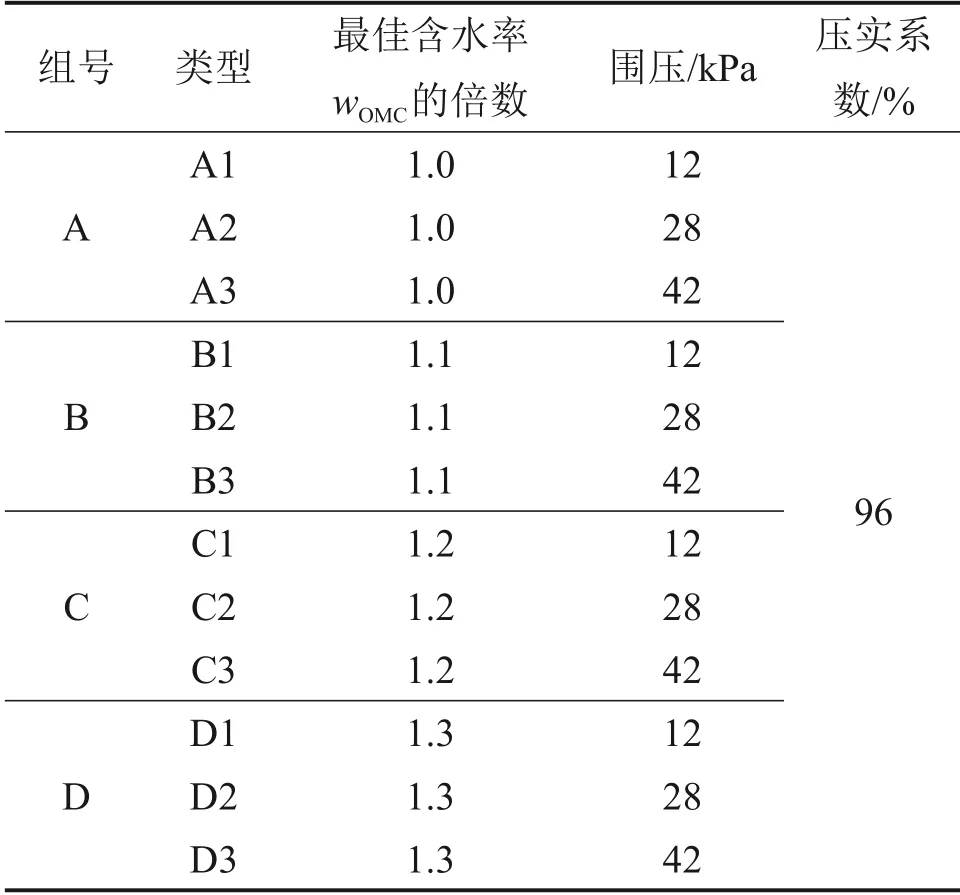
表2 静、动三轴试验工况Table 2 Static and dynamic triaxial test condition

然后，选取不同应力水平(SL，为动三轴加载应力与静三轴破坏应力之比)的循环荷载对相同工况试样进行动三轴试验，并结合静三轴试验结果获得相应工况下σcri。其中，为有效模拟车辆荷载作用影响，本文参考文献[23-24]，选取0.6SL作为起始应力水平进行动三轴加载，若起始应力水平条件下试样完成加载过程后仍处于安定状态，则增加0.1SL对另一相同工况试样再次进行加载，直至试样进入增量破坏；若起始应力水平条件下试样在加载过程中进入增量破坏，则相应减小0.1SL再次加载，直至试样处于安定状态；试样进入增量破坏时所对应应力水平可定义为临界应力水平(CSL)，进一步地，通过测定CSL获得相应工况下σcri。动三轴试验频率为1 Hz，加载时间为0.2 s，间歇时间为0.8 s，加载次数为10 000 次，考虑到试样同三轴试验系统需要一定的磨合时间，第一次加载循环的数据被剔除[25]。

2 试验结果及分析

2.1 静力作用下的破坏应力分析

为提供σcri取值依据，本文通过静三轴试验所得不同工况下高液限黏土的破坏应力如图3所示。由图3可知：随着围压的逐步增大，试样破坏应力随之提高。以表2中B1，B2和B3工况为例可知试样在12，28 和42 kPa 围压下的破坏应力分别为393，420 和454 kPa，后两者较前者分别提高了6.8%和15.5%。同样，由图3也可知试样破坏应力随含水率增大而减小。A1，B1，C1 和D1 工况试样的破坏应力分别为511，393，315 和273 kPa，后三者较前者相比分别降低了23.1%，38.4%和46.6%。可见，围压和含水率对高液限黏土的破坏应力有着较大影响。

图3 不同围压、含水率条件下破坏应力Fig.3 Failure stress under different moisture contents and confining pressures

2.2 动力作用下的弹塑性力学行为及临界应力

动三轴试验中不同工况下高液限黏土的塑性应变与弹性应变结果如图4～7所示。由图4～7中的曲线1，3 和5 可知：当试样处于安定状态时，其塑性、弹性应变随着加载次数累积表现出明显规律性：试样塑性应变随着加载次数的不断累积逐渐增加并趋于稳定，即加载初期(2 000 次加载前)塑性应变速率较大，应变增加明显，当2 000次加载后，试样塑性应变速率随之减缓，塑性应变开始趋于稳定。同时，尽管试样在循环荷载作用下经历了塑性变形累积，但该工况下的土体内部结构仍足以承受应力加载，其弹性应变随着加载次数累积逐渐平缓。

同样，由图4～7中的曲线2，4和6可知，当试样所受加载应力超出自身承受极限而进入增量破坏时，存在2种情况：一是塑性应变在加载初期快速增大，即使在4 000次加载后，塑性应变速率仍无减小趋势，弹性应变随着加载次数累积一直呈增加趋势(如图7中曲线4 所示)。二是塑性应变在加载过程中的某一节点急剧增大，弹性应变呈不稳定变化(如图6中曲线2 所示)。这是由于该工况下试样抵抗永久变形的主要阻力小于所受加载应力，其内部颗粒滑移量在加载应力的作用下逐步或迅速增加，反映在宏观表现即为试样在应力加载过程中逐步或快速进入增量破坏阶段。

图4 试样在wOMC条件下的塑性应变和弹性应变曲线Fig.4 Plastic strain and elastic strain curves of samples under wOMC

图5 试样在1.1wOMC条件下的塑性应变和弹性应变曲线Fig.5 Plastic strain and elastic strain curves of samples under 1.1wOMC

图6 试样在1.2wOMC条件下的塑性应变和弹性应变曲线Fig.6 Plastic strain and elastic strain curve of samples under 1.2wOMC

图7 试样在1.3wOMC条件下的塑性应变和弹性应变曲线Fig.7 Plastic strain and elastic strain curve of samples under 1.3wOMC

临界应力水平(CSL)即试样进入增量破坏时对应的应力水平，由上述分析可知高液限黏土在不同工况下的CSL结果(如表3所示)。结合图3和表3换算可得相应工况下的σcri，结果如图8所示。由图8可知：试样σcri随着围压增大基本呈线性增大。试验工况B1，B2 和B3 所对应的σcri分别为236，253和273 kPa，后两者较前者分别提高了7.2%和15.6%。这是因为围压增大使得土粒间的相互约束更为紧密，从而提高试样抵抗加载应力的能力。此外，由于含水率的增大使得土粒间自由水随之增多，土粒间的黏结力和摩擦力随之减小，使得当含水率从wOMC(A2 组)增加至1.1wOMC(B2 组)，1.2wOMC(C2 组)和1.2wOMC(D2 组)时，试样σcri分别从265 kPa 下降至253，201 和121 kPa，后三者较前者相比分别下降了4.5%，24.2%和54.3%。由此可见，试样σcri随围压和含水率变化而变化，其中含水率影响相较于围压更为显著。因此，控制路基土含水率对于提高路基结构稳定性十分重要。

表3 不同含水率和围压条件下CSL结果Table 3 Results of critical stress level under different moisture content and confining pressure

图8 不同围压和含水率条件下σcri结果Fig.8 Results of σcri under different moisture contents and confining pressures

2.3 临界破坏应力取值准则确定

如2.2节所述，当试样处于安定状态时其塑性应变主要发生在加载初期，随着加载次数的增加试样基本表现为弹性变形，且弹性应变逐渐趋于定值，这表明此时的弹性应变速率应当为0或接近于0。当试样进入增量破坏时，其弹性应变表现为持续增加或不规律变化，这表明此时的弹性应变速率应当大于0或呈不规律变化。因此，本文基于Shakedown理论尝试选用弹性应变速率变化作为试样σcri的取值准则。弹性应变速率计算公式为

式中：εs为弹性应变速率(正值表示弹性应变增大，负值减小)；εr(N)为第N次回弹值；εr(N-i)为第N-i次回弹值；i一般取值不小于500。

不同围压、含水率和应力水平条件下弹性应变速率曲线如图9所示，其中B2(SL=0.7)、C3(SL=0.7)、D3(SL=0.5)工况下的试样因破坏较快而未进行弹性应变速率计算。由图9可知：在多数情况下，试样弹性应变速率前期波动较大。这是因为试样在加载前期仍处于压实阶段，其内部结构呈无规律变化且弹性变形量较小，从而使得试样弹性应变速率前期波动较大。由图9(a)、9(c)和9(d)中曲线1，3和5及图9(b)中曲线1，3和4可知，当试样处于安定状态时，弹性应变速率随着加载次数累积逐渐向0 靠近且最终稳定在-0.3×10-2～0.3×10-2区间内波动。这是因为试样在经历加载前期的压实阶段后，其内部结构足以承受此时的加载应力，从而使得试样随着加载次数的增加而进一步密实，最终弹性应变速率表现为0 或接近于0。同样，由图9(a)中曲线2，4和6可知，当试样进入增量破坏时，其最终弹性应变速率分别稳定在0.52×10-2，0.68×10-2和1.16×10-2，其他破坏状态下的试样有着类似变化趋势。值得注意的是，图9(c)中曲线2 的弹性应变速率在6 000 次加载后直接进入负值。这是因为试样在经历加载前期的压实阶段后，其内部结构不足以承受此时的加载应力，从而使得试样随着加载次数的增加逐步或迅速地进入增量破坏状态，最终弹性应变速率表现为稳定在某一正值或急剧减小且最终无定值。

图9 不同围压、含水率和应力水平条件下弹性应变速率曲线Fig.9 Elastic strain rate curve under different confining pressures,moisture contents and stress levels

综上所述，当试样处于安定状态时，最终弹性应变速率稳定为0 或接近0。而当试样进入增量破坏时，弹性应变速率存在2种情况：一为试样逐渐破坏时，最终弹性应变速率稳定为某一正值；二为试样迅速破坏时，弹性应变速率急剧减小且最终无定值。因此，本文基于Shakedown理论选取单次循环荷载周期下-0.3×10-2～0.3×10-2范围的最终弹性应变速率为高液限黏土σcri的取值准则。

3 临界破坏应力预估模型

3.1 模型构建及适用性分析

综上所述，本文在前人研究[13-17]及本文高液限黏土三轴试验结果基础上建立一个综合考虑应力变量(围压)、状态变量(含水率、相对干密度比)、基本物理性能指标(塑性指数权)的σcri预估模型，如下式所示：

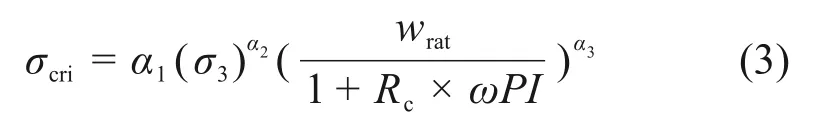
式中：σcri为临界破坏应力；σ3为围压；wrat为实际含水率与最佳含水率的比值；Rc为相对干密度比；ωPI为塑性指数权，为IP与P0.075的乘积；α1，α2和α3为模型参数。

为验证本文所建立模型的准确性与适用性，除本文数据外，收集文献[24,26-28]中路基土的基本物理性能指标(见表4)及σcri试验数据对新模型进行拟合，结果如表5所示。由表5可知：新模型较好地耦合了不同路基土的试验数据，且相关系数为0.83～0.98，具有较高的预估精度。因此，新模型具有较高的准确性与适用性，可推广应用于其他路基土，以及相同路基土在其他工况下的σcri预估。

表4 不同路基土的基本物理性能指标对比Table 4 Comparison of basic physical performance indexes of different subgrade soils

表5 不同路基土的拟合参数对比Table 5 Comparison of fitting parameters of different subgrade soils

3.2 模型参数回归分析

为快速、准确地获取路基土σcri预估模型参数，本文选用SAS 统计分析软件对路基土基本物理性能指标进行统计分析，从而对本文所建立模型的模型参数进行预估。首先，根据表4选取不同路基土的液限ωL、塑限ωP、塑性指数IP、细粒质量分数P0.075和最大干密度ρdmax作为基本物理性能指标变量，并建立组合变量DmaxP和DmaxIP来反映基本物理性能指标的综合影响，如式(4)和(5)所示[29]。然后，对上述变量进行逐步回归分析，确定影响σcri模型参数的重要变量，并将其与模型参数(α1，α2和α3)建立系数较高的经验关系式，如式(6)所示。在此基础上，可通过路基土基本物理性能指标结合式(6)得到模型参数α1，α2和α3，紧接着在给定围压、含水率、相对干密度比、塑性指数权条件下通过式(3)对路基土σcri进行预估。

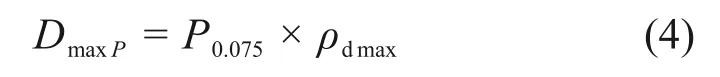
4 结论

1)由静三轴试验结果可知，在其他条件一定的情况下高液限黏土破坏应力随围压的增大而增大，随含水率的增大而减小。由动三轴试验结果可知，当试样处于安定状态时其弹性、塑性应变随着加载过程的进行逐渐趋于定值。当试样进入增量破坏时存在2种情况：一是其弹性、塑性应变随加载次数累积一直呈增加趋势；二是塑性应变在加载过程中急剧增大达到峰点值，弹性应变呈不稳定变化。

2)结合静、动三轴试验结果确定不同围压和含水率条件下的高液限黏土σcri，发现在其他条件一定的情况下σcri随围压增大基本线性增大，随含水率增大呈基本线性减小，且含水率影响相较于围压更为显著，说明控制路基土含水率对于提高路基结构稳定性十分重要。

3)基于三轴试验结果可知，当试样处于安定状态时，其最终弹性应变速率稳定为0 或接近0。当试样进入增量破坏时，其弹性应变速率存在2种情况：一为试样逐渐破坏，最终弹性应变速率稳定为某一正值；二为试样迅速破坏，弹性应变速率急剧减小且最终无定值。在此基础上，选取单次循环荷载周期下-0.3×10-2～0.3×10-2范围的最终弹性应变速率作为高液限黏土σcri取值准则。

4)提出综合考虑应力变量(围压)、状态变量(含水率、相对干密度比)、基本物理性能指标(塑性指数权)的路基土σcri预估模型，且通过本研究及已有文献试验数据验证了所提模型的准确性和适用性。此外，建立模型参数与基本物理性能指标间的经验关系式从而在试验条件受限情况下对σcri进行快速预估。

5)为保证路基在运营期间的稳定性及耐久性，在进行道路设计时应考虑路基所受荷载不得超出相应工况条件下的σcri，即以σcri作为路基所受荷载的最大控制上限。