球型调节阀关阀水锤效应的试验研究与数值计算
2021-10-25陈亚飞顾卫国王德忠许锐
陈亚飞,顾卫国,王德忠,许锐
(上海交通大学机械与动力工程学院,上海 200240)
核电站中,常发生关阀水锤现象,威胁设备安全.1978年底,美国NRC把水锤问题列为“尚未解决的安全问题,A-1”[1].为了防止流体介质泄漏超标,常常需要快速关闭阀门.而在阀门快速关闭的瞬态过程中,流体的动能急剧向压力势能转换,导致局部压力急剧变化,在管路中会产生一系列急骤的压力交替变化现象,出现严重的水锤现象,威胁设备安全.
对水锤现象的系统研究始于19世纪末,俄国JOUKOWSKY推导出经典的水锤动量方程[2].WYLIE等[3]提出水锤计算的数值方法,并总结一系列水锤防护措施,带动了水锤数值计算的热潮.但传统的水锤计算方法将逆流发生时阀门关闭情况简化为瞬时,与实际情况有所差异,如马光飞等[4]基于FLUENT软件分析了球阀的水力性能.为了研究阀门关闭的动态特性,邹亮等[5]、赵云等[6]利用动网格方法模拟球型单向阀关闭的过程.计算流体力学(CFD)方法虽然可以得到丰富的流场信息,但适用性较差,处理非轴对称结构的复杂模型尤为困难.由于动网格技术的限制,通常需要将实体模型简化为二维平面模型才能保证计算收敛.对于阀门与管路系统内的流体介质瞬态流动,更是难以采用商业CFD计算软件进行计算.实际上,当管路系统中产生剧烈压力波动时,流体压力的轴向变化远大于径向变化.因此,适宜忽略径向流动差异,将实际水锤现象近似为一维流动进行计算.特征线法(MOC)是计算水锤现象的常用方法,广泛应用于复杂管路和复杂边界条件下.左巧林等[7]基于特征线法开发水锤计算程序,模拟了压水堆核电站一回路中泵和止回阀系统切换工况时的单相水锤特性.薛宏林等[8]采用MOC法模拟停泵过程,并对比了试验数据.王思琪等[9]使用数值方法对空气罐进行水锤防护分析.YANG等[10]提出使用耦合MOC与CFD的停泵水锤数值计算方法.
除了数值计算的研究,试验方法也是研究水锤现象不可或缺的一环.刘汉勋[11]采用试验方法测量出2种压水堆用新型止回阀在冷却剂倒流情况下的水锤波形,并得到水锤冲击压力与水流速的关系图.RAHMEYER[12]提出一种可以动态测量止回阀突然关闭的试验装置,并讨论了阀门与管道特性对压力波动的影响.杨帅[13]搭建了一套可以测量关阀水锤效应的试验装置,但只测量了0.02 s关阀时间下的水锤现象,而没有分析较长关阀时间(如超过1 s)下的水锤效应试验.张鹤等[14]采用数值计算和试验方法研究了单向球阀瞬态开启时的阀门压降.
目前缓开阀门的关阀水锤研究还比较缺乏试验验证.因此,文中旨在通过搭建储罐-管道-阀门(reservoir-pipeline-valve, RPV)试验系统,研究一定关阀时间下的关阀水锤效应规律,分析关阀速度对水锤冲击波形的影响.同时基于水锤方程和特征线法,开发计算软件,建立一套快速分析关阀瞬态性能和水锤冲击现象的数值计算方法.
1 研究对象
球型调节阀结构精简,便于操作,广泛应用于城市给排水、石油化工、核电等领域.文中研究对象是一种口径为25 mm的不锈钢球型调节阀,工作环境为常温常压.
为研究关阀水锤现象,搭建RPV试验系统,如图 1所示.试验系统包括高位水箱、低位水箱、输水管道、待测阀门、压力表、控制阀等.高位水箱置于3 m高的试验台架,水量蓄满.低位水箱置于水平地面,水面满溢.利用重力势能输运流体,当高位水箱的体积足够大时,可认为阀门进出口压力保持恒定.阀前水平管长为8 m,阀后管长为4 m.管道内径25 mm,管道壁厚4 mm.使用美国OMEGA公司的高精度压阻式压力传感器测量阀前、阀后压力脉动,采用压差传感器测量阀芯压降.压力传感器量程为345 kPa,压差传感器为103 kPa,精度(综合线性度、滞后性和重复性)为0.08%,响应时间小于1 ms,耐受压力为300%量程.为保证单相流条件,采用控制阀和电磁流量计调节管路流量.电磁流量计的量程为10 m3/h,精度为0.5%.使用角位移传感器测量待测球阀的开度.传感器的独立线性公差为0.1%,电器转角345°.通过NI USB-6221型数据采集仪,基于Labview2015开发数据采集程序,能够实时获得压力、流量、开度等多个通道信号的振幅和频率.

图1 RPV试验系统
试验过程中,首先关闭所有阀门,将高位水箱和低位水箱蓄满合适水量.再打开控制阀与待测球阀,调节控制阀至预定工况.待管路水力参数稳定后,手动关闭待测球阀,引起关阀水锤效应,测量阀门前后压力、流量等参数直至水锤现象结束.
2 数值计算方法
2.1 特征线法
将流体视为可压缩介质,忽略管路截面上的流动差异.基于一维水锤方程和特征线法,建立描述阀门动态特性及管道水锤效应的数值计算模型.
由于流体宏观运动的速度远小于压力波在水中的传播速度,忽略影响较小的流速项,并假设管道水平,管道直径沿长度不变,则流体的动量方程和连续性方程为
(1)
(2)
式中:g为当地重力加速度;H为压力水头;v为流体速度,以向右为正;x为轴向距离;t为时间;λf为流阻系数;a为水锤波传播速度,与管壁材质、尺寸、支撑方式以及流体介质弹性模量等参数均有关系[15],
其中,K为流体介质的体积弹性模量;ρ为流体介质的密度;D为管道直径;E为管壁材料弹性模量;δ为管壁厚度;c为管道的支撑系数,若管道固定无轴向运动,取0.91.
引入特征值λ=±g/a,可将式(1),(2)化为2组常微分方程:
(3)
(4)
由上式可见,管道中流体压力以波的形式传播,其传播速度为a.由于传播速度a有正负,管道中的压力就等于这2个方向水锤波的叠加.此时管道中的压力分布不仅与时间有关,而且与位置有关.将管道在x方向离散成N等份,每等份的长度Δx,将时间步长取为Δt.如果Δt=Δx/a,则网格的对角线斜率为+1/a或-1/a,分别满足式(3)和式(4)的第2个方程.将速度v用流量Q代替,沿特征线对式(3),(4)第1个方程进行差分.由当前时刻节点i-1处的压力Hi-1、流量Qi-1和节点i+1处的压力Hi+1、流量Qi+1,迭代求出下一时刻节点i处的压力Hi和流量Qi
(5)
(6)
(7)
式中:A为管道截面积;B和R为计算的常数;CPi,CMi为计算的过程量.
2.2 边界条件
由于阀门流阻系数与管道流阻系数不同,需要联立阀门前后节点的特征线方程、流体连续性方程与阀门自身的流阻特性方程进行求解.由阀前节点up和阀后节点down的压力和流量,求得阀前节点up+1与阀后节点up+2的压力和流量,如图2所示.

图2 阀门前后节点示意图
Hup+1=Hup-B(Qup+1-Qup)-RQup|Qup|,
(8)
Hup+2=Hdown+B(Qup+2-Qdown)+RQdown|Qdown|,
(9)
Qup+1=Qup+2,
(10)
(11)
阀门流阻特性方程通过试验测得.为避免人为因素和测量仪器的随机误差,进行了重复性试验,阀门的流量和压降选取2次测量值的平均值,并采用指数多项式拟合阀门的流阻特性曲线.
3 结果与讨论
3.1 关阀水锤试验
通过快速关闭待测球阀诱发RPV试验系统的水锤现象,关阀速度尽量保持为匀速.当关阀时间tc取3 s时,测得球阀的阀前压力pu、阀后压力pd以及水锤冲击合力pt随时间t的变化曲线,如图3所示.
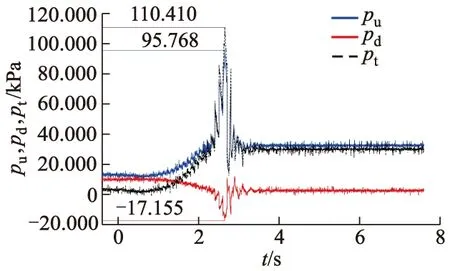
图3 阀前、阀后压力变化曲线(3 s关阀)
由图3可以看到,由于待测球阀的流阻系数很小,初始时刻的阀前、阀后压力近乎相等.当阀门逐渐关闭时,阀前压力逐渐升高,并在2.748 s达到最大值95.768 kPa.随后,阀前压力逐渐降低,并伴随出现一定强度的随时间推移迅速衰减的压力波动.与阀前压力的变化趋势相反,阀后压力先是随着阀门关闭而降低,并在2.756 s达到最小值-17.155 kPa,大于常温清水的饱和蒸汽压-99.263 kPa,所以试验过程中没有发生空化现象,只发生单相流水锤现象.此后,阀后压力经历数次大幅度的波动,并在2.995 s达到最大值11.853 kPa,甚至超过了初始时刻的阀后压力.但阀后的压力波动最终也随时间迅速衰减.不难发现,阀前压力和阀后压力几乎同时达到峰值和谷值,说明管道中流体压力以波的形式传播,验证了水锤方程的双曲型方程性质,为使用特征线法进行数值计算提供了有力支持.同时,阀前的正压力与阀后的负压力也会产生合力,对阀体结构造成更大的水锤冲击力,合力的最大幅值约为110 kPa.水锤冲击力在阀前的最大振幅约75 kPa,而在阀后的最大振幅约25 kPa,说明关阀水锤效应对阀前管路的冲击力更强.
此外,图 3也表明了在关阀水锤试验中,阀门关闭后的管道压力脉动幅值随时间衰减明显.其可能的原因是管道支撑形式的刚性较低,压力波传递时不会出现明显的周期性衰减,从而导致管道中的压力脉动迅速衰减.
3.2 关阀时间对水锤冲击波形的影响
基于RPV试验系统的关阀水锤试验,设置3 s关阀、5 s关阀2组试验工况,对比分析关阀时间对水锤冲击力的影响.试验结果如图4所示.

图4 不同关阀时间的影响
试验结果表明,2种工况下阀前压力、阀后压力的变化趋势基本一致.随着阀门关闭,阀前压力先增加后降低,阀后压力先降低后增加,并都伴随出现一定强度的随时间推移快速衰减的压力波动.因为阀前压力变化的主峰值明显高于正常流动时的压力值,并且峰值出现在阀门完全关闭之前,所以可判断发生的水锤现象为间接水锤.对比3 s关阀和5 s关阀2组试验工况可以发现,后者的阀前压力峰值略有降低,而阀后压力谷值基本不变.所以,增加关阀时间,可以在一定程度上降低水锤冲击力的幅值.这与文献[16-17]中相应的结论基本一致.为了更好地保护阀门,不仅要增加关阀时间,还需要合理设计关阀速度,尤其是在阀门即将关闭的瞬间,要尽量降低关阀速度.此外,由图 4可以看到,2种工况下的水锤冲击波形不同.3 s关阀的压力脉动波形为单峰,而5 s关阀的压力脉动波形为双峰.这可能是因为当关阀速度减小时,流量减小的速度更慢,水锤的反向冲击波会叠加到初始冲击波上,产生多个峰,同时也会降低压力幅值.
3.3 试验与数值计算对比
根据3 s关阀水锤试验,采用自主开发的计算软件进行数值计算.数值计算与试验的研究对象一致.管道材料取不锈钢,密度7 900 kg/m3,弹性模量194 GPa.流体介质为20 ℃清水,忽略水中微小气泡对流体体积模量的影响,体积模量2.18 GPa.水锤波速a为1 432.9 m/s.试验初始时刻的阀门开度OD为100%,管路流量为3.96 m3/h.管道末端的绝对压力为101.325 kPa,管道始端的绝对压力为131.723 kPa.在数值计算中,采用三角函数OD=OD(t) 拟合试验测得的阀门开度,如图 5所示.

图5 开度变化曲线
对比试验值与计算值的阀前、阀后压力变化曲线,如图 6所示.可以看到,试验方法与数值计算得到的水锤冲击波形基本一致.阀前压力的试验值pu,exp在2.748 s达到最大值95.770 kPa,计算值pu,com在2.692 s达到最大值71.500 kPa.试验值与计算值的时间偏差约为2%,峰值误差约为12%.阀后压力的试验值pd,exp在2.756 s达到最小值-15.678 kPa,计算值pd,com在2.691 s达到最小值-11.297 kPa.二者的时间偏差约为2%,谷值误差约为5%.因此,计算软件能够较为准确地预测阀门前后的压力变化趋势,但计算得到的阀前压力峰值比试验值约低12%.说明特征线法计算得到的水锤冲击力偏小,所以在实际应用中要考虑采用更大的材料安全系数,以防设备因水锤冲击而损坏.造成误差的原因可能是未考虑溶解氧、微小气泡等对流体物性的影响,也可能是拟合的阀门流量特性曲线对低开度下流阻系数的描述不够准确.另外,由于角位移传感器响应时间的影响,当关阀速度较快时,关阀时序信号准确性不足,也会导致计算结果与试验结果的误差增大.考虑到仪器测量误差、球阀加工精度、数值计算模型的简化等影响,综合调研相关文献,可以认为二者吻合较好.因此,通过试验验证,计算软件对关阀瞬态过程和管道水锤效应的预测是可信的.文中的数值计算方法可以支撑相关的工程应用.

图6 对比软件计算值与水锤试验值的压力变化曲线
4 总 结
1) 试验测量3 s关阀的水锤效应,发现随着阀门关闭,阀前压力先增加后降低,阀后压力先降低后增加,二者几乎同时达到峰值和谷值,并都伴随有一定强度的随时间推移快速衰减的压力波动.关阀水锤效应对阀前管路的冲击更强,并且阀前正压力与阀后负压力会产生合力,对阀体结构造成更大的水锤冲击力.
2) 将关阀时间从3 s增加到5 s,阀前压力峰值降低14 kPa,而阀后压力谷值增大3 kPa,所以水锤冲击力约降低17 kPa. 2种工况下的阀前、阀后压力变化趋势基本一致.
3) 基于经典水锤方程和特征线法,自主开发计算软件,建立一套快速分析关阀瞬态性能和水锤冲击效应的数值计算方法.通过与关阀水锤试验结果的对比,验证了计算软件的可靠性.计算软件能够较好地预测关阀瞬态过程和管道水锤效应,为相关工程应用提供技术支撑.
