一类带有未知时延的随机系统自适应控制
2021-10-25汝浩男赵前进
汝浩男,赵前进,吴 健,3
(1.安徽理工大学计算机科学与工程学院,安徽 淮南 232001;2.安徽理工大学数学与大数据学院,安徽 淮南 232001;3.安庆师范大学计算机与信息学院,安徽 安庆 246000)
目前常见的动力系统数学模型主要是非线性系统模型,在非线性系统的自适应控制器设计中,反步法(Backstepping)是一种广泛使用的方法。但是在应用该方法时随着系统阶数的增长, 计算量也大幅增长。 为了解决这一问题, 文献[3]提出了动态面法(dynamic surface control,DSC)以大幅降低计算量,目前该方法已广泛使用;文献[4]展示了该方法在一个无人艇航向控制中的应用;文献[5-6]将该技术扩展至随机非线性系统的反步设计过程,提出了多种动态面控制器设计方法。在许多非线性系统中,系统方程含有未知函数,因此利用神经网络来逼近未知函数是很重要的一步。文献[7]研究了在实际的非线性系统中如何使用神经网络来逼近未知的函数。文献[8]在一类多输入多输出非线性系统中利用神经网络跟踪未知函数,解决了在含有时间延迟和外部扰动的情况下的自适应控制问题。文献[9]利用神经网络研究了非线性系统的鲁棒H
跟踪控制问题。随机干扰是许多非线性系统中无法避免的,它们常使系统状态变得不稳定,因此解决系统中的干扰问题是很重要的。文献[12]通过进行非线性映射,将状态约束系统转化为相同控制目标的无约束系统,解决了一类含有状态约束的非线性随机系统的自适应控制问题。时延现象在工程应用中也是十分常见的,它常常对系统的稳定性造成影响,因此对于时延现象的研究引起了广泛的重视。文献[14]完成了在含有输入饱和特性的非线性时延系统中构建控制器的工作,解决了一类特殊非线性系统的有限时间控制问题。而含有状态约束和未知时延的非线性随机系统的有界稳定问题也得到了广泛的关注。
目前,非线性系统模型已引起广泛关注,在工业生产中,许多物理过程均可抽象为此模型,利用此模型可研究动力系统的运行过程。如文献[16]中介绍了该模型在电力系统控制方面的实际应用,并利用此模型处理电力系统的信号切换问题。但是在工业生产环境中,许多实际系统包含未知时延和随机扰动。它们常使系统状态变得不稳定,对控制器的设计造成困难。
在不含时间延迟和随机扰动的情况下,已有实用的控制策略能实现该系统的有界稳定控制目标。但是当加入输入时延时,现有控制器无法得到理想的结果,而当系统加入随机扰动时,现有的控制策略就会失效。本文提出一种基于反步法的动态面控制技术,并构造控制器以实现系统依概率有界稳定的跟踪控制目标。为了解决系统中存在不确定函数的问题,使用神经网络来逼近未知函数,并利用动态面方法处理“复杂性爆炸”的问题。为了处理输入时延,本文引入一个补偿系统,并用一类Lyapunov-Krasovskii函数来补偿未知的状态时延函数。最后通过仿真实验验证所提出控制方法的有效性。
1 问题描述和预备知识
1.1 系统描述
考虑一类含有未知状态时延和输入时延的非线性随机系统

(1)

y
(t
),设计一个自适应神经网络动态面控制器使得该闭环系统的所有信号都半全局依概率有界和跟踪误差y
-y
依概率有界。
1.2 预备知识
对于如下形式的随机系统
dx
=φ
(x
)dt
+ψ
(x
)dw
,x
∈R
(2)
式中:x
表示系统状态,φ
(x
)∶R
→R
和ψ
(x
)∶R
→R
×是局部Lipschitz函数,w
是k
维标准Wiener过程。定义1对于任意给定的Lyapunov函数V
(x
)∈C
,微分算子L
定义如下
(3)
式中:Tr
(·)表示矩阵的迹。引理1对于随机系统(2),存在一个C
函数V
(x
)∶R
→R
,使得下面不等式成立
(4)

E
[V
(x
)]≤V
(x
)e
-+o
/o
,∀t
≥0
(5)
引理2对于a
≥0(i
=1,2,...
,n
,q
>1) ,有以下不等式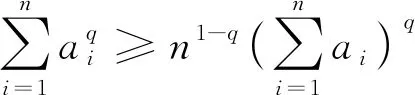
(6)
对于在紧集Ω⊂R
上的任意未知连续非线性函数F
(Z
),存在神经网络W
*S
(Z
)使得F
(Z
)=W
*S
(Z
)+δ
(Z
),∀Z
∈Ω⊂R
,其中S
(Z
)=(s
(Z
),…,s
(Z
))∈R
是向量函数,l
>1是神经网络节点数,s
(Z
)定义如下
μ
=[μ
1,…,μ
]是s
(Z
)的中心,η
为高斯函数宽度,W
是理想权重向量,其值定义如下
2 自适应神经网络跟踪控制
2.1 控制器设计

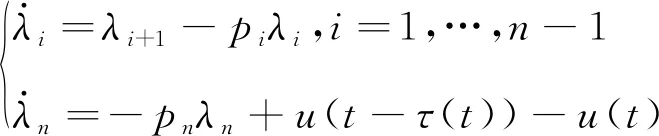
(7)
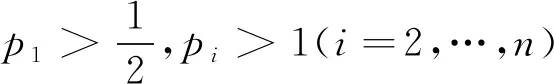

(8)
其中:ϑ=y
,ϑ(i
=2,…,n
)是一阶滤波器输出。使虚拟控制器α
-1通过一阶滤波器,滤波变量ϑ设计如下
(9)
其中:v
是滤波器时间常量。第1步:根据系统(1)和子系统(7)有
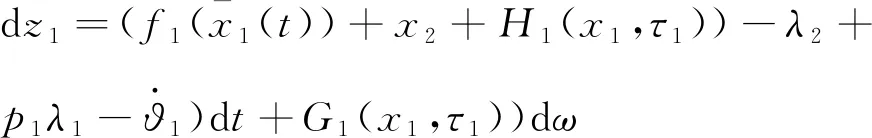
(10)
定义如下的Lyapunov函数

(11)



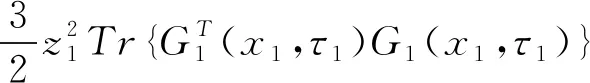
(12)
其中:e
=ϑ-α
。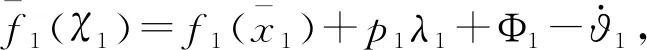

利用神经网络逼近未知函数可得

(13)


(14)
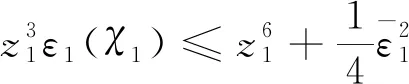
(15)

(16)
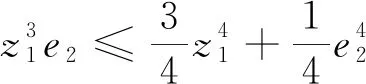
(17)

(18)

(19)


(20)

(21)
根据公式(13)~(19),公式(12)可化简为
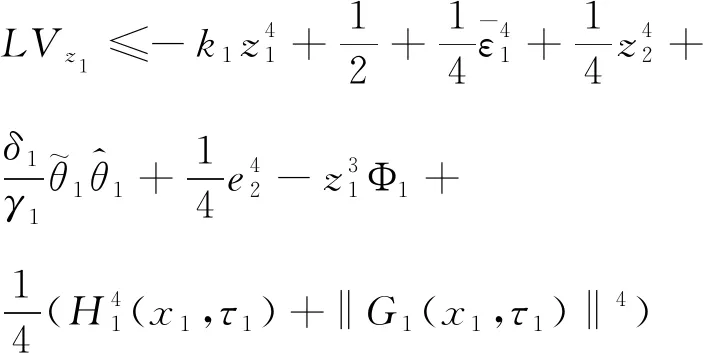
(22)
第i
步(i
=2,…,n
-1):由z
=x
-λ
-ϑ积分可得
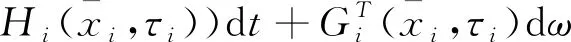
(23)
根据公式(8)~(9)得
de
=

(24)


(25)



(26)

利用神经网络逼近未知函数可得

(27)

使用Young不等式,可得如下不等式
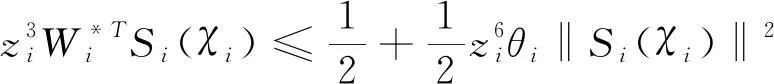
(28)

(29)

(30)

(31)

(32)


(33)

(34)

(35)


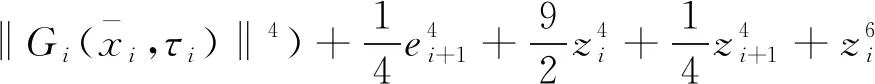
(36)


(37)
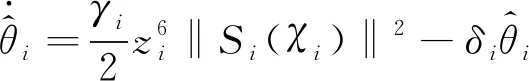
(38)
将公式(37)、(38)代入公式(36)可得

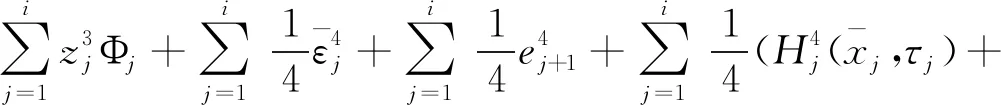

(39)
第n
步:根据公式(7)、(8)可得
(40)
根据公式(8)、(9)得
de
=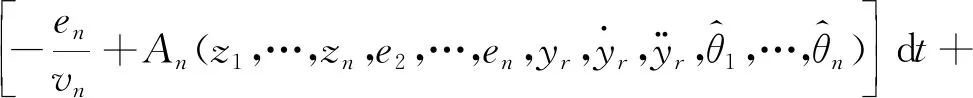
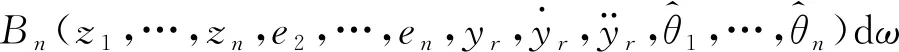
(41)

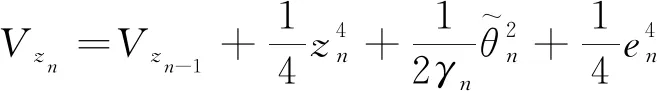
(42)
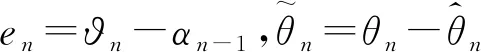


(43)

利用神经网络逼近未知函数可得

(44)


(45)

(46)

(47)


(48)
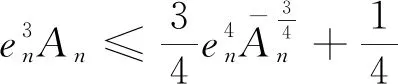
(49)

(50)



(51)

实际控制器和自适应律如下
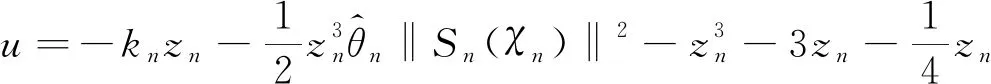
(52)

(53)
类似于公式(39)有

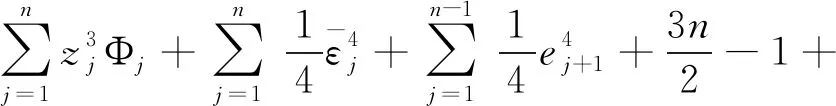

(54)
利用Young不等式可得

(55)
根据文献[19]中假设1,利用引理2得

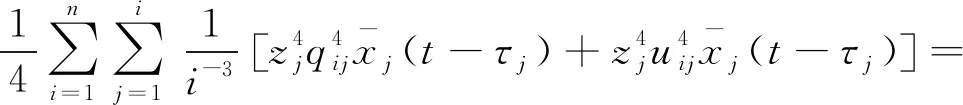

(56)
将公式(55)、(56)代入公式(54)可得
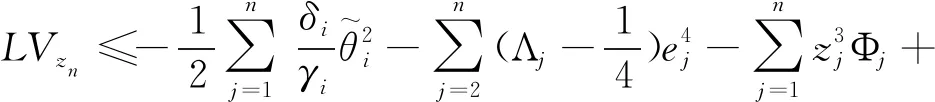


(57)
选择如下Lyapunov-Krasovskii函数
V
=V
+V
(58)
其中:V
定义如下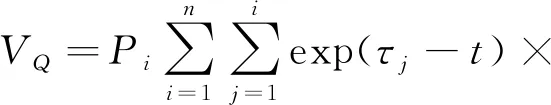
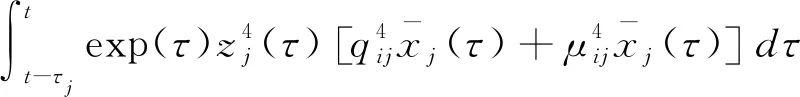
(59)



(60)
由公式(57)~(60)式可得
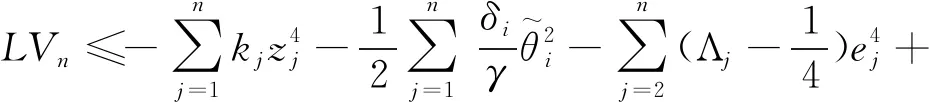
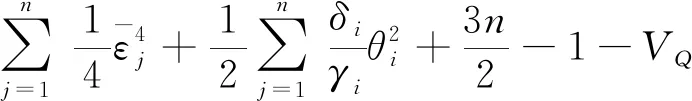
(61)
2.2 闭环稳定性分析
利用公式(11)、(25)、(42)、(58)、(59)可得



(62)
根据公式(61)、(62)易得
L
(V
(t
))≤-Δ
V
(t
)+Δ
(63)
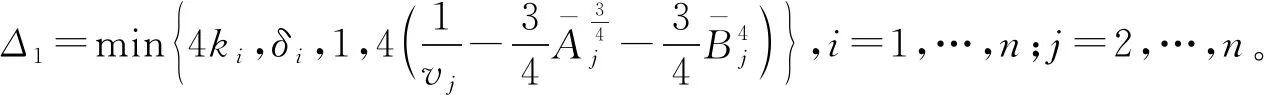

定理1 考虑非线性随机系统(1),基于假设1,设计虚拟控制器(20)、(37)和实际控制器(52),自适应律(21)、(38)和(53)以及滤波器(9),闭环系统所有信号保持半全局依概率有界,且跟踪误差依概率收敛到原点周围任意小的邻域内。
评注1 本文所研究的系统是一个带有输入时延和状态时延的随机系统,实现了该系统有界稳定的跟踪控制目标。作为对比,文献[15]所研究的系统为带有状态时延的随机系统,实现了系统有界稳定的控制目标。文献[17]所研究的系统为带有输入时延的非线性系统,实现了系统有界稳定的控制目标。本文所研究的系统在此二者的基础上分别添加了输入时延和随机扰动,扩展了该系统模型的实际应用范围。
定理1证明如下
根据公式(63),由引理1可得

(64)

u
(t
-τ
(t
))-u
(t
)≤σ
,其中σ
是正常数,令
(65)
对公式(65)求导可得
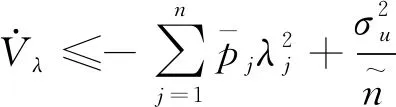
(66)

y
-y
|=|z
+λ
|≤|z
|+|λ
|,即可知跟踪误差也是有界的。自此完成定理1的证明。3 仿真实验
考虑如下的非线性随机时延系统

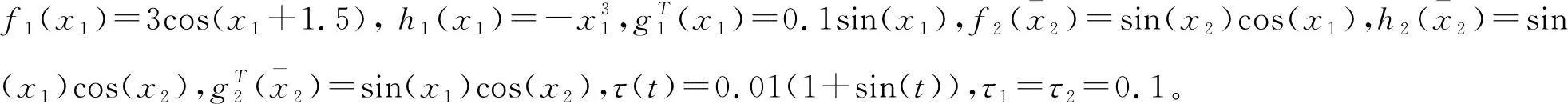
在第一个神经网络中,有144个节点,其中心位于[-3,3]×[-3,3]×[-3,3]×[-3,3]×[-3,3],其高斯函数宽度是Γ=4。 在第二个神经网络中, 有1 728个节点, 其中心位于[-3, 3]×[-3, 3]×[-3, 3]×[-3, 3]×[-3, 3]×[-3, 3]×[-3, 3]×[-3, 3],其高斯函数宽度是Γ=2。


图1 系统输出y和参考轨迹yr

图2 跟踪误差y-yr

图3 控制输入信号u
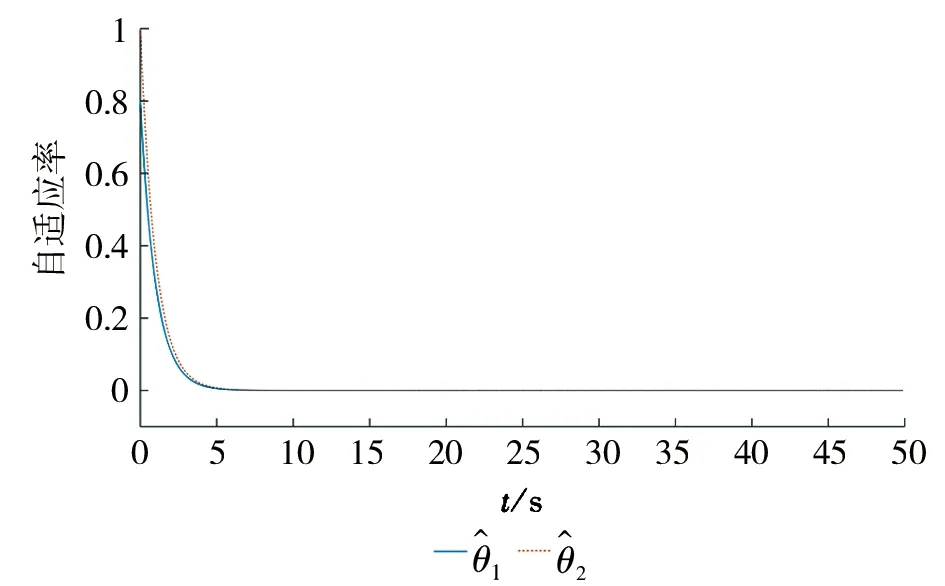
图4 自适应率和

图5 补偿系统状态λ1和λ2
4 结论
(1)针对本文所研究的闭环系统,设计了一个自适应神经网络控制器,并且保证了该闭环系统的所有信号都半全局依概率有界。
(2)本文所设计的自适应神经网络控制器保证了该闭环系统的跟踪误差依概率有界。
