施工工法对双线暗挖隧道应力位移影响研究

2021-10-25韩高彬杜怡韩

安徽理工大学学报（自然科学版） 2021年4期

黄博，曾宇，邹煜，韩高彬，杜怡韩，曹兵

(1. 安徽工程大学建筑工程学院，安徽芜湖 241000；2. 中国矿业大学(北京)力学与建筑工程学院，北京 100083；3. 中铁六局集团北京铁路建设有限公司工程部，北京 100036)

目前隧道施工方法有很多，常用的如明挖法、盾构法与暗挖法，施工工法的选择对地表沉降、围岩稳定性等都有较大的影响，不同工法有其各自的适用范围和优缺点，因而根据实际情况选择合适的施工工法已成为众多工程学者研究的热点问题。

传统的勘测技术由于环境和成本的限制，难以开展进一步研究，数值模拟已成为分析隧道工程相关问题的重要方式之一。文献[7]在四种不同施工方法条件下，通过对收敛量测数据的分析和数值模拟研究判断隧道空间的稳定性；文献[8]采用FLAC软件模拟研究了全断面法、台阶法等4种不同开挖方法对隧道围岩稳定性的影响；文献[9]采用有限元模拟方法，分析了不同方案下地铁隧道同时下穿高铁隧道和铁路桥时的位移特征；文献[10]采用FLAC模拟台阶法施工，得到了不同台阶长度下隧道开挖引起的拱顶沉降和地表沉降规律；文献[11]以近距离交叠区间隧道施工为背景，采用 ANSYS 软件模拟分析了不同开挖工法下地表沉降和地层位移的变化规律；文献[12]针对曲线隧道施工引起的附加应力开展了分析研究，给出了附加应力的解析解，并利用数值模拟的方法进行了对比验证。文献[13]针对水下浅埋隧道、文献[14]针对浅埋双线隧道、文献[15]针对分部开挖的大断面隧道均开展了类似的研究工作。

从目前的研究来看，开挖引起的应力问题研究工作主要集中在隧道工程，而针对地铁车站开挖影响主要围绕位移问题。因此，本文依托实际工程，利用软件建立双线隧道数值计算模型，通过开展数值模拟工作，对不同施工方法下该双线暗挖隧道的应力场和位移场分布特征进行对比分析，绘制三维应力场、位移场分布图，确定其在不同施工工法影响下的应力、位移响应，以期为今后类似的双线隧道暗挖工程提供一些理论依据和参考。

1 数值模型的建立

1.1 工程背景

北京地铁七号线黑庄户站～万盛南街西口站区间为一双线暗挖隧道工程，部分区间段采用矿山法施工。矿山法隧道标准断面采用马蹄形断面，宽6.5m、高6.8m，初期支护采用格栅钢架加喷射混凝土，双线隧道间距取最小值6.5m。

1.2 模型建立

双线隧道覆土厚约16m，主要穿越的土层为粉质黏土、细砂、中砂和粗砂。研究中涉及的土层及初衬结构的物理力学参数详见表1，根据工程背景建立的数值模型如图1所示，不同颜色分别代表相应的四个土层。

表1 土层及初衬结构参数表

图1 数值模型

为了充分反映每个层面上的应力场分布，并考虑模型的尺寸和边界效应，模型尺寸定为80m(横向、

坐标轴)×20m(纵向、

坐标轴)×33m(高度、

坐标轴)，并在模拟中固定了前、后、左、右和底面。“窄长”的尺寸设计使其更贴近研究平面应变问题的条件。

1.3 监测点布置

如图2所示，在模型的顶部沿

方向每隔2m设置一个沉降监测点，隧道周围的关键部分设置了变形监测点，编号P1～P8。与此同时，选取隧道拱顶所在平面为特征平面P，设置位移和应力监测点，用于研究该区域的应力场与位移场的分布。

图2 关键监测点分布

1.4 模型验证

为提高数值模拟结果的可靠性，现通过对现场施工过程进行数值模拟加以验证，现场采用的是台阶法施工。利用模型关键监测点的沉降值与现场相应位置监测记录的沉降值进行对比，以验证模型的可靠性。如图3所示，选取了现场地表沉降中心监测点和隧道A拱顶沉降监测点进行对比。可以看出，数值模拟结果与现场监测数据总体沉降规律近似相同，沉降量也基本吻合。因此，可以采用此数值模型开展进一步研究。

图3 实际沉降与模拟沉降对比

2 开挖方案设计

本次研究共设置了两大类、涉及3种开挖工法的方案，两大类之间差别在双线隧道的开挖错开距离，3种开挖工法分别为全断面法、台阶法和CD法。

第一大类方案为先开挖隧道A，待隧道A开挖至20m贯通后再开挖隧道B，最终完成开挖。在开挖过程中分别模拟以上3种工法，并对引起的应力、变形进行对比；第二大类为现场施工比较常见的一种方案，即先开挖隧道A，待隧道A开挖10m后便开始开挖隧道B，由于导洞开挖错开的距离小，整体工期相对较短，施工组织紧凑，因此施工效率较前一类高，研究方法和内容与第一大类方案相同。

3 隧道应力和位移分布规律

3.1 第一类方案模拟结果

1)应力分布规律。绘制了采用第一类方案时，隧道拱顶特征平面P的三维应力场分布图，如图4所示。可以看出，采用不同的开挖方法时，监测平面P上的应力分布均呈现明显的峰值和谷值区域，但峰、谷值等有所差别。

（4）建立与海事处联动机制：台风来临前惠州海事局指挥中心要加强与相关海事处的联动，加大电子巡航和现场巡航的能动作用，有效控制非本港船舶进港避风，特别是那些提前量很大的船舶坚决不允许进港，在台风来临前要求海巡船到现场巡航和驱离，严格控制本港避台船舶的数量，以免由于避风船舶数量太多使锚地拥挤而造成更多船舶险情。

(a)全断面法

采用全断面开挖，如图4(a)所示，监测平面上呈现出2个明显的谷值区域，即双线隧道开挖引起的应力释放，相应的在双线隧道中间区域和两边外侧区域则形成了峰值区域，外侧无影响区域竖向应力均值323.6kPa，受影响区域竖向应力极值403.1kPa，应力集中系数为1.246；采用台阶法开挖，如图4(b)所示，其应力场的分布与全断面相似，其竖向应力极值403.3kPa，应力集中系数为1.246，与全断面开挖结果相同；采用CD法开挖，如图4(c)所示，相比前两者，双线隧道中间区域的应力较为缓和，竖向应力极值397.1kPa，应力集中系数为1.227。

综上，CD法形成的应力场，应力集中程度最小，分布较为缓和，即从应力分布规律的角度来看，为最优开挖方法。

2)位移分布规律。图5为采用第一类方案时的位移监测结果，其中图5(a)～(c)图为特征平面P的位移场分布情况，分布规律差别较为明显。图5(a)所示，采用全断面法开挖时，两隧道拱顶的沉降分布情况相似、较为对称，后开挖的隧道B拱顶区域沉降要略大于先开挖的隧道A，最大沉降值为46.9mm。采用台阶法开挖时，如图5(b)所示，先开挖的隧道A拱顶区域沉降要明显大于隧道B，沉降分布区域要比全断面法分布范围广，最大沉降值51.0mm。相比于前两者，采用CD法开挖时，如图5(c)所示，引起的沉降值明显较低，最大沉降值为33.3mm，且沉降主要发生在每条隧道两侧，不集中于隧道中心线区域，这与其左右分步开挖的方式有直接关联。

(a)全断面法

图5(d)为地表沉降曲线，由图可知，台阶法引起的地表沉降最大，最大沉降值为20.5mm，全断面法次之，为13.3mm，CD法引起地表沉降最小，为6.2mm。最大地表沉降位置也有所不同，全断面法开挖时，位于两隧道正中间的上方，沉降曲线较为对称；台阶法开挖时，位置偏向于先开挖的隧道A上方；CD法开挖时则相反，偏向于后开挖的隧道B的上方。

进一步分析隧道A、B周围关键点的位移变化情况，发现CD法施工后周围监测点的变形量最为均匀、总体较小，均在0～10mm范围内；台阶法周围各监测点变形量相差较多，变形量也最大，隧道A顶部P1点最大沉降达32mm，为所有监测点数据最大值，详见3.3节表2；全断面法引起的位移量则居中，测点变形量相对于台阶法较均匀。需要说明的是，3.3节表2中CD法P1点沉降出现正值主要是与建立的模型和数值模拟本身有关，在隧道上方模型土体厚度有限时，CD法施工模拟中由于支护强度足，运算结果会出现一定的向上位移，但此现象不影响对CD法控制拱顶沉降方面优势的判断。

综上所述，采用第一类方案开挖时CD法引起的位移量总体而言是最小的，位移场分布也较为均匀。从位移分布规律的角度来看，也应为最优的开挖方法，与应力分析结果统一。

3.2 第二类方案模拟结果

(a)全断面法

全断面开挖时，如图6(a)所示，受影响区域竖向应力极值403kPa，应力集中系数为1.246，与第一类方案相同；采用台阶法开挖时，如图6(b)所示，竖向应力极值402.5kPa，应力集中系数为1.244，较第一类方案略有下降；采用CD法开挖时，如图6(c)所示，竖向应力极值398.4kPa，应力集中系数为1.231，较第一类方案略有上升。

综上，CD法形成的应力场，应力集中程度依旧最小，分布较为缓和，与第一类方案的结论相统一，结果与第一类方案差别较小，可认为开挖错开的距离对最终的应力场分布影响不明显。

2)位移分布规律。图7为采用第二类方案时的位移监测结果，分布规律类似于第一类方案，但部分工法下沉降值变化明显。如图7(a)所示，全断面法开挖时，最大沉降值为46.9mm，与第一类方案差别不大。台阶法开挖时，如图7(b)所示，最大沉降值47.7mm，比第一类方案下降了3.3mm。CD法开挖时，如图7(c)所示，最大沉降值为41.5mm，比第一类方案增加了8.2mm。

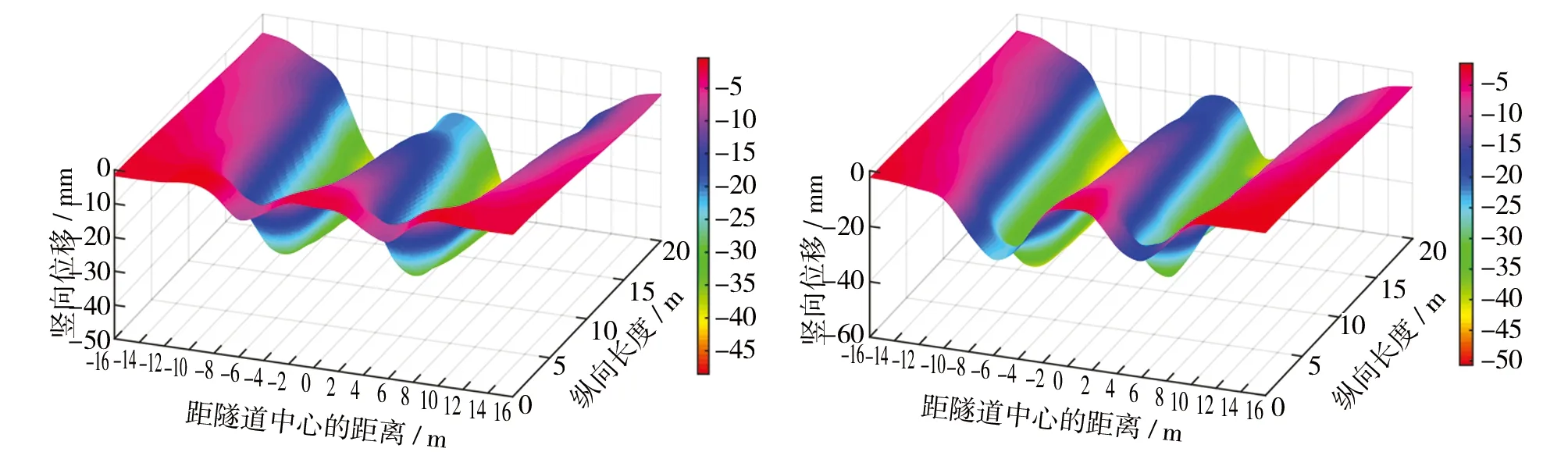
(a)全断面法 (b)台阶法

地表沉降的监测结果，如图7(d)所示，台阶法引起的地表沉降依旧最大，最大沉降值为17.4mm，相比于第一类方案下降了3.1mm；全断面法次之，为13.4mm，相比于第一类方案上升了0.1mm；CD法引起地表沉降最小，为8.1mm，相比于第一类方案增加了1.9mm。

进一步分析隧道A、B周围关键点的位移变化情况，模拟结果类似于第一类方案，主要差别在台阶法P1点最大沉降，为25mm，低于第一类方案。

3.3 模拟结果对比与分析

从上述两大类开挖方案的模拟结果可知，施工工法不同，对隧道周围土体的应力场分布影响不显著，但对土体变形影响较为明显。表2给出了两大类方案各三种施工工法在特征平面P上的应力集中系数，可以看出两大类方案的结果之间差别很小，三种工法中CD法的应力集中系数最小。CD法由于临时中隔墙的存在，横向开洞尺寸较小，仅为其他两种工法的一半，从而在竖直平面内引起的竖向应力集中现象最不明显，应力集中系数也最小。

表2同时汇总了两大类方案的变形结果，从大类比较可以看出，第二类方案对CD法位移结果的影响较大，由于同时会有4个导洞施工，相互影响明显，因此位移较第一类方案有一定程度地增加。3种工法之间对比，可以清楚地看出CD法在引起位移方面的优势，缘于其开挖断面小、临时支撑强；同时，也可以看出台阶法虽然一次断面开挖较小，但由于在土层中初次支护封闭时间长，因此在双线隧道开挖时需要特别注意初期支护封闭时间的控制，否则不利于土层的稳定性。全断面开挖则相对处于前两者的中间状态。