极限状态下的加筋土挡土墙设计研究
2021-10-24吴炫
吴 炫
华设设计集团股份有限公司,江苏 南京 210014
极限状态设计方法是基于可靠度理论发展起来的,1980年我国颁布了相关技术标准,使该理论在路基、桥梁、隧道等工程中广泛应用,为极限状态设计方法的发展起到了促进的作用。我国对于极限状态理论的研究起步较晚,从理论分析初期至今未形成健全的理论系统。文章基于挡土墙的影响因素的相关系数指标对挡墙进行验算,推理得到有效的挡墙极限状态方程,根据初步确定的目标可靠度可以计算出有关加筋土挡土墙的表达式,为我国公路中路基的挡土墙结设计构提供有效的分析方法和可靠的理论计算依据。
1 极限状态设计方法
1.1 可靠度理论
可靠性概念定义是路基支挡结构的挡土墙在规定的使用条件和使用时间内,实现结构物自身预定功能的安全性,对结构物安全性、适用性、耐久性进行总体的评价。换言之,结构可靠度的标准是结构物在规定时间和条件下的安全性、耐久性、适用性的性能得到保证。
可靠度表示支挡物或构造物在规定的条件下和时间内,实现结构自身预定功能的能力,通过字母Ps来表示。可靠概率是对可靠度进行定量的描述,通过该指标可对可靠度进行评价。相反,失效概率是指支挡物或构造物在规定的条件、时间内不能完成预定功能的概率,通过字母Pf来表示。支挡物的失效概率与可靠概率二者相互独立、互不相容,通过以下公式表达:

支挡结构应保证在设计使用年限内以较为合适的可靠度来满足规定的要求,支挡结构要满足可靠度的要求应满足以下功能:第一,正常施工、正常使用条件下,支挡物或结构物能承受自身重量和外界荷载等作用;第二,结构物受到偶然荷载的作用,结构仍能够保持整体稳定性;第三,正常使用条件下的结构物能够保持很好的工作性能;第四,结构具有足够的耐久性。以上条件中,第一条和第二条是承载能力要求,属于结构的安全性范畴;第三条表达的是结构的适用性;第四条表达的是结构的耐久性。以上条件均是正常使用的要求。
1.2 极限状态设计表达式
挡墙在极限状态下时,设计表达式的分项系数,为挡墙支护结构提供可靠的储备,采用极限状态研究方法,挡墙各参数的性能计算表达式如下。
抗倾覆检算的极限状态设计表达式:


抗滑动检算的极限状态设计表达式:

式中:f为摩擦系数。
抗拉检算的极限状态设计表达式:
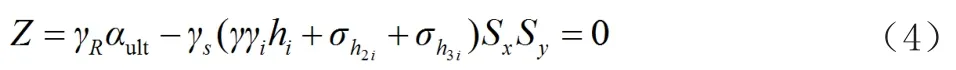

抗拔检算的极限状态设计表达式:

2 极限状态方程
2.1 路肩式加筋土挡土墙
(1)抗拔稳定性分析。加筋土挡土墙的抗拔稳定性采用两种荷载情况进行分析,一种是挡土墙有荷载的情况,另一种是无荷载的情况,还应对加筋土挡土墙单根拉筋的抗拔力进行计算。加筋土挡土墙受力稳定性分析如图1所示。

图1 内部稳定分析图(路肩式)
无荷载作用状态时,挡墙抗拔性能状态表达式为
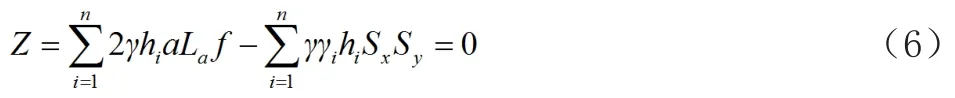
式中:a为筋带宽度,m;La为筋带锚固段长度,m;hi为路基顶至第i层填料的距离,m。
极限荷载作用时,挡墙抗拔性能的状态表达式为
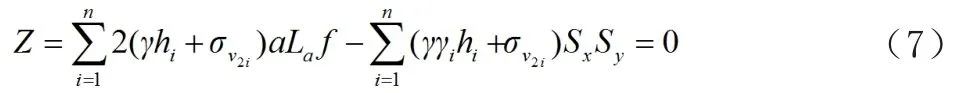
(2)抗拉稳定性分析。极限无荷载作用状态时,挡墙抗拉性能的状态表达式为

极限荷载作用时,挡墙抗拉性能的状态表达式为

2.2 路堤式加筋土挡土墙
路堤式加筋土挡土墙与路肩式加筋土挡土墙的不同之处在于墙上增加了填土,应对其进行土柱的换算。其内部稳定分析图如图2所示。

图2 内部稳定分析图(路堤式)
(1)抗拔稳定性分析。有荷载作用下,路堤式加筋土挡土墙抗拔稳定性的极限状态方程同公式(5)。
(2)抗拉稳定性分析。有荷载作用下,路堤式加筋土挡土墙抗拉稳定性的极限状态方程同公式(5)。
3 挡墙分项系数取值
通过蒙特卡罗法对荷载以及抗力的标准差和变异系数进行相关统计,最后通过一般分离法对分项系数进行计算。通过分项系数的计算结果可知,该系数的收敛性较好,可以作为分项系数的建议采取值。对计算结果以及统计值进行分析可以看出,加筋土挡土墙的抗拔分项系数在不受荷载作用的情况下大于加荷载作用的情况下的分项系数;加筋土挡土墙的抗拉分项系数无荷载作用的情况小于有荷载作用的情况。综合分项系数如表1所示。

表1 综合分项系数
4 极限状态设计表达式
通过计算结果可知,挡土墙的分项系数具有一定的可靠性。将该系数作为分项系数的建议值时,其极限状态设计的表达式如下。
路肩式筋带抗拔表达式:

式中,分项系数γR=0.506,γS=1.16。
路肩式筋带抗拉表达式:

式中,分项系数γR=0.819,γS=1.235。
路堤式筋带抗拔表达式:同公式(5)。
式中,分项系数γR=0.514,γS=1.166。
路堤式筋带抗拉表达式:同公式(4)。
式中,分项系数γR=0.815,γS=1.269。
5 结论
文章通过对极限状态下的挡墙设计进行分析研究得出以下结论:(1)挡土墙的可靠度指的是在规定的条件、时间内,实现结构自身预定功能的能力;(2)文章通过对路堤式加筋土挡土墙和路肩式加筋土挡土墙的抗拉性能和抗拔性能进行分析,得到了各自对应的极限状态方程;(3)分项系数为结构本身提供了安全储备,因此文章通过对分项系数的研究,对分项系数进行了统计分析,得出了综合分项系数。对统计值进行分析得到结论:不加外荷载抗拔稳定性、极限加载抗拉稳定性满足要求。该结论与极限状态假设挡墙的受力情况计算结果相符,表明此研究中的分项系数取值合理。
