不同海拔高度下γ射线空气衰减系数的计算

韦凯迪，徐 阳，高 飞，刘川凤，杭仲斌，王子琳

(中国原子能科学研究院 计量与校准技术重点实验室，北京 102413)

近年来，利用无人机进行空中辐射监测的需求日益增加[1-2]。我国核电发展迅速，与之相应的核应急监测也得到了政府部门和核电企业的重视，而一些核工业生产和运营单位缺乏快速的事故应急监测设备，很难在第一时间确定事故等级和获取监测数据[3]。利用无人机辐射监测系统(以下简称系统)在核设施及环境周边进行航测具有重要意义，是未来发展的必然趋势[4-5]。同时，还可利用无人机进行环境天然辐射本底测量、地质勘察[6]、寻找放射源[7]、海港口岸辐射监测[8]、放射性烟云跟踪、核事故应急及事故后处理后期环境监测与评价等航空辐射监测。在航测过程中，由于不同海拔高度下空气密度不同，γ射线在空气中呈指数衰减，因此需要考虑不同空气密度下的空气衰减，并进行衰减修正。本研究采用经验公式计算不同海拔条件下的空气密度，并利用蒙特卡罗(以下简称蒙卡)法建立γ谱仪模型，模拟不同高度下粒子注量，并计算不同海拔条件下的线衰减系数。在γ射线参考辐射场中利用衰减板进行空气等效衰减实验，对参考辐射场中不同高度处剂量率进行测量，并通过衰减公式计算137Cs源、60Co源的线衰减系数，将模拟结果与实验测量结果进行对比分析。

1 气压、温度与海拔高度的关系

不同海拔高度对大气温度和压强有一定影响，从而造成空气密度不同，温度和气体压强的综合变化可导致空气密度发生高达30%的变化。因此飞行器在飞行测量过程中需要考虑不同气温和气压对高度修正系数的影响。国家能源局发布了《中华人民共和国电力行业标准：火力发电厂燃烧系统设计计算技术规程(DL/T 5240-2010)》[9]，DL/T 5240-2010给出的海拔高度与大气压强之间的经验公式如下：

Pa=101.3×

(1)

式中：Pa为当地平均大气压强，kPa；H为当地海拔高度，m。

在计算过程中，统一用青岛零点作为各地海拔高度的水准零点。海拔越高，大气压强P越低，但在海拔4 000 m以内，海拔高度每上升500 m，大气压强下降的相对值为5.79%～6.25%，因此在100 m以下，大气压强的下降值相对较少，可以认为是相对平衡状态。

随着海拔高度上升，大气温度明显下降，海拔高度每升高100 m，温度降低0.5 ℃ 左右[10]，海拔高度与温度的关系见公式(2)：

t=15-0.006 5H

(2)

式中：t为不同海拔高度的温度，℃；H为当地的海拔高度，m。

2 空气密度的计算

大气压强和温度的变化导致空气密度的变化，可根据不同气压和温度求出空气密度，见公式(3)：

(3)

式中：ρ为大气压强为P时的大气空气密度，kg/m3；ρ0为标准状况下(0 ℃，101 kPa)的空气密度，取1.293 kg/m3；t为实际的大气温度，℃；P为实际的大气压强，kPa。

我国地势西高东低，同时从西部青藏高原到东部沿海大陆架，呈明显的三级阶梯状分布[11]，鉴于我国特殊地理形式，根据公式(1)、(2)、(3)计算海拔4 500 m以下的海拔高度与大气温度、气压、密度之间的值，根据公式(3)计算出的空气密度列于表1。不同海拔高度与空气密度的关系示于图1。从图1中可以看出，空气密度随海拔高度的增高而降低。

3 不同密度条件下的空气衰减蒙卡模拟

3.1 γ谱仪模型建立

利用MCNP软件建立γ谱仪模型。源点处分别放置137Cs源和60Co源，为了降低方差和提高效率[12]，将整个球壳外部的电子和光子的重要性设置为0。利用F4卡计算位置1和位置2处的γ光子注量，如图2所示。利用137Cs、60Co源平行束作为源项进行平行束发射，γ射线与空气发生光电效应、康普顿散射和电子对效应，在空气中发生衰减并服从指数衰减规律[13]，如公式(5)所示：

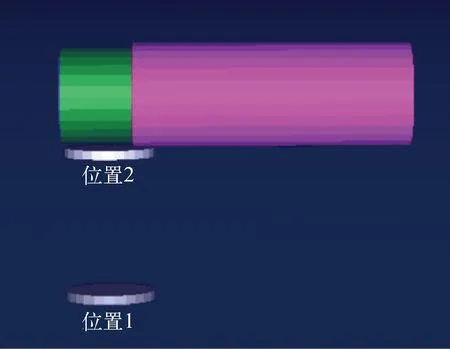
图2 MCNP模拟示意图Fig.2 MCNP simulation diagram

Ih=I0e-μh

(5)

式中：Ih，I0分别为测量高度(位置2)和地面0 m高度(位置1)处的注量，cm-2；h为经气压、温度修正后的有效高度，m；μ为不同高度处空气的线衰减系数，m-1。

由公式(5)推出光子的空气线衰减系数为：

(6)

3.2 线衰减系数计算

利用蒙卡模拟计算出不同高度处γ光子的注量，并根据公式(6)计算得出以青岛为水准零点的海平面附近到西藏那曲海拔4 507.5 m之间的线衰减系数，在实际应用时用插值法进行计算得到待测当地的线衰减系数。在航空γ剂量率测量时，需要给出地面1 m处的剂量率[14]，不同海拔高度离地1 m处线衰减系数示于图3。

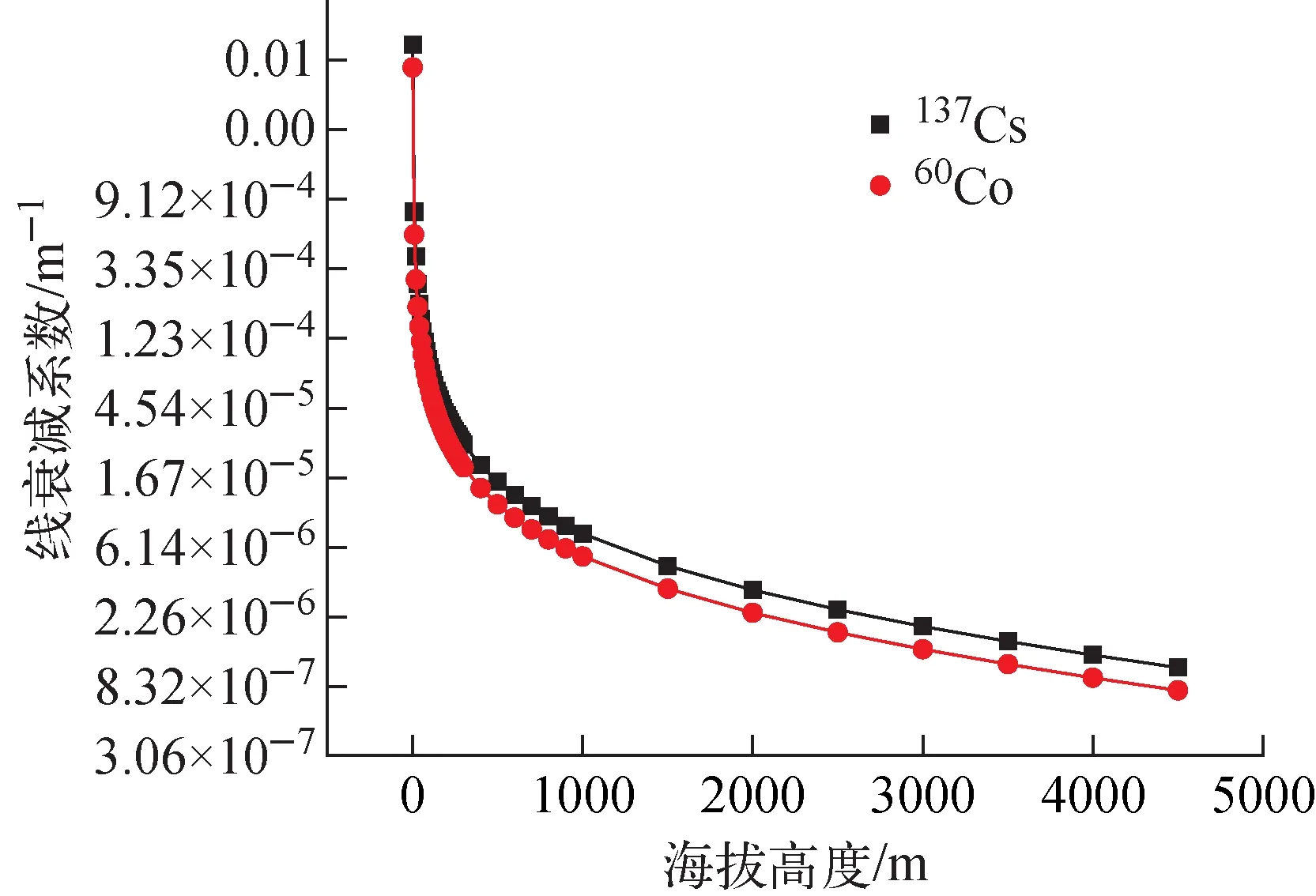
图3 不同海拔离地1 m高处的线衰减系数Fig.3 Linear attenuation coefficient at different altitudes 1 m above the ground

模拟计算海拔高度1 m处的空气质量衰减系数与美国国家标准和技术研究院(NIST)官网推荐的数据进行对比，结果列于表2。由表2可以看出，由经验公式求出的空气密度模拟得出的空气质量衰减系数与美国NIST推荐值最大误差为-17.3%。

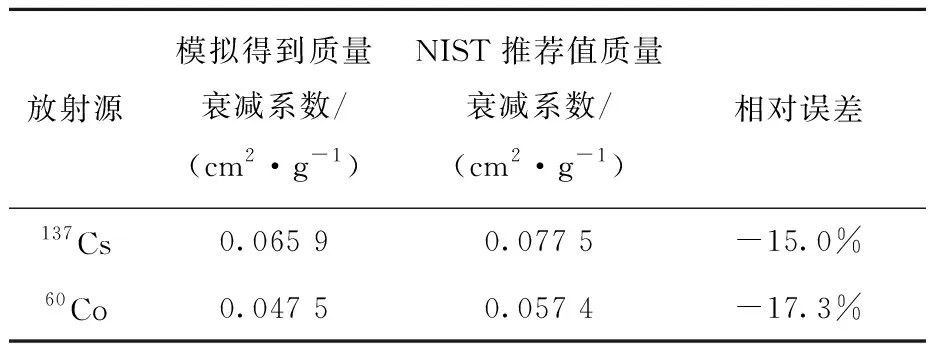
表2 模拟值与NIST推荐值比较Table 2 Comparison of analog values with NIST recommended values

4 参考辐射实验验证

4.1 实验装置搭建

在参考辐射场中开展实验，并将蒙卡模拟值与线衰减系数的实验测量值进行对比。聚甲基丙烯酸甲酯(polymethyl methacrylate, PMMA)易于加工，且对于伽马射线的衰减系数较大，实验过程中选用PMMA有机玻璃(密度1.18 g/cm3)作为空气等效材料，在137Cs和60Co参考辐射场中进行衰减实验验证。查询NIST官网得出有机玻璃在137Cs源参考场中的线衰减系数为0.098 813 cm-1，在60Co源参考场中的线衰减系数为0.073 095 cm-1。将不同厚度的衰减板放置在放射源和电离室之间，模拟等效不同高度的空气，实验现场布置图示于图4。

图4 空气等效衰减实验现场布置图Fig.4 Schematic diagram of the experimental layoutof the equivalent air attenuation

实验中选取PTW 32005球型电离室，球体半径为2.2 cm。将电离室测量点放置在出射束中心轴线上，光束可全部覆盖电离室的测量体积。通过移动小车位置改变与放射源的位置，获得不同位置处的空气比释动能率。根据上述布置要求，模拟空气等效衰减实验布置示意图示于图5。

通过指数衰减公式(7)计算得出距源空气厚度为dair处的剂量率Iair(mGy/h)：

Iair=I0e-μair dair

(7)

式中：I0为参考辐射场中未加衰减板测得的剂量率，mGy/h；μair为空气的线衰减系数，m-1；dair为源距探测器的距离，m。

4.2 实验验证结果

137Cs源、60Co源模拟数据与空气等效测量数据结果分别列于表3、表4。在相同剂量率I0条件下，将PMMA衰减板置于源出射口处，并将电离室放置在参考点处进行测量，通过插值法求出PMMA衰减板的线衰减系数，并计算出PMMA衰减板的厚度，经过测量得到衰减后的剂量率IPMMA，如公式(8)所示：

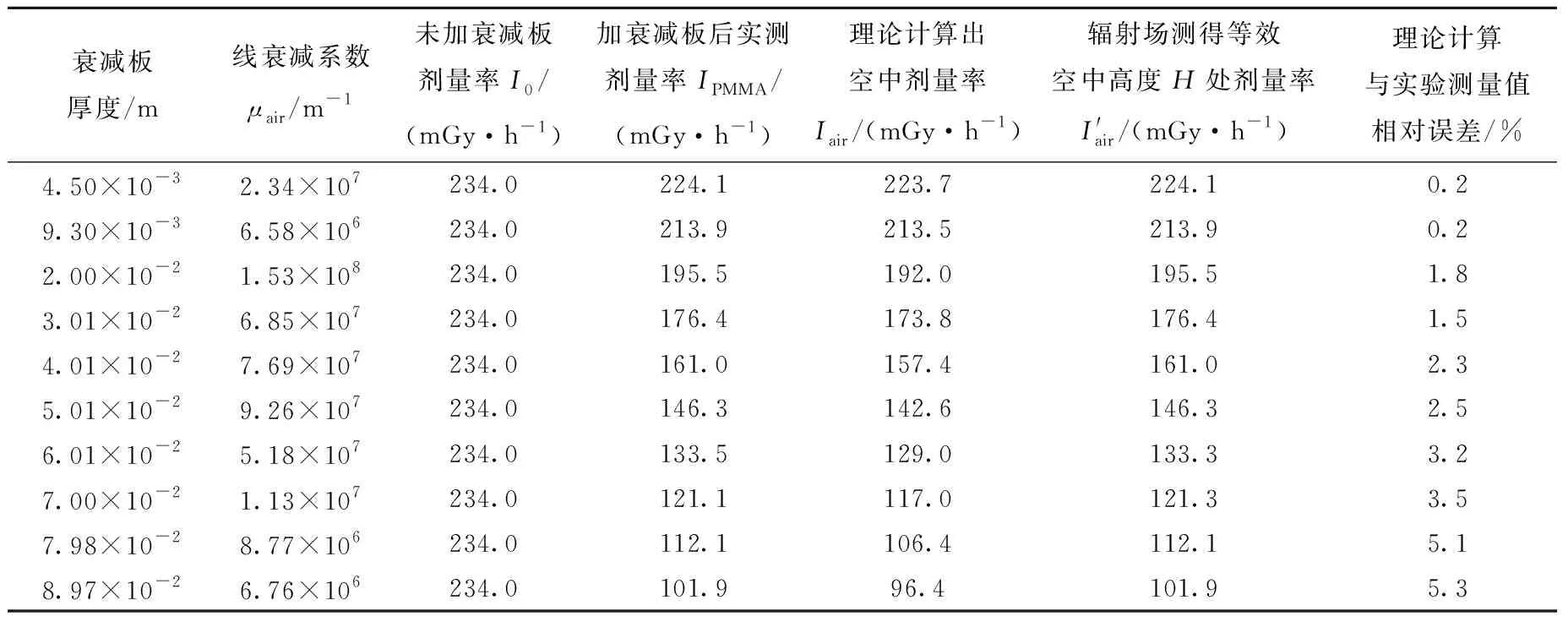
表3 137Cs源模拟数据与空气等效测量数据对比Table 3 Comparison of 137Cs source simulation data and air equivalent measurement data

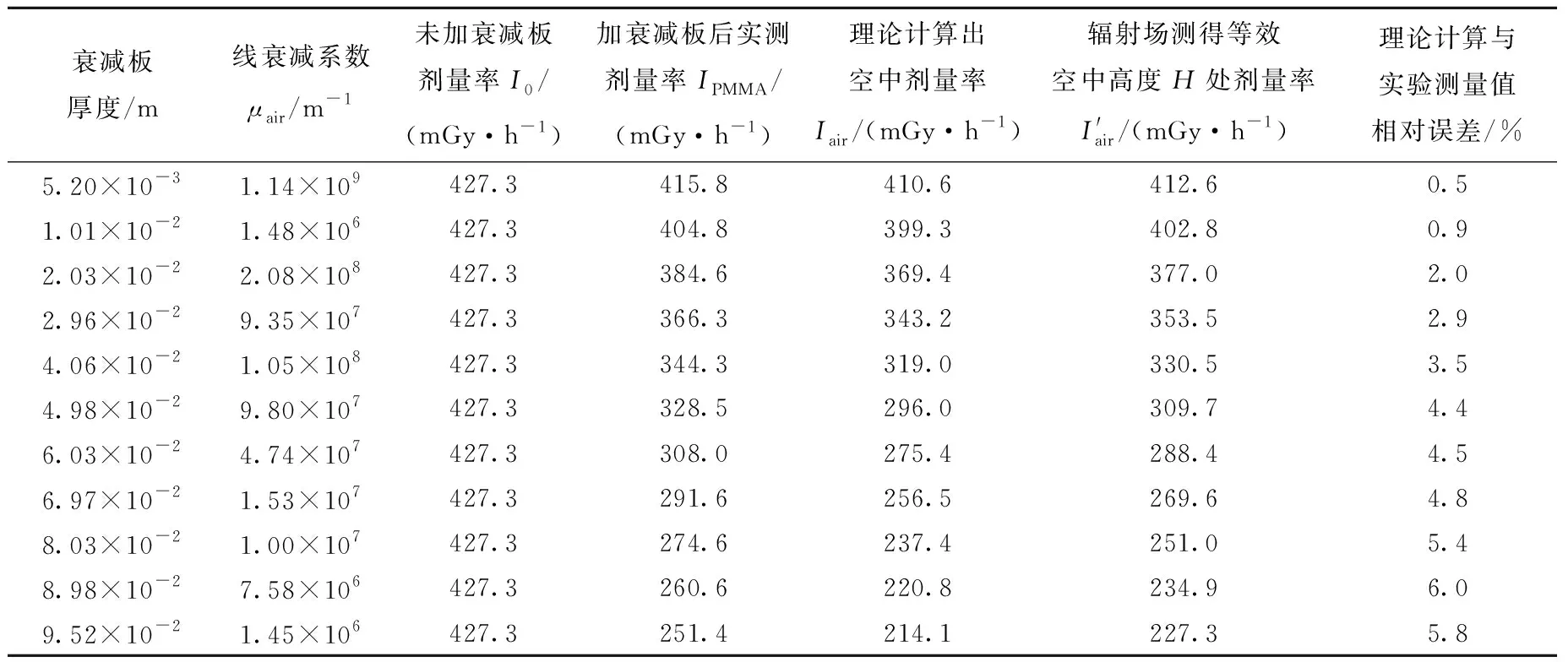
表4 60Co源模拟数据与空气等效测量数据对比Table 4 Comparison of 60Co source simulation data and air equivalent measurement data

IPMMA=I0e-μPMMA dPMMA

(8)

式中：μPMMA为PMMA衰减板的线衰减系数，m-1；dPMMA为PMMA衰减板厚度，m。由公式(7)、(8)联立推出参考辐射场中等效距源空气厚度为H高度处的剂量率为：

Iair=IPMMAe(μPMMA dPMMA-μair dair)

(9)

参考辐射场中实际测量得到的剂量率等效成距源空气厚度为dair处的剂量率I′air与理论计算出的空中剂量率Iair的相对误差为：

(10)

通过表3、表4实验数据分析可知，在137Cs源时，通过理论计算得出的模拟空中剂量率与等效空气实验实测的剂量率最大相对误差为5.3%，60Co的最大相对误差为6.0%，因此可以用于低空近地辐射监测工作。

5 结论

不同海拔条件下空气密度不同，因此造成γ射线空气线衰减系数不同。利用MCNP法对γ射线空气线衰减系数进行模拟计算，得出的空气质量衰减系数与美国NIST官网推荐值进行比较，最大相对误差为-17.3%。利用有机玻璃作为衰减板，在参考辐射场中进行模拟空中等效衰减实验验证，最大相对误差为6.0%。模拟结果和实验结果表明，在本工作中所涉及的137Cs和60Co源能量范围内，模拟计算出的空气线衰减系数满足相关要求，为低空近地辐射剂量监测提供了理论依据，可保证测量结果的准确性。