内燃动车组动力包振动烈度全局灵敏度研究
2021-10-22孙维光张文瀚张立民
孙维光,郑 伟,张文瀚,张立民
(1.中车青岛四方机车车辆股份有限公司,山东 青岛266311;2.成都勘测设计研究院有限公司,成都611130;3.西南交通大学 牵引动力国家重点实验室,成都610031)
内燃动车组是以柴油发电机组(简称机组)为动力源的一种铁路运输工具,广泛用于山区铁路和非电气化铁路上。随着内燃动车组运行速度的提高,车辆及其附属设备(这里主要指动力包机组)系统的振动问题也日益显著。由于车内安装空间的限制以及集成化要求,机组及其它附属设备被弹性安装在一个基础框架上,框架通过两级隔振器与车体底架相连,从而构成了动力包双层隔振系统。动力包机组在工作状态下产生的振动不仅会影响动力包内部设备的振动状态,而且会通过隔振器传递到车体,降低乘客的乘坐舒适性体验,因此动力包隔振参数设计是内燃动车组设计中不可或缺的一环。
为估计各参数对目标的影响程度,1993年Sobol[1]提出了一种以方差为基础的全局灵敏度方法,提高并推动了全局灵敏度分析的计算效率和发展。后来Homma 等[2]对Sobol 法进行了完善,提出了一种总体全局灵敏度评价指标。李睿[3]将Sobol总体灵敏度法与局部灵敏度分析法用于研究结构参数对非线性隔振系统隔振效率的灵敏度。聂祚兴等[4]应用Sobol 法对汽车噪声传递函数进行了灵敏度分析,在此基础上对车辆参数进行了多目标优化设计。姜亚楠等[5]将Sobol 法应用到飞机整体翼梁结构损伤容限的设计中,提高了设计效率。Qin等[6]建立了非线性车辆模型,提出了两步全局灵敏度分析法,并将其应用于车辆参数的灵敏度分析中。由此可见,全局灵敏度方法已经在多种隔振系统中得到应用,但是在对车下吊挂动力包的灵敏度分析及优化设计中却少有应用。本文推导基于Sobol 全局灵敏度分析方法的动力包悬挂参数灵敏度计算方法。借助于这一方法计算动力包各个转速工况下振动烈度Vrms关于动力包悬挂参数的全局灵敏度Svy,分析对Svy影响较大的悬挂参数,为动力包隔振参数优化设计奠定了基础。
1 Sobol全局灵敏度分析原理
Sobol 全局灵敏度分析方法是一种基于方差分析的蒙特卡洛法,其原理是利用积分法将目标函数f(X)分解为单个参数和参数间相互组合的函数,通过采样技术计算单个参数或组合参数集的方差对模型响应总方差的影响,从而分析该参数及参数之间交互作用的重要性。原理如下:
设模型目标函数为f(X),将其分解为2k项递增项之和:
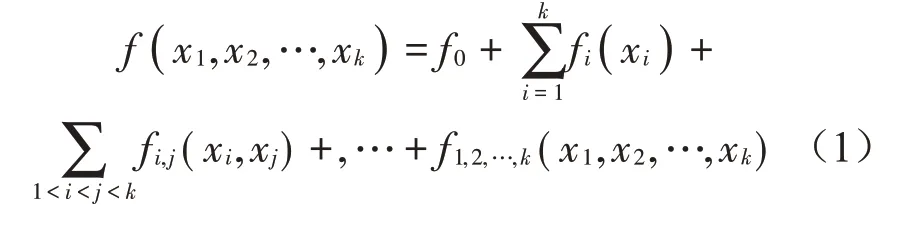
式中:f0为常量,其余子项对其所包含的任意参数的积分一定为零,即:

式中:z表示子项。因为各子项两两正交,由(1)和式(2)可推出各子项可以表示为f(X)的积分形式:
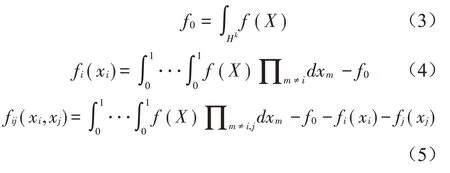
定义目标模型函数f(X)的总方差D为:

各项子式的偏方差为:
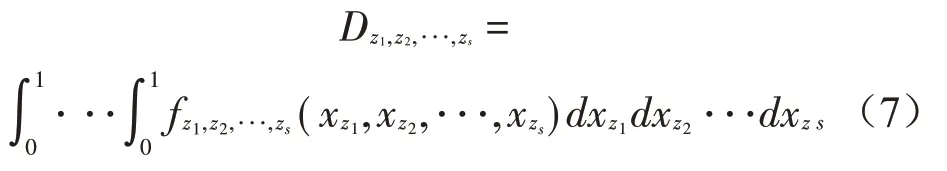
式中:1≤z1≤…≤zs≤k,且s=1,2,…,k。通过对式(1)平方并在整个定义域Hk内积分,结合式(2)可得:
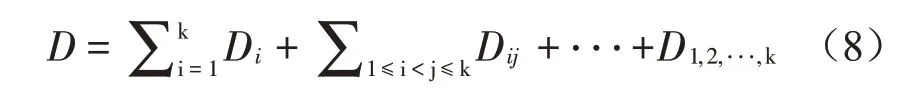
Sobol全局灵敏度系数定义为:
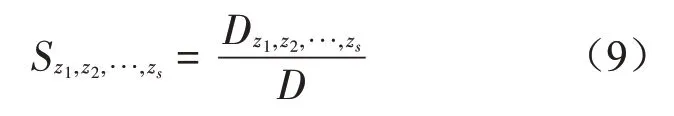
式中:Si(i=z1z2…)为第i个参数的1阶全局灵敏度,表示参数xi的变化对目标函数输出结果的影响,Si,j(i≠j)为2阶全局灵敏度,表示参数xi和xj同时变化对目标函数输出结果的影响,以此类推可以得到参数xi与其它所有参数交互作用产生的各阶灵敏度。
2 动力包机组振动烈度及其灵敏度计算方法
2.1 动力包机组振动烈度函数
内燃动力包主要由柴油发电机组、冷却装置、安装框架以及隔振装置等部件构成,动力包双层隔振系统结构示意图如图1所示。
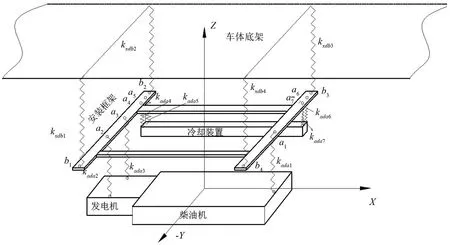
图1 内燃动力包双层隔振系统示意图
运用动力学理论建立动力包双层隔振系统振动方程表达式如下:

式中:M、K、C为系统的质量、刚度与阻尼矩阵;P为载荷矢量;X¨X˙X分别为系统的振动加速度矢量、速度矢量和位移矢量。其中:

Xoi,Yoi,Zoi,i=1,2,3——分别表示框架、机组和冷却装置沿X,Y,Z方向平动的自由度。
αoi,βoi,γoi,i=1,2,3——分别表示框架、机组和冷却装置绕X,Y,Z轴的转动的自由度。
Moi,i=1,2,3——分别表示框架、机组和冷却装置的质量,单位kg;
JXoi,JYoi,JZoi,i=1,2,3——分别表示框架、机组和冷却装置绕X轴、Y轴和Z轴转动惯量,单位kg·m2;ki,j=K(Kzda1,Kzda2,Kzda3,Kzda4,Kzda5,Kzda6,Kzda7,Kzdb1,Kzdb2,Kzdb3,Kzdb4,m,n),i、j=1,2,…,18——刚度矩阵元素(由隔振器垂向刚度系数和n,m确定),
Kzdai,Kzdbj,i=1,2,…,7,j=1,2,…,4,为机组各隔振器的垂向刚度系数;
Ci,j=C(Czda1,Czda2,Czda3,Czda5,Czda6,Czda7,Czdb1,Czdb2,Czdb3,Czdb4,m,n),
i、j=1,2,…,18——阻尼矩阵元素(由隔振器垂向阻尼系数和n,m确定);
Czdai,Czdbj,i=1,2,…,7,j=1,2,…,4,为机组各隔振器的垂向阻尼系数;
P——载荷向量(主要由机组的扭转力矩和倾覆力矩构成);
n、m——分别表示隔振器刚度的横垂比和纵垂比。
动力包的主要物理参数见表1。
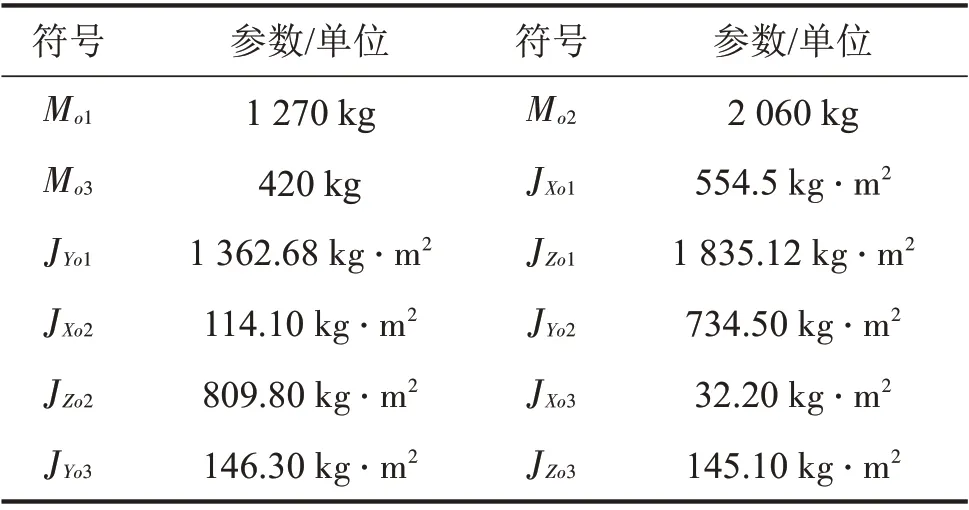
表1 动力包主要部件物理参数
依据ISO8528-9-2017.9 测点建议,在动力包机组上选取7个考核点1~7。设这些点的振动位移和速度分别为(Xi,Yi,Zi)和(Vix,Viy,Xiz),i=1,2,…,7,有:
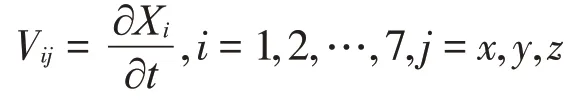
将Vij代入下列振动烈度表达式,即可得到动力包机组的振动烈度:
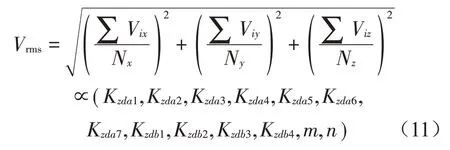
式中:∑Vix、∑Viy、∑Viz——各测点均方根速度和;Nx、Ny、Nz——X,Y,Z方向测点数。
2.2 机组振动烈度关于悬挂参数灵敏度计算方法
依据机组振动烈度函数及Sobol 灵敏度基本原理,得到机组振动烈度关于悬挂参数的灵敏度计算方法如下:
(1)建立随参数变化的振动烈度函数,将其作为灵敏度分析的目标函数,则振动烈度函数表达式为:

(2)在参数变化范围内对全部变量进行两次独立随机采样,采样点数为1 000,然后用蒙特卡洛法求解多重积分,如下:
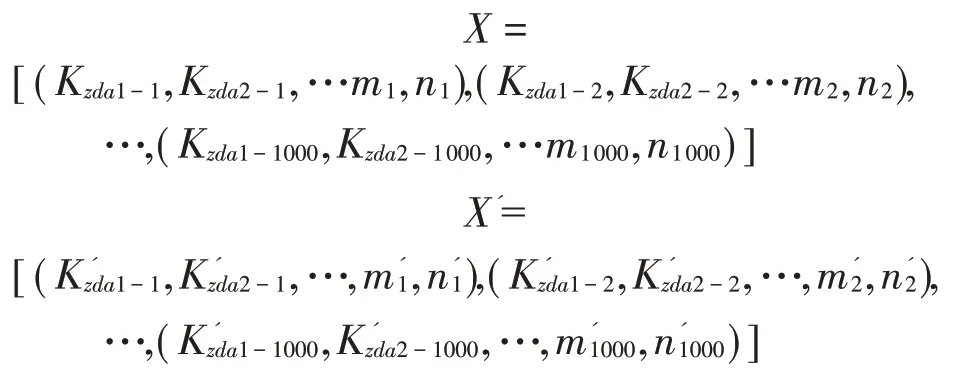
(3)求解机组振动烈度关于参数Kzda1的灵敏度时,设Kzda1的补集为z={ }Kzda2,Kzda3,…m,n,可分别获得振动烈度总方差Dv、偏方差Dvy以及振动烈度关于z的偏方差Dvz。
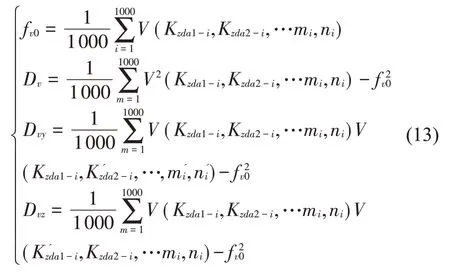
(4)将上述求得的Dv,Dvy及Dvz代入下式即可求出机组振动烈度关于悬挂参数Kzda1的1阶灵敏度Svy及高阶灵敏度。其它参数的灵敏度可通过相同方法得到。
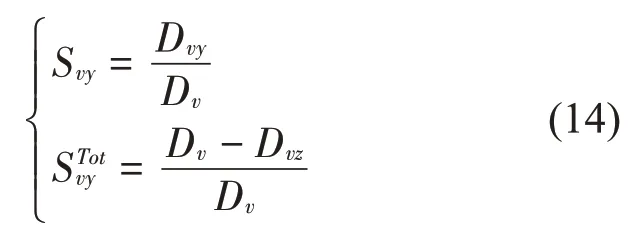
机组振动烈度关于悬挂参数的1阶灵敏度反映了参数变量单独变化对内燃动力包机组振动烈度的影响程度,总灵敏度不仅反映了该参数单独变化的影响,也反映了该参数与其它所有参数的交互作用对内燃动力包机组振动烈度的影响,在评价参数重要性上总灵敏度比1 阶灵敏度更可靠。当1 阶灵敏度与高阶灵敏度相差越大时,则说明此参数与其他参数交互作用影响越明显。
3 机组振动烈度关于悬挂参数灵敏度
将相关参数代入式(14)中,得到机组在各种转速工况下的灵敏度值如表2所示。

表2 机组振动烈度关于悬挂参数的灵敏度/*100
将计算结果绘制成灵敏度关于悬挂参数和机组转速的关系图如图2至图5所示。(为图示方便,参数Kzdai用Kai表示,参数Kzdbi用Kbi表示)。图2 和图3 为振动烈度关于悬挂参数1阶灵敏度,图4和图5为振动烈度关于悬挂参数的高阶灵敏度。
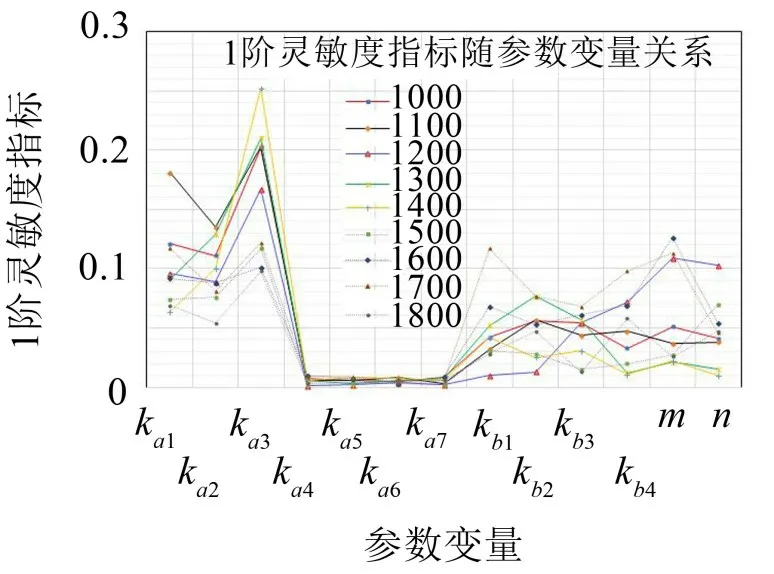
图2 机组振动烈度关于悬挂参数1阶灵敏度分布
由图2和图3可以看出,
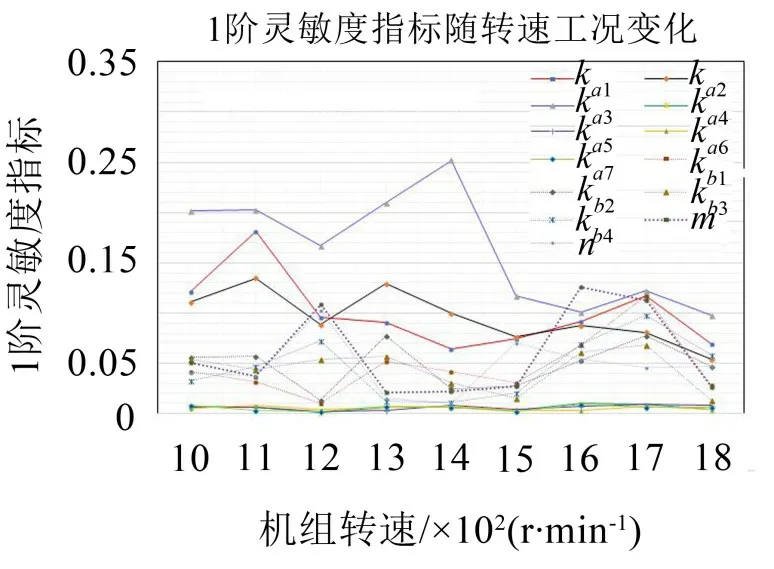
图3 1阶灵敏度随机组转速变化趋势
(1)机组振动烈度关于Kzda3的1 阶灵敏度高于其它参数。
(2)不同转速工况条件下机组振动烈度灵敏度有显著差异。
(3)相同转速条件下,不同悬挂对机组振动烈度灵敏度影响差异明显。
(4)振动烈度关于Kzda4、Kzda5和Kzda6的灵敏度小其它参数。
从图4和图5可以看出:

图4 机组振动烈度关于悬挂参数高阶灵敏度分布

图5 高阶灵敏度随机组转速变化趋势
(1)机组振动烈度关于Kzda3的高阶灵敏度大于其它参数。
(2)不同转速工况条件下机组振动烈度灵敏度有显著差异。
(3)相同转速条件下,不同悬挂对机组振动烈度灵敏度影响差异明显。
(4)振动烈度关于Kzda4、Kzda5和Kzda6的灵敏度小其它参数。
(5)当动力包转速工况为1 700 负载时,m的1阶灵敏度比n大,而m的高阶灵敏度比n小。由于1阶灵敏度未计入其它参数的影响,不能完全反映对参数的依赖程度,有可能导致1 阶灵敏度结果不能准确评价出参数的灵敏度,因此机组振动烈度对n的敏感程度高于m。
(6)从整体上看,对动力包机组振动烈度影响较大的参数为Kzda1、Kzda2和Kzda3。
4 结语
(1)建立了基于Sobol 法的动力包系统悬挂参数灵敏度分析方法,机组振动烈度关于Kzda3的高阶灵敏度大于其它参数、而关于Kzda4、Kzda5和Kzda6的灵敏度小其它参数。
(2)不同转速工况和不同悬挂参数条件下机组振动烈度灵敏度均有显著差异。
(3)当动力包转速工况为1 700时比值m和n的1 阶和高阶灵敏度变化较大。m的1 阶灵敏度比n大,而m的高阶灵敏度比n小,机组振动烈度对n的敏感程度高于m。
