非均布汽车冷却风扇噪声实验及数值研究
2021-10-22罗来彬吴亚东彭志刚欧阳华
罗来彬,吴亚东,2,彭志刚,3,欧阳华,2
(1.上海交通大学 机械与动力工程学院, 上海200240;2.燃气轮机与民用航空发动机教育部工程研究中心,上海200240;3.上海博泽电机有限公司,上海201801)
汽车风扇是汽车发动机冷却系统的重要组成部分,对充分发挥发动机的性能和延长其使用寿命至关重要。随着人们生活水平的不断提高,对汽车产生的噪声要求越来越严格。发动机是汽车主要噪声源之一,而发动机主要的噪声源是汽车冷却风扇[1]。因此如何快速、有效地预测汽车风扇产生的噪声,从而指导汽车的降噪设计是一个亟待解决的问题。
汽车风扇产生的噪声从频谱上看,主要分为离散噪声与宽频噪声。宽频噪声主要是由叶片表面的湍流边界层和尾缘涡脱落以及来流的不均匀性产生[2]。离散噪声主要是由动叶运动的压力场和气动干涉引起的叶片脉动力变化所产生[3]。文献[4-5]在不考虑换热器的影响下,对单独的汽车冷却风扇进行了研究,在CFD 计算的基础上,采用半经验公式计算风扇宽频噪声。此外,文献[6-7]通过提取均匀来流下,CFD计算的叶片表面力,利用移动点力模型计算离散噪声。但是,实际工作环境下,换热器对汽车风扇的影响不可忽略。而且,随着汽车风扇的不断发展,单独针对汽车风扇的离散噪声或宽频噪声的预测模型,不能很好地反映出实际情况。近年来,文献[8-10]考虑了换热器对汽车风扇噪声的影响,将换热器作为多孔介质模型,通过LBM方法结合声类比理论对汽车风扇噪声进行预测,然而,采用该方法计算噪声是基于LBM非稳态计算结果,需要耗费大量计算资源和时间。此外,以往针对汽车风扇的研究,其叶片大多是均布排列的,针对叶片非均布排列的风扇研究较少,文献[11]建立了叶片力和非均布角度之间的叶片力模型,并采用Lowson模型预测离散噪声,验证了模型的有效性,但是没有考虑换热器的影响。
本文根据汽车风扇噪声的特点,在实验和仿真过程中考虑换热器的影响,在噪声测试和气动实验的基础上,结合CFD 仿真,提出一种汽车风扇总噪声的预测模型,用于工程中在风扇设计初期对其噪声的快速预估。
1 研究对象和研究方法
1.1 研究对象
本文的研究对象是非均布7 扇叶(Uneven7)和非均布9 扇叶风扇(Uneven9),其中7 扇叶为主要的研究对象,9扇叶风扇作为验证噪声计算的对象。电机通过固定在风扇罩壳上带动风扇旋转,其中风扇罩壳上具有8 个非均布排列的支撑,并且各个支撑的大小存在差异。风扇罩壳为方形,由于受风扇实际安装位置下游的装置的影响,风扇通风区域不在方形中心。汽车风扇实物图如图1(a)所示。换热器(Regular condenser and radiator,RCR)实物图如图1(b)所示,换热器位于风扇上游,可与风扇罩壳装配。
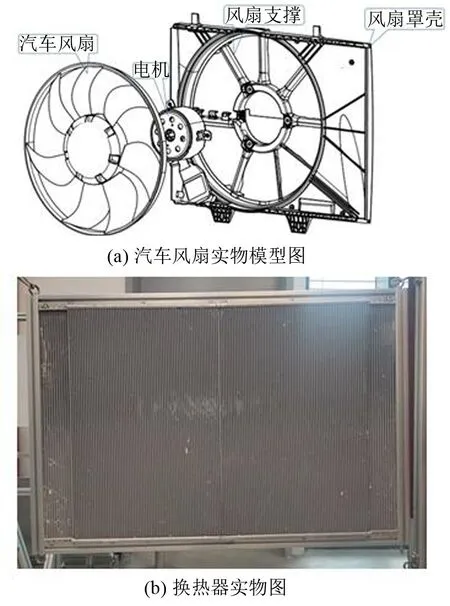
图1 汽车风扇实物模型图
风扇L 形叶冠到罩壳的距离(叶顶间隙)为5 mm。风扇支撑沿径向倾斜分布,风扇到支撑的最大距离为14.5 mm,最小距离为12.5 mm。风扇具体的设计参数如表1所示。

表1 汽车风扇设计参数
1.2 试验方法和设置
(1)声学试验设置
本文噪声测试标准参考国标《GB/T 2888-2008风机和罗茨鼓风机噪声测量方法》,测试装置图如图2 所示。风扇中心和麦克风距离地面的高度均为1 m,麦克风位于风扇上游1 m处。测试采用的麦克风型号为PCB HT378B02,其中设置采样频率为32 768 Hz,采样时间为30 s。
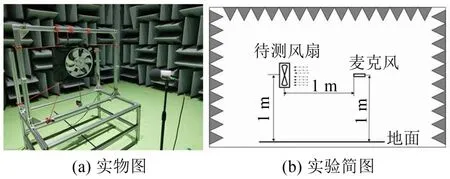
图2 噪声测试示意图
(2)气动试验设置
为了给CFD仿真计算提供依据同时验证仿真结果,对汽车风扇进行了气动性能实验。气动实验的风洞如图3所示。风洞实验的标准参照ISO5801,风洞矩形腔体的尺寸为6.50 m×2.51m×3.12 m,可测流量范围为0.01m3/s~6.8 m3/s,可测压力范围为-3 kPa~3 kPa,压力测量误差小于5 %,流量测量误差小于1%。

图3 实验风洞示意图
(3)热线试验设置
采用热线测试了风扇转速为2 900 r/min,给定进口流量下,不同风扇加换热器前后风扇支撑出口速度变化情况。测试过程中将风扇固定在图3中的风洞出口,热线测量平面位于风扇支撑下游120 mm,将热线固定在坐标架上,如图4所示,通过移动坐标架在半径为200 mm的圆形平面内的每相隔45°的半径上相距20 mm 取一个测点,在测量平面内共有81 个测点,平面和测点位置如图5 所示。热线测试采用DANTEC 公司热线测量系统。本文测试采用的是55P11型直丝探针。测试过程中设置采样频率10 kHz,采样时间为1 s。

图4 热线测试装置图
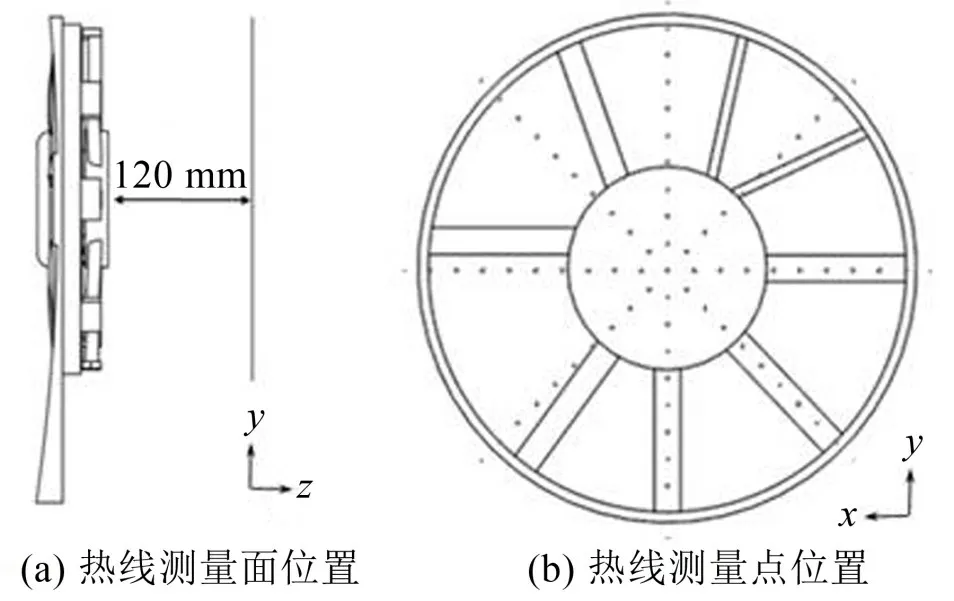
图5 热线测量示意图
1.3 CFD仿真设置
风扇仿真流域主要分为4 个部分,如图6 所示。分别是矩形进口域,风扇旋转域,风扇支撑域(其中包含风扇罩壳)和风扇半球形出口域。位于风扇上游的换热器简化为CFX中的多孔介质模型,即将换热器视为一个多孔介质域,由实验测得的换热器压阻特性曲线得到CFX 模型中所需的孔隙率和损失系数等参数。进口域的长度为风扇直径的4 倍,横截面长、宽分别约为风扇直径的3.2 倍;出口域半球直径为5.1倍风扇直径。进口域和出口域尺寸较大,使得气流能在流域内充分发展。

图6 风扇仿真流域模型图
求解器采用Ansys-CFX®,求解器的设置为:湍流模型采用kω-SST 模型,设定风扇转速,进口给定实验测量的质量流量,出口采用Opening边界条件,给定出口静压。通过改变进口流量的大小,计算风扇的压升。
2 声学和气动性能
2.1 声学性能
实验测得的汽车风扇在2 900 r/min下采用A计权得到的频谱图如图7所示。图中RCR表示冷却模块的标准换热器。以非均布7扇叶风扇为例说明噪声测试结果,从图中可以看到,采用叶片非均布排列方式的汽车风扇叶片通过频率(Blade passing frequency,BPF)处声压级为68.3 dB(A),除BPF声压级较大外,其他各阶谐波处也具有明显的声压级,这与均布叶片的风扇除BPF 及其倍频处的声压级外,其他各阶谐波处的声压级较小的现象具有明显的差异。同时,随着离散噪声向各阶谐波分散,使得离散噪声和宽频噪声的差值减小。

图7 非均布7扇叶频谱图
从频谱图上还可以看到,在200 Hz 以下时,存在多个窄带谱,这主要是由于叶顶间隙处的泄漏流造成的[12]。频率在1 000 Hz 以下时,加换热器后的宽频噪声增加,1 000 Hz以上时,加换热器后的离散噪声更加明显。从7 扇叶的频谱图上看,加换热器会显著降低5次谐波频率处的离散噪声。
图8给出了实验测得的A计权下,2 900 r/min总声压级的情况,从中可以看到,加换热器后对总噪声的影响较小,但会减小宽频噪声,7扇叶加换热器后离散噪声增加,9扇叶加换热器后离散噪声降低,总噪声的变化主要与加换热器后增加的宽频噪声和减小的离散噪声的相对值有关。

图8 不同风扇噪声对比
通过实验测试了不同转速下的声压级变化情况,如图9所示。从图中可以看到,风扇的声压级近似与转速的6次方成正比。这符合典型的偶极子声源的特征。不加换热器时的幂次大于加换热器后的幂次。
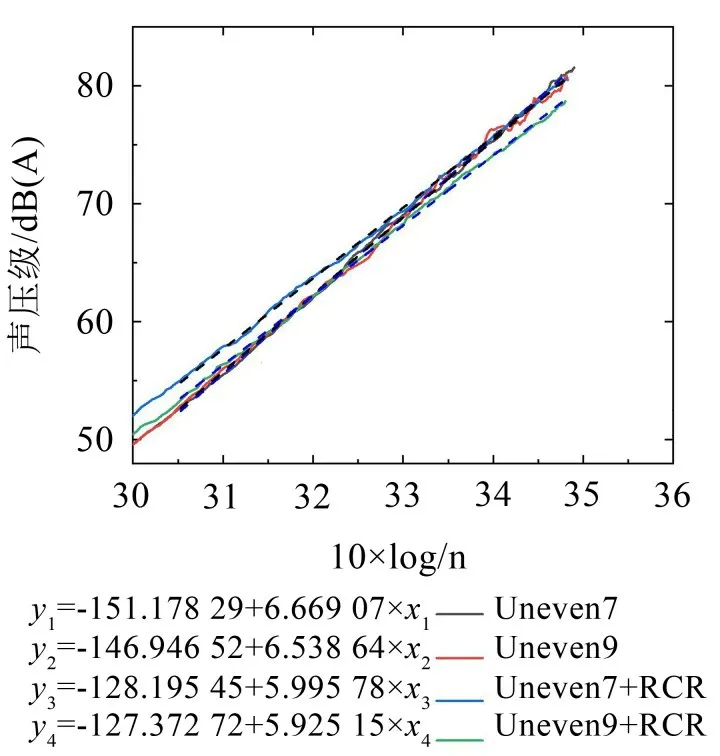
图9 声压级与转速关系图
2.2 气动性能
首先,对比了风扇CFD计算和实验测得的性能曲线如图10 所示。从图中可以看到CFD 仿真计算结果与实验所得性能曲线吻合较好。

图10 CFD仿真与实验特性曲线对比图
为了验证仿真模型的计算结果的准确性,将仿真结果与热线的测试结果进行对比。仿真计算的风扇支撑下游与热线测点相同位置的速度与热线测试结果的对比如图11 所示。其中横坐标为热线测点编号,其编号规则为:如图5(b)以测量面中心为原点,编号为0,从x轴正向开始,沿径向依次编号为1~10,再顺时针旋转45°,沿径向编号为11~20,之后依次顺时针旋转45°至整个测量面,共81 个测点编号。从图11 中的仿真和热线测试结果的对比来看,存在仿真结果和热线结果相差较大的测点位置,但是大多数测点的仿真结果和实验吻合较好,并且仿真和实验所得平均速度相差在0.5 m/s以内(误差在5%以内),因此,可以认为仿真得到的各点的速度与实验结果在整体上是一致的,只是在某些局部位置上存在差异,而这些局部位置对总噪声的影响较小。
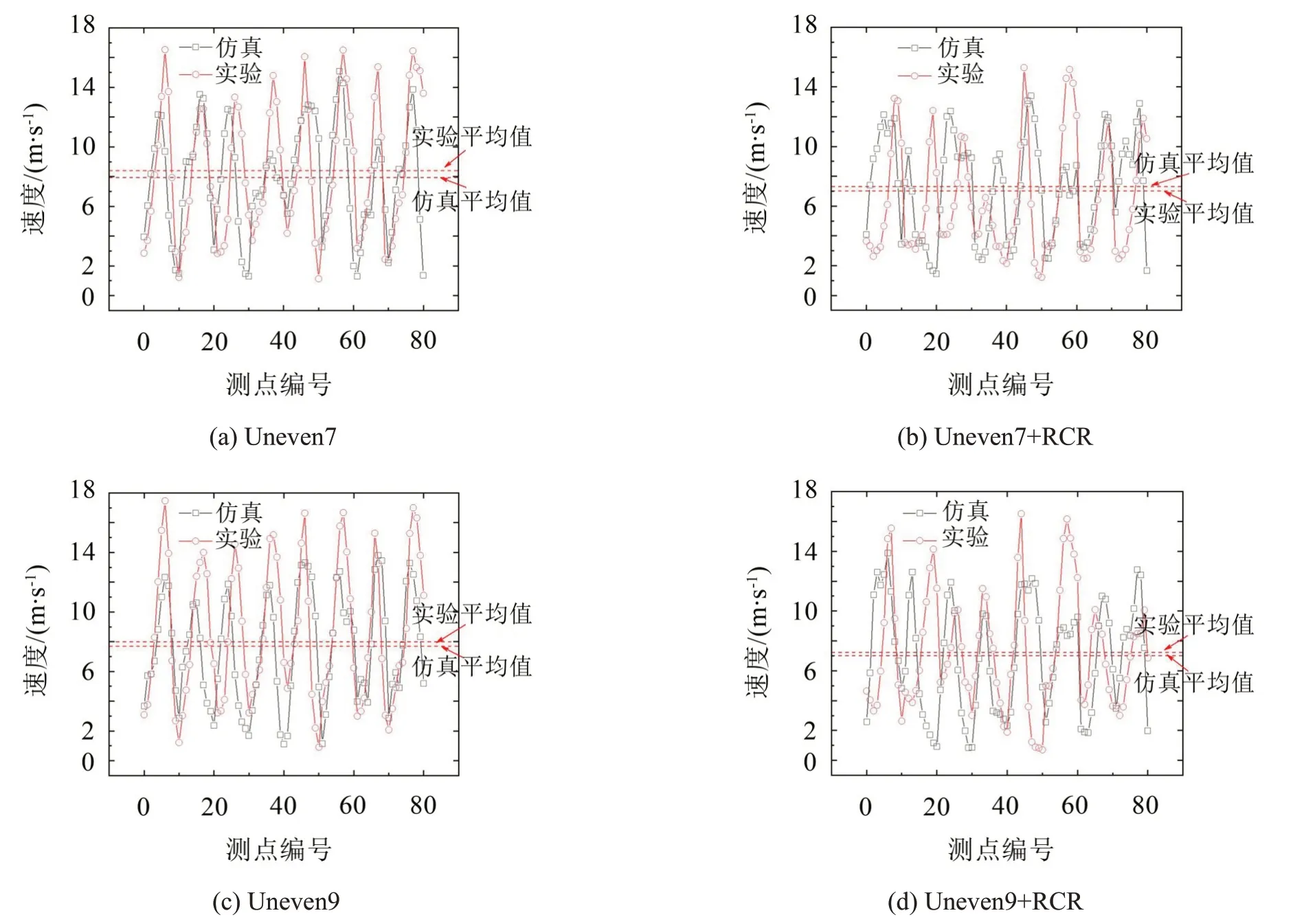
图11 仿真和热线速度对比图
2.3 涡声源分布
Powell[13]提出气动噪声主要来源于涡的拉伸和破裂,对于等熵流动,可以用涡量和速度叉乘的散度表示声源的大小。图12 所示为在CFD 计算的基础上,提取的非均布7扇叶风扇叶片表面的声源分布,从图12(a)中可以看出,声源主要集中在叶片压力面和吸力面靠近前缘的叶中部分,此外,叶片尾缘也是一个重要的声源区,图12(b)为风扇叶片压力面声源分布,为了详细看到尾缘声源分布,以1号风扇叶片为例,将其叶片表面声源分布放大如图12(c)所示,从图12(c)中可以看到叶片尾缘处的声源值也比较大。
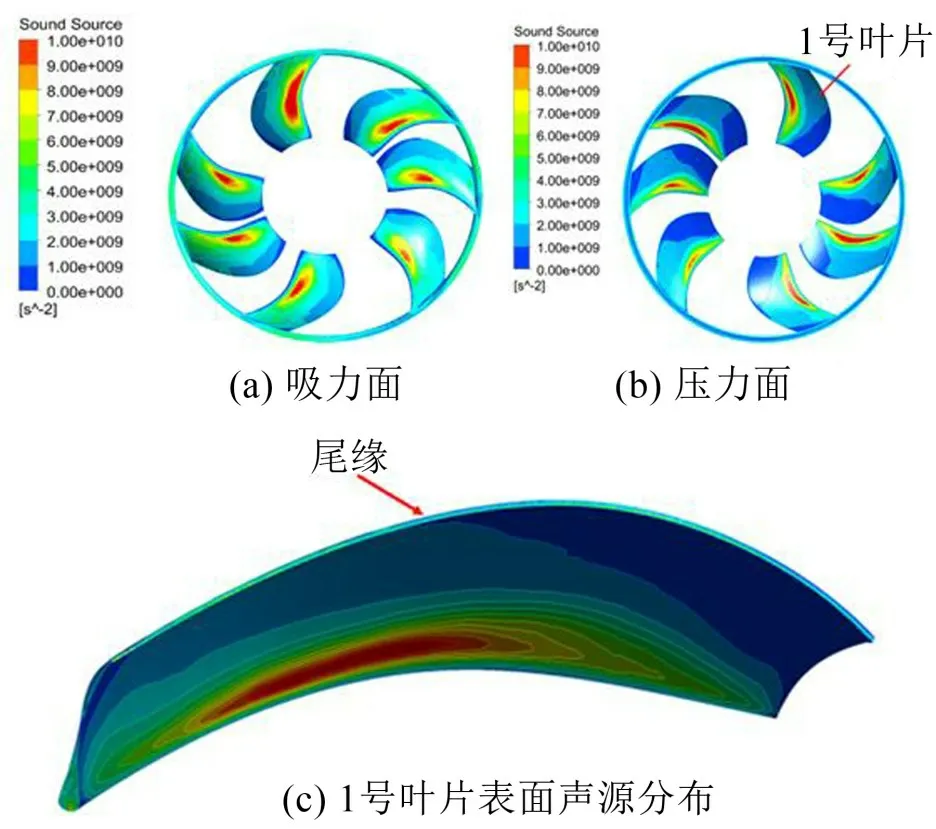
图12 风扇叶片表面声源分布
3 汽车风扇噪声预测模型
1969年Ffowcs 等[14]采用广义函数法并且考虑运动固体边界对声音的影响,提出了Ffowcs Williams-Hawkings 方程。确认运动物体与流场的相互作用产生的声场是由单极子、偶极子、四极子组成,其方程为:
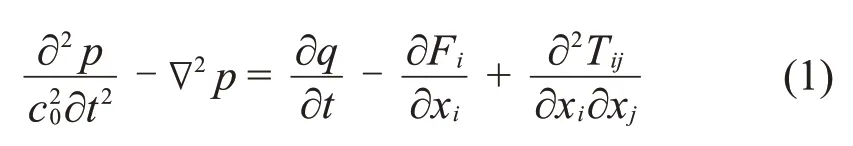
式中:co为声速;q为通过边界的质量流量,Fi为作用在边界上单位面积上的力矢量,Tij为Lighthill 应力张量。
低压轴流风扇的噪声类型主要是偶极子,忽略单极子和四极子的影响,偶极子声源的辐射声压可表示为:
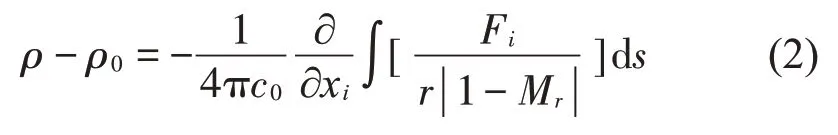
式中:Mr为瞬时对流马赫数,r为观察点到源点的距离;根据量纲分析[15]:

式中:U0为特征速度,L为特征长度。由此可以得到声强与速度的关系为:

从式(4)可以看出偶极子源产生的声强近似和特征速度的6 次方成正比,由声强和声压级的关系可得偶极子源产生的声压级为:

式中:C为与特征长度和声源距离相关的常数,Pa=20×10-6Pa 参考声压,α为动能转换为声能的转换系数。
由汽车风扇的噪声源特性以及在此基础上结合风扇表面的声源分布,声源主要位于与叶片靠近前缘或尾缘部分分别相切的前缘面和尾缘面,风扇产生的声压级可表示为:

其中:U1、U2分别为前缘面和尾缘面的特征速度。
3.1 确定特征速度和转换系数
(1)特征速度
位于风扇叶片上游的罩壳和下游的支撑以及叶冠都会对经过风扇的流场产生影响,使得很难借助理论分析得到速度分布。此外,风扇罩壳和支撑给直接测量风扇前缘和尾缘速度分布造成了很大困难。因此,为了获得较为准确的前缘和尾缘速度分布,本文通过CFD仿真获得相对速度。
前缘面和尾缘面的相对速度计算公式如下:
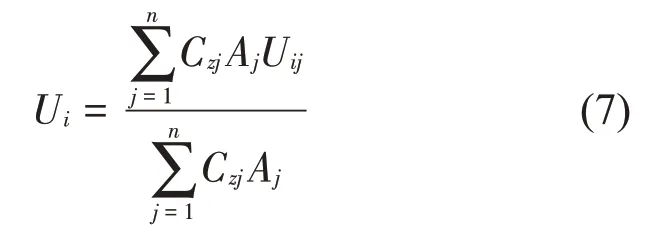
式中:i=1,2,分别代表前缘面、尾缘面相对速度;n为面上网格单元总数;Czj为面单元绝对速度轴向分量;Aj为单元面积;Uij为相对速度。
(2)转换系数
通过计算不同转速下的相对速度带入声压级预测模型,和实验值进行比较,使误差的平方和(SSE)达到最小确定α1和α2。其中SSE的计算方式为:

式中:k为仿真计算选取的不同转速个数。
3.2 验证噪声计算模型
通过非均布7扇叶的仿真结果和噪声测试结果利用上述噪声计算公式得到α1和α2的值为0.000 3,如图13(a)所示为不同转速下,非均布7 扇叶风扇预测模型计算的噪声和实验值的对比。可以看到选用此α1和α2的值具有较好的预测精度。
在不改变α1和α2的条件下,分别将该预测模型用于7扇叶加换热器(RCR)、9扇叶、9扇叶加换热器(RCR)的噪声仿真。该模型的预测值和实验值的对比如图13(b)、图13(c)、图13(d)所示,从图中可以看出预测值和实验值相差1.5 dB(A)以内。说明可以用该预测模型预测不同转速下,汽车风扇以及汽车风扇加换热器所产生的噪声。
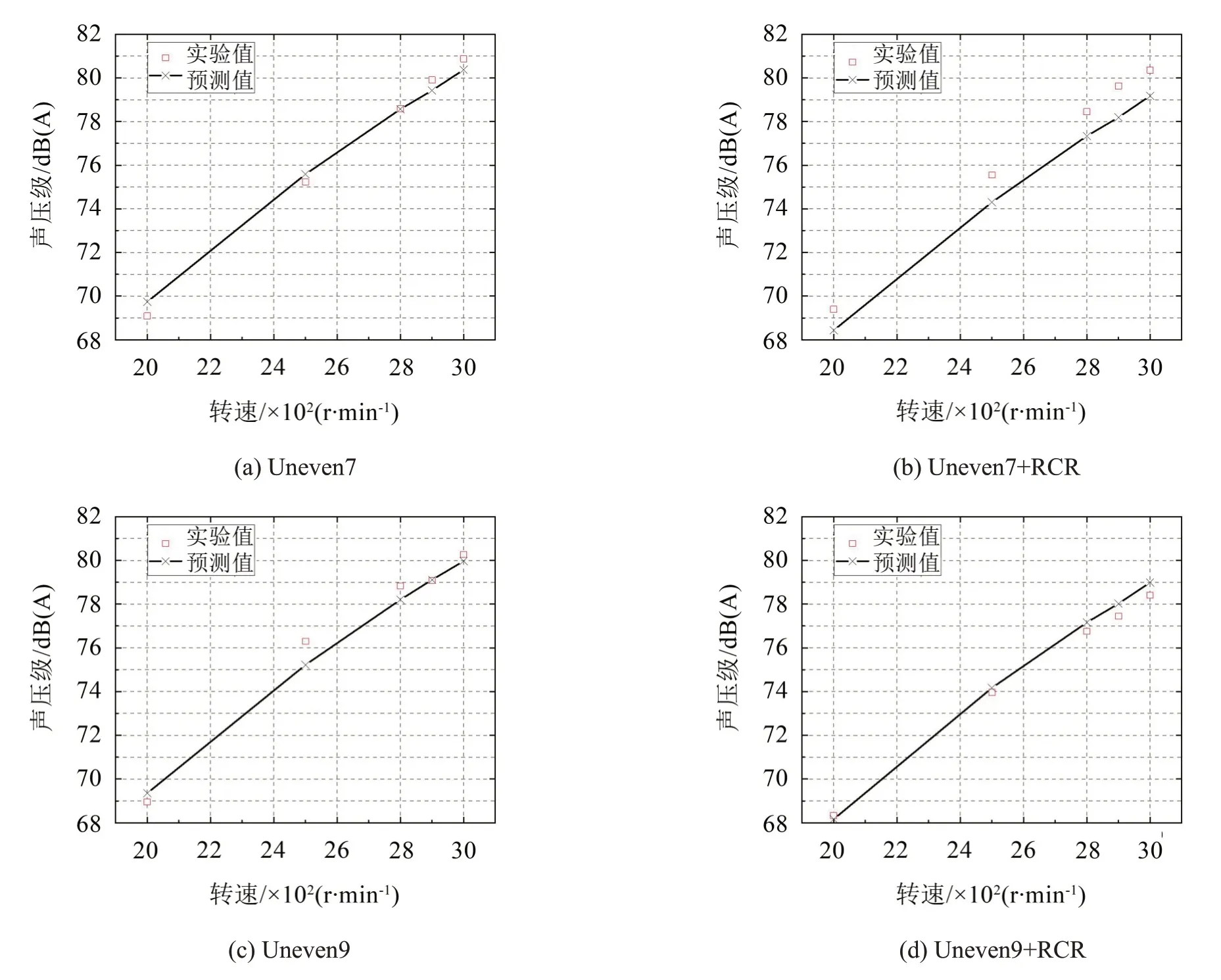
图13 噪声预测值与实验值对比
4 结语
本文通过对汽车风扇进行声学和气动性能测试,在仿真计算的基础上结合噪声测试结果,得到了风扇噪声的预测模型。主要结论如下:
(1)非均布汽车风扇加换热器前后,其声压级近似与转速的6 次方成正比,符合典型的偶极子声源的特性。风扇相同转速下,加换热器后会使风扇模块产生的宽频噪声增加,但对总噪声的影响较小。
(2)基于CFD 计算结果,利用涡声理论计算叶片的声源分布,结果表明:汽车风扇叶片表面的声源主要位于叶片压力面和吸力面靠近前缘的叶中部分以及叶片尾缘。
(3)基于风扇的主要声源为偶极子,声压级与速度的六次方成正比的假设,通过仿真和实验结果得到的预测模型可有效预测汽车风扇产生的噪声,也可以用于加换热器后的汽车风扇模块的噪声预测,并且具有一定的通用性。
