基于敏感特征评估的退火窑辊道轴承故障诊断方法

周康渠，阚志群，辛 玉，吴雪明，张朝武

（1.重庆理工大学 机械工程学院，重庆400054；2.重庆万盛浮法玻璃有限公司，重庆400800）

退火窑辊道是承载、拉引玻璃产品的关键部件，一旦出现轴承故障将使辊道丧失运转平稳性，对玻璃品质造成重大影响，甚至导致整条生产线停产，给企业造成巨大的经济损失。因此，如何高效准确地诊断出辊道轴承的故障状态，对提高辊道运行平稳性和可靠性具有重要意义。

退火窑辊道轴承在恶劣环境中持续运转，有效的故障振动信号不可避免地被机械设备的强背景噪声淹没，这将加大有效特征提取难度并降低诊断精度，进而影响诊断结果。因此，滤除轴承振动信号中的噪声，提高采集数据的有效性和准确性，是精确诊断故障的基础。传统的降噪方法主要有EMD降噪、小波阈值降噪等。EMD 降噪方法是通过将信号分解后的高频IMF 分量直接滤除，对剩余分量进行重构实现降噪，可能会导致降噪后信号失真。小波阈值降噪方法由于小波基函数、分解层数及阈值的选择存在一定的困难，导致其降噪效果不理想。针对EMD降噪和小波阈值降噪方法存在的不足，通过将两种降噪方法相结合，利用连续均方误差准则[1]和相关系数[2]等算法筛选含噪较多的IMF 分量，并对其进行小波阈值降噪。

针对滚动轴承故障诊断中的特征信息提取，通常利用小波包分解[3]、经验模态分解[4]等时频分析方法对非平稳振动信号进行分解，然后从分量信号中提取能量特征[5]、样本熵特征[6-8]、多尺度熵[9-10]、近似熵[11]等特征信息。由于提取的特征多样，导致特征集维度过高，而一些不敏感特征会增加计算额外负担，甚至降低故障诊断精度。因此，有必要对众多特征进行评估，剔除不相关特征和冗余特征，筛选出敏感特征，组成识别度高的敏感特征集，提高滚动轴承故障诊断的效率和准确性。针对特征选择，徐国权[12]等提出基于故障类内、类间标准差的多特征评估筛选方法。柏林等[13]基于单调性与敏感性定义了性能退化跟踪能力对轴承特征进行量化评估，筛选出表征轴承性能退化的多维特征集，并采用相似近邻传播聚类算法对多维特征集进行聚类和筛选。

针对退火窑辊道轴承振动信号存在强噪声干扰和故障诊断效率及准确率低等问题，本文将灰关联熵分析法引入信号降噪，用于筛选和判断原信号经EMD分解后各IMF分量的属性，对与原信号灰关联熵值小的IMF 分量进行小波阈值降噪，重构得到降噪信号。然后，对降噪后信号进行小波包分解，提取分量信号的时域和频域特征，计算故障特征类间、类内距离的敏感特征评估因子，对全特征集进行敏感度评估，筛选出敏感特征组成优化特征集。最后，利用RBF 神经网络[14]进行故障识别。实验结果表明，该降噪方法性能优越，特征评估方法能够有效筛选敏感特征，提升故障识别效率及诊断准确率。

1 数据预处理与特征提取

1.1 基于灰关联熵分析的信号降噪方法

针对滚动轴承故障信号中的强背景噪声干扰，传统上，通常采用EMD或者小波阈值方法降噪。但是，上述两种降噪方法通常会导致信号失真严重。由于噪声主导分量与原信号之间的灰熵关联度相对较小，而有用信号主导分量与原信号之间的灰熵关联度相对较大，考虑将EMD和小波阈值的优点相结合，利用EMD 将原始信号分解为若干个IMF 分量，通过设定灰关联熵值来筛选和判断各IMF分量的属性。采用灰关联熵分析法筛选噪声主导分量，利用小波阈值法对噪声主导分量进行降噪处理，最后将降噪后分量与其余分量重构得到有效故障特征信号。改进的降噪方法具体流程如图1所示。

图1 基于灰关联熵分析的振动信号降噪流程

(1) 设轴承故障振动信号为S0(t)，对其进行EMD 分解，得到m个IMF 分量hi(t)和一个残余分量。

(2)根据式(1)分别计算原始信号与各IMF 分量在第k个数据点的灰关联系数：

式中：ξ表示分辨系数，取值为0.5。

求解各灰关联系数的状态概率：

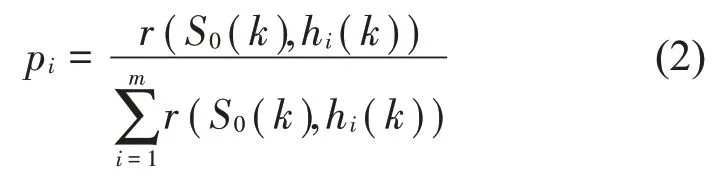
求解灰关联熵：

(3)根据步骤(2)计算各个IMF 分量的灰关联熵值，并选取灰关联熵值最小的q个分量作为噪声主导分量，对其进行小波软阈值降噪，小波分解层数为1，小波基函数为coif2，软阈值公式为：

(4)将降噪后分量与其余分量进行信号重构，得到最终降噪信号。

1.2 特征提取

轴承振动信号的特征参数可表征其故障信息，通过提取轴承的故障特征，进而辨识故障类别。选取时域特征中对磨损类故障比较敏感的均方根特征，对脉冲冲击类故障比较敏感的峭度指标、峰值指标、波形指标、裕度指标、脉冲指标等无量纲特征，其特征值不受工况变化的影响，且具有良好的早期故障诊断能力。选取频域中能量熵、样本熵及频谱熵特征，可以有效反映信号频谱特征信息。将时域和频域特征结合，组成全特征集用于特征敏感度评估。

2 基于距离的敏感特征评估

提取敏感特征是正确诊断轴承故障的前提。由于不相关特征和冗余特征增加了样本容量，却未增加新的识别信息，导致整个特征集的识别有效性下降，识别效率降低。针对上述情况，提出基于故障类间、类内距离的特征评估方法，判断某一特征满足：对于同一故障类型的类内距离越小，对于不同故障类型的类间距离越大，则这一特征属于敏感特征。基于上述原则筛选出对故障类别更敏感的时域、频域特征，构成维数更小的特征集，提高分类器分类性能，精确诊断轴承故障。敏感特征评估流程如图2所示。

图2 敏感特征评估流程

定义并求解距离评估因子。设轴承特征样本集为{X1,X2,…,Xi,…,XN}，含有J种故障类型，其中Xi=[x1,x2,…,xL]T，N为样本数量，L为小波包分解后的频带个数，则对于第w个特征第j类故障的N个样本可建立矩阵：

定义并计算类间距离。首先对第j类故障第l频带所有样本的特征值取平均：

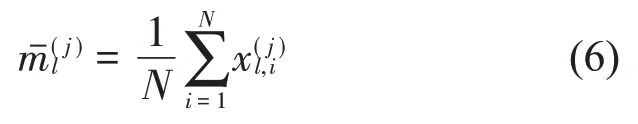
对L个频带的特征平均值取平均：

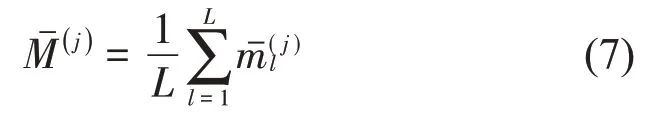
然后，对J类故障的特征平均值取平均：

则第w个特征的类间距平均值为：

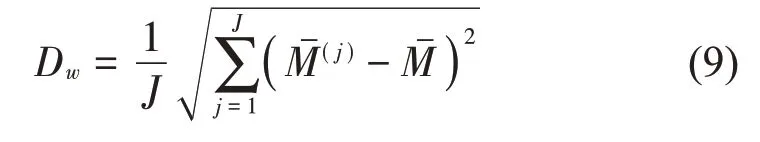
定义并计算类间离差：

定义并计算类内距离。首先计算第j类故障所有样本的类内平均距离：

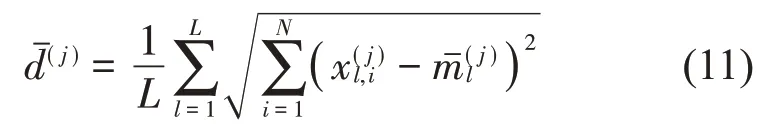
则第w个特征的J个类内距的平均值为：

定义并计算类内离差：

定义并计算权值：

定义并计算距离评估因子：

该距离评估因子为加权后类间距离与类内距离的比值，反映了第w个特征对J类故障进行区分的难易程度，aw值越大表示该特征越敏感，意味着区分轴承信号故障类型的能力越大。因此，根据各特征的距离评估因子aw的降序排列，可从全特征参数中选出敏感特征。

3 基于RBF神经网络的故障诊断

RBF 神经网络[14]是一种前馈神经网络，其结构简单、训练简洁且学习收敛速度快、能够逼近非线性函数，广泛应用于分类问题。定义网络拓扑结构如图3所示。

图3 网络拓扑结构

本文故障诊断流程定义如下：

(1)使用改进的降噪方法对轴承振动数据进行降噪预处理。

(2)对降噪信号进行小波包分解，提取1.2 节所述时域及频域共9个特征，组成全特征集。

(3)计算距离评估因子，筛选出适合该振动数据的最优特征组成敏感特征集。

(4)利用RBF 神经网络模型对敏感特征集进行识别，得出轴承故障诊断结果。图4 所示为故障诊断流程。

图4 故障诊断流程

4 实验结果及分析

4.1 滚动轴承故障诊断

首先以美国凯斯西储大学[15]（Case Western Reserve University，CWRU）轴承数据中心的内圈故障数据为例，利用信噪比（Signal-noise Ratio，SNR）和均方根误差（Root Mean Squared Error，RMSE）两个指标来衡量改进降噪方法与传统小波阈值法的降噪效果。轴承内圈时域波形如图5所示。

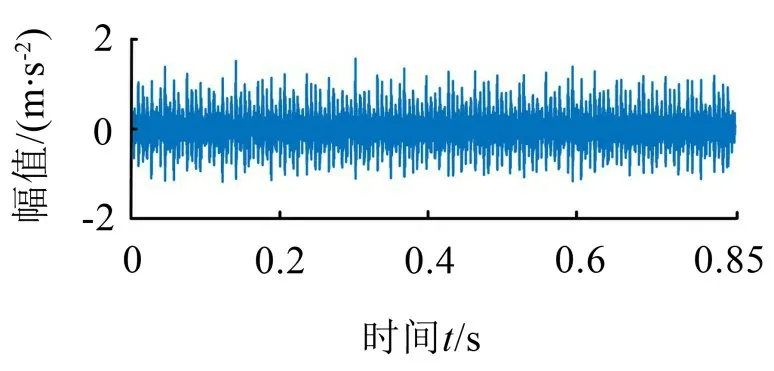
图5 轴承内圈故障信号时域波形

（1）利用改进降噪方法对该数据进行降噪。首先对其进行EMD 分解，得到12 个IMF 分量和一个残余分量，采用灰关联熵分析对IMF分量进行筛选，依据式（3）求出各个IMF 分量与原始信号之间的灰关联熵值，如表1所示。

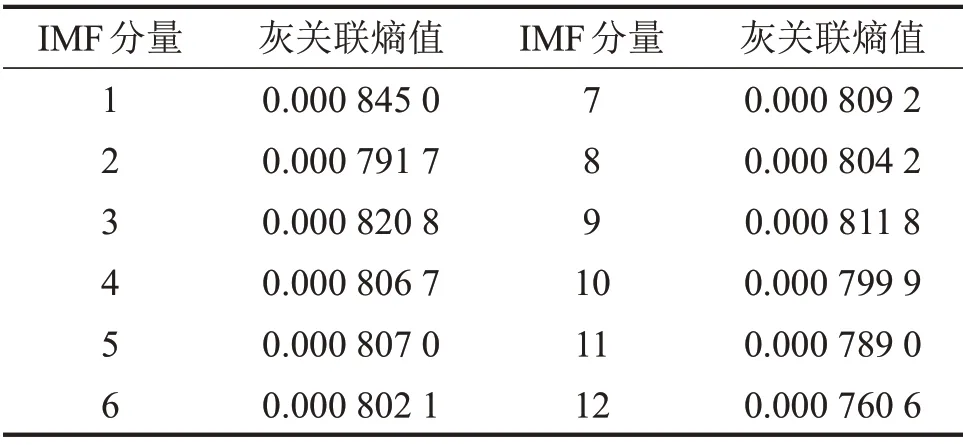
表1 各IMF分量与原始信号的灰关联熵值

根据表1 中的灰关联熵值，选取噪声主导分量并进行小波阈值降噪。依据实验结果，若选取IMF分量的个数多于3个，会导致整体降噪效果下降，若选取少于3 个分量则产生过降噪情况。因此，选取灰关联熵值最小的IMF2、IMF11、IMF12共3 个分量作为噪声分量并对其进行小波阈值降噪，将剩余分量与降噪后的分量进行信号重构，降噪后信号时域波形如图6所示。

图6 轴承内圈故障信号降噪后时域波形

改进降噪方法与传统小波阈值降噪效果如表2所示。

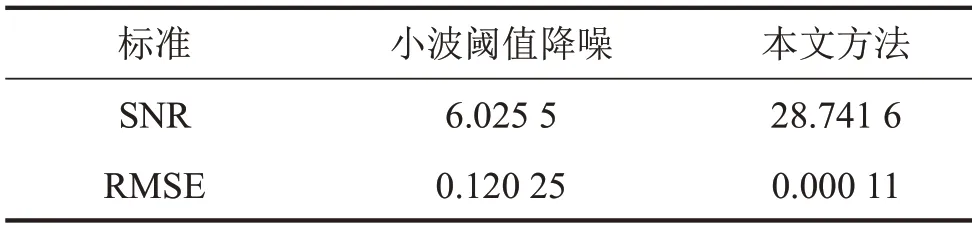
表2 两种降噪方法对比

对比表2 中两个指标的性能可以看出，本文所提方法降噪后的信噪比达到28.7，RMSE为0.000 1，明显优于采用小波阈值降噪后的信噪比。在保留信号完整性的基础上，充分提升了信噪比，降噪效果要明显优于传统小波阈值降噪，为后续精确诊断故障提供保障。

（2）对降噪处理后的轴承4类故障信号：轴承正常，外圈故障，内圈故障及滚动体故障，每类50组样本，共200个样本，进行小波包3层分解，将信号在全频带范围内进行多层次划分，对得到的8 个频带信号分别提取5 个无量纲指标和1 个有量纲指标及3个频域特征。

（3）筛选敏感特征：分别计算时域特征和频域特征参数的距离评估因子，得到特征敏感度排序如图7所示。

图7 特征的评估结果

由图7可知，时域特征的敏感度为均方根＞波形指标＞峭度指标＞裕度指标＞脉冲指标＞峰值指标；频域特征敏感度为样本熵＞频谱熵＞能量熵。为验证评估结果，将9个特征参数，4类故障，每类50个样本共200个样本绘制成特征分布图，如图8所示。

由图8 可见，对于4 类故障类型的分类问题，时域6 个特征的整体区分能力依次是均方根＞波形指标＞峭度指标＞裕度指标＞脉冲指标＞峰值指标。图8（b）的波形指标能够很容易的区分四类故障，但在类内距离上却高于均方根，因此整体区分能力弱于均方根。尽管图8（c）的峭度指标能够将第一、第二和第三类故障分开，但对于第二和第四类或者第三和第四类故障的区分能力较弱。图8（d）的裕度指标对于第三和第四类故障的区分能力较弱，且类内距离较大，导致该特征在同类样本内波动明显。图8（e）脉冲指标和图8（f）峰值指标几乎无法区分四类故障。频域3个特征对四类故障的整体区分能力依次是样本熵＞频谱熵＞能量熵。图8（h）频谱熵和图8（i）能量熵对于第二和第四类故障的区分能力较弱，且类内距离较大，导致该特征在同类样本内波动明显。分析表明，距离评估因子对时域6 个特征及频域3 个特征的敏感度评估与图8 中对应的实际特征分布情况相吻合。

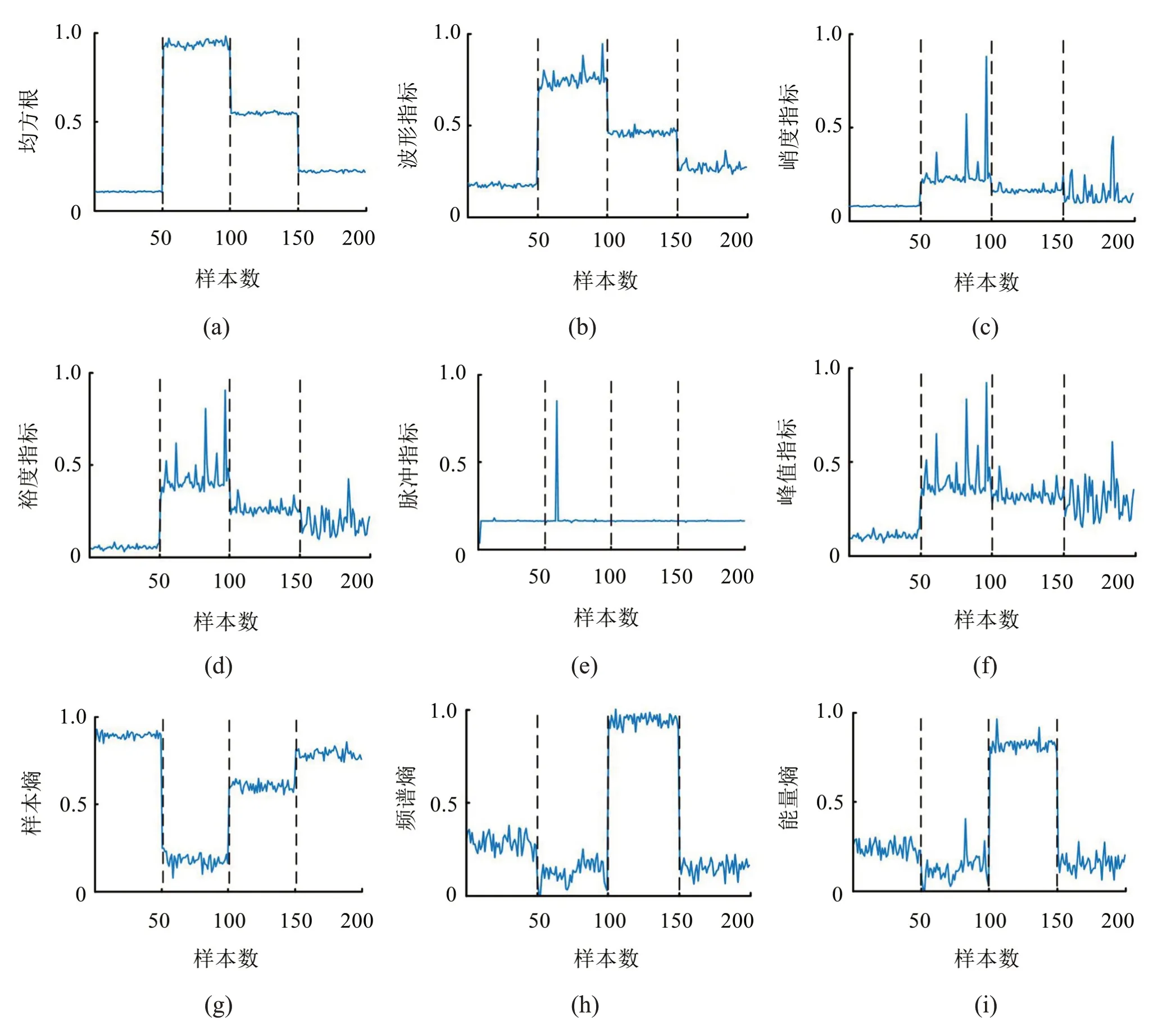
图8 特征分布

根据全特征参数的敏感度评估结果，选取时域中均方根和波形指标，频域中样本熵特征，组成24维故障特征向量，4类故障，每类50个样本共200个样本组成敏感特征集用于RBF 神经网络进行训练及故障识别。

（4）以24 维故障特征向量作为网络的输入，定义轴承无故障（1，0，0，0）、外圈故障（0，1，0，0）、内圈故障（0，0，1，0）和滚动体故障（0，0，0，1）作为输出，隐含层采用Gaussian函数作为径向基函数。为消除测试结果的随机性影响，将200 个样本随机分成训练样本和测试样本，测试20次神经网络对测试样本的识别准确率并取平均值。为验证该诊断模型的优越性，与2种传统轴承故障诊断模型作对比，传统轴承故障诊断方法对4类轴承故障信号作小波阈值降噪，分别提取小波包样本熵特征和EMD 能量特征，每类故障信号得到50 组样本，对得到的200 组样本随机分成训练样本和测试样本，测试20次RBF神经网络对测试样本的识别准确率并取平均值，测试结果如表3所示。

表3 诊断模型对比

由表3 可知，基于敏感特征评估的轴承故障诊断模型对轴承故障的识别准确率为100%，识别耗时2.03 s，两项指标均优于以上2种传统故障诊断模型，具有更优的识别准确率及识别效率。

以上分析结果表明，经距离评估因子筛选出的样本熵、均方根及波形指标组成的敏感特征集，特征维度较小、识别有效性高，RBF 神经网络模型的训练、识别效率及识别准确率较高。该轴承故障诊断模型具有一定的优越性。

4.2 退火窑辊道轴承故障诊断

为进一步验证本文方法对实际工况下轴承故障诊断的有效性，对玻璃生产线退火窑主传动系统辊道轴承进行了现场测试。该辊道轴承在低速工况下连续运转，图9 为实验装置结构示意图。由于玻璃生产线不可停机，无法拆机验明轴承故障类型，因此将采集的辊道轴承振动信号分为轴承正常、轴承故障2种类型。辊道所用轴承型号为SKF-1218K双列调心球轴承，轴承转速为14 r/min，测点设置为轴承座正上方，采样频率为10 240 Hz，利用振动加速度传感器采集轴承故障振动信号。

图9 退火窑主传动系统示意图

该主传动系统由同步电动机、二级减速器和超越离合器组成，动力经通轴及齿轮传递给各辊道。辊道通过轴承座悬挂在横梁上，配合调心球轴承保证其平稳转动，图10 所示为编号176 号辊道轴承振动数据采集现场。

图10 辊道轴承数据采集现场

辊道轴承正常信号与故障信号的时域波形如图11 所示，可见176 号辊道轴承振动信号相较于正常信号，其幅值成倍增长，并伴有明显的周期性冲击成分。

图11 两种故障类型的信号时域波形

第一步，对176 号辊道轴承振动信号进行降噪预处理：经EMD 分解得到12 个IMF 分量和一个残余分量，前6个分量如图12所示。

图12 IMF分量

采用灰关联熵分析对IMF 分量进行筛选，计算各个IMF 分量与原始信号之间的灰关联熵值，如表4所示。

表4 灰关联熵值

选出灰关联熵值最小的3 个分量：IMF1、IMF3、IMF12作为噪声分量并对其进行小波阈值降噪，将剩余分量与降噪后的分量进行信号重构。降噪后信号时域波形如图13所示。计算其信噪比达到16.41。

图13 降噪后故障信号

第二步，对降噪处理后的2类轴承振动信号：轴承正常及轴承故障，每类110 组样本，进行小波包3层分解，提取时域5个无量纲指标和1个有量纲指标及3个频域特征。图14所示为轴承故障信号的各频带重构结果。

图14 小波包重构结果

第三步，分别计算时域特征和频域特征参数的距离评估因子并筛选敏感特征组成优化特征集。各特征的评估因子计算结果如表5所示。

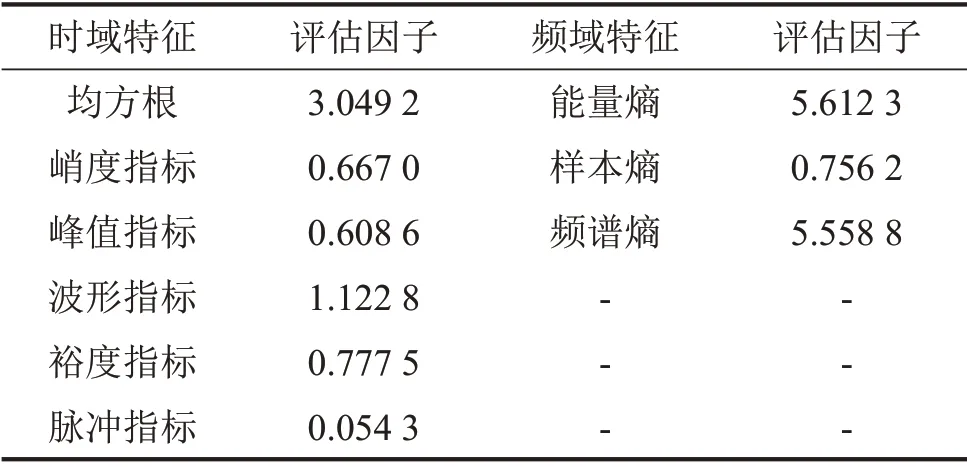
表5 评估因子

由表5可知，时域特征的敏感度为均方根＞波形指标＞裕度指标＞峭度指标＞峰值指标＞脉冲指标；频域特征敏感度为能量熵＞频谱熵＞样本熵。经验证，敏感度评估与对应的特征分布相吻合。因此，根据全特征参数的敏感度评估结果，选取时域中均方根和波形指标，频域中能量熵特征，组成24 维故障特征向量，2 种故障类型，每类110 个样本，共220 个样本组成敏感特征集用于RBF 神经网络进行训练及故障识别。

第四步，将敏感特征集输入RBF 神经网络进行故障识别。以24维故障特征向量作为网络的输入，定义轴承正常（1,0）、轴承故障（0,1）作为输出，当每类故障选取50组，共100组样本时，平均识别率只有60%，该情况由于样本数量较少，导致神经网络模型训练欠拟合，因此识别准确率较低。通过加大样本容量，每类110 组共220 组样本，随机分成训练样本和测试样本，测试20次神经网络对测试样本的识别准确率并取平均值，平均识别率为99.72%，平均耗时为1.5 s。

实验分析结果表明，在实际工况下，本文提出的改进降噪方法能够有效滤除轴承故障信号的噪声，基于类间、类内距离的特征评估方法筛选出的敏感特征对轴承故障具有良好的诊断效果。

5 结语

针对退火窑辊道轴承在强机械背景噪声干扰下的故障诊断问题，本文提出了基于灰关联熵分析的信号降噪和敏感特征评估的故障诊断方法。所提降噪方法能够有效降低原信号中的噪声干扰，基于距离的敏感特征评估方法能够从时域和频域特征中筛选出敏感特征，并利用RBF神经网络有效地识别出滚动轴承故障。滚动轴承实验和退火窑辊道轴承故障诊断实验均表明，本文提出的降噪方法简单有效，对轴承故障信号的信噪比和均方根值都有明显改善，基于距离的特征评估方法筛选出的敏感特征集，有效降低了特征维度，提升了故障诊断准确率。