基于密度聚类的塔机结构状态诊断方法

王胜春，安 宏，安增辉，李文豪

（山东建筑大学 机电工程学院，济南250101）

塔式起重机（以下简称塔机）是现代基础建设过程中非常重要的工程机械。随着我国经济的蓬勃发展，塔机使用的数量快速增加，塔机事故的发生率也逐年上升。如何保障塔机设备安全施工已经成为目前迫切需要解决的问题。

杨辉等[1]设计了塔机的远程监控系统，实现了不同区域内吊钩位置、力矩、吊重、高度和风速等多个参数的同步监测。訾旭昌[2]根据门座式起重机的空间姿态、应变和倾角等监测参数开发了门座式起重机健康状态监测系统。周凯笛[3]设计开发了基于工业嵌入式的结构健康监测系统，将其应用于正在服役的起重机械上。上述文献开发的监测系统可以实时掌握起重机的多个工作参数，对起重机进行状态监测，但对起重机钢结构的状态无法进行诊断。

文献[4]首先获取各点的位移变化率，然后利用支持向量机进行分类，对塔机钢结构进行状态判别。文献[5]采用自由振动分析方法对钢柱和钢框架结构进行了试验和数值研究。研究发现，由于裂纹的存在，结构的力学性能会发生变化，从而导致模态频率降低。邢哲等[6]以结构损伤前后的频率平方变化率和标准化位移振型进行组合，作为神经网络的损伤指标进行学习和判断，研究了网架钢结构的损伤识别。张冲等[7]研究了光纤传感器在起重机械安全监测中的应用，记录了起重机工作过程中的应变曲线。这些方法都可以检测结构的状态，但前提是需要设置大量传感器，并且需要损伤状态的数据进行大量学习，才可以获得较好的效果。但是获得大量真实的塔机损伤数据是非常难的。塔机事故不同于其他事故，塔机事故较多的是重大事故，而这些都限制了上述方法在塔机结构状态诊断中的应用。

密度聚类(Density-Based Spatial Clustering of Applications with Noise，DBSCAN)是一种基于密度的聚类算法，这类密度聚类算法一般假定样本的类别可以通过样本分布的紧密程度决定。同一类别的样本，它们之间紧密相连，在该类别任意样本周围不远处一定有同类别的样本存在。密度聚类可以对任意形状的稠密数据集进行聚类，它根据数据的内在联系，对数据自动分类。

本文提出一种基于时间序列分析和密度聚类相结合的塔机结构安全状态诊断方法。首先建立QTZ315 塔机（起重力矩为3 150 kN·m 的塔式起重机）的有限元模型，验证模型的有效性，提取塔机结构在起升动载荷下的动态位移。然后对塔机的动态位移进行时间序列分析，提取通过自回归模型提取数据的残差的方差和位移均值作为塔机状态的特征值。通过完好工况的特征值求解密度聚类的自适应半径r，解决了该密度聚类算法半径r需要按照经验设定的问题。将归一化的特征值进行自动聚类分析，实现了塔机结构状态的自动诊断。最后通过单肢实验对该方法进行实验验证。

1 塔机模型建立与验证

在有限元软件中，塔机钢结构的主肢、水平腹杆、斜腹杆、上弦杆和下弦杆等构件均用梁单元Beam188模拟，塔机拉杆用杆单元Link180模拟。

（1）对研究问题影响不大的结构进行适当的简化：将上支座和下支座等实体采用梁单元加固等效处理。将塔机平衡重、变幅机构等质量集中的塔机附件，用质量单元Mass21等效处理[8]。

（2）对边界条件的处理：起重臂和平衡臂与回转塔身之间通过销轴链接，在ANSYS有限元模型中采用耦合处理，仅释放销轴转动方向的自由度，塔身底部的基础节用地基螺栓将其固定在地面上，在模型中约束底部4个节点的所有自由度。

该QTZ315 塔机所有的杆件在ANSYS 中的材料属性根据实际情况和塔机型式检测报告[9]设定为：弹性模量为210 GPa、泊松比为0.3、密度为7 800 kg/m3。为了在构建模型的时候，容易建立模型和方便后续操作，该模型以塔身竖直方向为Y方向，以起重臂方向为X方向，在水平面内以垂直X方向向外的方向为Z方向。模型结构如图1 所示。具体的损伤位置如图2所示。圆圈内标号为L2的单元为损伤单元，损伤单元占单个标准节主肢长度的5%。通过塔机型式检测报告验证模型的有效性。

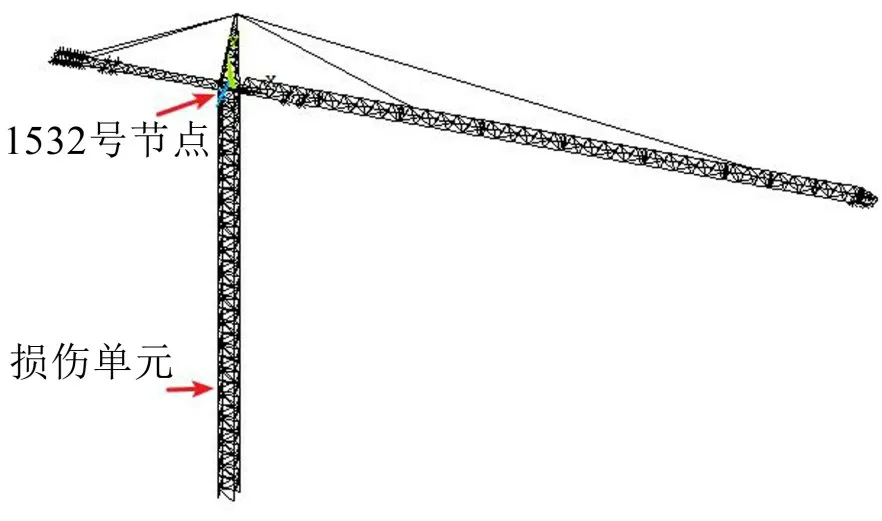
图1 模型结构图

图2 损伤处放大图

该QTZ315塔机的技术参数为：起升高度48 m；起重臂最大工作幅度70 m；起重臂最大工作幅度处额定起重量3 440 kg；塔机最大额定起重量16 000 kg；起升速度0.525 m/s；吊重在3.6 s 末离地。根据文献8 中的方法计算额定起升激励载荷，施加到幅度70 m 处，设置载荷步和阻尼，利用完全法对塔机模型进行瞬态动力学分析。

本文主要研究的是塔身钢结构的损伤，在模型分析中用弹性模量E的消减模拟结构损伤。模拟损伤的位置见图1，损伤单元位于塔身平衡臂侧第二标准节顶端，图2为该区域放大图。针对以下3种塔机结构损伤状态进行研究：

（1）塔机结构完好（工况1）；

（2）塔身平衡臂侧第二标准节顶端的损伤单元损伤80%，即弹性模量消减80%（工况2）；

（3）塔身平衡臂侧第二标准节顶端的损伤单元损伤60%，即弹性模量消减60%（工况3）；

（4）塔身平衡臂侧第二标准节顶端的损伤单元损伤50%，即弹性模量消减50%（工况4）。

利用ANSYS的后处理模块，提取回转平台与损伤主肢同侧的主肢上的节点1532 号的动态位移信息，对其进行状态分析。

2 特征提取

2.1 模型建立与特征提取

自回归模型（Autoregressive Model，AR模型）是现在常用的时间序列模型之一。利用AR 模型对塔机的动态数据进行损伤特征提取。首先将采集到的塔机结构的动态位移信号进行数据标准化处理，记录为时间序列{Xt} ，根据完好状态下的数据建立自回归模型AR(p)为：

式中：p为自回归模型的阶次；

ai为自回归参数；

εt为模型的残差。

步骤1：应用贝叶斯信息准则（Bayesian Information Criterion，简称BIC 准则）和Burg 递推法估计出模型的阶次和模型参数。

步骤2：将多组数据得到的参数取均值，得到各个参数的均值，利用参数的均值建立AR模型。

步骤3：再利用待检状态的数据去拟合步骤2建立的AR模型，获取各组数据的残差的方差。

如果结构状态不变，那么模型将适用于当前数据，残差应该在较小的范围内。如果结构出现损伤，模型就会出现偏差，那么在系数不变的情况下，所有结构上的变化全部累积到AR 模型的残差之中，偏差应该加大。因此将残差的方差设为特征值之一。

步骤4：为了保留原数据的特征，将动态数据的均值作为另一特征值，这样弥补了前期对数据进行了标准化处理造成的信息的缩减。

2.2 基于密度的诊断算法

基于密度的聚类（DBSCAN）根据数据点的局部密度来确定类别[10-12]，而不是仅仅通过点与点之间的距离。基于密度的聚类算法的基本步骤如下所示[13-14]：

步骤1：设定半径r和阀数M，计算数据集中每个点与其他点之间的距离。并判断该点是否可以成为核心点。同时给每个点设置标识符，表示这些点没有赋给任何一个簇。核心点的判定规则为：在某一点在半径r距离以内的点至少有M个，则这一点为核心点。

步骤2：从未分配的核心点开始，找出它所有密度连通的点，并分配给其中一个簇。如果某些边界点属于从多个核心点距离可达，则把这些边界点分配给任意的核心点，也可以同时赋予给所有的簇。边界点的判定规则：该点不是核心点，但是它在某个核心点的半径r距离以内。

步骤3：不属于任何簇的点作为噪声点处理。

因为密度聚类的簇是根据数据密度自动划分的，所以密度聚类可以处理任意形状和大小的数据集。但是密度聚类的一个局限在于，它对于半径r的要求比较高。如果半径r太大，较密集的簇容易被合并到一起；如果半径r太小，较稀疏的簇容易被分成多个簇。目前，半径r的取值主要是依靠经验确定。

因为在塔机损伤识别过程中，以完好状况的塔机数据和待测的塔机数据做两两对比，所以只要确定可以使完好状况的塔机数据或者待测工况归类成一簇的最小半径r，就可以解决密度聚类的局限。因此本文提出自动计算出自适应半径r的步骤：

步骤1：计算每个数据点与其他数据点之间的距离，从小到大排列每个点到其他点的距离，选取每个点与其他点的第M个距离值；

步骤2：从步骤（1）选取的距离值中，选取最大值rmax，以[0，rmax]为区间，用区间消去法，求出最小半径rmin；

步骤3：利用步骤1～2 求出完好工况和检测工况的最小半径rmin，对比各工况的最小半径rmin，选择其中较小的为密度聚类的半径r。

此方法在塔机损伤识别中可以解决密度聚类的半径局限。经过多个数据集的检验，此方法可以使用。

3 仿真结果分析

用节点1532号Z方向的动态位移对塔机进行分析。首先取1532号的完好工况（工况1）的动态位移10 组，每组数据个数N取100，用BIC 准测对AR 模型阶次进行确定，如图3所示。

结果发现，用BIC 准则进行定阶时，由图3 可知，BIC 值从p=11 开始，其下降速率减慢，BIC 值逐渐平稳。根据密度聚类分析的特性和BIC准则中的要求，把该AR 模型的阶次设定为p=11。用完好状况塔机的数据建立AR(11)模型，按照2.1 节中步骤求出参数ai的均值，如表1所示。

表1 完好状况塔机（工况1）数据的参数的均值

图3 定阶

利用表1 中的参数的均值建立检测AR(11)模型。分别取工况1 和工况2 两种工况下塔机的动态位移数据，去拟合上述的检测AR(11)模型，求出两种工况的残差的方差和数据的均值。把两种工况的残差的方差和数据均值进行标准化处理（归一化处理），特征值如表2所示，1～10组为工况1的特征值，11～20组为工况2的特征值。

设定基于密度的聚类方法的M为4，同时利用表2 的1～10 组数据根据2.2 节中的步骤，自动计算出自适应半径r为0.023 4。将表2 的数据利用DBSCAN 聚类方法进行塔机状态自动诊断，自动判定结果如图4所示。

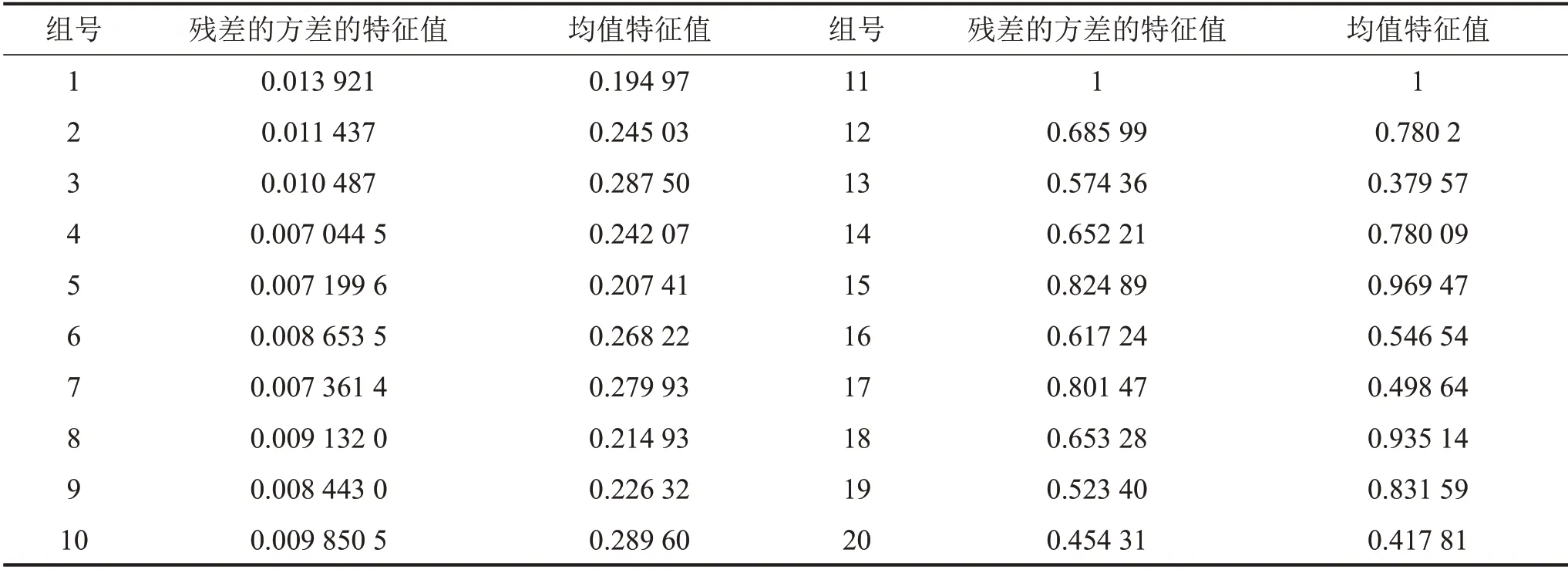
表2 塔机工况1与工况2状态塔机的特征值

由图4可知，塔机正常状态的数据（工况1）和损伤状态的数据（工况2）被自动诊断分为两类，正确率为100%，可以实现塔机损伤预警和损伤诊断。同样用上述步骤对塔机工况1与工况3状态进行分析，设定基于密度的聚类方法的M为4，自动计算出自适应半径r为0.130 9，结果如图5所示。

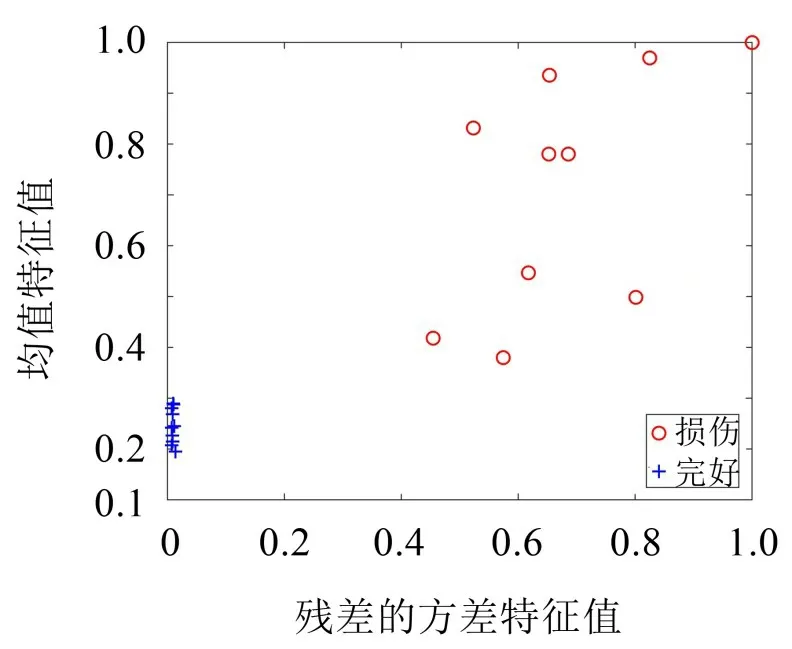
图4 塔机工况1和工况2的判别图

图5 塔机工况1和工况3的判别图

由图5可知，塔机正常状态的数据（工况1）和损伤状态的数据（工况3）被自动诊断分为两类，正确率为100%，可以实现塔机损伤预警和损伤诊断。对塔机工况1与工况4状态进行分析，设定基于密度的聚类方法的M为4，自动计算出自适应半径r为0.162 1，结果如图6所示。

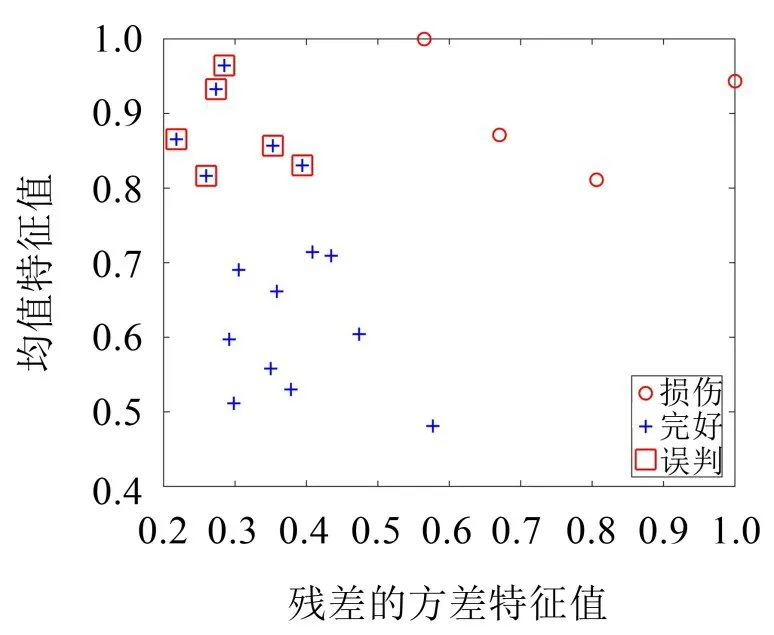
图6 塔机工况1和工况4的判别图

由图6可知，塔机正常状态的数据（工况1）和损伤状态的数据（工况4）被自动诊断分为两类，正确率为70%。从上述分析可以看出本方法可以对损伤程度50%进行损伤识别，虽然出现了误判，但是没有出现错误预警。

通过分析可以看出本方法可以比较准确判断塔机的损伤，分析所用的数据，只用了从塔机模型回转平台1532 节点提取的位移数据。通过单肢实验数据对此方法进行验证。

4 单肢实验研究分析

为了验证本文方法的有效性，设计了塔机的单肢实验，用单肢实验数据对上述方法进行验证。把型号为FTZ6010塔机的两根标准节的主弦杆作为实验对象。两根主弦杆之间采用M36X3 的高强度螺栓连接。使用液压缸对实验构件进行偏载加载，最大压力为25 MPa。在实验中，通过松动连接两根主弦杆之间的高强度螺栓模拟塔机损伤。振动数据由安装在顶端下弦杆上的倾角测量传感器获取。实验台设计图和实物图如图7和图8所示。

图7 实验台设计图

图8 试验台实物图

单肢实验的过程如下步骤：

步骤1：开始给实验台液压缸进行加压，主弦杆受拉力的影响，当拉力逐渐增加到20 t时，停止对液压缸加压；

步骤2：开始保持液压缸压力不变，时间为30秒；

步骤3：保压结束后，液压缸给系统卸压到拉力为0；

步骤4：每种工况重复上述步骤三次。

采用本实验的两个工况进行分析，分别是：

工况1（完好工况）：对连接两根标准节主弦杆之间的两个高强度螺栓分别施加700 N·m 的预紧力，即螺栓连接状态正常。

工况2（损伤工况）：其中一个高强度螺栓松开2扣，另一个高强度螺栓施加和工况1相同的预紧力，即700 N·m的预紧力。

实验数据与上述仿真结果分析的振动数据的方向相同。对实验数据进行损伤识别分析，首先每个工况分别选择9组实验数据，每组选取100个点。通过BIC准则对其进行定阶分析，如图9所示。

图9 单肢实验数据定阶图

通过工况1的数据建立AR(3)模型，求得该模型的参数均值，如表3所示。

表3 单肢实验完好状况（工况1）数据的参数均值

用上述2.1 节和2.2 节的步骤对单肢实验工况1和工况2进行分析。特征值如表4所示1～9组为工况1，10～18组为工况2。设定密度聚类的M为4，自动计算出自适应半径r为0.048 8，分析结果如图10所示。

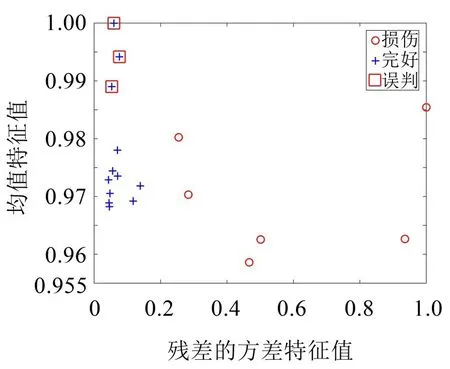
图10 单肢数据工况1与工况2判别图

表4 单肢实验数据的工况1和工况2特征值

由图10 可知，单肢实验工况1（完好状态）数据和工况2（损伤工况）数据被自动诊断分为两类，正确率为83.3%。通过实验分析看出，密度聚类可以把损伤特征值根据计算的半径自动分成两类，虽然在单肢实验工况2 在自动诊断中正确率只有83.3%，但是没有出现错误预警，可以判定单肢实验数据工况2出现了损伤。

5 结语

目前塔机结构损伤诊断的研究中有的用人工智能进行前期训练和后期诊断，有的用大量传感器进行监测，本文提出了用单个传感器进行自动诊断的方法。以完好状态的塔机信号进行时间序列分析，建立AR 模型,求得该模型的参数均值，用完好状态和损伤状态的位移数值拟合模型，用计算出的残差和各组数据均值作为特征值。自适应计算聚类半径，进行结构状态的自动诊断。仿真数据结果表明，此方法可以对塔机模型第二标准节上端微小单元弹性模型消减50%以上的工况准确判断损伤。对单肢实验结果分析表明，此方法可以识别结构状态，可以实现塔机完好状态和结构损伤状态的智能判别。本文方法克服了塔机损伤数据难以获取，因而难以用人工智能进行训练的难题，仅需完好工况的塔机数据就可以完成塔机的结构状态诊断，且只需要非常少的传感器即可实现。