一道2021年高考压轴题的多视角探究
2021-10-22福建师范大学数学与信息学院350117束浩东
福建师范大学数学与信息学院 (350117) 束浩东
近年来全国高考和各地的模考试卷中频频出现导数的极值点偏移问题,该类型试题通常以压轴题的形式出现,对考生的数学思维能力和基本功要求较高.文章以2021年新高考数学1卷的压轴题为例,对一类极值点偏移问题进行了多解探究,总结了证明此类问题的常见方法和思路,在此基础之上对该题的“母题”进行了优化证明.
1 原题再现

2 试题解析
问题(I)的求解:由f(x)=x(1-lnx)得f′(x)=-lnx.分别令f′(x)>0得0
下面主要是对问题(II)的证明进行探究.

思路一:构造函数,对称作差
证明:(1)先证x1+x2>2,即证x2>2-x1.因为0

图1
(2)再证x1+x2 图2 评注:本题是一道老生常谈的“极值点偏移”问题,求解的关键在于揭开试题“神秘的面纱”,不被其表象迷惑.由于原函数中含有对数函数,因此在比较大小时考虑使用作差法较为简洁.根据函数特点画出草图,可使解题思路更为清晰明了!利用对称作差构造函数是解决此类问题的基本思路,当然,笔者对后半部分的证明过程当中用到了部分高数知识,对于高中生来说可能不太适合.因此在这里留下一个瑕疵,期待有更为完美的处理方法. 思路二:等价变形,换元转化 图3 评注:实际上方法一和方法二如出一辙,相对方法一而言,方法二的难度在于如何将题设条件blna-alnb=a-b合理变形,通过巧妙换元把问题转化为研究函数g(t)=tlnt(t>0)的极值点偏移问题,因此该方法具有一定的技巧性和创造性,对考生的数学思维能力要求较高. 思路三:巧用放缩,妙解问题 (2)再证明x1+x2 评注:可以说对数平均不等式是解决极值点偏移问题的一大有效“杀手锏”,根据题设条件合理进行变形转化往往可以获得事半功倍的良好收益.第二部分证明的关键点在于能否发现并利用“1-lnx1>1,1-lnx2<1”这一隐藏结论,运用放缩法研究不等式问题对学生而言具有一定的挑战性,不仅要掌握一定技巧还需对常见基本函数的相关结论如“lnx≤x-1,(x>0)”有一定的积累.教师在日常教学中应注意归纳和整合相关知识,帮助学生建构自己的知识网络以我完善学生的数学认知结构,助力学生数学学科核心素养的达成. 思路四:合理代换,化难为易 A.(1)(2) B.(1)(3) C.(2)(3) D.(1)(2)(3) 结论(3)即为本文原题第(2)小问的前半部分,不再阐述. 作为数学教育工作者,应从不同的视角深入探究,不断优化解题过程,发掘试题背后所蕴含的价值.高考评价体系中也强调“经过素质教育的培养,学习者应当能够从多个视角观察、思考同一个问题;能够灵活地、创造性地运用不同方法,发散地、逆向地解决问题”.由此可见,多视角探究问题既是考试评价要求也是培养学生发散性思维和创新精神的重要途径.基于此,笔者认为在数学解题教学中应充分发扬试题的辐射作用,鼓励学生从不同层次对问题展开探究,寻找不同的解题方法,从“就题论题”上升到“就题论法”,避免机械式的题海战术.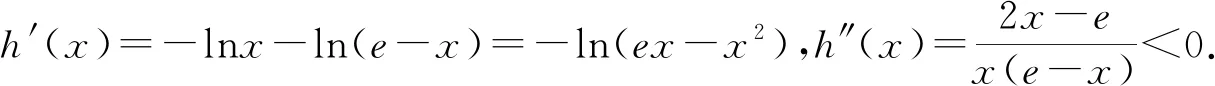
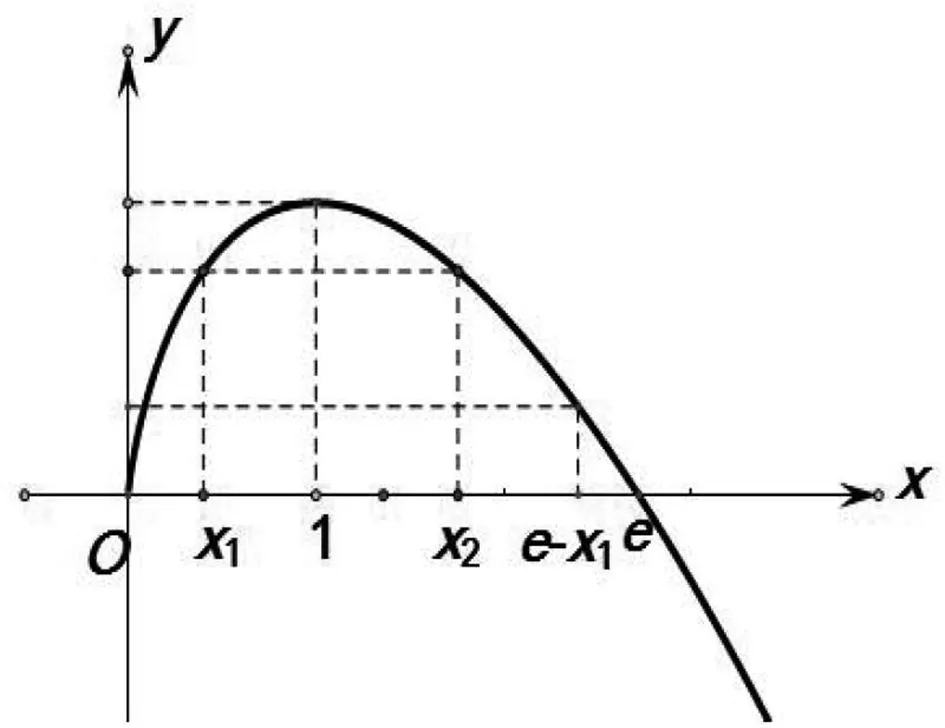
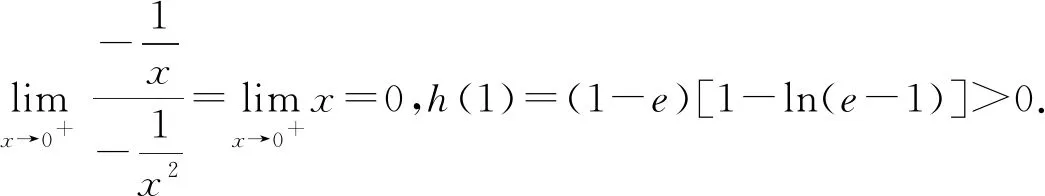

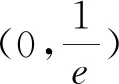
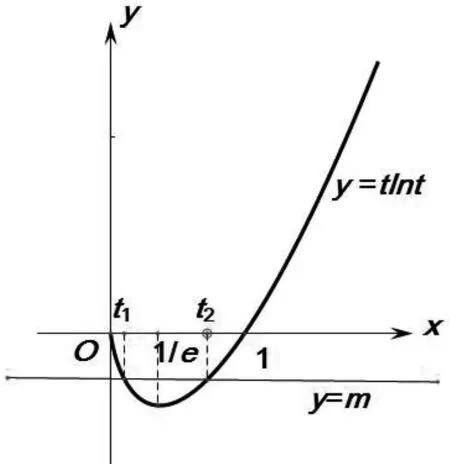





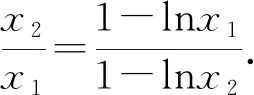



3 题源探究




4 写在最后
