构建不等式求解参数取值范围问题的策略
2021-10-22福建省石狮市第八中学367200陈钟洪
福建省石狮市第八中学 (367200) 陈钟洪
在高考数学试卷中,时常出现求参数取值范围的试题,即以借助构建不等式为条件的题型的考查,该类题型不仅考查学生利用函数定义域、值域、单调性、恒成立条件等条件构建不等式解出范围的能力,而且这类问题涉及的知识面广、综合能力强、思维层次高,能较好地考查学生的数学抽象、逻辑推理、直观想象、数学运算等数学核心素养,一直都是历年高考命题的热点和重点.本文结合近年高考试题,对此类问题进行归纳,剖析制约求参数范围的成因,并由此探讨其解题对策.
1.利用函数定义域、值域构建不等式解范围
某些未知参数与某已知量之间存在某等量函数关系,处理这类问题时,则可通过已有知识挖掘出它俩之间的等量函数关系,把未知参数化为关于已知量的函数,从而根据已知量的定义域、值域的不等式范围求出未知参数的取值范围.

A.(1,3) B.(1,3]
C.(3,+∞) D.[3,+∞)
解析:如图1,易知P在双曲线的右支,设|PF2|=m,则|PF1|=2m,结合|PF1|=2|PF2|知|PF1|-|PF2|=m.设∠F1PF2=θ(0<θ≤π),且由双曲线定义|PF1|-|PF2|=2a,从而有2a=m,于
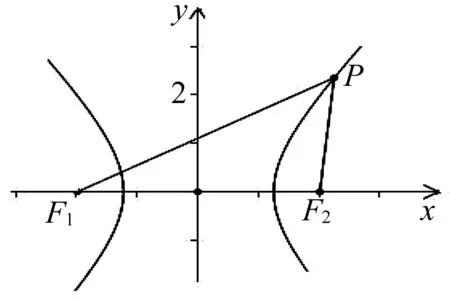
图1
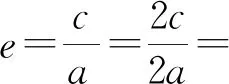
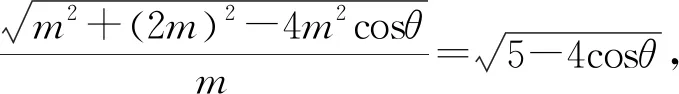
2.利用函数性质构建不等式解范围
高考对求参数范围与函数性质综合的考查最近几年略多一点,典型的题型有:(1)利用函数的单调性构造不等式;(2)利用分离参数法构造参数与函数最值的不等式.
(1)利用特殊函数的单调性来构造不等式
某些参数取值范围常以一些特殊单调函数如一次函数、二次函数在局部区间内、对数、指数函数等函数来呈现.因此,可利用这些函数单调性的性质,构建不等式,解出参数范围.这类问题可很好培养学生的数学抽象、逻辑推理、数学建模等核心素养.
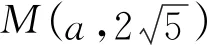
(1)若|MF|=6,求抛物线的标准方程;

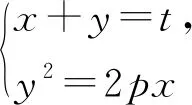
(2)利用分离参数法构造参数与函数最值的不等式
某些参数取值范围常与恒成立不等式结合起来考查.可通过分离参数法,将参数从恒成立不等式中化归转化,从而构建参数与函数的最值的的不等式并解出范围.一般有如下结论:若对于x取值范围内的任何一个数都有f(x)>g(a)恒成立,则g(a)
例3 (2020年全国Ⅰ卷适合于山东21)已知函数f(x)=aex-1-lnx+lna.
(1)当a=e时,求曲线y=f(x)在点(1,f(1)处的切线与两坐标轴围成的三角形的面积;
(2)若f(x)≥1,求a的取值范围.
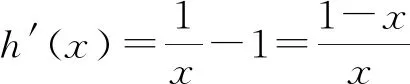
3.利用图象法巧妙构建不等式解范围
在允许范围内都有f(x)>0(或f(x)<0),则在这个范围内f(x)的图像都在g(x)的图像上方(或下方),从而由观察图象构建f(x)与g(x)的不等关系,即构造出参数的不等式,并解出范围.此类问题可以很好的培养学生的直观想象、逻辑推理等核心思想.
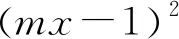
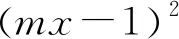
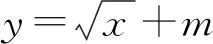
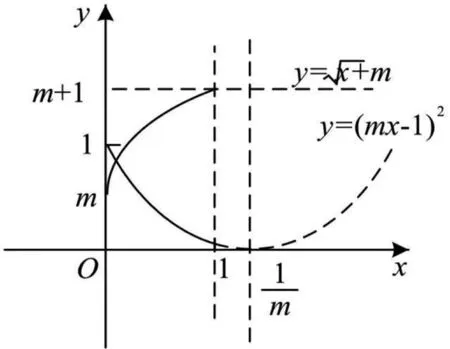
图2
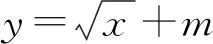

图3
4.利用题目中隐藏的已知参数的范围构建不等式解范围
此类问题须根据题意及内在联系,推出要求参数与题目已知参数之间的关系,利用已知参数的取值范围进而建立所求参数的不等式,并解出范围.该类问题可以很好的培养学生的数学抽象、逻辑推理等核心思想.
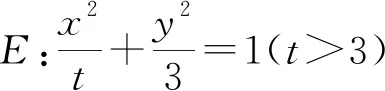
(1)当t=4,|AM|=|AN|时,求△AMN的面积;
(2)当2|AM|=|AN|时,求k的取值范围.
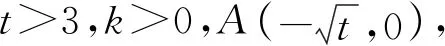
5.合理联想,运用平几性质构建不等式解范围
有些圆锥曲线研究某直线与圆恒有交点求参数取值范围的问题,由于题设中有两个参数,用解析几何中有交点的理论将二方程联立,用判别式来解题是比较困难.若考虑到直线过定点,且曲线为圆,则可运用平几性质,想到必须定点在圆上或圆内,从而构建不等式,求出参数取值范围.这类问题可培养学生直观想象、逻辑推理等核心素养.
例6 不论k为何实数,直线y=kx+1与曲线C:x2+y2-2ax+a2-2a-4=0恒有交点,求a的范围.
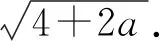
6.分类讨论,利用函数构建不等式解范围
关于二次函数的问题主要可以总结如下:
(1)若二次函数y=ax2+bx+c(a≠0)大于0恒成立,则有a>0且△<0;
(2)二次函数在指定区间上的恒成立问题可以利用韦达定理以及根的分布理论求解.
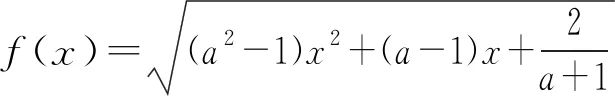
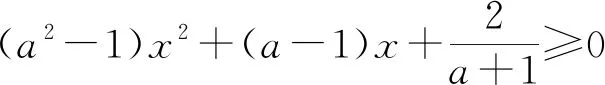
本文主要是分析了几种需要通过构建不等式能解出参数范围的常见题型,着重研究它的题型特点、解题方法以及思路形成的规律,旨在教学实践中切实帮助学生提高分析解决问题的能力,培养一定的数学核心素养.
