热传导方程的积分变换求解与MATLAB实现

2021-10-22欧志华奉瑞萍

湖南科技学院学报 2021年3期

丁波欧志华奉瑞萍

丁波欧志华奉瑞萍

（湖南工业大学土木工程学院，湖南株洲 412007）

热传导方程是物理学中经典方程之一，反映热的作用规律。有关热传导方程的解法有分离变量法、延拓法、特殊函数法、积分变换法等。本文首先介绍Fourier变换和Laplace变换在求解热传导方程中的应用，然后以抛物型方程Heat Equation为例，给出了通过MATLAB中的偏微分方程工具箱PDE Toolbox进行建模求解及模拟直观。通过空间中的温度场分布和梯度方向，发现温度是由温度高的一面向低的一面变化，而且最靠近热源的分子首先被加热，经过一段时间，温度场中每一点都非常接近与它所能到达的最高温度，逐渐趋于稳态。

热传导方程；Fourier变换；Laplace变换；MATLAB实现

热的作用服从于一些不变的规律，如果不借助数学工具分析就不能精确地发现和了解这些规律。法国数学家和物理学家傅里叶(Jean-Baptiste-Joseph Fourier，1768-1830)，最早建立热传导方程来研究热的作用规律，1807年，他向科学院提交的论文《关于热传导的研究报告》中建立了关于不连续的物质和特殊形状的连续体的热扩散（即热传导）方程。和重力、磁场一样，热贯穿于宇间的一切物质之中，热传导方程是物理学经典方程之一，反映了温度在空间中如何变化[1]。热传导方程是二阶线性偏微分方程，解的呈现形式复杂且多样，孙桂荣[2]等运用Nevanlinna值分布理论讨论了二阶线性微分方程解的径向振荡问题，杨琰琰[3]等运用Nevanlinna值分布理论和方法考察了一类针对非线性差分方程解，并得到解的增长性和表示，对于求解热传导方程的数学方法有很多，其中针对齐次方程的有分离变量法、无穷级数法等[4]，针对非齐次方程的有函数变易法、齐次化原理[5-6]、特殊函数法[7]等等。积分变换法[8-10]通过将偏微分方程转化为常微分方程或代数方程，而且不论是求解齐次方程还是非齐次方程，以及对于无界问题和半无界问题的求解，都避开了复杂的函数处理技巧与求解运算，十分方便得到方程的解。本文主要介绍Fourier变换和Laplace变换在求解热传导方程中的应用，另外利用编程和可视化极强的软件——MATLAB求解偏微分方程[11]，可以直观地反映空间中的温度场是如何变化的，并可以得到温度梯度的方向，这对于指导实际工程有很大的指导意义。

1　热传导方程及其定解问题的导出

1.1 热传导方程

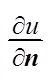
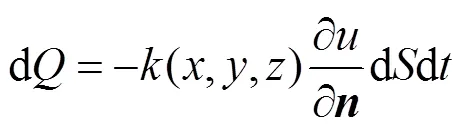
其中(,,)称为物体在点(,,)处的热传导系数(＞0)，等式右边的负号表示热流的方向与温度梯度相反，由于热量总是从温度高的一侧流向低的一侧。

在物体G内任取一封闭曲面Γ，它所包围的区域记为Ω，从时刻1到2流进此闭曲面的全部热量为

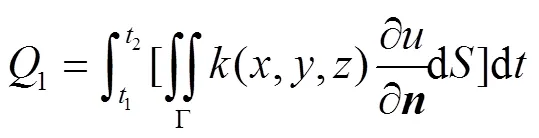
流入的热量使物体内部温度发生变化，则在同一时间段(1,2)内，它所吸收的热量为

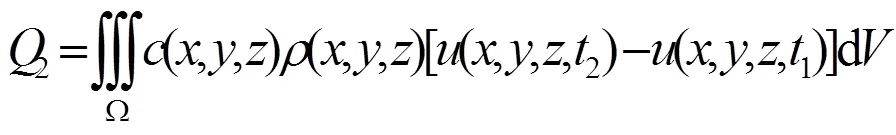
其中为比热，为密度。若物体内没有热源，则根据热量守恒定律，得1=2，即

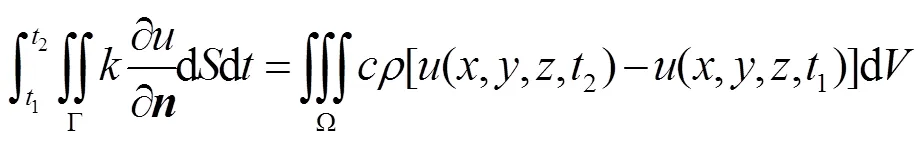
假设函数关于空间变量,,具有二阶连续偏导数，关于时间具有一阶连续偏导数，利用高斯公式[12]将第二型曲面积分转化为三重积分，上式整理为

此为非均匀各向同性体的热传导方程。若物体均匀，、及均为常数，记/=2，有

上式称为三维的齐次热传导方程，若物体内部有热源，设热源密度即单位时间内、单位体积内发出的热量为(,,)，记(,,,)=(,,)/，得非齐次方程[9]

1.2 定解问题

Fourier所做的工作就是将诸多不同情况的热扩散（或热传导）问题，转化为在不同边界条件和不同初始条件下的求解。从物理学的角度来看，如果知道了物体在边界上的温度分布（或热交换状况）和物体在初始时刻的温度，就可以完全确定物体在接下来任意时刻的温度分布，因此热传导方程的定解问题就是在已给定的初始条件与边界条件下求问题的解。对于热传导方程的初始条件的提法显然为

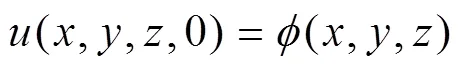
其中(,,)为已知函数，表示物体在=0时的温度分布。三类边界条件如下：

1）物体的表面的温度是已知的，为

其中Γ表示物体的边界曲面，(,,,)是定义在(,,)∈Γ，0≤≤T上的已知函数，此称为热传导方程的第一类边界条件(又称狄利克雷(Dirichlet)边界条件)；

2）温度函数在表面上的外法向方向导数是已知的，为

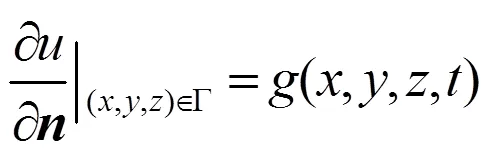
此称为热传导方程的第二类边界条件(又称诺伊曼(Neumann)边界条件)；

3）温度函数及其外法向方向导数的现行组合在界面上是已知的，为

其中为已知正数，此称为热传导方程的第三类边界条件。

上述的三类边界条件加上方程构成的定解问题分别称为：第一边值问题(Dirichlet问题)，第二类边值问题(Neumann问题)和第三类边值问题(Robin问题)。

2 Fourier变换求解热传导方程

2.1 Fourier变换定义及其性质

定义：设()是定义在(-∞,+∞)上的绝对可积函数，且在任意有限区间上满足Dirichlet收敛条件，则称函数

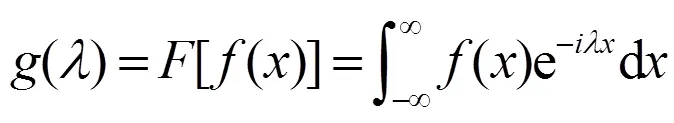
为()的Fourier变换，记为[]；称函数

相比较于分离变量法中用Fourier级数来求解热传导方程，Fourier变换可以看作是Fourier级数的极限形式，是将一种代表某种关于时间或空间的信号（signal）从时域转换到频域内表达的手段。

性质1：线性性质：对于任意复数α，β以及函数1，2,成立

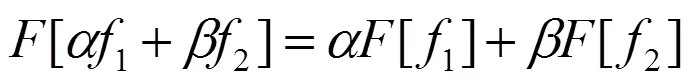
2.2 一维热传导方程的初值问题(无界问题)

定解问题(1)中的方程和初始条件两边关于作Fourier变换，记

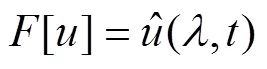
利用2.1节Fourier变换的性质，(2)代入(1)中得

方程(3)是一阶线性非齐次常微分方程，可由常数变易法得

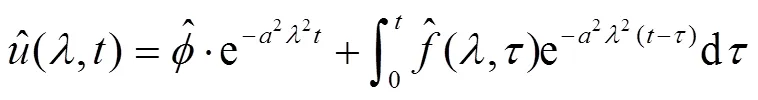
然后对方程(4)两边求反演，记

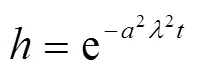
则

因为

很容易得

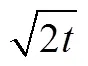
同理可得

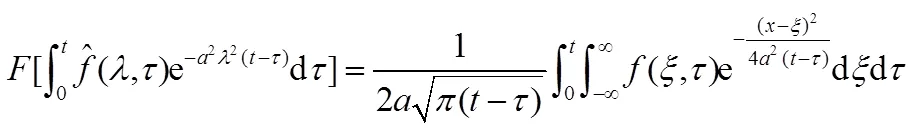
利用2.1节Fourier变换性质2和叠加原理得

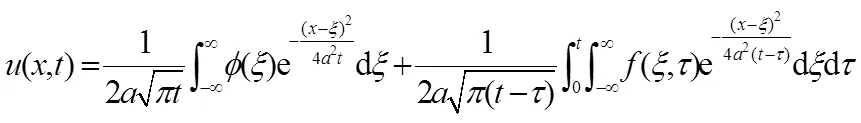
此即为用Fourier变换法求得一维热传导方程问题的解。

同理，也可得到二维热传导方程柯西问题

解的表达式为[13]

3 Laplace变换求解热传导方程

3.1 Laplace变换定义及其性质

因为Fourier变换要求函数在(-∞,+∞)上有定义，如果我们研究的半无界问题（混合问题），则不仅不能对进行Fourier变换，而且也不能对进行变换(≥0)，为此，对于定义在≥0中的函数()，考虑Laplace变换，通过Laplace变换将微分方程转化为常微分方程或代数方程[14]。

定义：对于函数()，函数

为()的Laplace变换，记为[]；称函数

为()到()的Laplace逆变换，记为-1[].

性质1：线性性质：设∀1、2，由Laplace变换的定义，得

性质2：微分性质：设函数()的导函数的Laplace变换存在，则有

一般地，有

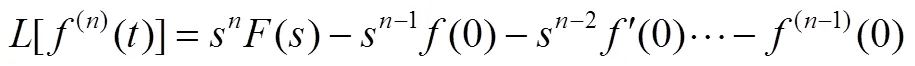
性质3：卷积性质：

3.2 Laplace变换求解热传导方程的混合问题

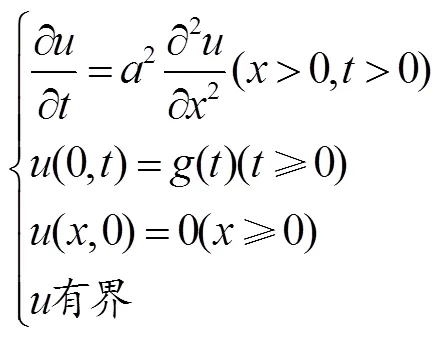
方程(10)与边值条件(11)两边关于作Laplace变换，记

利用3.1节Laplace变换的性质1和2，得

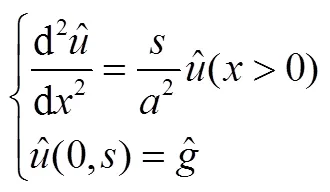
可见，通过Laplace变换使原本偏微分方程(9)转化成常微分方程(11)，易得其特解为

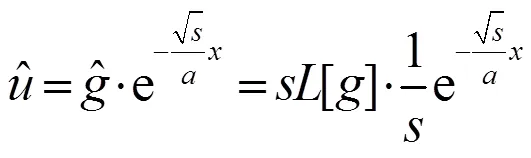
记

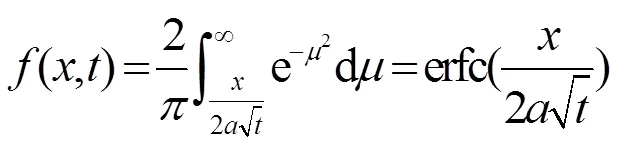
因为

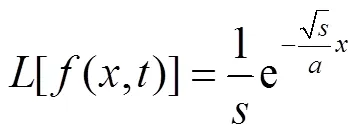
代入(12)式中，并由卷积性质3，得

其中

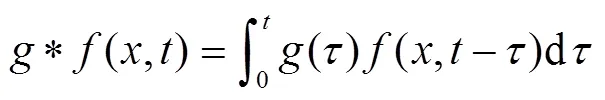
由(,)的表达式(13)及(15)，得

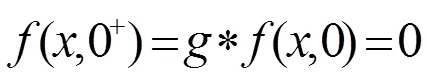
因此，利用微分性质2，得[15]

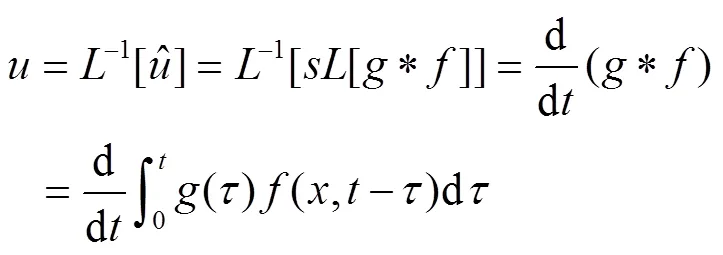
4 MATLAB中求解热传导方程

根据积分变换法得出热传导方程的解含有空间坐标函数和时间函数，从解的形式上来看，很难直观看出热的传导规律，温度场的变化和温度梯度的方向。MATLAB是具有极高编程效率和强大作图功能的科技应用软件之一，通过MATLAB中的偏微分方程工具箱(PDE Toolbox)对抛物型方程(Heat Equation为例)进行求解。为研究热在介质中的扩散规律，现考虑一个带有矩形孔(孔长0.8，宽0.1)的金属板(板长1.6，宽1)的热传导问题，板的左边界保持在100℃，板的右边界热量从板向环境空气定常流动，其余各边界保持绝缘。初始条件=0时板的温度为0℃，由上述条件可得到该定解问题为：

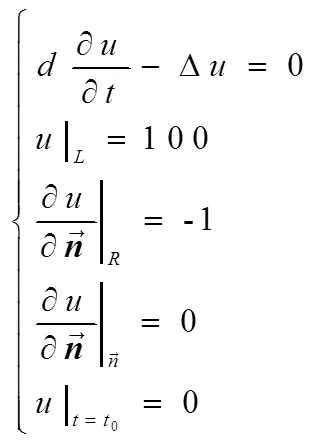
因为在MATLAB中对于抛物型方程的一般形式为：

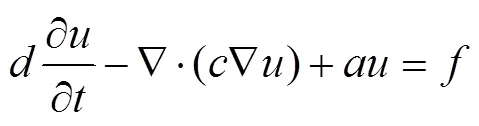
其中=(,)，、、和是标量复函数形式的系数，所以在PDE Specification中设置方程为抛物型（Parabolic），=1，=1，=0，=0；左边界为狄利克雷（Dirichlet）条件：=1，=100；右边界为诺伊曼（Neumann）条件：=－1，=0；其余边界为诺伊曼（Neumann）条件：=0，=0。

方程建立、设置边界条件和网格划分，经过计算，分别给出Time=0，1，3，5，10，100时刻的温度场和梯度图：

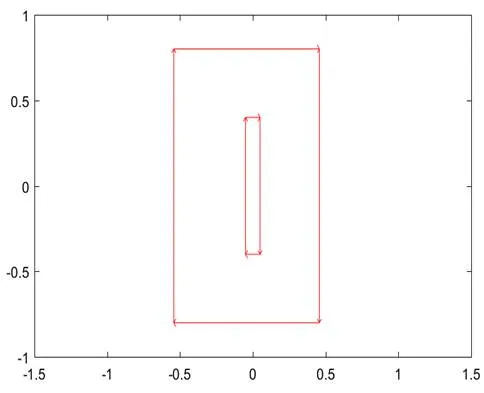
图1 建模、边界条件建立

图2 网格划分

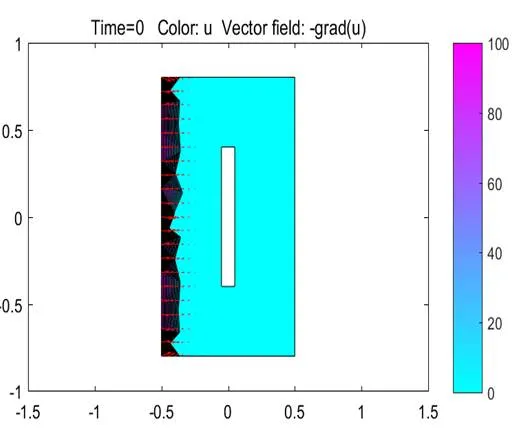
图3 Time=0时刻的温度场和梯度方向

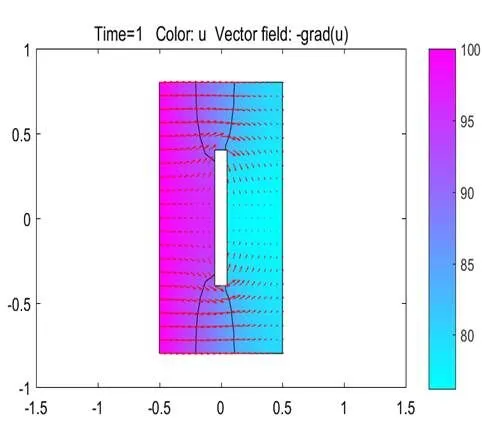
图4 Time=1时刻的温度场和梯度方向

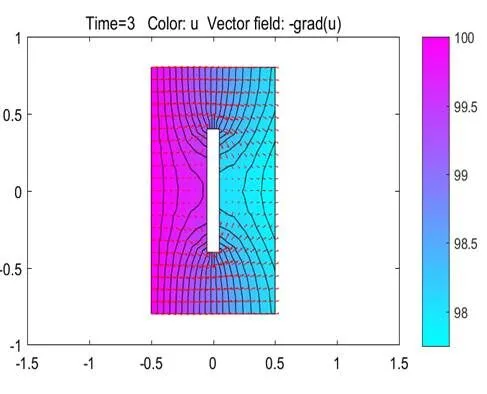
图5 Time=3时刻的温度场和梯度方向

图6 Time=5时刻的温度场和梯度方向

图7 Time=10时刻的温度场和梯度方向

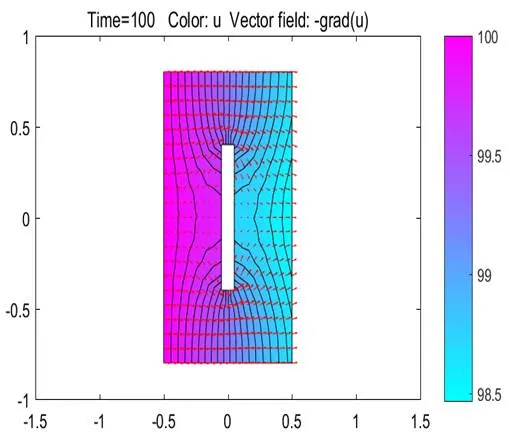
图8 Time=100时刻的温度场和梯度方向

可以发现板内温度是由温度高的一面向低的一面变化，而且最靠近热源的分子将首先被加热，经过一段时间后，金属板的每一点都将获得非常接近于它所能达到的最高温度。在Time=10之后至Time=100板内温度变化不大，也就是说随着时间越来越长，板内的温度也逐渐趋于稳态。每个点的最高温度取决于距离热源的距离，且温度随离热源越远而越低。

5 结束语

热传导方程是反映了温度变化的规律，通过积分变换法应用于热传导方程的求解十分简便，积分变换的核心是求象函数的逆变换，通过卷积性质可以方便的求出函数(,)，且积分变换法对于其他偏微分方程例如波动方程，也是十分适用。通过MATLAB软件的模拟直观地反映了温度在介质中的变化规律，对解决实际生活中的工程问题具有指导意义。

[1]傅立叶.热的解析理论[M].桂质亮,译.北京:北京大学出版社,2008.

[2]孙桂荣,杨琰琰.二阶复域微分方程解的径向振荡[J].苏州科技大学学报(自然科学版),2018,35(02):11-14.

[3]杨琰琰,黄志刚,胡梦薇.一类非线性差分方程解的若干性质[J].苏州科技大学学报(自然科学版),2018,35(03):23-26.

[4]王畅,王翘楚,刘伟,史庆藩.数学物理方程求解中的创新思维探源[J].大学物理,2018,37(09):56-59.

[5]刘子建.一类二阶常系数非齐次线性微分方程初值问题的若干种解法[J].黑龙江科技信息,2016(34):54.

[6]樊龙,李高.利用齐次化原理求解常系数非齐次线性方程初值问题[J].大学数学,2017,33(02):111-113.

[7]朱一超.数学物理方程与进阶分析工具[M].北京:科学出版社,2020.

[8]代莹,肖冰.热传导方程中傅氏积分与傅氏变换的应用[J].新疆师范大学学报(自然科学版),2019,38(02):5-15.

[9]数学物理方程/谷超豪等编著.—3版.—北京：高等教育出版社,2012.7

[10]张景军,郭艳凤.拉普拉斯变换法求解超短脉冲方程[J].数学的实践与认识,2018,48(21):220-225.

[11]赵迎春,布仁满都拉.偏微分方程的积分变换法及其MATLAB解算[J].现代计算机(专业版),2016(29):53-55.

[12]周轩,崔虹云.电磁场中的高斯定理证明及其巧妙解题运用[J].广东化工,2019,46(21):168-169.