分枝马氏过程与超过程的中心极限定理

任艳霞，宋仁明

(1.北京大学 数学科学学院，北京 100871；2.伊利诺伊大学 数学系，厄巴纳 G1801；3. 四川大学 数学系，四川 成都 610065)

1 预备知识

1.1 模型介绍

1.1.1 分枝过程

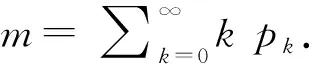
若系统中共有k类粒子，粒子类型记为{1,2,…,k}.系统中粒子死亡后可以产生不同种类的粒子，同类粒子产生的后代分布相同.令随机变量Zn(j)为第n代存活的j类粒子的总数，定义Zn= (Zn(1),Zn(2),…，Zn(j),…，Zn(k)),称{Zn,n≥1}为多物种分枝过程.令mij表示第i类粒子产生的后代中j类粒子的个数的期望，称矩阵M= (mij)1≤i,j≤k为多物种分枝过程的期望矩阵.Kolmogorov等在1947年提出了连续时间参数的分枝过程.假设每个粒子的寿命服从指数分布.对于t≥0,定义随机变量Zt：= (Zt⑴,Zt(2),…，Zt(j),…,Zt(k)),其中Zt(j)为t时刻存活的j类粒子的总数，称{Zt,t≥0} 为连续时间参数的分枝过程.期望矩阵为Mt∶=(mt(ij))1≤i,j≤k,其中mt(ij)是i类粒子经过时间t生成的j类粒子总数的期望.

1.1.2 分枝马氏过程

Ⅰ)底过程：E上的Hunt过程ξ={ξt,∏x};

令{pn(x)∶n=0,1,2,…}的母函数为

由上述3个要素，可以构造E上的分枝马氏过程.考虑如下分枝系统：

Ⅰ)系统中每个粒子u在E上运动，且出生时间和死亡时间是随机的，分别记为bu和du;

Ⅱ) 若粒子在位置x∈E出生，则它按照从x出发的ξ运动.令{zu(r)∶r∈[bu,du]}为u的运动轨道；

Ⅲ) 若粒子u在t时刻是活着的，则其在无穷小区间[t,t+dt]内存活的概率为β(zu(t))dt+0(dt);

Ⅳ) 当粒子u在位置x∈E死亡，它在x处以概率pn(x)产成n个后代，且每个后代独立的从x处开始按照上述规则运动、死亡、产生后代；

Ⅴ) 当粒子到达∂,它将从系统中消失.

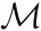
(1)

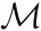
则ω(t,x)是方程

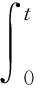
(2)

1.1.3 超过程

超过程是另一类测度值马氏过程.超过程同样由以下3要素构成.

Ⅰ) 底过程：E上的Hunt过程ξ={ξt,∏x};

Ⅲ) 分枝机制

(3)

(4)

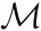
(5)

其中,uf(x,t)是下列方程的唯一的非负的局部有界解：

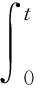
(6)

关于这类超过程的存在性及其他性质，可参见李增沪[2]和Dynkin[3].

超过程可以作为分枝马氏过程在恰当尺度变换下的极限过程，且这种构造方法可以更清楚地看出超过程3个参数(ξ,β,ψ)的具体意义.对于k≥1,设{Yk(t),t≥0}是一个参数为(ξ,γkβ,φk)的分枝马氏过程，且参数满足

1.2 分枝马氏过程和超过程的极限定理发展

分枝马氏过程和超过程也有相应的整体意义上的上临界、临界和下临界的定义.粗略说，上临界过程的灭绝概率小于1,而临界和下临界的过程在某些条件下一定会灭绝.这就导致在考虑3类模型时关心的问题完全不同.

分枝过程和超过程极限定理的研究，一直受到高度的关注.近十几年来，有很多文章讨论了上临界分枝过程和超过程的大数定律，主要包括文献[4-16].在最近的文献中，还有一些其他形式的极限定理，例如文献[17-21].

1966年，Kesten等[22-23]首次讨论了上临界多物种Galton-Watson分枝过程的中心极限定理，主要用到的工具是期望矩阵M的Jordan标准型.Athreya证明了上临界多物种连续时间分枝过程的中心极限定理，Athreya用到的主要工具是期望矩阵Mt的Jordan标准型和其特征向量[24-26]. Asmussen和Keiding在文献[27]中，用鞅的中心极限定理证明了上临界多物种分枝过程的某类中心极限定理.

设{Xt,t≥0}是一个分枝马氏过程，则对于可测函数f,随机变量〈f,Xt〉表示f关于测度Xt的积分.关于上临界分枝马氏过程,Asmussen等[28]给出了〈f,Xt〉的中心极限定理,但是，书中提出的条件不是很容易验证，书中唯一给出的满足这些条件的例子是在光滑区域上的分枝扩散过程，而且可以验证分枝Ornstein-Uhlenbeck过程不满足此条件.

本综述文章在此基础上，给出更一般的分枝马氏过程和超过程的系列中心极限定理.首先提出了1个好的框架，它包含了很多常见的过程，同时文中提出的假设比较容易验证，弥补了之前文章的一些不足.另一方面，相比之前文章的结果更优，得到了一些全新的结论.最后，本文提出的假设适用于非对称情形，在处理非对称情形时给出了关于非对称紧算子谱理论的一些结果，非对称情形的结果较复杂[40].

2 关于底过程的假设和性质

2.1 基本符号

•Lp(E,m;)(Lp(E,m)),p≥1:关于测度m的p-阶矩有限的可测复(实)函数全体.当p<∞,‖f‖p:=当p=∞,‖f‖∞为f关于测度m的本质上确界.

•〈·,·〉m:希尔伯特空间L2(E,m)和L2(E,m;)上的内积.

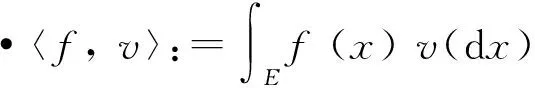
2.2 基本假设和性质

给出本文中所讨论的分枝马氏过程和超过程的底过程满足的假设条件及一些常用的性质.

用{Pt:t≥0}表示底过程ξ的半群.全文中考虑底过程ξ={ξt,∏x}都满足以下条件.存在一族定义在E×E上连续的严格正的函数{p(t,x,y) :t>0}满足：

定义

(7)

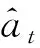
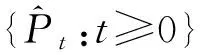
(8)

因此

(9)

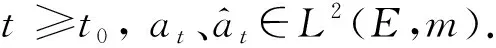
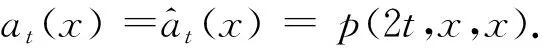
设a∈ßb(E),定义Feynman-Kac半群{Tt,t>0},

注意对于分枝马氏过程和超过程，它们的期望公式跟Tt有相同的形式，都是底过程半群的Feynman-Kac变换，是对应的α的表达式不同.下面介绍一个非常有用的引理, 其证明参见文献[4].

引理2假设1a)、b)成立.则半群{Tt:t≥0}存在转移密度q(t,x,y),使得

e-‖α‖∞tp(t,x,y) ≤q(t,x,y)≤e‖α‖∞tp(t,x,y),(t,x,y)∈(0,∞)×E×E.

(10)

并且对于任意t>0,q(t,x,y)关于(x,y)是连续的.特别地，当p(t,x,y)=p(t,y,x)时,q(t,x,y)=q(t,y,x).

(11)

定义

(12)

(13)

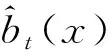
对任意的t>0及f∈L2(E,m;),Ttf是连续的.事实上，由于q(t,x,y)是连续的, 由式(13)和假设1中b),根据控制收敛定理可得Ttf是连续的.

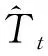
2.3 满足假设1的对称马氏过程的例子

本小节将给出一些满足假设1的对称马氏过程的例子.这些例子说明有很多马氏过程是满足这些条件的.下面的第1个例子包含了 Ornstein-Uhlenbeck过程(简称OU过程).

例1 (隶属 Ornstein-Uhlenbeck过程).令σ、b>0 是2个常数.η={ηt:t≥0}是一 个d上的OU过程，它是一个扩散过程，无穷小生成元为

对任意x∈d,用∏x表示初始值为x的过程ξ的分布.已知在概率∏x下,ηt～其中并且η有一个不变密度为

令

则

(14)

令E=d,m(dx) =μ(x)dx,则ηt关于测度m的密度函数为

特别地，

取t0>0使得4/(e2abt0+1) <1.根据Hölder不等式，有

当t≥2at0,有

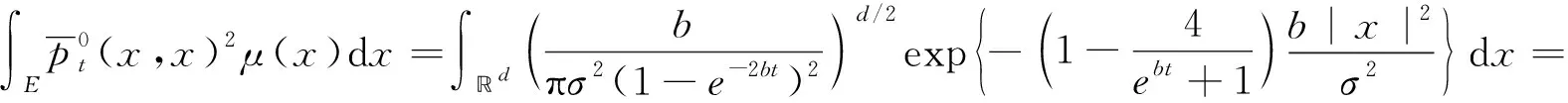
从而

因此,过程ξ满足上一小节中提出的所有假设条件.

例2 设V是d上的非负的局部有界的函数，满足：存在R>0,M≥1使得，对所有的|x| >R,

M-1(1+V(x))≤V(y)≤M(1+V(x)),y∈B(x,1),

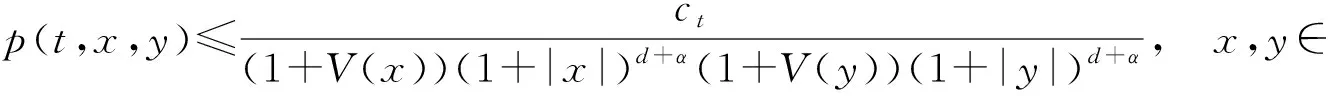
取E=d,m是d上的勒贝格测度，由上面的不等式，容易验证ξ满足上一小节中提出的所有假设条件.

例3L:[0,∞)→[0,∞)是单调不减的函数，如果limt→∞L(t) =∞且存在c>1使得

L(t+ 1) ≤c(1 +L(t)),t≥0,

则称L∈L.设V是d上的非负函数，满足且存在L∈L,C>0使得对所有x∈d,L(|x|) ≤V(x)≤C(1+L(|x|).设m0>0,α∈(0,2)是常数,令ξ是d上的马氏过程，无穷小生成元为用p(t,x,y)表示ξ关于勒贝格测度的密度函数.根据文献[43],对于t>0,存在ct>0使得

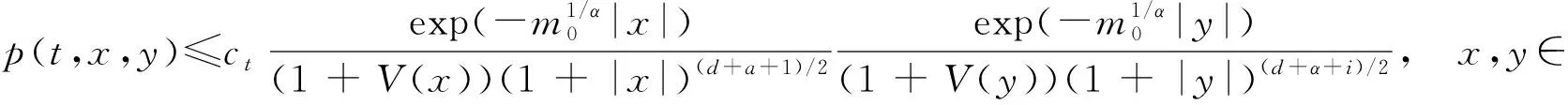
取E=d,m是d上的勒贝格测度，容易验证ξ满足上一小节中提出的所有假设条件.

例4 设E是局部紧的可分距离空间，m是E上的有限Borel测度且支撑为E.ξ= {ξ,∏x}是一个m-对称的Hunt过程.设对于t>0,ξt存在连续的，对称的，严格正的密度函数p(t,x,y).如果ξ的半群是超压缩的，即，对t>0,存在ct>0使得

p(t,x,y)≤ct, (x,y)∈E×E,

则容易得到ξ满足上一小节中提出的所有假设条件.

下面是一些满足超压缩条件的例子：

1) 设D是d上的连通开集，具有有限测度，m是D上勒贝格测度.对d上的扩散过程，若其无穷小生成元为一致椭圆扩散型二阶微分算子，则它在区域D中带斩杀 边界的子过程满足本例中的所有条件.

2) 设D是d上有界连通的C2开集，m是D上勒贝格测度.则中的反射布朗运动满足本例第1段中的条件.

3) 设D是d上的开集，具有有限测度，m是D上勒贝格测度.则对于任意隶属布朗运动在D中带斩杀边界的子过程满足本例第1段中的条件，详细可参见文献[44-45].

3 上临界分枝对称马氏过程的中心极限定理

讨论上临界分枝对称马氏过程的中心极限定理.本节考虑的分枝过程的底过程ξ={ξ,∏x}满足上一节中的假设1,并且要求p(t,x,y)=p(t,y,x) (即ξ={ξ,∏x}是m-对称的)，分枝律满足二阶矩条件

(15)

定义

(16)

和

(17)

由式(15)知，存在K>0,使得

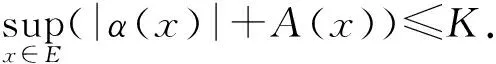
(18)

过程X的一阶矩公式：对于f∈ßb(E)及(t,x)∈(0,∞)×E,

(19)

(20)

(21)

式(21)中的级数是在E×E上局部一致收敛的.上述结论的证明，参见文献[46].主要讨论上临界分枝马氏过程，即假设2.

假设2λ1<0.

对于任意的f∈L2(E,m),有下面的展开：

(22)

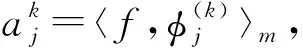
这里使用惯例infφ=∞.定义

若f∈L2(E,m)是非负的且m(x∶f(x) >0)>0,则〈f,φ1〉m>0,即γ(f) =1,且易得f*(x)=a1φ1(x)=〈f,φ1〉mφ1(x).在本节的主要结论中将用到下面3个L2(E,m)中的子函数类：

(23)

(24)

(25)

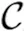
3.1 大数定律

在考虑中心极限定理之前，先来叙述大数定律.定义

(26)

首先给出一个重要的引理.

(27)

存在.

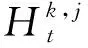
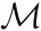
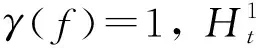
注意在定理1中，要求f∈L2(E,m)∩L4(E,m).但是接下来的结果表明，对于非负的f,是可以去掉f∈L4(E,m)这一条件的.

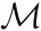
(28)

3.2 中心极限定理

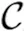
(29)

和

(30)

(31)

和

(32)

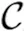
(33)

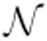
定义

及

f(l)(x)∶=f(x)-f(s)(x)-f(c)(x).

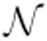
4 上临界分枝非对称马氏过程的中心极限定理

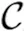
5 上临界超过程的中心极限定理和泛函中心极限定理

5.1 假设条件

这一节将开始讨论上临界超过程的中心极限定理.这里只讨论底过程是对称的情形.事实上，可以得到底过程非对称情形的结果.本节讨论的超过程的3要素(ξ,β,ψ)满足的条件如下.

3)分枝机制ψ的形式如式(3),且满足

(34)

第2.3节中已经给出了很多满足上述假设的底过程的例子，这里不再重复.定义

(35)

注意，此处α、A与分枝马氏过程的α和A(见定义(16), (17))不同，但由于它们的作用是相似的，由于不会产生混淆，使用了相同的记号.根据假设α(x)∈ßb(E),A(x)∈ßb(E)知存在常数K>0使得

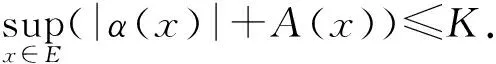
(36)

超过程X的一阶矩公式为：对于任意的f∈ßb(E),

(37)

只讨论上临界超过程，即假设3.

假设3

λ1<0.

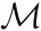
本节中，主要工具是超过程的游弋测度，因此进一步需要下面的假设条件来保证游弋测度的存在性并使其满足一些好的性质.

假设4对任意的t>0,x∈E,

(38)

首先将给出一个满足假设4的充分条件.这个充分条件只针对分枝机制ψ，因此与假设1不冲突.

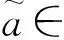
(39)

在假设4下，将给出超过程X的中心极限定理.对任意的f∈L2(E,m),以下展开式成立：

(40)

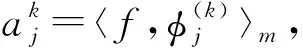
这里令infφ=∞当且仅当f=0,m-a.e.令

5.2 大数定律

先给出大数定律，这些结论与第3节的大数定律相似，证明方法也相似.定义

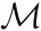
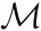
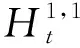
下面将给出另一个弱大数律，在本推论中，将去掉f∈L4(E,m)这个假设.

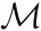
(41)

5.3 中心极限定理

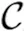
(42)

(43)

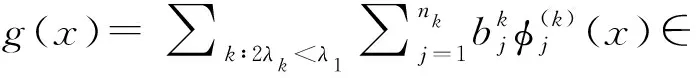
(44)

同时定义随机变量

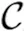
(45)

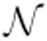
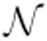
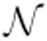
5.4 泛函中心极限定理

5.3节给出了上临界超过程的中心极限定理，本节将进一步给出更强的结果——泛函中心极限定理.5.4节是5.3节结果的继续，假设条件完全相同，这里不再重复.

给定q>max{K, -2λ1}.对任意的p≥1和f∈Lp(E,m),定义

(46)

即Uq|f|∈Lp(E,m).令f+和f-分别表示f的正部和负部.对于x∈E,若Uq|f|(x)<∞,定义

否则定义Uqf(x)为任意一实数.根据式(46),Uq是Lp(E,m)上的有限线性算子.注意

容易验证对于f∈L2(E,m),γ(Uqf) =γ(f).事实上由Fubini定理，有

(47)

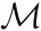
在这个意义下，可以考虑〈Uqf,X.〉作为轨道值随机变量的极限.

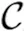
(48)

(49)

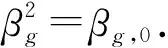
(50)

(51)

E(G1,Uqf(τ1)G1,Uqf(τ2))=σUqf,τ2-τ1,0≤τ1≤τ2,

(52)

E(G3,g(τ1)G3,g(τ2))=βg,τ2-τ1,若0≤τ1≤τ2,

(53)

且

(54)

并且W∞，G2，h和(G1,Uqf,G3,g)相互独立.

对于f∈L2(E,m),参见推论1前的定义.

注6 设f∈L2(E,m)∩L4(E,m)满足λ1≥2λγ(f).令g=Uqf，则g(l)=Uqf(l),g(c)=Uqf(c)且g(s)=Uqf(s).特别地，若λ1=2λγ(f)则g(s)=0.

若f(c)=0,则g=g(l)+g(s),因此

(55)

其中G1,g(l)+G3,g(s)是一个连续的高斯过程，期望为0,协方差函数为

E[(G1，g(I)(τ1)+G3，g(s)(τ1))(G1，g(l)(τ2)+G3，g(s)(τ2))]=
σg(l),τ2-τ1+ητ1,τ2(g(l),g(s))+βg(s),τ2-τ1,0≤τ1≤τ2.

若f(c)≠0,则

根据式(55)，有

因此根据定理7中极限的第1个和第3个分量的结果，有

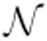
6 稳定分枝机制上临界超Ornatein-Uhlenbeck的中心极限定理

本节考虑二阶矩不存在情形的超Ornstein-Uhlenbeck过程(超OU过程)X的中心极限定理.底过程为ξ={(ξt)t≥0;(∏x)x∈d}为d中取值的Ornstein-Uhlenbeck过程(OU过程)的情形，ξ的生成元为

(56)

其中σ>0与b>0是常数.考虑分枝机制ψ是空间齐次的情形，即

(57)

近期Marks等[48]建立了具有特殊稳定分枝机制(二阶矩不存在)的上临界分枝OU过程的空间中心极限定理，在文献[49-50]中，建立了二阶矩不存在情形的超OU 过程X的中心极限定理，其中分枝机制ψ满足下面2个条件：

假设6假设存在η>0及β∈(0,1)使得

(58)

对δ>0成立.

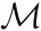
与前面相同，用(Pt)t≥0表示ξ的转移半群.对x∈d,t≥0及f∈ß+(d), 定义∏x[eαtf(ξt)].对任意μ∈(d),t≥0及过程ξ在d上具有不变概率：

(59)

令L2(φ)表示内积为

(60)

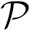
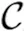
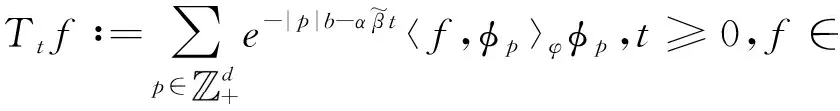
(61)

及

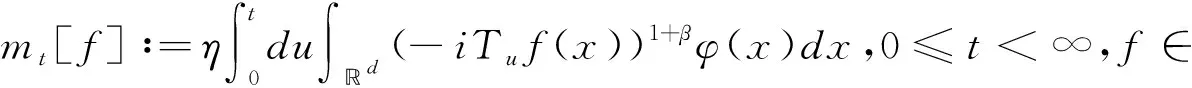
(62)

文献[49]证明了如下结果：

对任意f∈,存在特征函数为θem[θf],θ∈的(1+β)-稳定随机变量ζf,这里

(63)

定义

(64)

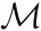
(65)

作为上面定理的推论，对任意f∈,有下面关于Xt(f)的中心极限定理.

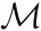
1)如果fc≡0,则

这里ζfs与ζ-fl是由式(63)刻画的(1+β)-稳定随机变量，ζfs与ζ-fl相互独立；

2)如果fc≢0,则

这里ζfc是由式(63)刻画的(1+β)-稳定随机变量.

注7 本节中考虑的分枝机制是空间齐次的，很自然进一步地研究应该考虑更一般的空间非齐次且二阶矩不存在情形的中心极限定理.