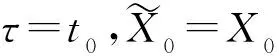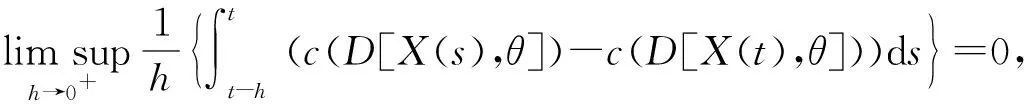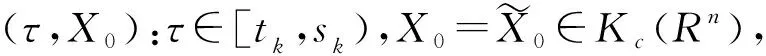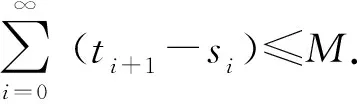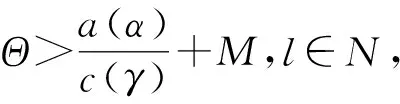具有非瞬时脉冲影响的集值微分方程解的稳定性

2021-10-22王培光郭梦煜鲍俊艳

河北大学学报（自然科学版） 2021年5期

王培光,郭梦煜,鲍俊艳

( 河北大学数学与信息科学学院, 河北保定 071002)

近年来,脉冲微分方程理论已成为微分方程的一个重要的研究领域.脉冲根据作用时间长短可以分为瞬时脉冲和非瞬时脉冲,其中非瞬时脉冲是指干扰过程依赖于状态且持续作用一段时间.在现实生活中,非瞬时脉冲现象普遍存在,其在药物动力学、种群生态动力学、传染病动力学等方面已有广泛应用.20世纪60年代,Millman等[1-2]首次提出瞬时脉冲微分方程.非瞬时脉冲微分方程的研究发展相对滞后.2012年,首先由Hernandez等[3]提出,并研究了其弱解和经典解的存在性.关于非瞬时脉冲微分方程理论及应用研究刚刚起步,就迅速受到国内外专家学者的关注,基本结果可参见文献[4-8].

集值微分方程是描述不确定系统的有效工具,在控制科学、生物、计算机与信息处理等领域有着重要应用.其显著特征是当集值映射为单值映射时,集值微分方程的Hukuhara导数和积分可以归结为普通向量的导数和积分,在该框架下得到的结果是常微分方程的相应结果.Pinto等[9]在1969年首先给出了集值微分方程解的存在性、唯一性等基本结果.关于集值微分方程的系统工作参见文献[10].关于脉冲集值微分方程解的稳定性的相关工作参见文献[11-13].

本文讨论具有非瞬时脉冲集值微分方程,利用比较原理及Lyapunov函数方法研究其解的稳定性问题,给出该类方程解的稳定性、一致稳定性、一致渐近稳定性的判别准则.

1 预备知识

设Kc(Rn)是由Rn上所有非空、紧致凸子集构成的集合.A,B∈Kc(Rn),A与B的Hausdorff度量表示为

(1)

其中,d(x,A)=inf{d(x,y):y∈A}.特别地,

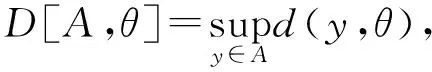
(2)

其中,θ是Kc(Rn)的零元素.

空间Kc(Rn)的加法和标量乘法的自然代数运算定义如下[10]：

A+B={y+x:y∈A,x∈B},λA={λy:y∈A},

其中,A,B∈Kc(Rn),λ∈R+.则Kc(Rn)可以作为完备锥嵌入到相应的Banach空间中,由此构成半线性度量空间.

Hausdorff度量式(1)满足如下性质:

D[A+C,B+C]=D[A,B],
D[A,B]=D[B,A],
D[A,B]≤D[A,C]+D[C,B],
D[λA,λB]=λD[A,B],

其中,A,B,C∈Kc(Rn),λ∈R+.

给定任意集合A,B∈Kc(Rn),如果存在集合C∈Kc(Rn),满足A=B+C, 则称C为A与B的Hukuhara差集,记为A-B.

定义2设F:I→Kc(Rn)在I上是Hukuhara可积的,S(F)表示F在I上所有可积的选择所组成的集合,则F在I上的Hukuhara积分表示为

若F:I→Kc(Rn)在I上是Hukuhara可积的,则下列性质成立:

若F,G:I→Kc(Rn)可积,则D[F(·),G(·)]:I→R也是可积的,且

(3)

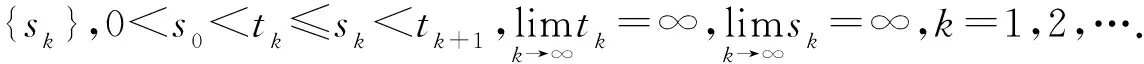
考虑具有非瞬时脉冲集值微分方程(NISDE)

(4)

NISDE (4) 的非平凡解可由下式给出

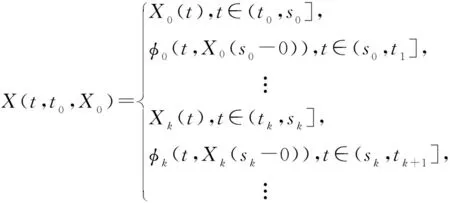
(5)

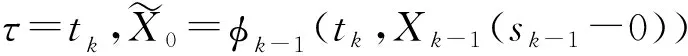
2 主要结果

为方便起见,给出如下所需函数类:

K={c∈C[R+,R+]:c是严格单调递增的，c(0)=0},

S(ρ)={X∈Kc(Rn):D[X,θ]≤ρ,ρ>0是常数}.

令T>t0, 使得sp-1

另外,当T=∞时,[t0,T]变为[t0,∞).

下面引入类Λ的Lyapunov函数.

定义3令J⊂R+,Δ⊂Kc(Rn),其中θ∈Δ.称函数V(t,X):J×Δ→R+属于类Λ(J,Δ),其中V(t,θ)≡0,若

定义4函数V(t,X)∈Λ(J,Δ)的广义Dini导数为

其中,X∈Δ, 对于任意的t∈(tk,sk),存在ht>0,使得当0

(6)

其中,t0>0,J⊂R+,Δ⊂Kc(Rn).则函数V(t,X(t))在J上关于t是单调非增的,即V(t,X(t))≤V(t0,X0),t∈J成立.

引理1的证明与文献[14]中的命题 1.3.1的证明类似,在此略去.

引理2假设下列条件成立:

A2)存在函数V∈Λ([t0,T],Δ)使得

②对于任意的k=0,1,2,…，

V(t,X(t))≤V(sk-0,X(sk-0)),t∈(t0,T]∩(sk,tk+1].

则V(t,X(t))≤V(t0,X0)在[t0,T]上成立.

证明:不失一般性,假设t0∈[0,s0),T=sp.令t∈[t0,s0].当p=1时,由引理2条件A1)、A2)中①和引理1,有V(t,X(t))≤V(t0,X0).

令t∈(s0,t1].由引理2条件A1)、A2)中②和引理1,有

V(t,X(t))≤V(s0-0,X(s0-0))=V(s0,X(s0))≤V(t0,X0).

令t∈(t1,s1].当p=2时,由引理2条件A1)、A2)中①和引理1,得到

V(t,X(t))≤V(t1,X(t1))≤V(t0,X0).

重复上述过程,由归纳法知,当t∈[t0,T]时,结论得证.

注1 当p=∞时,[t0,T]变成[t0,∞),引理2也是成立的.

定理1假设A1)成立,且

A3)存在函数V∈Λ([t0,T],Δ)使得

②V(t,X(t))≤V(sk-0,X(sk-0)),t∈[t0,T]∩(sk,tk+1],k=0,1,2，….

则当t∈[t0,T]时,

令t∈(s0,t1].由条件A3)中②,可得

令t∈(t1,s1].当p=2时,由条件A3)中①,得到

重复上述过程,由归纳法知,当t∈[t0,T]时,结论得证.

令X(t,t0,X0)∈PC1([t0,∞),Kc(Rn))表示NISDE(4)的任意解.下面给出具有非瞬时脉冲集值微分方程平凡解的稳定性的定义.

定义5NISDE(4)的平凡解X(t,t0,X0)是

S4)一致渐近稳定的,如果S2)和S3)同时成立.

为给出稳定性结果, 首先给出下列所需条件:

B2)函数φk∈C((sk,tk+1]×Kc(Rn),Kc(Rn)),对于任意Y∈Kc(Rn)和t∈(sk,tk+1],至少存在一个函数Z:(sk,tk+1]×Kc(Rn)→Kc(Rn),使得Z(t,X)=φk(t,X),Z(t,θ)≡θ.

定理2假设B1)、B2) 成立,且

B3)存在函数V∈Λ(R+,Kc(Rn))使得

②V(t,φk(t,X))≤V(sk-0,X),t∈(sk,tk+1],X∈Kc(Rn),k=0,1,2，…;

③b(D[X,θ])≤V(t,X),t∈R+,X∈Kc(Rn),其中b∈K.

则 NISDE(4) 的平凡解是稳定的.

由V(t,X)连续,V(t0,θ)=0,则存在δ1=δ1(t0,ε)且0<δ1≤ε,使得当D[X0,θ]<δ1时, 有V(t0,X0)

即满足引理2的条件A2)中①, 其中T=∞,Δ=Kc(Rn).

令t∈(sk,tk+1],k=0,1,2,…，由条件B3)中②, 可得

V(t,X(t))=V(t,φk(t,X(sk-0)))≤V(sk-0,X(sk-0)).

因此, 也满足引理2的条件A2)中②.由注1、条件B4)中③和X0的选择, 得到

b(D[X(t),θ])≤V(t,X(t))≤V(t0,X0)

故NISDE(4) 的平凡解是稳定的.

定理3假设B1)、B2)成立, 且

B4) 存在函数V∈Λ(R+,Kc(Rn))使得

②V(t,φk(t,X))≤V(sk-0,X),t∈(sk,tk+1],X∈S(ρ),k=0,1,2,…;

③b(D[X,θ])≤V(t,X)≤a(D[X,θ]),t∈R+,X∈Kc(Rn),其中a,b∈K,

则NISDE(4) 的平凡解是一致稳定的.

D[X(t),θ]<ε,t≥t0.

(7)

假设式(7)不成立,则存在t*>t0,使得D[X(t*),θ]=ε,并且当t∈[t0,t*)时,D[X(t),θ]<ε,当t∈(t*,t*+δ)时,D[X(t),θ]≥ε,其中δ>0充分小.下面分2种情况进行证明.

情况Ⅰt*≠sk,k=0,1,2,….则当t∈[t0,t*]时,有X(t)∈S(ρ).根据条件B4)及引理2,由T=t*,Δ=S(ρ),得到当t∈[t0,t*]时,有V(t,X(t))≤V(t0,X0).由条件B4)中③和X0的选择,可得

b(D[X(t*),θ])≤V(t*,X(t*))≤V(t0,X0)≤a(D[X0,θ])

因此,有D[X(t*),θ]

情况Ⅱ 存在自然数p<∞,使得t*=sp.对于t∈[t0,t*],有X(t)∈S(ρ),根据引理2,由T=sp,Δ=S(ρ),得到当t∈[t0,sp]时,有V(t,X(t))≤V(t0,X0).由条件B4)中②,可得当t∈(sp,tp+1]时,V(t,X(t))=V(t,φp(t,X(sp-0)))≤V(sp-0,X(sp-0)).

因此,由条件B4)中③和X0的选择,得到当t∈(sp,tp+1]时,

b(D[X(t),θ])≤V(t,X(t))≤V(sp-0,X(sp-0))≤V(t0,X0)≤a(D[X0,θ])<δ1.

又由δ1的选择,当t∈(sp,tp+1]时,D[X(t),θ]

定理4假设B1)、B2)成立,且