Stampacchia引理、推广及应用

高红亚， 高斯宇

(1.河北大学 数学与信息科学学院,河北省机器学习与计算智能重点实验室，河北 保定 071002；2.北德克萨斯大学 数学系，德克萨斯州 丹顿 76203)

1 Stampacchia引理

1.1 经典的Stampacchia引理

Stampacchia引理，又称De Giorgi-Stampacchia引理，是De Girogi和Stampacchia在研究偏微分方程解的正则性时引入的，目前已经成为现代偏微分方程正则性理论中的1个重要的工具.这个引理第1次出现在文献[1]中，但形式不完整.第1个完整的形式出现在文献[2]中.

Stampacchia引理[2]设c1,α,β为正常数，k0为实数.设函数φ:[k0,+∞)→[0,+∞),非增，且对任意的h>k≥k0有

(1)

Ⅰ) 若β>1，则φ(k0+d)=0,其中常数d满足

(2)

Ⅱ) 若β=1，则任意k≥k0有

(3)

Ⅲ) 若β<1且k0>0，则任意k≥k0有

(4)

Stampacchia引理在椭圆型偏微分方程的正则性理论以及变分问题中有广泛的应用.举一个简单的例子，见文献[3],考虑散度型椭圆方程的边值问题

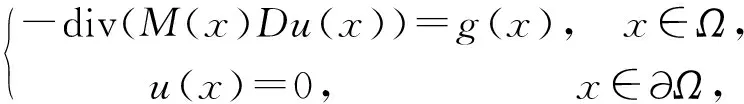
(5)

其中Ω⊂RN,N>2,

(6)

M(x):Ω→RN×N为满足下面条件的矩阵：存在0<α≤β<∞，使得

〈M(x)ξ,ξ〉≥α|ξ|2,|M(x)|≤β,a.e.Ω.

(7)

Gk(u)=u-Tk(u)=u-min{1,k/|u|}u.

作为式(5)中的实验函数，并利用式(7)得

利用Hölder不等式和Sobolev嵌入不等式，有∀h>k≥0，

其中

Ak={x∈Ω:|u(x)|>k}

为u的超水平集，|Ak|为Ak的Lebesgue测度，cg为与g(x)有关的常数.于是式(1)对

成立.利用Stampacchia引理得到

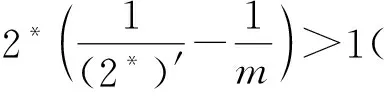
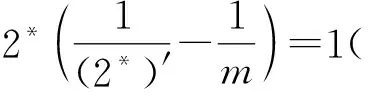
上述例子说明了如何应用Stampacchia引理推导出正则性结果.与Stampacchia引理相关的结果，参见文献[4-16].

1.2 2个条件的比较

式(1)中取h=2k，变成

(8)

需要说明的是，一些问题的推导直接得出式(8)，例如文献[14]中，Kovalevsky, Voitovich给出了下面的结果：

命题1设c3,α,β,k0为正常数，函数φ∶[k0,+∞)→[0,+∞)非增，且对任意的k≥k0，有

则对任意k≥k0有

形式上看，式(8)比式(1)要弱.但对β的不同取值情况不一样.在文献[11]，比较了式(8)和式(1)，得到：

命题2Ⅰ)当0<β<1时，式(1)和式(8)等价;

Ⅱ)当β=1时，式(1)比式(8)强，且函数φ(k)=e(ln k)2,k∈[1,+∞]满足β=1,α=2ln 2,c3=2-ln 2时的式(8)，但对任意常数α>0,c1>0不满足式(1)；

Ⅲ) 当β>1时，式(1)比式(8)强，且函数φ(k)=e-kp,p=log2(2β),k∈[1,+∞),满足β>1,c3=1,任意α>0和对某k0=k0(α,β)≥1的式(8)，但对任意β>1，α>0，c1>0,不满足式(1).

2 经典Stampacchia引理的推广

虽然经典的Stampacchia引理应用广泛，但在一些更广泛问题的研究中却不再适用，因此有推广的必要.

文献[14]中，Kovalevskii和Voitovich在研究四阶方程时，给出了Stampacchia引理的几个推广，见文献[14]中的引理2-4.文献[17]中，给出了稍微不同的结果，且证明更初等.下面的引理来自文献[17].

命题3设c4、α、β、k0为正常数，0≤θ<1.设φ：[k0,+∞)→[0，∞)非增，且对任意h>k≥k0满足

(9)

Ⅰ)若0<β<1，则任意k≥k0，有

Ⅱ)若β=1，则对任意k≥k0，有

Ⅲ)若β>1，则存在k*>0使得φ(k*)=0.

在研究方程组时，会遇到下面的条件，即式(1)变成对任意h>k≥k0，

(10)

其中，N>1为方程组中方程的个数.文献[18]的引理1.2将Stampacchia引理进行了以下推广：

命题4设c5，α，β，k0为正常数，N>1.设φ：[k0,+∞)→[0,+∞)非增，且对任意h>k≥k0满足式(10).

Ⅰ)若0<β<1，则任意k≥k0，有

其中

其中

3 1个应用

为了说明推广的Stampacchia引理的应用，本文给出一个例子.考虑如下的退缩椭圆型偏微分方程的边值问题

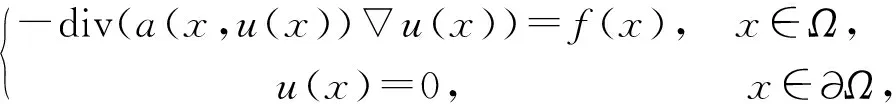
(11)

其中,Ω⊂RN(N>2)为有界区域，函数a(x,s)∶Ω×R→R为满足下列条件的Carathéodory函数：存在0<α≤β<+∞和0≤θ<1使得

(12)

而

f(x)∈Lm(Ω),(2*)′≤m<∞.

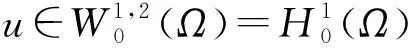
(13)

Boccardo等在文献[5]的第14章对问题(11)进行了研究也见文献[19]，得到如下结果：

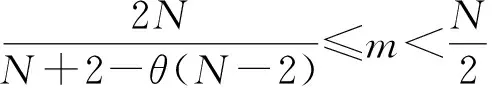
Tk(u)=max{-k,min{k,u}}

为函数u在k>0水平上的截断.取

φ=Gk(u)=u-Tk(u)

为式(13)中的实验函数，并注意到在集合{x∈Ω:|u(x)|≤k}上φ=0，得到

(14)

其中

Ak={x∈Ω:|u(x)|>k}.

由此推出

(15)

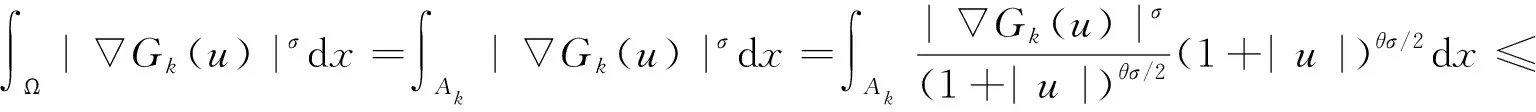
(16)

估计上式两端.式(16)左端由Sobolev嵌入定理

可得

(17)

式(16)右端第3项由

和

(a+b)p≤2p(ap+bp),a,b>0,p>0，

推出当k≥1时，

(18)

联合式(16)、式(17)、式(18)得到，当k≥1时,

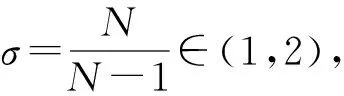
(19)

(20)

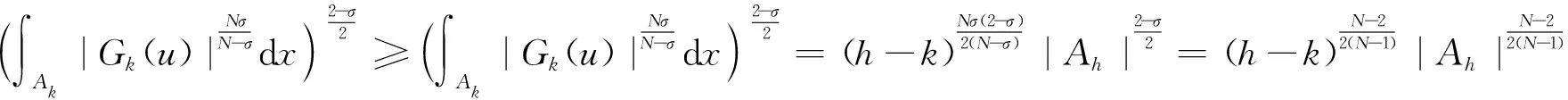
(21)

联合式(20)、式(21)得到

由此得

其中τ为与N、θ、α、‖f‖LN/2(Ω)有关的常数，如命题3的Ⅱ)所示，而2λ=τθ-1,c12=|Ω|e1+2λ.由上式有

|{eλ|u|1-θ>eλk1-θ}|=|{|u|>k}|≤c12e-2λk1-θ.

利用文献[5]中引理3.11，即f∈Lr(Ω)(r≥1)的充要条件是

所以eλ|u|1-θ∈L1(Ω).证毕.