梯度折射率介质下的光路计算与成像研究

宋 月，陈欣雨，杨锐涵，吴宇豪，程 才，刘 科

(四川师范大学 物理与电子工程学院，四川 成都 610101)

海市蜃楼是一种由于光的折射和全反射形成的自然现象。由于大气密度在垂直方向上存在梯度，物体反射的光在空气中发生多次折射和全反射，人眼沿着光路的反向切向延长线便会看到远处实物形成的“蜃景”虚像.在实验室条件下，可以使用激光照射与大气具有相似折射率梯度(指数或线性关系[1])的溶液使光路轨迹弯曲，来模拟海市蜃楼现象并定量解释其形成原理。TLopez-Arias[2]给出了非线性折射率介质下的光路方程，C.Gaffney[3]等人给出了测定折射率随高度变化的实验方案，王忠纯[4]用线性折射率模型解释海市蜃楼，黄思瑜[5]等依据费马原理和拉氏方程推导了光路轨迹方程。陈培杰，李宗民提供了新的实验方案[6，7]；Young Andrew，Diego Gutierrez介绍了大气中的蜃景[8，9]，指出大气中蜃景给航海和沙漠行人造成的距离判断的困扰。早期研究者们的工作主要集中于光路轨迹的推导与成像的定性演示，理论推导的光路轨迹还未与实验进行有效的匹配，也缺乏成像的理论计算。本文则通过自制的实验仪器(激光入射装置、溶液采样装置、自动化输液装置)，探究了溶质分子在溶液中扩散形成的折射率梯度，推导出激光在溶液中的光路方程。理论和实验的光路轨迹基本一致，并基于光路轨迹用Matlab计算成像，给出了在本实验条件下成像的偏移量与光路轨迹的传输距离的比值为0.036 6。研究结果为估算海面上空的蜃景距实景的距离提供了有效参考，同时也为教学演示海市蜃楼现象提供了新的思路和方向。

1 理论模型

1.1 光路推导—非线性折射率梯度部分

如图1(a)建坐标系，缸长为z轴，左壁为y轴：将溶液按高度细分成无限多层，每一层溶液的折射率近似看作不变，表示该角度所处层的折射率，τ为常数。

由折射定律：n(θ)·sin(θ)=n(θ1)·sin(θ1)=τ

即可将折射率与入射角的关系简化为：

(1)

对该式微分并代入，得到：

(2)

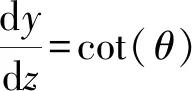
(3)

即：

y″(z)·n(y)-n′(y)[1+(y′(z))2]=0

(4)

(5)

找到n′(y)与n(y)后，由n(y=0)=n，n(y=h0)=n水，代入Mathematica NDsolve数值求解，则可得到光路轨迹的数值解。

(a)光线在缸内传输示意图

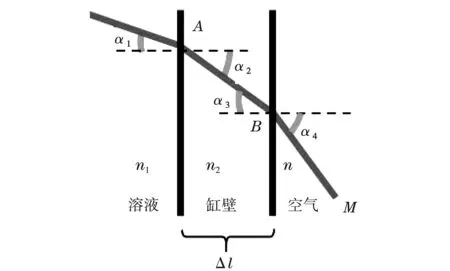
(b)光线穿出缸壁示意图图1 光路推导示意图

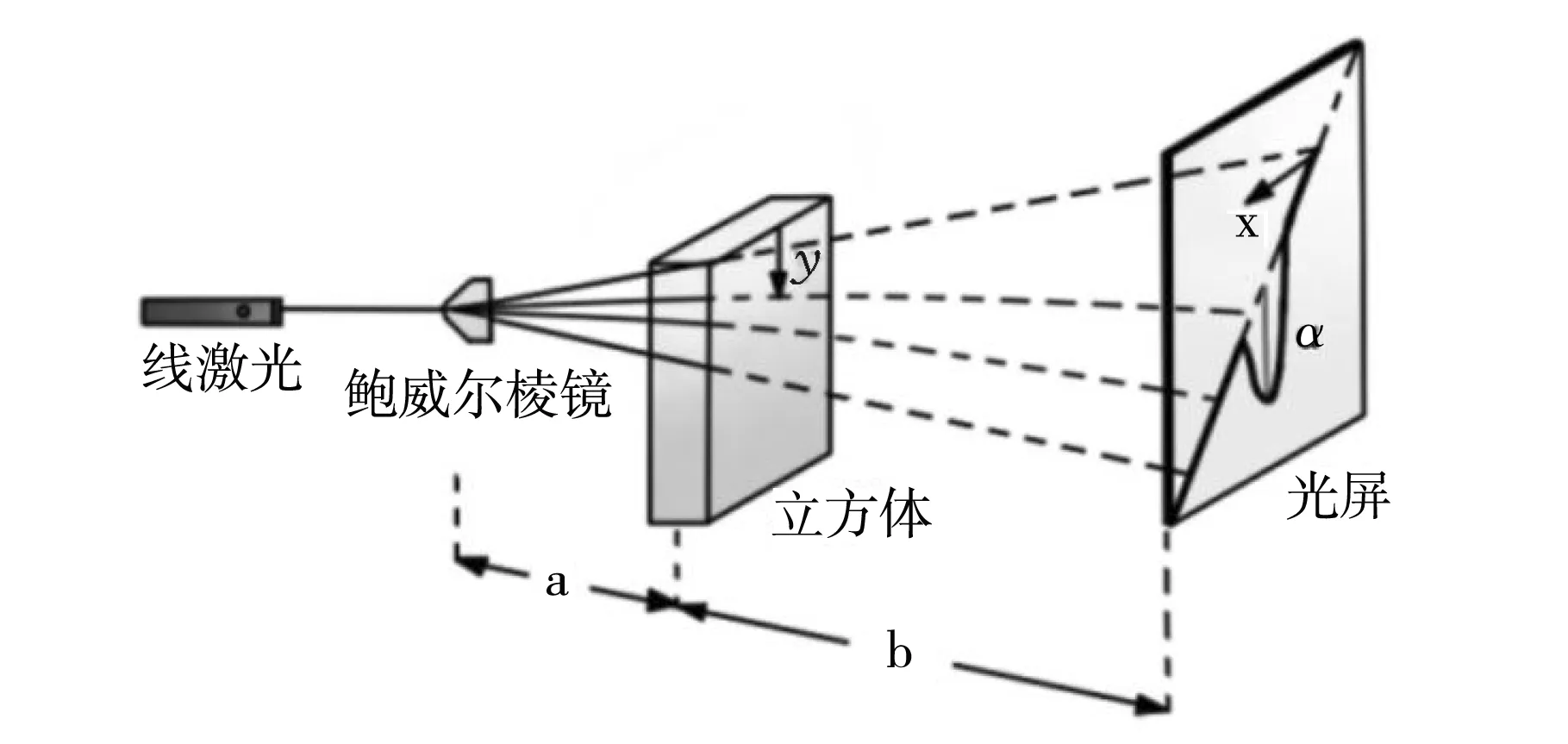
图2 随高度的变化率测量图

1.2 光路推导—线性折射率梯度部分

如图1各参量如下：n0为底层溶液折射率，α为入射光线与水平面的夹角。通常的折射率的值都是相对于钠黄光(λ=560 nm)[10]而言，针对实际激光的不同波长值，n0需做出以下修正：

再由图1中的几何关系及折射定律

nsinθ=n0sinθ1

(6)

(ds)2=(dz)2+(dy)2

(7)

(8)

联立(6)、(7)、(8)得到方程(9)

(9)

对(9)两边二阶求导

(10)

假设静置一段时间后溶液折射率满足：

n=n0(1-ky)

(11)

两边平方并求导得到

(12)

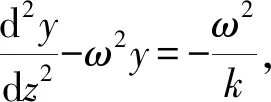
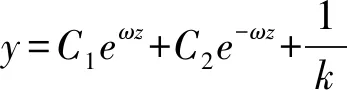
(13)

在实际光路传播过程中，光线射出经过缸壁如图1(b)，现对缸壁造成的光线偏移进行修正，设各参量如下：Δl缸的厚度，l缸总长度，n空气空气折射率，n2缸壁折射率，α1前壁入射角，α2前壁折射角，α3后壁入射角，α4后壁折射角。写出A点坐标(l,y(l))，在A点处于溶液与前壁的交界面上，由折射定律得：

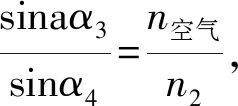
(14)

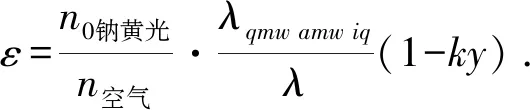
2 实验装置设计

在实验中，设计了激光入射装置以便灵活地调整激光的入射角度α和高度，自动化输液装置用水泵将液体抽送至缸底以保证每次配置的溶液初始状态基本一致。研究光路轨迹需要对不同高度层的溶液的折射率进行分析，设计了自动化溶液采样装置，用三脚架搭配万能夹来稳定搭载嵌有9个针管的亚克力板，在每个针管内装有电热丝，外接电源对针管内部进行加热，利用压强差自动吸取溶液实现在溶液同一平面进行采样的目的。

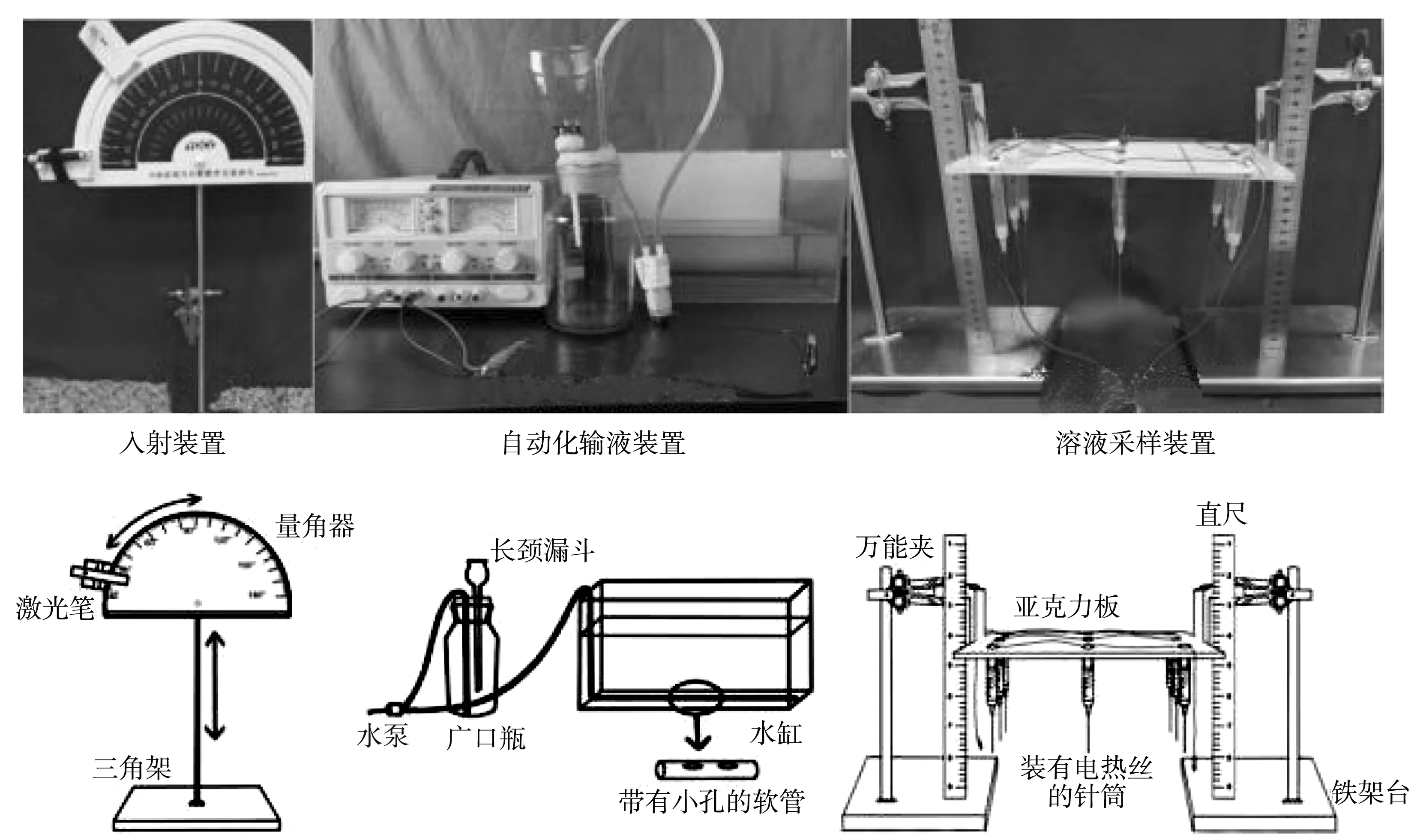
图3 实验装置实物图(上)和示意图(下)

3 实验与数据采集计算

3.1 非线性折射率梯度溶液下的成像

以盐为溶质，清水为溶剂，先在缸中倒入2 500 mL清水，用输液装置将2 500 mL浓度为10.7%的盐溶液输入缸底，在0～12 h内，溶液呈现非线性的折射率分布，光路发生较大幅度偏折，成像效果如图4，校徽下半部分拉伸，中间挤压，两侧向内突出。产生了类似于“扭曲”的蜃景。

(a)实际成像

(b)理论成像图4 盐溶液成像效果图

3.2 线性折射率梯度溶液下的光路及成像

分别以糖，盐为溶质，每层500 mL清水为溶剂以表1的配比配置溶液，用输液装置分别将三种浓度依次增大的溶液输入缸底，溶液静置一段时间后，用溶液采样装置采样并将吸取上来的少量液体放入测量其折射率。得到折射率与高度的线性拟合关系图5(a)，佐证了理论假设(11)的合理性。

表1 线性折射率梯度下的溶液配比

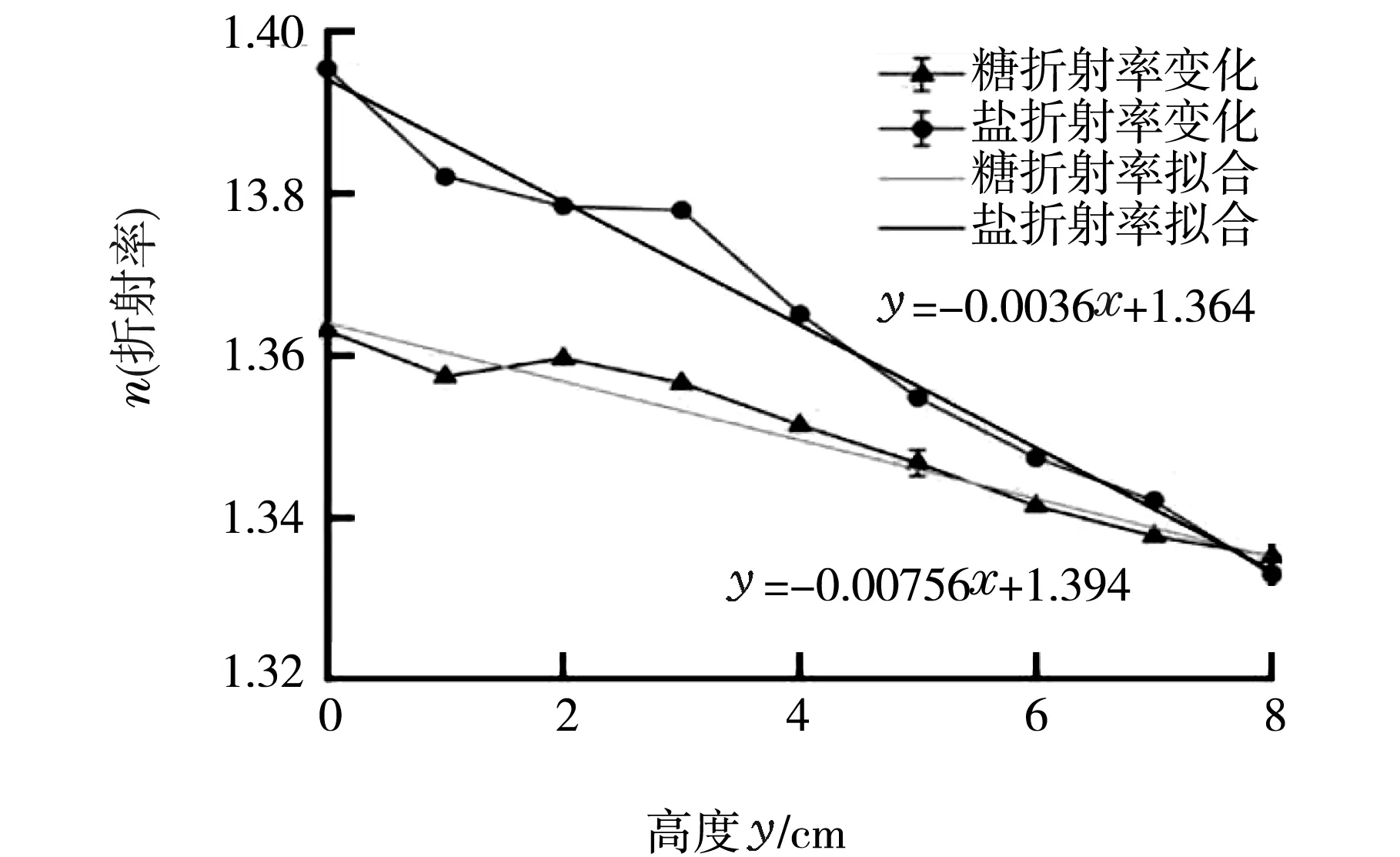
(a)

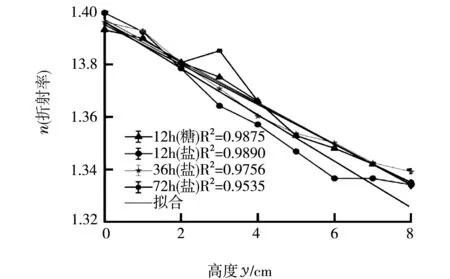
(b)图5 溶液中折射率梯度

由图5(b)，在12h时线性关系最强，此时用入射装置将激光射入盐溶液，改变激光入波长，并在缸前方拍摄激光光路。将照片导入追踪光路轨迹上各点的横纵坐标，得到蓝色、绿色、红色激光的理论光路轨迹与实际轨迹的对比图6。

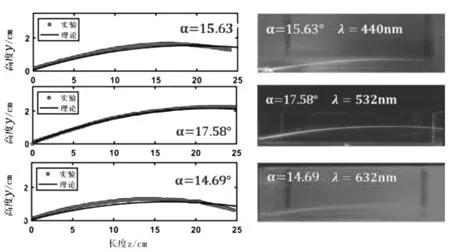
图6 三种波长的理论光路轨迹与实际轨迹的对比图

因为在无机溶质盐溶液中成像更为清晰，故在盐溶液缸的左侧贴上实物“红色三角形”，在缸的右侧拍摄未放置盐溶液的实验原物图7左，并将原物照片代入Matlab计算成像，得到效果图如图7右，“红色三角形”经过溶液折射后，由于折射率线性减小(k>0)，成像并未明显扭曲，而位置向上平移1.1cm，且成像的偏移量与光路轨迹的传输距离的比值约为0.036 6(缸长30cm)，产生了类似于海平面上的“上蜃景”。

图7 实验原图与理论成像对比图

4 总 结

在溶液缸中，使用单束激光来模拟实物反射的光线经过梯度折射率溶液的光路轨迹。在理论上推导了不同时间段，不同波长的激光在非线性及线性折射率梯度溶液中的光路，且考虑了缸壁对光路折射的影响，刻画了激光在溶液中及最终射出缸壁的光路方程。并且基于光路方程，由Matlab计算出了成像，即非线性梯度下成像扭曲，线性梯度下，成像抬升实验上，用三个自制仪器探究了糖，盐酒精溶液下的光路和成像，实验光路和成像与理论光路和成像基本吻合。同时，为教学演示光学现象“海市蜃楼”提供了更定量的理论支撑和可操作性实验装置。