GeH分子电子态的理论研究

徐林轩，刘鑫鹏，罗 旺，李 瑞

(齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006)

GeH分子的光谱性质在半导体薄膜工业中应用非常广泛，所以多年来一直受到人们的广泛关注。研究者使用脉冲KrF(248nm)的准分子激光对GeH4进行光解[1，2]，从而通过化学气相沉积来生长半导体薄膜。现有的实验研究表明，中间基团GeH、GeH2和GeH3可能影响Ge薄膜形成的反应动力学[2]。GeHn的热化学研究可以为理解Ge薄膜生长中的光解过程提供有用的信息[3]。在先前的实验工作中，对GeH的光谱进行了很好的研究，尤其是对于低能电子态。GeH的可见和近紫外能谱是由Kleman和Werhagen首次观察到的[4，5]，确定了a4Σ-的绝热跃迁能(16 747 cm-1)、转动常数(6.765 4 cm-1)和平衡核间距(1.583 4Å)。同时，Barrow等人[6]观察到另一个紫外线谱带系统。Klynning等人[7]通过谱带进行转动分析，推导出了A2Δ态的垂直激发能(25 454 cm-1)。在90年代初，研究人员通过不同的实验方法测量了GeH分子的基态X2Π的红外光谱，并基于实验光谱中得到X2Π态的光谱参数[8-11]。Erman等人[12]对X2Π和A2Δ态进行理论研究，得到势能曲线，并报道了A2Δ-X2Π的跃迁偶极矩和Franck-Condon因子。

本文将对GeH分子的最低三个解离极限对应的8个Λ-S态的光谱性质开展理论研究。给出了解离极限与电子态的对应关系和解离极限之间的能量差，计算了束缚Λ-S态的光谱常数并列出了主要电子组态及其所占比重。最后给出几个束缚态X2Π、a4Σ-、A2Δ和22Σ+的振动能级信息和激发态跃迁到基态的Franck-Condon因子，为后续进一步实验研究提供理论参考。

1 计算方法

在本工作中，关于电子结构的计算研究是应用量子化学计算程序包Molpro2010[13]中开展。具体计算分为三步：首先，用Hartree-Fock自洽场方法(HF)得到GeH分子的基态X2Π的单组态波函数。然后采用完全活性空间自洽场方法(CASSCF)来优化X2Π的波函数获得GeH分子的多组态波函数，其中CASSCF计算选择的活性空间包含的分子轨道为4个a1对称性、1个b1对称性和1个b2对称性，他们对应的是Ge原子的4s4p5s轨道和H原子的1s轨道。最后基于MRCI方法对动力学相关能展开计算。在计算中引入了Davidson修正，来弥补由于对组态空间进行了截断而致使的MRCI能量缺乏大小一致性问题。为了提高计算精度，引入了标量相对论效应和Ge原子3d轨道的电子关联效应。基于MRCI计算获得的单点能，利用LEVEL8.0程序[14]求解一维核运动的Schrödinger方程，得到几个束缚态的光谱常数、振动能级以及Franck-Condon因子。

2 研究结果

2.1 GeH分子的光谱性质

利用MRCI+Q方法计算了GeH分子的能量最低的三个解离极限Ge(3Pg)+H(2Sg)、Ge(3Pg)+H(2Sg)和Ge(1Sg)+H(2Sg)的8个Λ-S态，得到在核间距R从1.1Å到6.0Å范围内一系列的单点能。根据这些能量计算了解离极限之间的能量差值列于表1中，并给出解离极限与Λ-S电子态之间的对应关系。可以看出X2Π、a4Σ-、12Σ-和14Π对应于第一解离极限Ge(3Pg)+H(2Sg)，A2Δ、12Σ+和12Π对应于第二解离极限Ge(3Pg)+H(2Sg)，第三解离极限Ge(1Sg)+H(2Sg)只有一个二重态22Σ+。以第一解离极限作为零点能量，第二、三解离极限与它的能量分离分别为5 898 cm-1和15 268 cm-1，与实验值[15]6 150 cm-1和15 392 cm-1很符合，误差在4%以内。

利用LEVEL8.0程序拟合这一系列单点能求解束缚态的径向Schrödinger方程得到Λ-S态光谱常数(包括平衡核间距Re，绝热激发能Te，解离能De，振动常数ωe和ωeχe，以及平衡转动常数Be)。计算的光谱常数和一些用于参考的实验结果汇总在表2中，还在表3中列出了在核间距平衡位置Re=1.55 Å处主要电子组态及其所占比重。由表2和表3可知，基态X2Π的主要电子组态是8σ29σ24π1(97.2%)，本工作计算的X2Π的ωe、ωeχe、Be、Re和De分别为1 938.275 0 cm-1、32.733 5 cm-1、6.888 3 cm-1、1.570 6Å和2.997 8 eV，与实验结果一致，误差仅为37.893 0 cm-1(2.0%)、0.768 9 cm-1(2.3%)、0.158 3 cm-1(2.4%)、0.016 6Å(1.0%)和0.102 2 eV(3.3%)。第一激发态a4Σ-的是四重态，主要电子组态为8σ29σ14π2(95.2%)对应于基态9σ→4π的单电子跃迁，其垂直激发能Te为15 803 cm-1与实验值吻合。a4Σ-的Be和Re分别为7.183 8 cm-1和1.546 2Å，与实验值的误差分别为0.418 4 cm-1和0.037 2Å。第二激发态A2Δ为二重态，主要电子组态与a4Σ-的主要组态一致也为8σ29σ14π2(97.8%)。对于A2Δ态，Te、Be和Re的值与实验结果基本一致，偏差均小于3%，而ωe和ωeχe的值与实验数据的偏差虽然在可接受范围内，但是相对其他光谱数据来说误差是较大的，这是因为振动常数ωe和ωeχe对势阱的变化很敏感，所以对计算的精度要求较高。激发态22Σ+的垂直激发能为34 706 cm-1，主要电子组态为8σ29σ210σ1(90.8%)，与基态相同。

表1 GeH的解离极限对应关系与能量差

表2 GeH的束缚Λ-S态的光谱常数

表3 Λ-S态在Re=1.55Å处的主要组态及其所占比重

续表

2.2 振动能级和Franck-Condon因子

束缚态X2Π、a4Σ-、A2Δ和22Σ+的振动能级通过LEVEL8.0程序得到，结果整理于表4。a4Σ-、A2Δ和22Σ+的势阱深度分别为1.05eV、0.57eV和0.59eV，能容纳的最大振动能级分别为ν=8、ν=6和ν=6。而基态拥有很深的势阱为3.0eV，因此能容纳更多的振动能级，表4中基态的振动能级仅展示了前20个。

根据Franck-Condon原理[17]，电子态振动波函数的Franck-Condon因子能够定量的描述ν′←ν″谱带的强度分布。Franck-Condon因子由LEVEL程序计算得到，Franck-Condon因子表达式如下：

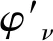
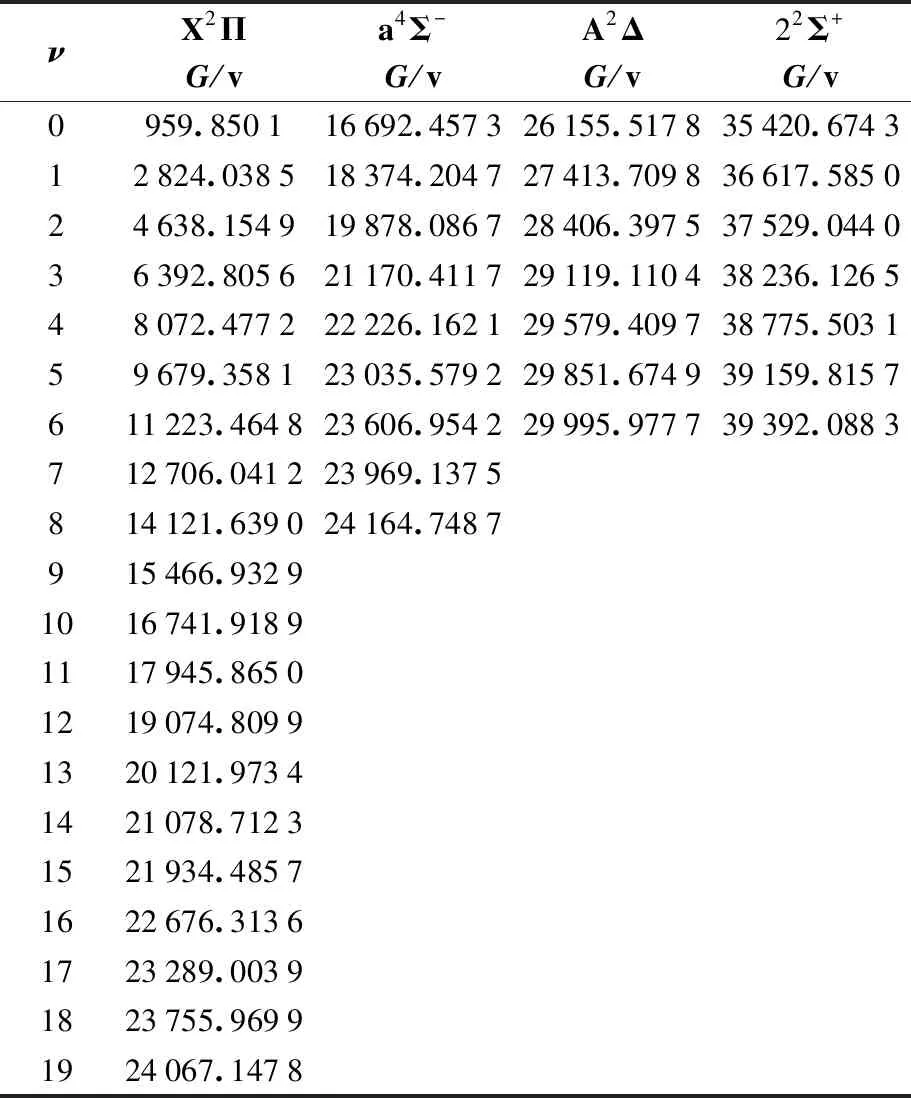
表4 X2Π、a4Σ-、A2Δ和22Σ+态的振动能级/ cm-1

表5 a4Σ--X2Π、A2Δ-X2Π和22Σ+-X2Π的Franck-Condon因子

3 结 语

应用高精度的组态相互作用方法开展了GeH分子的束缚态电子结构的理论研究。明确了最低三个解离极限与电子态的对应关系，解离极限之间的能量差与实验值吻合。确定了束缚态X2Π、a4Σ-、A2Δ和22Σ+的光谱常数并列出了在核间距平衡位置Re=1.55Å处主要电子组态及其所占比重，这些结果都与实验值接近。利用数值方法求解一维核运动的Schrödinger方程，获得几个束缚态的振动能级信息，并计算了a4Σ--X2Π、A2Δ-X2Π和22Σ+-X2Π的Franck-Condon因子，与已有的实验值一致。这些数据可以为理解这GeH分子的动力学行为提供更多有用的理论支持，并为后续实验研究提供理论参考。