水利工程中等效内摩擦角在土体表面倾斜时的计算分析

毕程敏

在水利工程实践中，挡土墙有多种结构型式，常用的结构型式有重力式、悬臂式、扶壁式等。在稳定计算中，墙后土压力计算一般可按朗肯土压力理论和库仑土压力理论进行计算。为了计算黏性土中的土压力，常进行简化计算，近似用等效内摩擦角φd来综合考虑粘聚力c、内摩擦角φ值对土压力的影响。目前常用的等效计算原理有3种：土压力相等原则、抗剪强度相等原则、土压力力矩相等原则。现主要对常用的第1种等效原理进行分析，根据其在土体表面倾斜时的相关计算，结合案例分析和讨论，为具体工程设计提供一定的借鉴。

1.等效原理

当挡土墙墙高h，墙后填土重度为γ，内摩擦角φ，粘聚力c，等效内摩擦角按土压力相等原理，常用的等效计算公式如下：

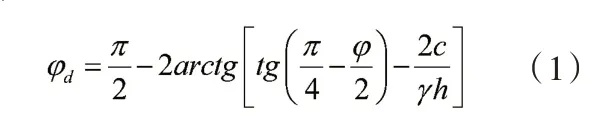
其原理为等效前后墙后主动土压力相等，则原始计算公式为：

式中：

Ea1、Ea2—等效前、后墙后主动土压力(kN)；

γ—墙后填土重度(kN/m3)；

H—挡土墙高度(m)；

c—填土的粘聚力；

φ—填土内摩擦角(°)；

φd—填土等效内摩擦角(°)。

由Ea1=Ea2计算得出式(1)，从以上公式可以看出，在填土面水平情况下，完全可以用公式(1)计算出等效内摩擦角。但是，当填土面倾斜时，则不能用此公式进行计算。原因在于，从上述等效计算公式可以看出，此原理是建立在填土面水平情况下，按郎肯土压力公式进行推导的，此时主动土压力系数为：

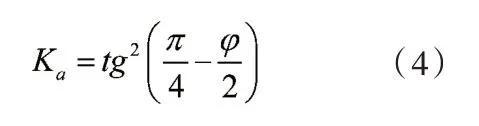
而根据郎肯土压力理论，当填土表面向两侧伸张足够数量时，填土内产生两簇直线破裂面，两簇剪切面所夹的体内填土各点均处于塑性平衡状态，此时主动土压力系数为：

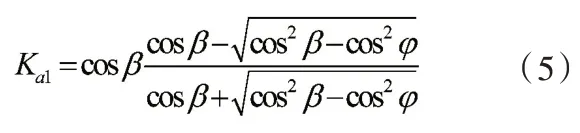
式中：

φ—填土内摩擦角(°)；

β—填土面倾角(°)。

当β=0时，式(5)等于式(4)。按照等效原理，当β≠0时，应按下式计算等效内摩擦角φd：

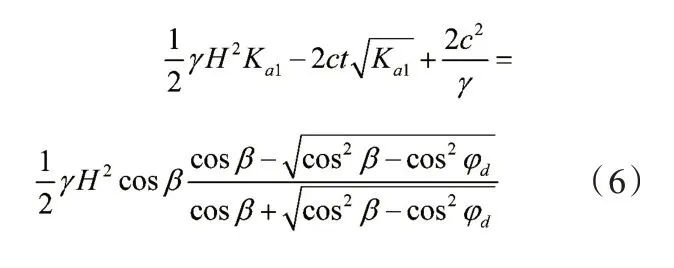
2.具体案例

某悬臂式挡土墙为4级建筑物，钢筋混凝土结构，重度为25kN/m3，作用于中等坚实的土质地基上，地基承载力为120kPa。挡土墙墙高6.0m，基底面与地基土的摩擦系数为0.35，墙后填料为砂壤土，重度为19kN/m3，内摩擦角为20°，粘聚为力12kPa，墙后地面坡度1∶4，挡土墙断面如图1。

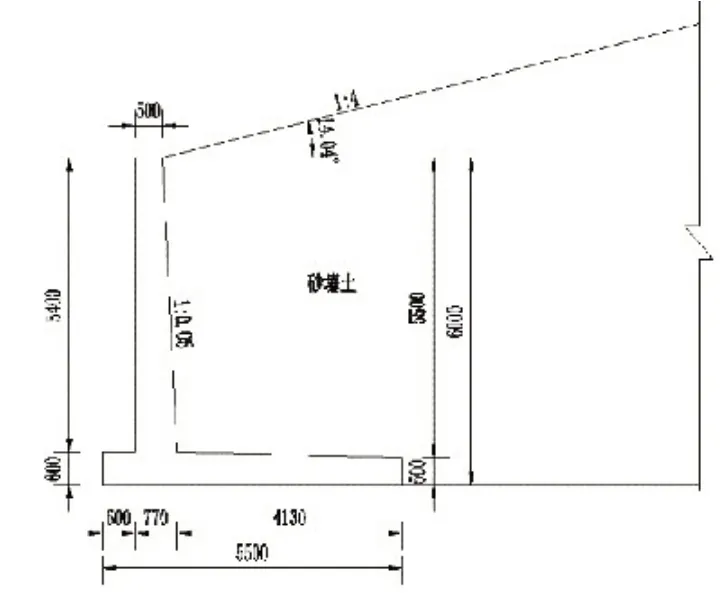
图1 挡土墙横断面图

为简化计算，这次计算仅考虑基本组合情况，无地下水影响，抗滑稳定安全系数不小于1.20，挡土墙平均基底应力不大于地基允许承载力，最大基底应力不大于地基允许承载力的1.2倍，基底应力最大值与最小值之比不大于2.0。计算公式如下：

2.1 抗滑稳定计算公式：

式中:

Kc—挡土墙沿基底面的抗滑稳定安全系数；

f—挡土墙基底面与地基之间的摩擦系数，取0.35；

∑G—作用在挡土墙上全部垂直于基底面的荷载(kN)；

∑H—作用在挡土墙上全部平行于基底面的荷载(kN)。

2.2 挡土墙基底应力计算公式：

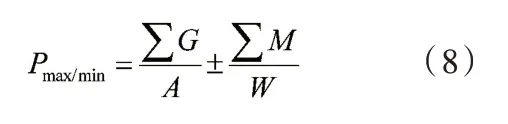
式中：

Pmax/min—挡土墙基底应力的最大值或最小值(kPa)；

∑M—作用在挡土墙上全部荷载对于水平面平行前墙墙面方向形心轴的力矩之和(kN·m)；

W—挡土墙基底面对于基底面平行前墙墙面方向形心轴的截面矩(m3)；

A—挡土墙基底面的面积(m2)；

其余符号同上。

3.计算过程

此时填土面倾斜，等效内摩擦角计算时应按式(6)计算，高度Ht采用墙踵处土体垂直高度，则墙后填土等效内摩擦角为31.49°；若采用式(1)计算，等效内摩擦角为34.84°。

3.1 按黏性土计算

朗肯理论是从半无限土体任意点的极限应力状态出发，提出土压力理论及计算方法。对于悬臂式挡土墙，当墙后填土面倾斜时，其计算方法见图2。主动土压力作用面为墙踵BM，计算公式见式(4)和式(5)，作用方向与填土面平行。朗肯主动土压力计算公式为：

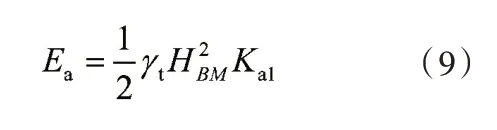
因墙后填土有粘聚力c，主动土压力计算公式中HBM需要减去自稳段高度Z0，其计算公式见式(10)：

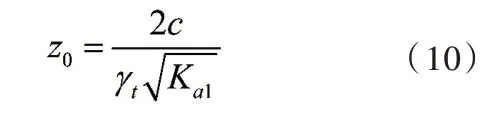
通过计算得知，主动土压力为164.56kN，与水平面夹角为14.04°，根据三角函数关系可将Ea分解为垂直向土压力Ey和水平向土压力Ex，结合挡土墙自重和土体MDEN重量，可求出挡土墙抗滑稳定系数和墙趾墙踵处应力比，计算结果如表1。

3.2 等效后按郎肯理论计算

其计算简图同见图2，此时等效内摩擦角按31.49°计算成果如表2，抗滑稳定系数为1.51，与表1计算结果一致。若按34.84°进行计算，则计算成果如表3，抗滑稳定系数为1.75，则会出现计算结果不同的情况。

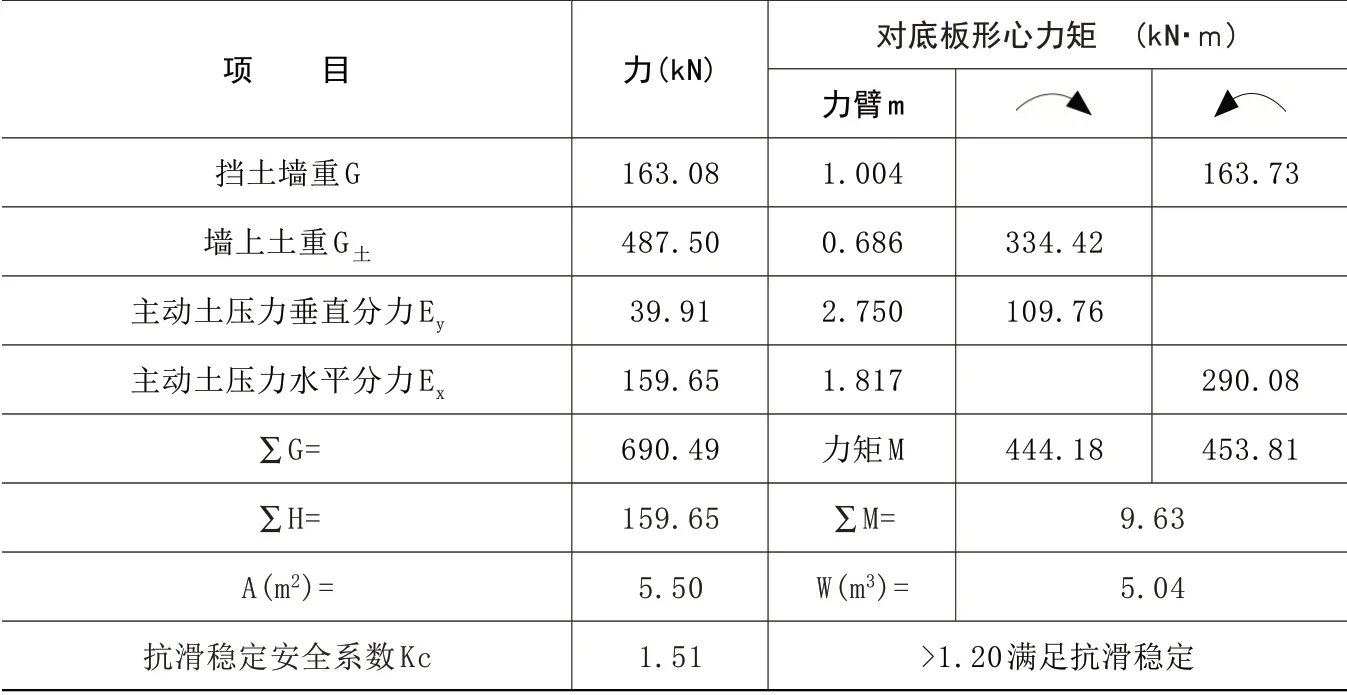
表1 朗肯理论计算成果表（按黏性土考虑）

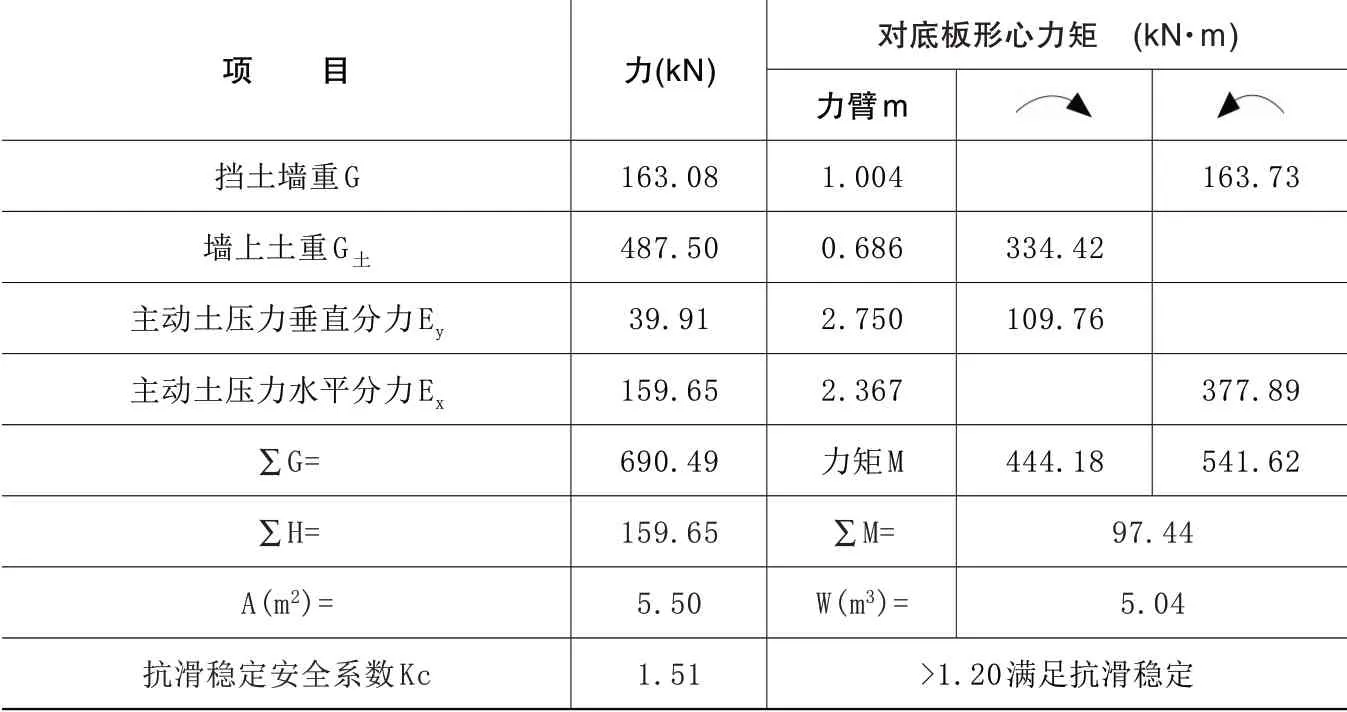
表2 朗肯理论计算成果表（等效内摩擦角31.49°）

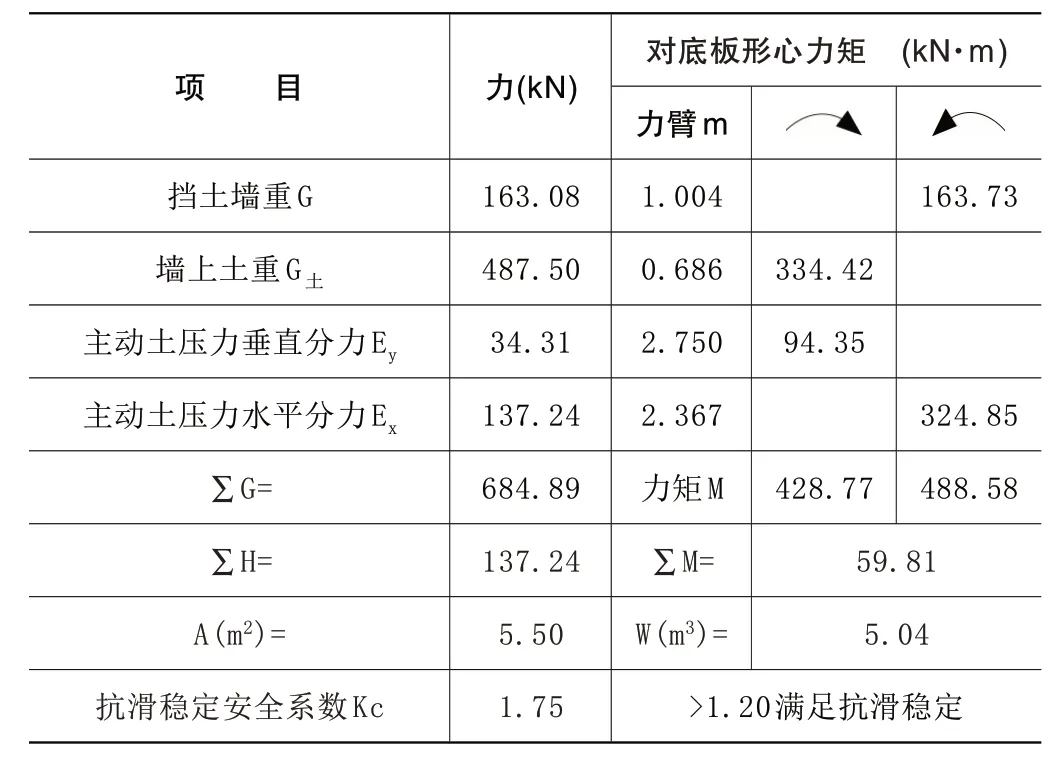
表3 朗肯理论计算成果表(等效内摩擦角34.84°)

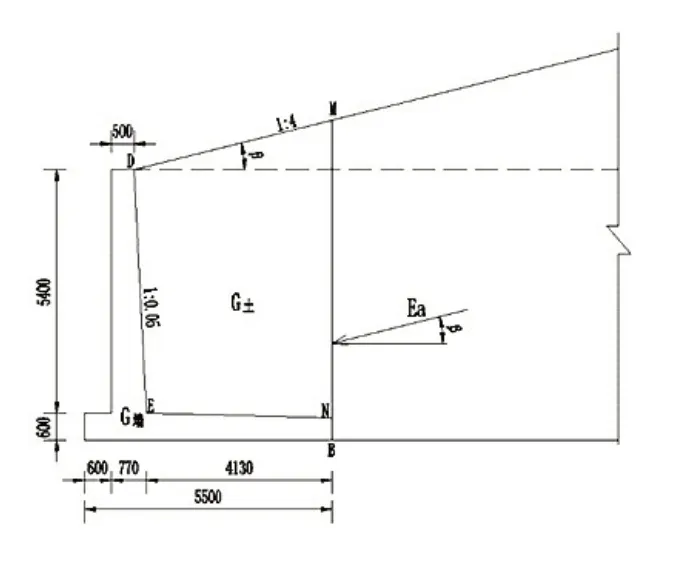
图2 挡土墙朗肯土压力计算示意图

3.3 等效后按库仑理论计算

采用库仑理论计算时，墙后会形成第一破裂面，对于ABC破坏棱体来说，其上作用有3个力，即破坏棱体自重W、主动土压力的反力Ea和破裂面的反力R，棱体处于极限平衡状态，3个力必然闭合。第二破裂面为DB面还是其他面，则由棱体作用三力平衡得出。此算例中存在第二破裂面AB，库仑土压力计算示意见图3。

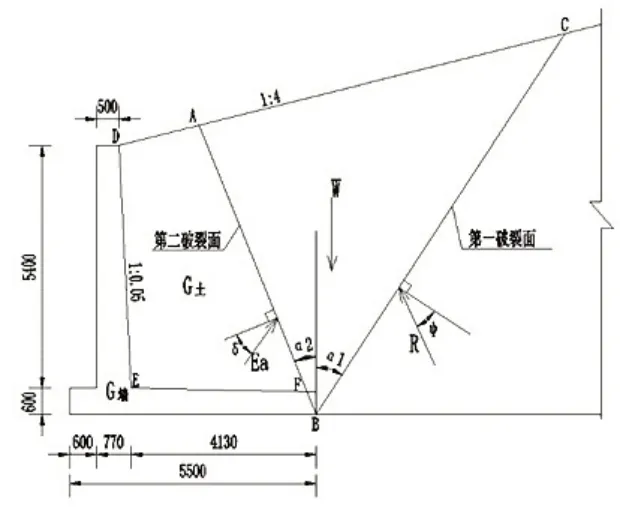
图3 挡土墙库仑土压力计算示意图

当等效内摩擦角为31.49°时，经计算得知：第一破裂角α1为36.06°，第二破裂角α2为22.45°，主动土压力Ea为271.22kN，与AB面垂线夹角为内摩擦角31.49°，与水平面夹角为53.94°。根据三角函数关系，可将Ea分解为垂直向土压力Ey和水平向土压力Ex，结合挡土墙自重和土体ADEF重量，可求出挡土墙抗滑稳定系数和墙趾墙踵处应力比，计算结果见表4。同理，当等效内摩擦角为34.84°时，计算结果如表5。

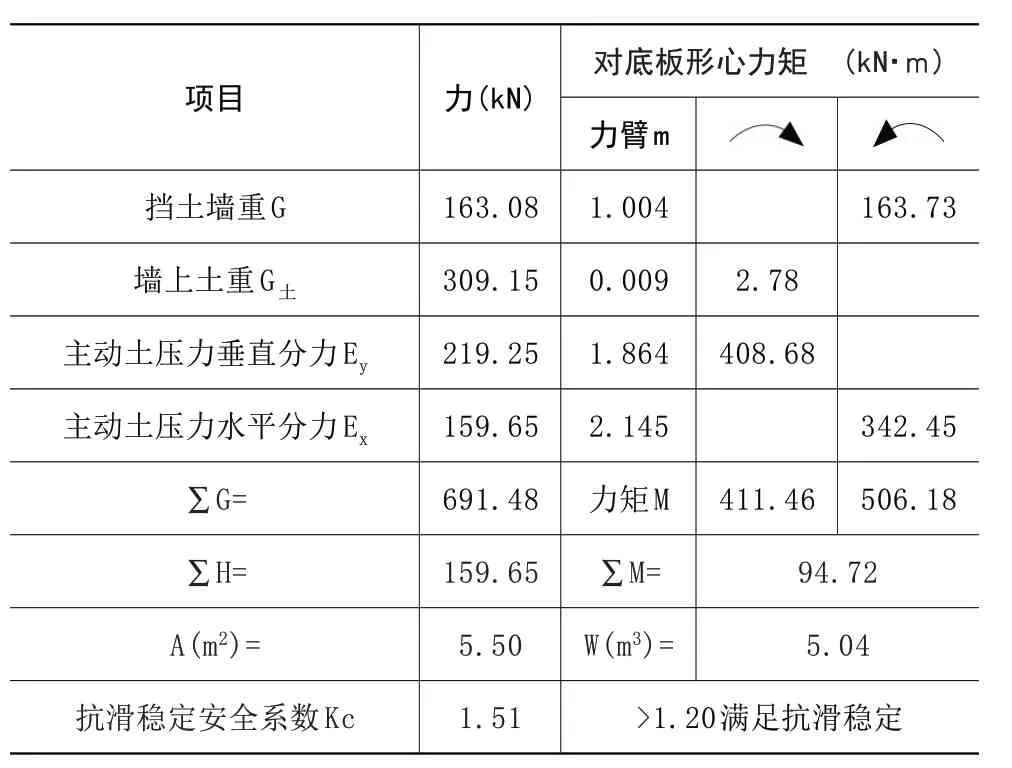
表4 库仑理论计算成果表(等效内摩擦角31.49°)

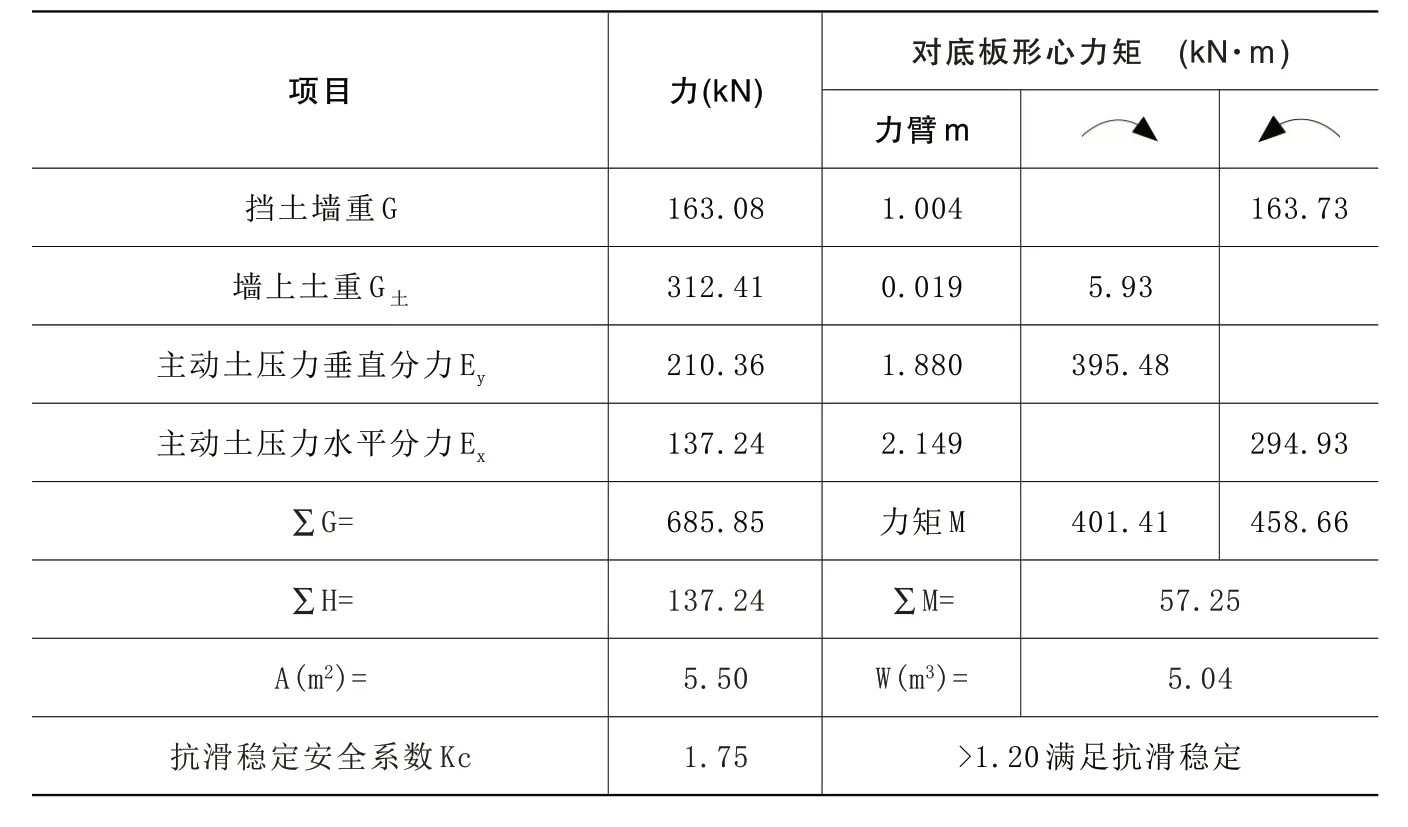
表5 库仑理论计算成果表(等效内摩擦角34.84°)

4.结语

通过表1～表5得知：在进行悬臂式挡土墙抗滑稳定计算时，无论是采用黏性土指标，还是等效内摩擦角指标，计算结果均是相同的。但是，前提是对等效原理计算公式选择正确，尤其是当填土表面倾斜时，若直接采用公式（1），则会出现计算结果不同的情形，因为其适用条件为填土面水平(β=0)。这时应从土压力等效原理出发，采用公式(6)进行计算，则计算结果一致。