基于改进一维逻辑正弦混沌映射系统的图像加密算法

2021-10-21邹东尧李志刚

科学技术与工程 2021年28期

邹东尧，李明，李军，李志刚

(1.郑州轻工业大学计算机与通信工程学院，郑州 450000； 2.中国移动通信集团河南有限公司网络部，郑州 450000)

随着科学技术与互联网的快速发展，数字图像也因保真度比较高，形象生动等特点成了交流间最广泛地沟通介质。然而，互联网的开放性越来越强，图像的安全传输存在着一定的安全隐患。从而，使用图像加密方法，保障图像信息安全是目前的研究热点之一[1-2]。

目前的图像加密方案一般分为两种，一种是产生新的混沌系统以产生更加复杂的混沌序列；另外一种是产生新的加密算法的结构设计。第一种加密方案中，许多学者都会对简单的混沌系统提出改进的方案。混沌是由非线性的确定系统产生的类随机现象，它具有很多特点，如遍历性、有界性、对初始条件的极端敏感性等，在许多领域都有广泛的应用，同时也非常适合应用于图像加密系统[3-8]。低维的混沌映射结构简单，但是概率密度分布不均匀[9]，且混沌范围较小。有学者在简单的混沌系统基础上进行改造，使其成为比较复杂的混沌系统以产生更加复杂的混沌序列。文献[10]中对经典的Logistic 映射增加模运算并对生成的序列进行二进制比特重排，生成具有更好混沌特性的伪随机序列并用于加密系统的置乱和扩散阶段；文献[11]中提出了一种位反转的方法，通过对其分数位的阶数来倒换混沌状态值(表示为不动点数)，修正后的混沌映射刻画了更好的混沌性能，具有更高的复杂度和更大的混沌参数范围；文献[12]中在Logistic映射和Sine映射基础上提出的二维(2D)逻辑正弦耦合图(logistic-sine-coupling map, LSCM)具有更好的遍历性，更复杂的行为和更大的混沌范围。第二种加密方案在混沌序列的产生过程上没有太多的研究，但是在加密算法的结构上有着很多不同的设计方案。文献[13]结合耦合映像格子-S盒(coupled mapping lattice-sbox，CML-SBox)和对称矩阵变换(symmetric transformation matrix，SMT)生成密钥流，通过SMT生成的初始密钥流组成两个一维数组对原图像像素进行置乱，然后用SBox生成最终密钥流与分块后的图像像素进行异或，最后将后一块的密文与前一块的密文进行异或，进行扩散进而达到图像加密的目的；文献[14]提出一种结合Intertwining Logistic映射和动态DNA编码与运算的彩色图像加密算法实现图像的加密。同时也有两种方案一起用来提高加密的安全性；文献[15]使用改进的混沌映射和置换有序二进制编码的密文域可逆信息隐藏，从而达到加密的效果；文献[16]提出了一种新的基于多重混合哈希函数和循环移位函数的混沌图像加密一次性垫方案，采用循环移位函数和分段线性混沌映射(piece wise linear chaotic mappings, PWLCM)，赋予每个移位数混沌的特性，对图像进行扩散，也具有很好的安全性。

1 提出的混沌系统

1.1 经典的混沌映射

Logistic映射是经典的一维映射，被广泛应用于混沌序列的产生中，其表达式为

xn+1=δxn(1-xn)

(1)

式(1)中：xn为输入图像混沌序列值，xn∈(0,1)；xn+1为输出图像混沌序列值；系统调节参数δ的取值范围为[0,4]，其分岔图如图1所示，纵坐标X表示图像混沌序列值，当δ∈[3.57,4]时，逻辑映射系统表现为混沌状态，当δ≈4时，逻辑映射分布呈现最大。

图1 Logistic映射分岔图Fig.1 Logistic map bifurcation diagram

Sine映射同Logistic映射一样，也是经典的一维映射，其表达式为

xn+1=δsin(πxn)/4

(2)

参数δ的取值范围为[0,4]。当δ∈[3.48,4]时，逻辑映射系统表现为混沌状态，其分岔图如图2所示，当δ≈4时，逻辑映射分布呈现最大。

图2 Sine映射分岔图Fig.2 Sine map bifurcation diagram

1.2 改进的混沌系统描述

由于经典的一维逻辑映射Logistic映射和Sine映射存在控制参数范围受限和点分布不均匀等问题，本文结合经典一维逻辑映射Logistic映射和Sine映射提出1-LSCMS混沌系统，其表达式为

xn+1=δ8[1+8δsin(pixn)β]mod1

(3)

式(3)中：xn∈(0,1)；δ、β为系统调节参数，控制系统的混沌性能；mod表示取余操作；β的取值会对混沌状态的范围产生影响，通过实验测试，当β=5时，系统混沌性能较为理想。

1-LSCMS系统的分岔图如图3所示，当δ∈[0.59,15]时，分岔图呈现混沌状态，参数范围较Logistic映射和Sine映射有明显提升。且当δ>0.59时，混沌系统不存在周期窗口。

图3 1-LSCMS系统的分岔图Fig.3 1-LSCMS system bifurcation diagram

1.3 性能分析

1.3.1 敏感性分析

对初值敏感是混沌系统的一个重要属性，这个属性可以通过李雅普诺夫指数(Lyapunov exponents，LE)进行量化。通过LE图像可以直观地看出，某个系统或者映射是否是混沌系统或映射。LE>0时，系统进入混沌状态，存在混沌行为，且混沌性的强弱跟LE指数的大小呈正相关；LE<0时，系统的运动状态会相对来说较稳定，但对初始状态不敏感；LE=0时，系统处于稳定状态。图4(a)为Logistic映射的LE指数图，当δ>3.57时，LE>0；图4(b)为Logistic映射的LE指数图，当δ>3.464时，LE>0；图4(c)为1-LSCMS映射的LE图，当δ>0.59时，LE>0。通过对比可知，1-LSCMS的混沌范围大于Logistic映射和Sine映射。

图4 LE对比 Fig.4 LE comparison

1.3.2 香农熵

香农熵(Shannon entropy，SE)通过度量信号中产生新模式的概率大小来衡量时间序列复杂性。香农熵的值越低，生成的样本序列相似性越高；反之，香农熵的值越大，样本序列就越复杂。因此可以利用香农熵来度量1-LSCMS系统产生混沌序列的复杂度。图5为1-LSCMS系统产生混沌序列复杂度的测试结果。可以看出，当δ≈3.1时，1-LSCMS混沌系统的SE趋于稳定，且SE平均值均大于Logistic和Sine混沌映射。综上，相比较于一维混沌映射Logistic和Sine比起来，1-LSCMS混沌系统产生的混沌序列具有更高的复杂度。

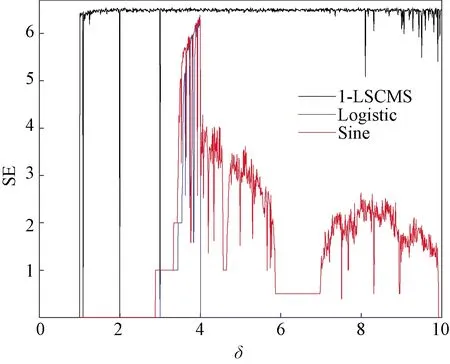
图5 3个混沌系统香农熵对比Fig.5 Comparison of SE of three chaotic systems

2 加密算法设计

2.1 生成初始值及密钥

(4)

(5)

κ1=(S2+S3)/256

(6)

(7)

κ2=(S1+S3)/256

(8)

(9)

κ3=(S2+S4)/256

(10)

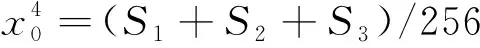
(11)

κ4=(S2+S3+S4)/256

(12)

式中：m=8；n=8；S1、S2、S3、S4为Si的子序列，i=1,2,3,4。

2.2 加密过程

假设需要加密的明文图像的大小为M×N，G(i,j)表示图像像素矩阵中第i行，第j列的像素灰度值。加密算法分为置乱和扩散两个部分。首先，利用1-LSCMS混沌系统产生的混沌序列来对图像像素的位置进行置换。其次，再利用1-LSCMS混沌系统产生的混沌序列所形成的索引矩阵来进行循环移位操作从而改变原本像素矩阵位置上的像素灰度值的大小，在置乱的基础上进行扩散操作从而达到加密的效果。图6为加密过程流程图。

图6 加密过程流程图Fig.6 Encryption process flow diagram

2.2.1 置乱过程

利用1-LSCMS混沌系统产生的混沌序列来对图像像素位置进行置换的流程如下。

Step 2进行一轮置换，按值大小对B进行升序排序，得到序列B′=[b′1,b′2,…,b′M×N]。根据B′相对于B元素位置变化，A也会得到一个相应的置换后的序列A′=[a′1,a′2,…,a′M×N]。

置换图如图7所示，B经过排序后形成B′，A根据与B的一一对应关系进行置换形成置换后的一维矩阵A′，A′即为一轮像素位置置换后的序列。

图7 第一轮像素位置置换图 Fig.7 The first round of pixel position replacement map

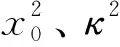
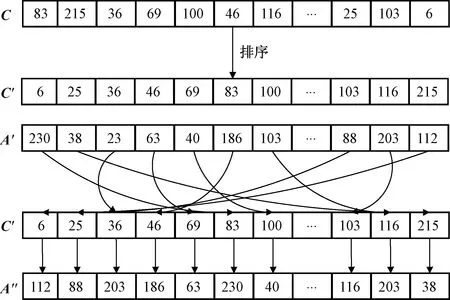
图8 二轮像素位置置换图Fig.8 The second round of pixel position replacement map

E(M×N)=reshape[A″,(M,N)]

(13)

利用1-LSCMS混沌系统产生的混沌序列来对图像像素大小进行置换的过程如下。

在像素位置被置换的基础上进行像素灰度值大小的改变，即在A″基础上改变像素灰度值的大小。采用的1-LSCMS混沌系统产生的混沌序列产生索引矩阵，利用索引矩阵来对改变图像的像素灰度值大小。

图9 像素大小置换过程图 Fig.9 Pixel size replacement process diagram

G′(i,j)=G[ln(A″),j]

(14)

(15)

E″(M×N)=reshape[E′(M×N),(M,N),1]

(16)

式中：G(i,j)为图像像素矩阵中第i行，第j列的像素灰度值；G′(i,j)为索引矩阵中第i行，第j列的像素灰度值；xn为输入图像混沌序列值；xn+1为输出图像混沌序列值；A(i)为图像的第i个像素值。

2.2.2 扩散过程

Q=A′⊕A″⊕E″⊕F

(17)

2.3 解密过程

解密过程是加密过程的反过程，将密钥按照相反的方向迭代即可正确解密。

3 仿真实验及性能分析

3.1 仿真结果

以尺寸为512×512的Baboon，Barbara以及Boats图像为例测试所提出算法的正确性，其加密以及解密图像如图10所示。

图10 仿真结果Fig.10 Simulation results

3.2 密钥空间分析

3.3 直方图分析

直方图是反映数字图像中像素灰度级出现的频率的一种最直观的方法之一，它的分布情况可以直观地体现出像素灰度值。像素分布越均匀，攻击者就越难从直方图中得到有效信息，从而达到加密的效果。好的加密方法可以使加密图像的像素分布均匀。如图11所示。从明文图像直方图中可以看出，像素分布比较集中，密文图像直方图中可以看出，像素分布比较均匀，说明了该算法对图像的信息有很好的隐藏能力。

图11 图像直方图 Fig.11 Image histogram

3.4 卡方测试

直方图可以直观地观测到像素分布是否均匀，χ2可以在数值上更加准确的展现像素的分布，其表达式为

(18)

式(18)中：i为像素值；fi为i出现的次数；f0为i的期望频率。显著水平为α=0.05时，测试结果小于293.247 8时即代表通过测试。

从表1可以看出，Baboon、Barbara和Boats的密文图像卡方测试结果分别是274.705 1、 279.138 7、 272.976 6，结果都小于293.247 8，即卡方测试都在范围内，证明有较好的加密效果。

表1 χ2测试结果

3.5 相邻像素分析

数字图像经过扩散灰度值会发生变化，扩散程度用相关性表示，即相邻像素之间的关系，一个好的加密方法会使密文图像的相邻像素之间关系变小，证明加密效果较好。用相关系数来分析相邻像素之间的关系，其表达式为

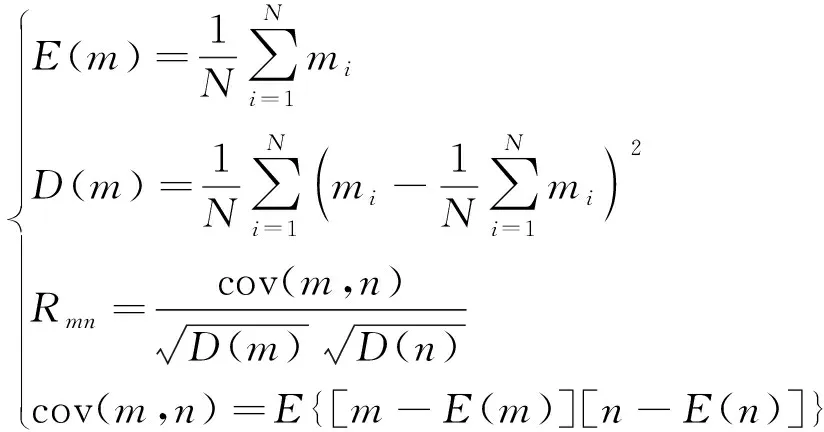
(19)

式(19)中：m和n为两个不同图像的像素值；N为像素的总数目；E(m)为平均值；D(m)为变量m的方差；cov(m,n)为协方差。

图12以Baboon为例，展示明文图像在水平方向、垂直方向以及对角线方向的相关性关系图。图13以Baboon为例展示密文图像在水平方向，垂直方向以及对角线方向的相关性关系图。可以看出，Baboon明文图像的像素在3个方向都是在对角线方向比较集中，相关性相对来说较高，而其密文图像的像素在3个方向都是均匀分布，相关性比较低，证明该算法能很好地对图像进行加密。

用相关系数来更加准确的表达出像素间的关系，相关系数越接近于1证明相关性越高，相关系数越接近于0证明相关性越小。从表2可以看出，3个图像的明文图像的相关系数接近于1，而密文图

像的相关系数很接近于0，证明明文图像的相关性较高，密文图像相关性较低。文献[13]提出了基于二次密钥加密快速的图像加密算法；文献[15]提出了一种位置置乱和交叉换位相结合的加密算法，与这两种加密算法相比，本文算法使密文图像的相关系数更接近于0，能够更好地降低图像相邻像素的相关性。

3.6 信息熵分析

信息熵是被用来作为一个系统的信息含量的量化指标的参数之一，事件发生概率越高，其携带的信息量越低，其值越接近8证明像素值包含的信息量越少，分布越随机，其表达式为

(20)

式(20)中：H(m)为所需要求得信息熵；g(mi)为灰度值i出现的频率；M-1为灰度等级。

表3为Baboon，Barbara和Boats三幅图像以及文献[13]和文献[18]的明文图像与密文图像的信息熵的值，可以看出，密文图像的信息熵都特别接近于理想值8，但与文献[13]和文献[18]相比，使用本文算法得到的密文图像的信息熵更接近于理想值，所以证明了本文算法能很好地满足加密安全性需求。

表3 图像信息熵

3.7 差分攻击

差分攻击属于图像加密攻击方式中的选择明文攻击，攻击者可以选择改变图像中的某个像素后对其进行加密，与原来加密后的图像进行对比，找到两者之间的差异从而得到明文密文之间的关系从而攻击加密算法。目前像素改变率(number of pixels change rate，NPCR)和统一平均变化强度(unified average intensity，UACI)[19]是评价差分攻击的两个常用指标，其表达式分别为

(21)

(22)

式中：g1(i,j)为明文图像i行j列像素值；g2(i,j)为密文图像i行j列像素值；D(i,j)表示g1(i,j)和g2(i,j)所对应的像素值是否相同，若g1(i,j)=g2(i,j)，则有D(i,j)=0，否则D(i,j)=1。

NPCR的理论值为99.609 4%，UACI的理论值为33.463 5%，若图像的NPCR和UACI越接近于理论值就证明算法抵御差分攻击效果比较好。改变某个像素值后的明文图像与密文图像的NPCR和UACI如表4所示，其中c1(300,100)表示改变像素位置为(300,100)处的像素值，c1(512,512)表示改变像素位置为(512,512)处的像素值。