基于初始孔隙率的千枚岩损伤模型分析

2021-10-21王允偲邓祥辉赵志清

科学技术与工程 2021年28期

王允偲，邓祥辉，王睿，赵志清

(西安工业大学建筑工程学院，西安 710021)

当隧道在千枚岩地层中修建时，由于千枚岩节理裂隙发育，强度低，容易导致隧道变形过大、衬砌开裂甚至局部坍塌等工程问题[1-2]。因此，需对千枚岩的工程性质进行研究。千枚岩由于成岩历史和赋存环境等因素的影响，导致初始孔隙率差异很大，因而造成不同环境下千枚岩的工程性质相差很大[3]。若不能准确地掌握千枚岩的工程性质，将造成重大工程事故，因此，需对不同初始孔隙率下千枚岩的工程性质进行研究[4]。

为了防止或减少在软岩中施工发生的工程事故，中外学者就此对软岩的性质开展了一系列研究。齐万鹏等[5]对IV、V级千枚岩进行了细致分级，建立了千枚岩围岩施工阶段的亚级分级方法。王睿等[6]利用声波-回弹联合测试法，建立了施工现场围岩快速分级的方法，所建立的围岩快速分级方法与传统的分级方法相比，更加准确快速。周翠英等[7]通过扫描电镜、X射线衍射及物理力学试验等方式测定了泥岩、炭质泥岩等软岩的微观结构、矿物成分、物理力学性质及其随时间的变化特点，揭示了软岩软化的变化规律。杜宇翔等[8]通过X射线衍射、电镜扫描和三轴压缩试验等方式，分析了昔格达组半成岩的微观结构与强度特性，提出了一种新的岩土体的工程分级方式。车平等[9]从物理力学性质、矿物与化学成分、微观结构等方面对巢湖地区坟头组泥岩进行试验研究，发现水沿微裂隙进入岩石内部，溶解可溶盐胶结，使裂隙向纵深发展是导致岩石软化的根本原因。蒋毅等[10]结合岩石的单轴压缩与三轴压缩试验，探究了软硬岩交互地层的力学性质。研究发现复合底层的变形主要发生在软岩部分，因此提出软岩的性质对于工程施工具有重要意义。Yang等[11]对泥质板岩进行了水理性试验和单轴压缩试验，发现随着饱水时间的延长，泥质板岩的峰值强度逐渐下降，泊松比逐渐增大，其破坏形式主要是沿着层理面发生张拉破坏和局部剪切破坏。

在研究软岩的力学性质的过程中，很多学者认为建立力学模型进行分析是比较有效的方法，并对一些软岩如泥岩、板岩等进行了损伤模型分析。如张明等[12]和张慧梅等[13]利用三轴压缩试验并结合岩石损伤理论进行研究，得出了应用于广义岩石的损伤本构模型。田忠喜等[14]根据微元统计理论建立了损伤变量，并引入修正系数调整岩体结构面对围岩的影响，推导出了考虑结构面对岩体影响的损伤本构方程。袁小清等[15]修正了非贯通裂隙岩体的本构模型。温韬等[16]建立能够体现岩石的初始损伤以及损伤部分仍能承受一定应力的新型岩石损伤模型，并建立了相关修正影响因子来修正损伤本构模型。宿辉等[17]基于片麻花岗岩的室内物理试验，探究了不同温度下片麻岩的热损伤规律，建立了考虑温度变化的损伤模型。王伟等[18]和陈俊桦等[19]分别修正了考虑孔隙水压力及考虑岩石完整性系数的岩石损伤本构模型。邵志鑫等[20]利用电子计算机断层扫描(computed tomography，CT)扫描技术，总结了不同冻融循环下矽卡岩的冻融损伤特征，建立了冻融损伤下围岩的损伤规律。对于岩石损伤本构模型的修正，虽然中外学者已经进行了大量的研究[21-22]，但对于岩石的初始孔隙率并未考虑。初始孔隙率是岩石形成过程中产生的原生孔隙，对于初始孔隙率较大的软岩，在力学性质分析中必须考虑初始孔隙率的影响。

在考虑了千枚岩初始孔隙率的条件下，结合岩石损伤力学，在岩石破坏变形的基础上，利用岩石损伤随机分布原理，建立了考虑千枚岩初始孔隙率损伤的本构模型。

1 考虑初始孔隙率的千枚岩损伤模型

1.1 基本假设

当千枚岩受到压力作用时，其应力应变曲线与大部分岩石相同，可以分为四个阶段：压密阶段，弹性阶段，弹塑性阶段，软化阶段。千枚岩在成岩历史过程中，受赋存环境的影响，如地下水、风化、地应力、构造运动等因素的影响，会产生较多影响岩石性质的原生孔隙，将岩石成岩过程中产生的这些原生孔隙定义为初始孔隙。初始孔隙体积与岩石总体积之比即为初始孔隙率。在建立千枚岩损伤本构模型时，既要充分考虑千枚岩四个阶段的变形特性，又要考虑千枚岩内部初始孔隙率对于岩石强度的影响。因此做出如下假设。

假设千枚岩在受到轴向力时可简化为：天然孔隙部分的面积A0、未损伤部分的面积A1和损伤部分的面积A2，如图1所示。

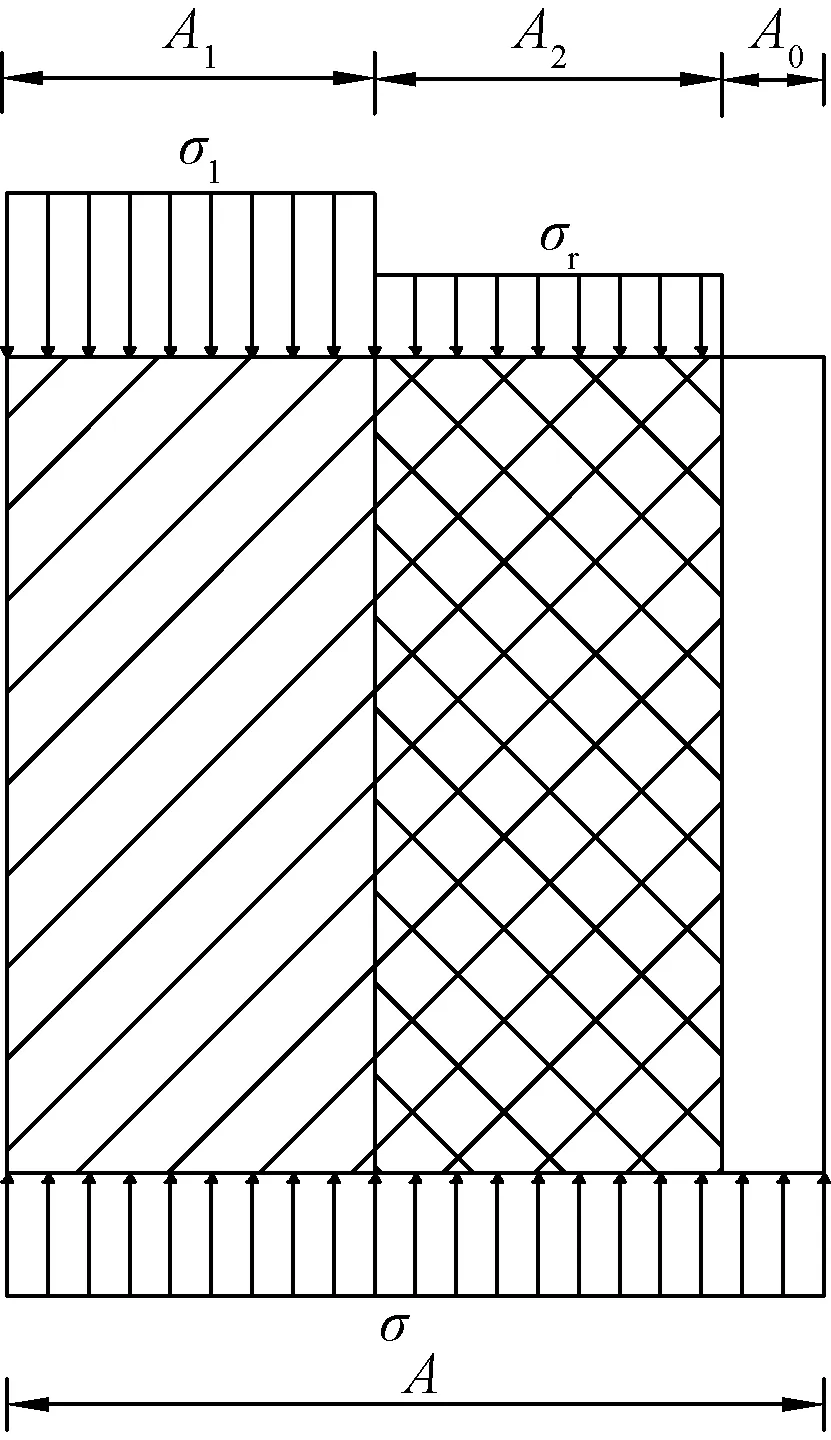
图1 损伤模型受力示意图Fig.1 Schematic diagram of the damage model

孔隙部分无法承受任何荷载，损伤部分承受损伤应力σr，未损伤部分承受有效应力σ1，σ为岩石承受的全部荷载，则其关系式为

σA=σ1A1+σrA2

(1)

式(1)中：A为岩石的面积；A1为未损伤部分的面积；A2为损伤部分的面积。

假设千枚岩受压后，内部损伤仅发生在主应力方向，其他方向不发生损伤，即千枚岩所受荷载仅由未损伤部分与损伤部分共同承担，因此定义损伤变量D为

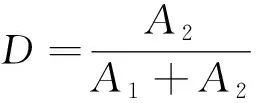
(2)

假设千枚岩作为一个整体，当受到轴向压力作用时，轴向应变相同，同时，内部微元满足如下条件。

(1)微元在弹性变形阶段满足广义胡克定律:假设内部未损伤的微元在弹性变形阶段满足广义胡克定律，根据广义胡克定律，引入有效应力E可得

Eε1=(1+μ)σ1-μ(σ1+σ2+σ3)

(3)

式(3)中：E为千枚岩的弹性模量；μ为千枚岩的泊松比；σ1为千枚岩所受的最大主应力；σ2为千枚岩的中间主应力；σ3为千枚岩所受的最小主应力；ε1为千枚岩的最大主应变。

在单轴压缩条件下，围压为零，即σ2=σ3=0，因此前后方向上的径向应变ε2与左右方向上的径向应变相同，即ε2=ε3，可得

σ1=Eε1

(4)

(2)微元的屈服条件满足Drucker-Prager(D-P)屈服准则。根据Drucker-Prager屈服准则，有

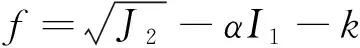
(5)

式(5)中：f为D-P强度准则的表达式；I1为有效应力张量的第一主不变量；α为岩石与内摩擦角φ有关的材料参数；k为岩石与黏聚力c和内摩擦角φ有关的材料参数；J2为有效应力偏张量的第二主不变量，其计算公式分别为

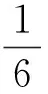
(σ1-σ2)2]

(6)

I1=σ1+σ2+σ3

(7)

(8)

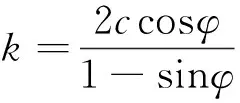
(9)

将式(6)～式(9)代入式(4)，便可得D-P强度准则在三轴压缩条件下的表达式，对于单轴压缩试验，σ2=σ3=0，其计算公式为

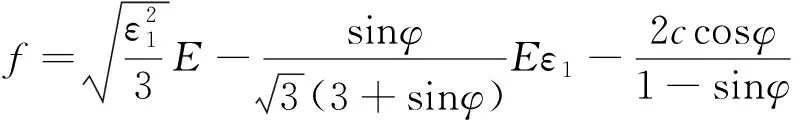
(10)

(3)微元的强度满足Weibull分布。千枚岩内部微元的损伤概率与屈服强度有关，岩体内部的随机微元为损伤微元的概率为p。在达到峰值应变时，内部的损伤微元的数量等于岩石的损伤变量。可知千枚岩内部的损伤变量与微元强度之间的关系为

(11)

式(11)中：p为岩体内部的随机微元为损伤微元的概率；p(f)为达到D-P强度准则的岩石内部微元为损伤微元的概率。

Weibull随机分布是可靠性分析的理论基础，可用来表示内部微元的强度可靠性，并计算微元为损伤微元的概率，因此千枚岩内部损伤的密度函数可表示为

(12)

式(12)中：m和f0为统计参数，是定值，可通过边界条件利用半逆解法求得。

由此，将式(11)代入式(10)并进行积分，可以求出损伤变量为

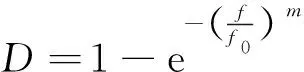
(13)

1.2 千枚岩损伤本构模型的建立

假设千枚岩的初始孔隙率为w，则有

A0=Aw

(14)

结合式(1)、式(2)和式(14)，可以得出考虑损伤变量的应力表达式为

σ[σ1(1-D)+σrD](1-w)

(15)

将式(13)代入式(15)，可将损伤变量替换，得到与屈服强度有关的应力表达式为

(16)

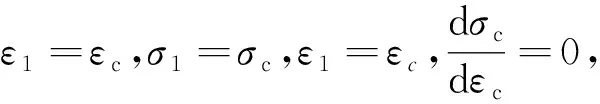
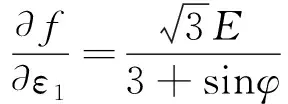
(17)

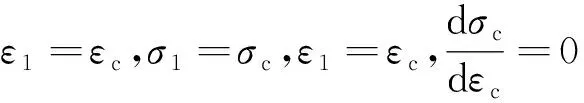
(18)

(19)

将式(18)、式(19)代入式(16)，得到考虑初始孔隙率的千枚岩损伤模型为

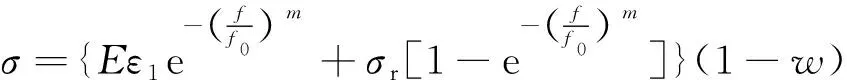
(20)

2 室内试验

2.1 试样制备

四川镇江关—松潘的某铁路隧道穿越的富水千枚岩地带，分别从该隧道的DK232+620、DK520+535、DK807+120、D1K106+370、D1K450+805区段随机选取千枚岩岩样若干，进行室内试验。根据《工程岩体试验方法标准》(GB/T 50266—2013)的规定，将岩样制作成直径为50 mm，高为100 mm圆柱体试块。将采集到的各个区段的岩样按照上述要求制成试块，试块实拍图如图2所示。

图2 圆柱体试件Fig.2 Cylindrical specimen

2.2 孔隙率测试

2.2.1 孔隙率测试原理

千枚岩的孔隙率是采用MesoMR23-060H-I型中尺寸核磁共振成像分析仪测得。在进行核磁共振之前，需对千枚岩运用真空饱水仪进行真空抽气法强制性饱水。

核磁共振是质子在磁场作用下进行弛豫，质子在磁场作用下运动的时间称为弛豫时间，弛豫时间用T2表示，是核磁共振测试的重要参数。由弛豫时间T2可知，核磁共振总的横向弛豫速率为1/T2，1/T2的变现形式为

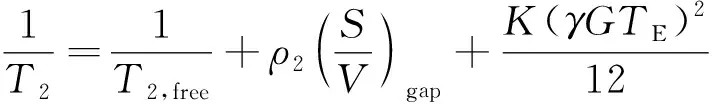
(21)

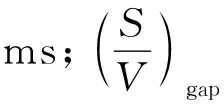
根据式(21)，结合核磁共振的原理可知：千枚岩在强制饱水后，其孔隙内有且仅有一种液体，因此，质子自由弛豫时间T2自由会较长，1/T2自由会较小，可以忽略不计；千枚岩在进行核磁共振试验时，仪器参数合理的调试使得千枚岩处于均匀磁场中，磁场梯度G较小，可以忽略不计，因此核磁共振总的横向弛豫速率的计算式(21)可以简化为

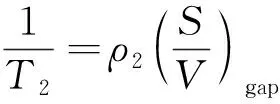
(22)

对于千枚岩核磁共振的试验结果，可根据式(22)推算出孔隙率。

2.2.2 孔隙率分析

核磁共振试验测得同一区段的千枚岩孔隙率相似，为了便于进行后续研究，选取不同孔隙率的千枚岩岩样各一组，孔隙率如表1所示。

表1 岩样孔隙率

根据式(22)以及核磁共振试验所测得的不同区段千枚岩的T2谱，得出了不同区段千枚岩的孔隙半径分布情况，绘制出千枚岩孔隙半径与孔隙率分量曲线，由于孔隙率相似，其孔隙半径与孔隙率分量曲线图基本一致，为方便观察，从每一区段中取一条曲线进行展示分析，如图3所示。

图3 试件孔隙率分布Fig.3 The porosity distribution of the test piece

对图3分析可知：千枚岩内部的孔隙半径为 0～100 μm，其中绝大部分孔隙半径分布在0.01～40 μm。千枚岩孔隙率分布共有2个波峰，分别集中在孔隙半径为0.01、10 μm左右，表明这两种半径的孔隙相比于其他半径的孔隙在千枚岩内部分布较多。结合表1、图3分析可知：当千枚岩内部的孔隙率小于0.5%时，其内部半径为0.01 μm的孔隙数量多于孔隙半径为10 μm的孔隙；当千枚岩内部的孔隙率大于0.5%且小于1%时，其内部半径为0.01 μm的孔隙数量多于孔隙半径为10 μm的孔隙；当千枚岩内部孔隙率大于1%时，其内部各种半径的孔隙数量均明显增多，且高于其他孔隙率的千枚岩。

2.3 应力应变测试

2.3.1 应力应变分析

根据单轴压缩试验所测得的横向峰值应变、纵向峰值应变以及单轴抗压强度，可求得千枚岩的弹性模量与比泊松比。结合表2可以看出，千枚岩孔隙率较小时，其单轴抗压强度的峰值应力较大，峰值应变较小，随着孔隙率的增大，峰值应力在逐渐的减小，峰值应变在逐渐地增大。当千枚岩的孔隙率小于1%时，千枚岩的峰值应力与峰值应变变化不大，当孔隙率大于1%时，千枚岩的峰值应力急剧的下降，峰值应变急剧的上升。

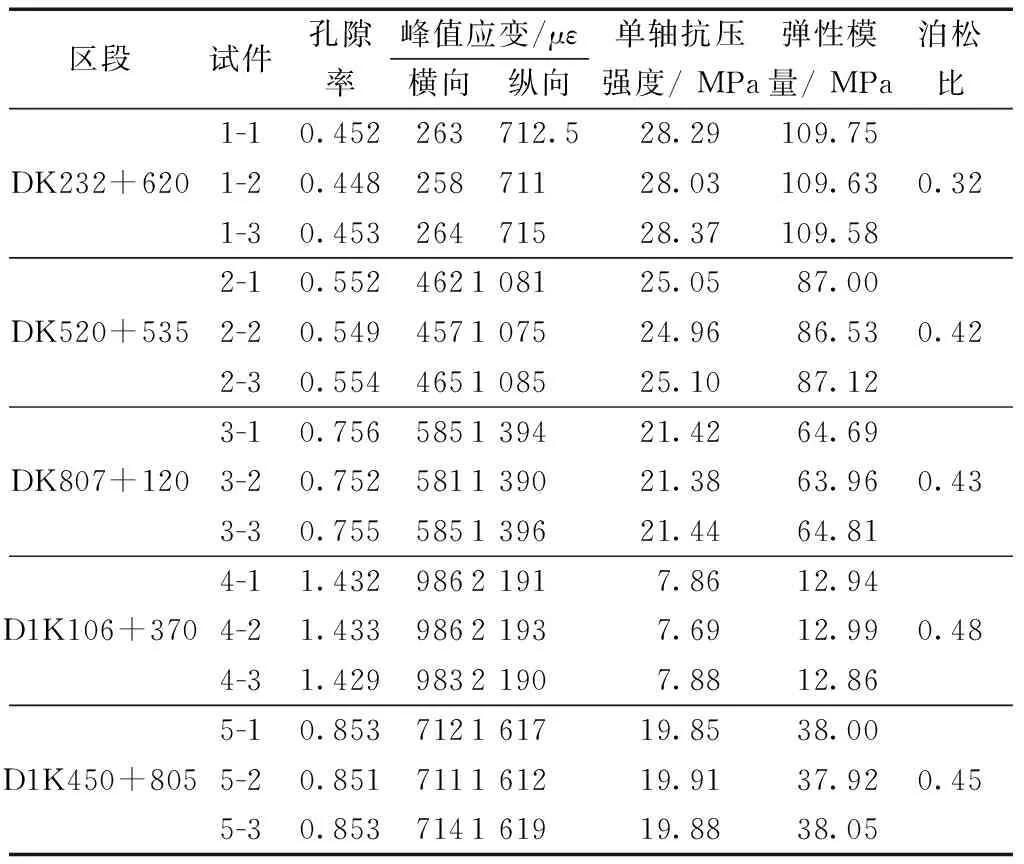
表2 试件的峰值应变和单轴极限抗压强度

将千枚岩的弹性模量与其相应的孔隙率进行拟合，拟合曲线如图4所示。由图4可见，千枚岩弹性模量与其孔隙率的拟合基本吻合，拟合的相关系数R2=0.981 3，拟合关系式为二次多项式，可表示为

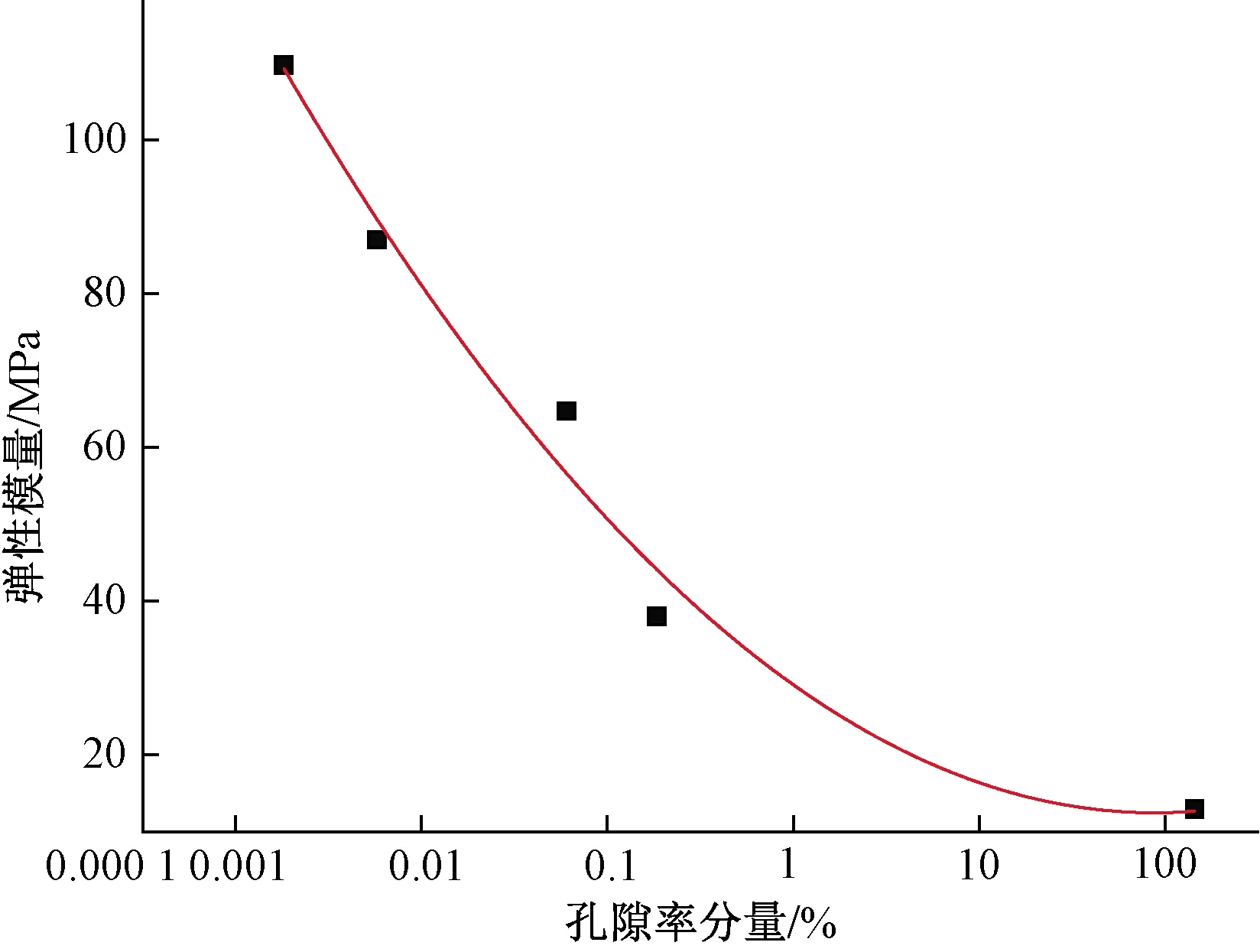
图4 试件弹性模量与其孔隙率拟合曲线Fig.4 Fitting curve of elastic modulus of rock sample and its porosity

E=110.3w2-306.53w+225.28

(23)

由式(23)可知，千枚岩的弹性模量与孔隙率有关，且孔隙率越大弹性模量越小。

2.3.2 应力-应变曲线

对不同区段的千枚岩分别进行单轴压缩试验，得到的数据经过处理，绘制成应力-应变曲线，由于同一区段的孔隙率相近，其应力应变曲线相近，故每一区段取出一条曲线进行展示分析，如图5所示。

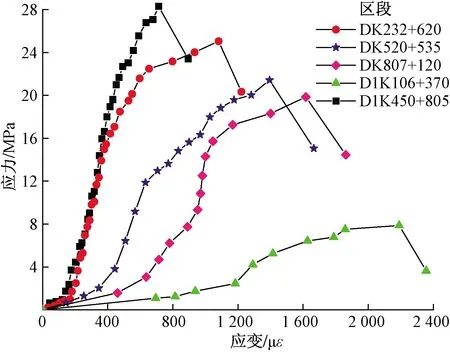
图5 不同区段试件的应力-应变曲线Fig.5 Stress-strain curves of specimens in different sections

从图5可见，5个断面的试件应力-应变曲线表现出类似的规律性，即千枚岩单轴压缩应力-应变全过程曲线的变化规律大致上均可划分为4个阶段。具体分析如下。

(1)第Ⅰ阶段：压密阶段，此阶段应力较小但应变较大，主要原因为千枚岩在竖向荷载的作用下，内部的孔隙逐渐闭合。压密阶段虽有应变，但千枚岩内部微元未发生任何变形。

(2)第Ⅱ阶段：弹性阶段，此阶段应力与应变呈线性相关，主要原因为千枚岩在竖向荷载的作用下，内部微元发生弹性变形。弹性阶段的应力应变关系满足胡克定律，可通过拟合获得弹性模量。

(3)第Ⅲ阶段：弹塑性阶段，此阶段应力与应变不再满足线性关系，应力的加载速度减小，应变的变化速度增大。主要原因是应力达到了塑性阈值，千枚岩开始发生弹塑性变形。

(4)第Ⅳ阶段：软化阶段，此阶段的应力不再增加，应变急剧的增加。千枚岩达到峰值应力后，其承载力逐渐地下降至残余应力。

分析图5可知，不同区段的千枚岩经过单轴压缩破坏后，随孔隙率增大，其第Ⅰ阶段曲线所占比例越大，主要原因是千枚岩内部的孔隙数量与孔隙体积不断累积与增大导致的；第Ⅱ阶段曲线所占的比例逐渐减小，而第Ⅲ阶段曲线将变得平缓，这表明千枚岩随着孔隙率的增大，其弹性阶段逐渐的减小，弹塑性阶段逐渐增大；第Ⅳ阶段的曲线几乎平行，说明千枚岩的软化阶段与孔隙率无关，但残余强度及峰值应力强度与孔隙率相关，且孔隙率越大，残余强度与峰值应力强度越低。

3 本构模型验证

将表2所求得的各参数代入式(20)中，可拟合出不同孔隙率下的应力应变曲线。每组各取一组数据，与相同孔隙率的单轴压缩曲线进行比对，结果如图6所示。可以看出，考虑初始孔隙率的千枚岩损伤本构模型的预测数据与实际数据基本相符，曲线基本重合，但其极限单轴抗压强度均比实际数据略小。

图6 应力-应变预测曲线Fig.6 Stress-strainforecast curve

由表3可知，从15个试样的单轴抗压强度结果看，预测强度值与实测强度值误差范围为0.25%～1.84%，5组试件平均误差分别为1.80%、1.19%、1.77%、0.29%和0.67%。从结果可知，预测值与实测值误差较小，说明预测方法和建立的千枚岩损伤模型是符合实际的。因此该模型可用来预测不同孔隙率下千枚岩的单轴抗压强度与极限应变量，并且孔隙率越大，预测结果越接近。