基于广义Hoek-Brown强度准则的岩质边坡稳定性分析

闫洪超，鲁 杰，饶振兴，翟洪涛，刘 浩，李立辰

(1.河南省地质矿产勘查开发局 第四地质勘查院，河南 郑州 450000；2.中国地质大学(武汉)工程学院，湖北 武汉 430074)

0 引言

岩体强度参数的合理选取是岩体工程工作的主要内容，它直接影响着工程的经济成本和整体安全性[1-2]。随着数值模拟手段的发展，有限元强度折减法因其形式简洁，能较好地考虑岩土体的应力-应变关系，在边坡稳定性分析中得到了广泛应用[3]。目前，采用强度折减法对岩体稳定性分析时，主要基于线性的Mohr-Coulomb强度准则和Drucker-Prager强度准则，然而实际工程岩体的破坏强度包线并非线性，因此，采用非线性的强度包络线更为合适[4]。Hoek-Brown强度准则是由Hoek和Brown基于大量室内岩石三轴试验与现场矿山边坡勘察资料提出的用于估算完整到破碎岩体强度参数的半经验准则[5-6]。经过多次的修正，Hoek-Brown强度准则已广泛应用于岩体边坡稳定性分析中。目前，基于Hoek-Brown准则强度折减法的研究主要包括[7-9]：非线性强度准则的线性转换、强度包线折减，强度参数折减和参数瞬时线性化取值。上述方法的提出对Hoek-Brown准则的理论优化与在数值模拟方法中的应用起到了极大的推动作用，然而，基于实际岩质边坡工程的应用还较少。

本文以某石灰石矿山露采高边坡为例，基于室内岩体三轴试验与现场踏勘资料，引入广义Hoek-Brown强度准则对边坡岩体强度参数进行选取，同时将其转化成等效的Mohr-Coulomb强度参数，结合强度折减法，对边坡稳定性进行数值模拟分析。结合参数敏感性分析方法，对经验参数的取值提出了几点建议。本文研究成果可以为Hoek-Brown强度准则在类似矿山边坡工程稳定性分析中的应用提供一些参考。

1 Hoek-Brown强度准则介绍

1.1 广义Hoek-Brown强度准则

E.Hoek针对狭义Hoek-Brown强度准则的不足之处，对其进行了修正，得出了广义Hoek-Brown强度准则，其理论方程见公式(1)[5-6]：

(1)

式中，m、s、a均为反映岩体特性的半经验参数；其经验取值可通过地质强度指标(GSI)和岩体扰动系数(D)进行估算。

相比于狭义的Hoek-Brown强度准则，广义的Hoek-Brown强度准则的适用范围由完整、强度较高的岩体扩展到了松散和破碎岩体，相比于Mohr-Coulomb强度准则和Drucker-Prager强度准则，能更好地反映岩体的非线性破坏特征。

1.2 广义Hoek-Brown强度准则参数选取

1.2.1 GSI的选取

GSI指标的取值主要基于大量的现场岩石露头和钻孔岩心观察获得岩体的岩性、结构面特征及不连续面等条件，其取值范围为0～100。一旦确定了现场的岩体地质强度指标，便可以根据Hoek提供的GSI取值参考表进行取值估算(表1)。目前，关于GSI指标的取值方法主要包括两类，即插值法和间接法，这也为现场勘察人员提供了极大便捷[10]。

表1 量化的GSI围岩分级表[5-6]

1.2.2D的选取

开挖爆破产生的震动会对一定深度范围内的岩体及结构面产生影响，一方面会产生一定的扰动区，造成扰动区内岩体损伤，岩体强度参数弱化；一方面对边坡形态产生影响，改变边坡原有的约束条件[11-12]。2002年，Hoek等[6]对经验强度准则进行了修正，引入了岩体扰动系数D，对爆破震动和应力松弛对岩体的影响进行了综合考虑，D的取值在0(非扰动岩体)到1(扰动极强岩体)范围内变化(表2)。

表2 岩体扰动系数建议取值

1.3 等效Mohr-Coulomb强度参数获取

在进行数值模拟以及极限平衡分析时，Hoek-Brown准则存在很多的不适用性和不准确性，这是由于目前大多数数值分析软件都是基于线性的Mohr-Coulomb准则开发的，使得非线性的Hoek-Brown准则难以直接应用[12-13]。

研究发现，当σt<σ3<σ3max，Mohr-Coulomb准则曲线与Hoek-Brown准则曲线十分吻合，因此，可采用线性回归法对广义Hoek-Brown准则的直线形式进行拟合，并得出等效的Mohr-Coulomb强度参数：

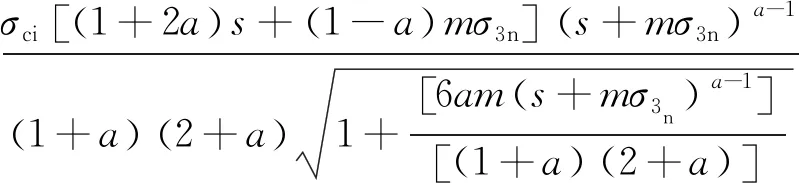
(2)

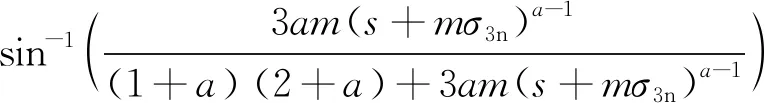
(3)

式中，σ3n=σ3max/σci，σ3max为侧限应力的上限值。

2 工程应用

2.1 工程概况

本次研究的边坡位于四川某石灰石露采矿区(图1)，矿区节理发育，规律性良好，其中以走向为NW—SE向节理最为发育，拟研究区域发育有5组优势结构面，倾角较缓。边坡开挖处露头呈现弱风化，岩体结构部分扰动。研究区采用小范围爆破与机械开挖方式，爆破效果较好。为了便于分析与建模，本节选取其中地质条件较为简单的1—1’剖面进行边坡稳定性分析(图2)。

图1 矿区场景图

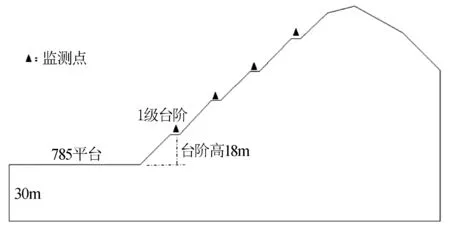
图2 简化1—1’剖面

2.2 岩体强度参数的选取

利用Hoek-Brown经验强度准则对岩体力学参数进行估算(表3、表4)，需要确定完整岩石的单轴抗压强度σci、完整岩石的Hoek-Brown常数mi、地质强度指标GSI、岩体扰动因子D。其中完整岩石的单轴抗压强度σci、完整岩石的Hoek-Brown常数mi可在室内试验的基础上获取，对于地质强度指标GSI、岩体扰动因子D的取值则需要结合现场地质情况结合表1和表2进行确定。

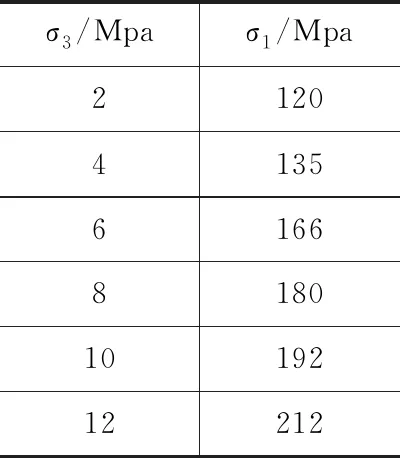
表3 三轴试验数据(天然工况)

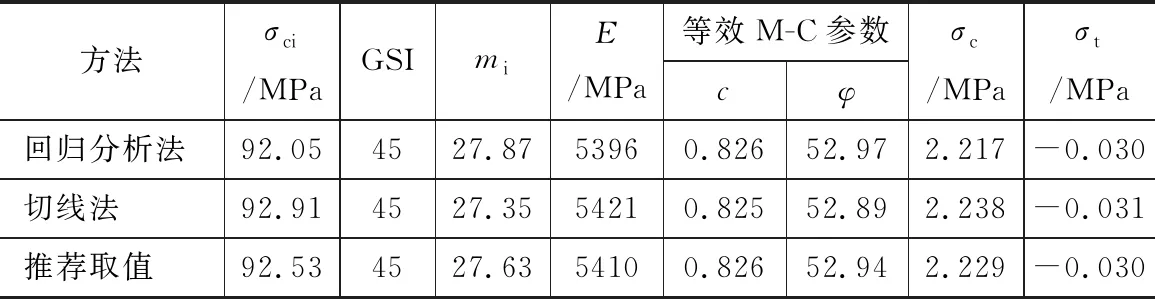
表4 Hoek-Brown强度参数

基于现场实际踏勘情况，结合Hoek等[5-6]提供的GSI围岩分级表和扰动系数取值建议表，GSI取值范围可定为40～60，取45；D取值范围为0.4～0.7，取0.7。结合Rocklab软件，分别采用线性回归法和切线法对Hoek-Brown经验强度参数的取值进行了比较，并在表4中给出了推荐值。

2.3 边坡稳定性数值模拟

通过已有的ANSYS-FLAC接口程序，按照剖面图建立有限差分法计算模型并在各台阶边坡处设置监测点，模型共10460个结点，4981个单元，在边坡坡脚和台阶处对网格细分，以提高计算精度。通过代入等效的岩体强度参数，结合强度折减法对边坡稳定性进行数值模拟分析。

2.3.1 位移云图

从X方向位移云图(图3)中可以看出，边坡最大位移分别出现在坡顶和坡脚处，最大位移值为0.3 cm。其中，坡顶处位移指向坡里，坡脚处位移指向坡外。从Z方向的位移云图(图4)可以看出，最大位移出现在坡顶，为2.1 cm，而坡脚处移基本上为0，各台阶处位移均较小。可认为边坡坡脚处存在挤出破坏的风险，而坡顶处存在局部坍塌的可能性，边坡总体处于稳定状态。

图3 X方向位移云图

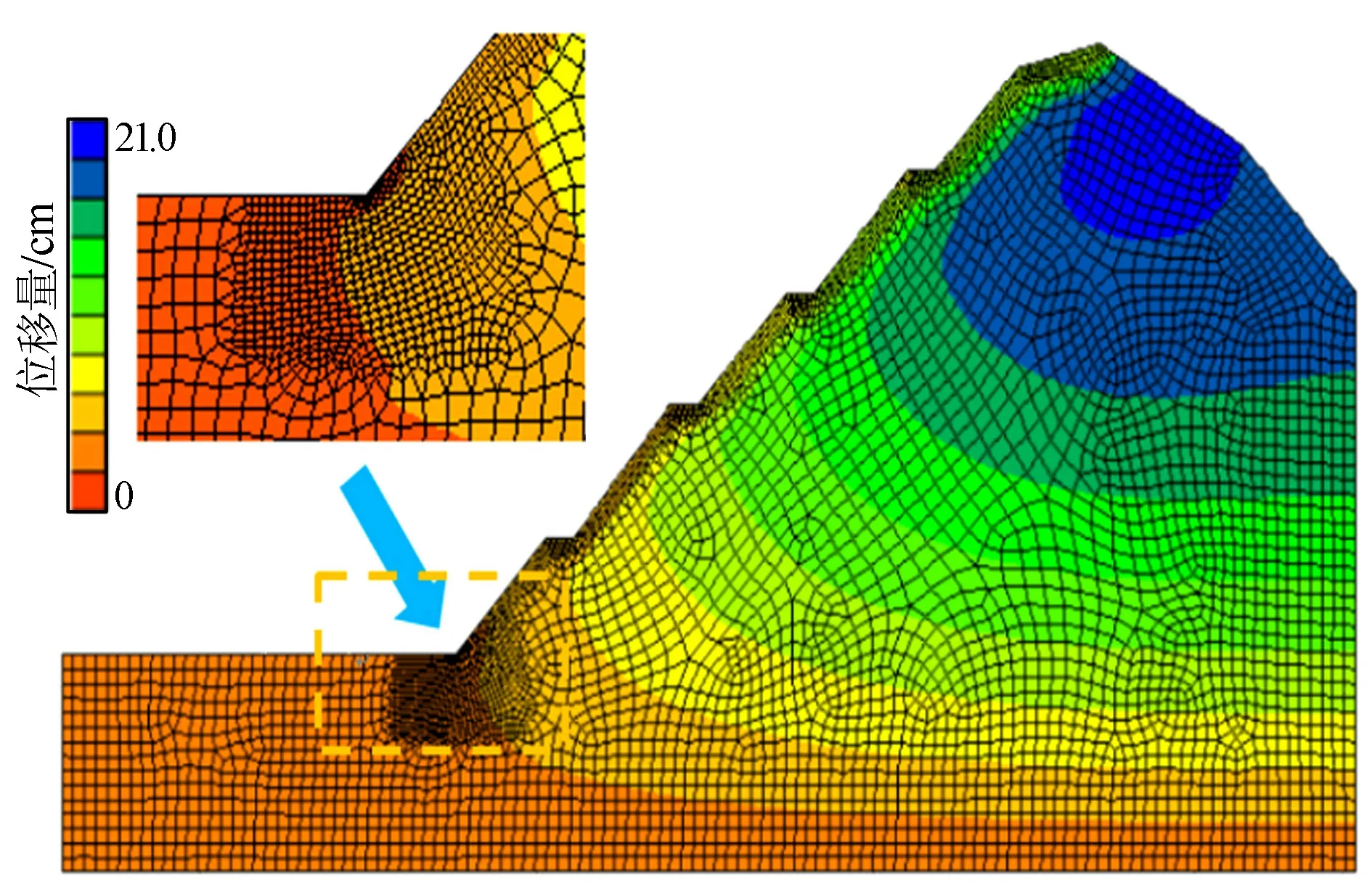
图4 Z方向位移云图

2.3.2 剪应变增量

由图5可见，最大剪应变增量出现在坡脚处，为1.75×10-3，而整体边坡整体剪应变增量基本为0。边坡台阶靠近坡面处剪应变增量较大，并且形成贯通的条带状结构，这表明坡脚和台阶处存在潜在危险，而实际在进行开挖施工时，坡脚处和台阶边坡上也出现了局部变形和崩塌。

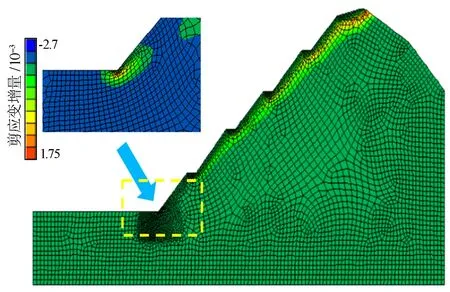
图5 剪应变增量云图

2.3.3 塑性区分布

由图6可见，目前边坡无塑性区，说明边坡整体稳定，但边坡出现相当大面积的拉伸破坏区，且在边坡上部台阶处贯通，这与实际明显不符，初步认定是由于岩体抗拉强度取值过小造成的，具体原因将在下文中进行分析。

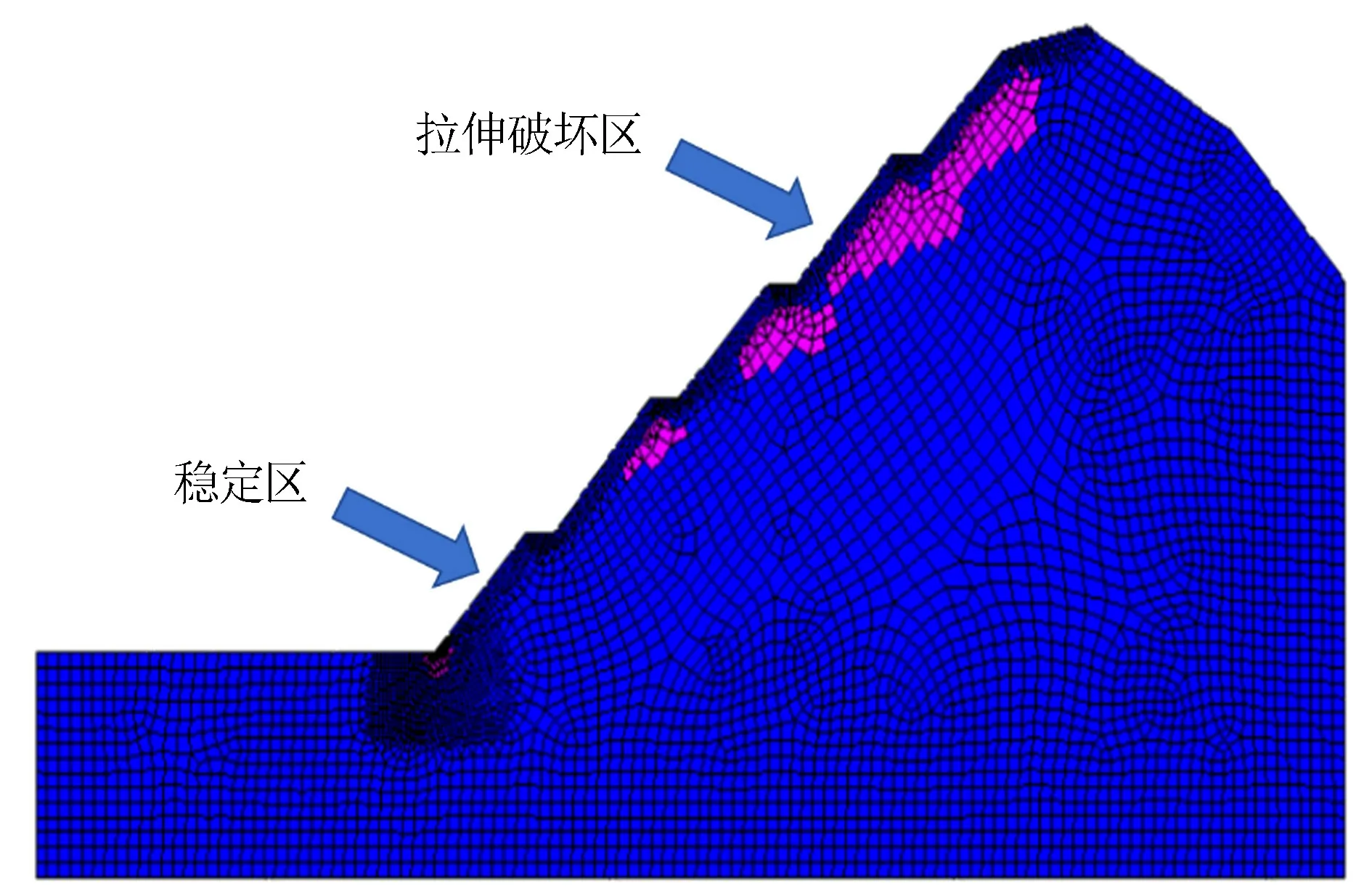
图6 塑性区分布

2.3.4 监测点位移

在建立模型时，在边坡坡脚及4个台阶处均设置了位移监测点，通过hist命令对监测点X方向位移进行记录。由图7可见，一级台阶顶部(即3#监测点)位移最大，为2.7 mm；而四级台阶顶部(6#监测点)位移最小，为1.3 mm，这与X方向位移云图相符。其他各监测点整体位移较小，说明边坡整体稳定。通过对等效摩尔库伦强度参数进行折减，得到该边坡整体稳定性系数为1.99，大于规范规定的矿山边坡安全性系数1.25，说明边坡整体稳定。

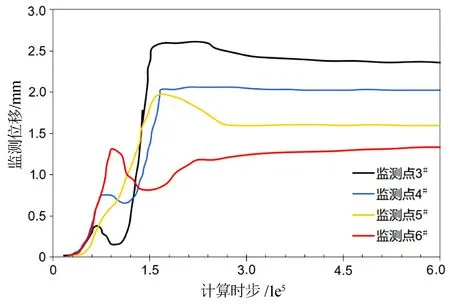
图7 监测点位移

通过对模型的以上参数进行分析，可以发现边坡主应力云图基本呈层状分布，应力集中效应不明显，边坡整体较稳定，但边坡局部位置出现应力集中现象，且位移较大，如边坡坡脚和台阶面处，可能出现局部破坏和坍塌。这与边坡实际情况较为符合。在矿区边坡进行露天开采时，一级台阶和二级台阶处出现边坡局部变形和垮塌，坡顶处出现明显局部变形，但边坡总体较为稳定。

2.4 分析与讨论

Hoek-Brown经验参数中完整岩石的单轴抗压强度σci和完整岩石的Hoek-Brown常数mi可通过室内岩石力学试验确定，可达到一个量化的评判标准，而在对地质强度指标GSI和岩体扰动因子D进行取值时，主要依据Hoek等[5-6]提供的GSI围岩分级表和扰动系数取值建议表，对露头岩体风化程度和爆破程度进行量化取值，十分依赖于现场人员的经验。黄高峰[14]基于试验数据和敏感性分析，将Hoek-Brown经验参数对岩体稳定性系数的敏感性进行了排序：GSI值>D>σci>mi。可见，GSI和D的取值对边坡稳定性分析有较大影响。

针对塑性区分布图(图6)中出现大面积拉破坏区的现象，本节选取强度指标GSI和岩体扰动因子D，分析其取值范围对岩体抗拉强度和等效的Mohr-Coloumb强度参数取值的影响。

2.4.1 GSI和D的取值对岩体抗拉强度取值的影响

对文中的矿山边坡的GSI值取45，D取0.7，通过Rocklab软件计算得岩体抗拉强度σt=-0.03MPa，而基于室内试验获取的岩体抗拉强度取值范围为-3.15 MPa～5.22 MPa，这两者相差极大。因此本小节综合考虑了GSI和D取值对抗拉强度的影响。由图8可见，当GSI值<75时，D对抗拉强度的影响占主要作用，且随着GSI值的增大，D的影响越大，但对抗拉强度的总体影响可以忽略。在这个范围内，岩体抗拉强度始终小于0.3 MPa。当GSI值>75时，GSI对抗拉强度的影响占主要作用。

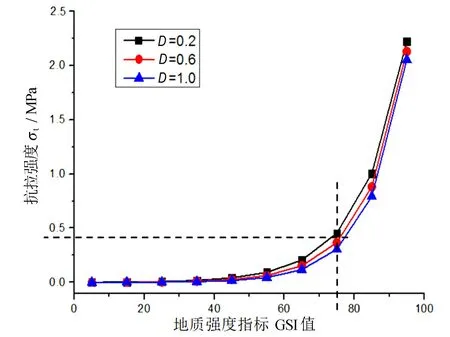
图8 经验参数对抗拉强度的影响

2.4.2 GSI和D的取值对黏聚力取值的影响

由图9可见，随着D值的增大，爆破扰动效应增大，且当GSI值在20～60之间时，D值影响最明显。当GSI值约为25时，D=0时的黏聚力约为4 MPa，而D=1时的黏聚力只有1 MPa，减小了约75%，可见岩体的开挖过程对岩体的内聚力影响很大。开挖扰动会导致岩体间咬合程度减弱，进而削弱其黏聚力的影响。

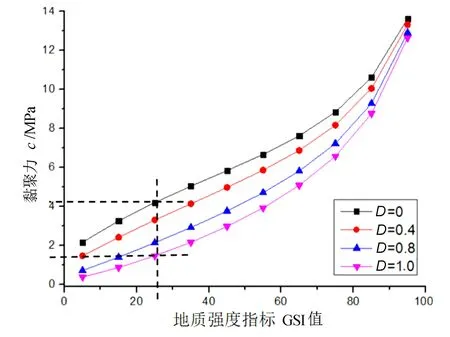
图9 经验参数对黏聚力的影响

2.4.3 GSI和D的取值对内摩擦角取值的影响

由图10可见，地质强度指标GSI的取值与内摩擦角的关系整体呈线性相关，随着GSI取值的增大，内摩擦角也不断增大，说明岩体结合越来越紧密。此外，扰动系数D对内摩擦角的影响很大，且随着GSI取值的增大，即随着岩体性质的改善，D对内摩擦角取值的影响越来越小，对于GSI值>90的岩体，当D的取值相差不大时，其影响基本可以忽略。

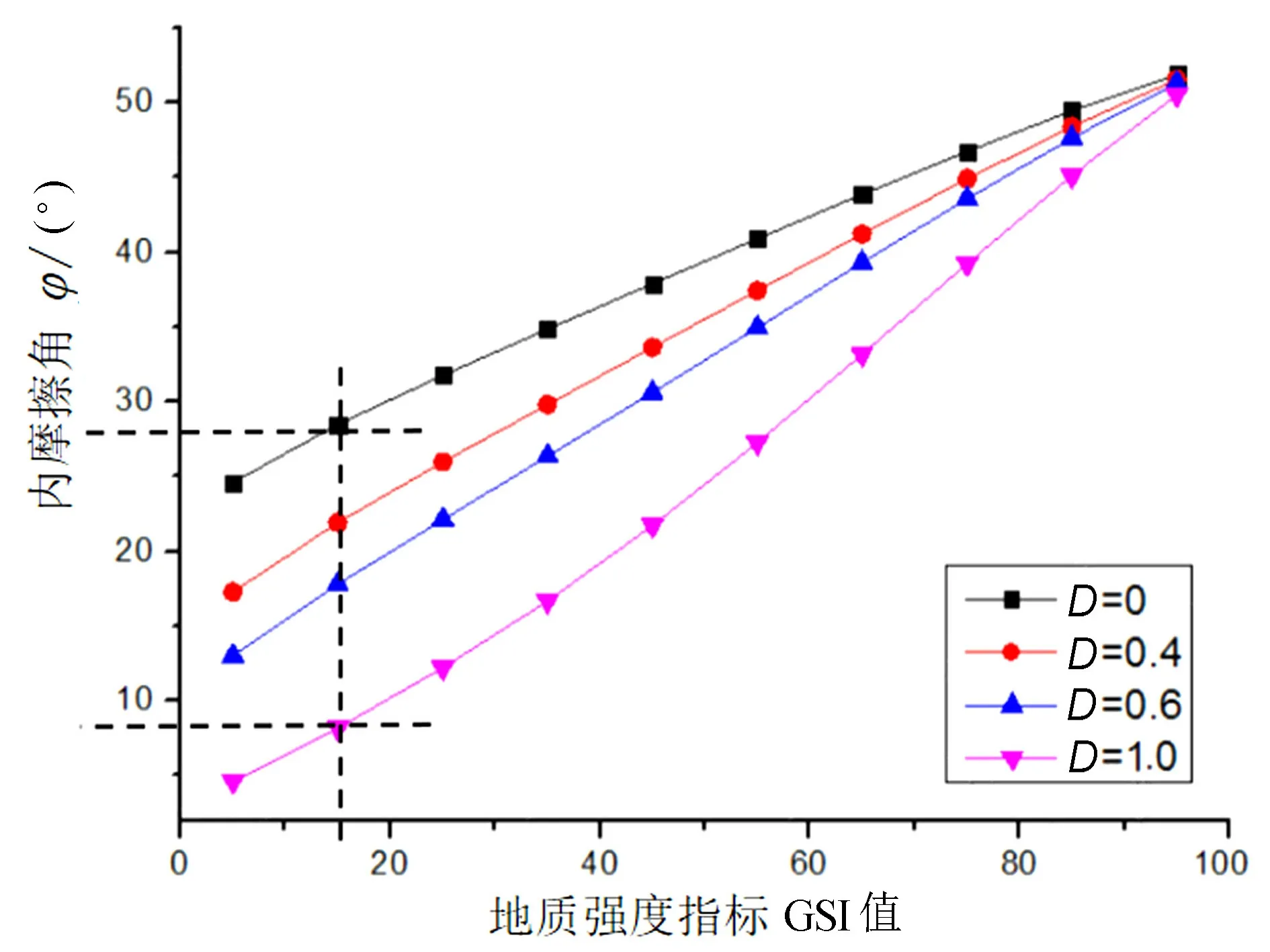
图10 经验参数对内摩擦角的影响

3 结论

本文结合某石灰石露采高边坡，运用Hoek-Brown强度准则对岩体强度参数进行选取，结合强度折减法对边坡稳定性进行数值模拟分析，并与现场监测情况对比，结果大致符合，表明了Hoek-Brown强度准则能很好地应用于岩体工程稳定性分析中。

参数敏感性分析结果表明，GSI取值对岩体抗拉强度的影响很大，且当GSI值小于某阈值时，抗拉强度的取值会极低，与实际情况不符，而扰动系数D的大小对内摩擦角取值影响更明显。因此，本文建议在进行Hoek-Brown强度准则参数取值时，应考虑不同对岩体强度参数的影响程度，确定一个参数区间，结合现场试验数据，比较两者权重，对岩体强度参数进行综合取值。