预应力混凝土连续梁桥悬臂现浇施工技术研究

王连乐

（中铁十八局集团第四工程有限公司，天津300000）

1 引言

在交通行业中，桥梁设施发挥着重要的作用。而随着经济的不断发展，初期使用的普通钢筋混凝土桥梁已经无法满足当前的交通需要，在此背景下预应力混凝土桥梁应运而生，其中因具备较大的刚度以及较大的跨度，预应力混凝土连续梁桥成为人们的首选桥型。

2 工程概况

双龙北线大偏坡大桥预应力混凝土连续梁桥全长178m，以挂篮悬臂的方式进行施工。桥梁下部构造采用的是圆端形实体桥墩，采用钻孔灌注桩作为其基础形式。具体桥跨结构如图1所示。桥梁在进行挂篮悬臂浇筑施工时采用的是先中跨后边跨的合拢方式，全桥合拢段共三个位置，长度均为2m。在主墩墩顶处进行临时支座的灌注之后在支架处进行0号块的灌注，再依次朝向两侧进行对称浇筑施工，从而形成悬臂T构，然后进行跨中位置中跨梁段的合拢以及进行不平衡段的悬臂灌注施工，最后通过钢管支架在边墩进行a12号梁段的浇筑施工以及边跨合拢段的浇筑，以使桥梁形成连续体系，将底板剩余钢束进行张拉并将支架进行拆除之后即可完成全桥的施工。

图1 桥梁布置图

3 施工控制

对于预应力混凝土连续梁桥而言，其整体的施工较为复杂。除了需要对称悬臂浇筑墩顶梁段之外，还需开展合拢段的施工并将临时固结进行解除以便进行体系的转换。因此在施工时随着施工的不断开展主梁的标高以及内力均在不断变化。对于桥梁的施工安全而言，桥梁合拢时的挠度和平面偏差均需满足一定的范围要求，而确保其处于范围内的最有效方法就是对施工全过程的施工监控［1］。通过施工监控反馈结果对施工过程进行不断的调整以确保桥梁施工的安全性。

对于桥梁的施工监控而言，当前最为常见的是自适应的控制方法，通过采集主梁标高以材料等数据，对实测数据的误差进行分析之后进行不断的修正，使实测值趋近计算值，从而对后续施工进行准确预估及控制的方法即施工监控。具体如图2所示。

图2 连续梁桥施工控制流程图

3.1 有限元分析

桥梁的施工控制主要依靠施工图纸及施工方案进行的。在开始施工之前，首先需要进行桥梁的初步计算，根据所得结果控制桥梁线形。本文以有限元分析软件Midas CIvil进行桥梁的建模处理，所得模型如图3所示。本桥梁模型包含有节点98个，梁单元73个。

图3 48m+80m+48m连续梁有限元模型

3.2 应力监测

基于该桥梁的特点，本次监测共确定6个监测断面，具体分布如图4所示。其中的危险截面为A，B，E和F截面。

图4 箱梁全截面应力测点断面布置图

基于对应力的测试后发现，混凝土受力之后产生的应力滞后性较大。并且滞后条件在较短的钢束条件下表现较不明显，而对于较长的弯曲钢束而言，其滞后的程度与张拉端有着较为紧密的联系，应力滞后情况在远离张拉端截面时越明显。

因篇幅所限，本文将仅列出部分关键数据，具体如表1所示。

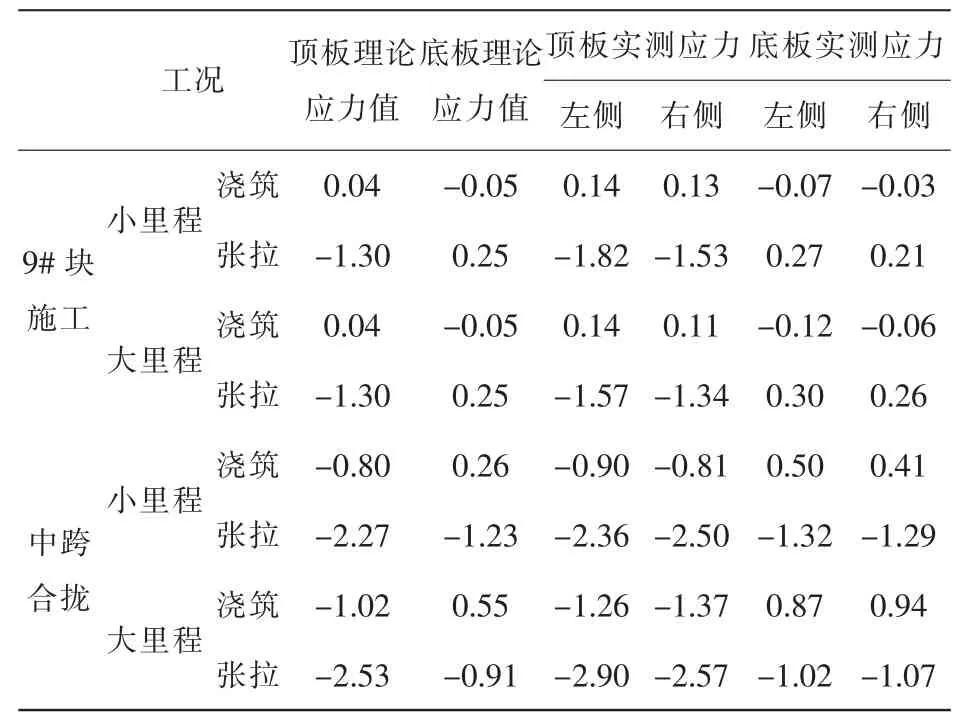
表1 跨中各施工阶段应力值（单位：MPa）

基于所得结果的对比分析可知，主梁截面的压应力随着不断增加的悬臂段长度而表现出不断的增长趋势，相比于理论应力而言，实测应力与其有着基本一致的变化规律。对于压应力而言，挂篮的前移以及混凝土的浇筑均会使顶板的压应力有所降低，并导致底板的压应力逐渐上升，施工时梁体的实测压应力有着-9.0mpa的最大值。对于该桥梁而言，其各个节块只通过顶板以及腹板的钢束进行连接，故在张拉预应力钢束时表现出不断增大的顶板压应力以及不断降低的底板压应力［2-3］。有限元计算结果和实测结果有着基本一致的变化规律，并且桥梁在施工时均保持在全截面受压的状态，表明桥梁有着较为稳定的施工状态。除去个别点的实测值和理论值有着较大的偏差之后，多数点位的实测值均与理论值较为接近，但整体上仍有较小的偏差，其原因主要在于： （1）混凝土材料是在实验室测定的弹性模量，相比于实际结构而言存在偏差，因此无法较好的反映出结构的实际应力值； （2）对于结构的应力而言，混凝土的收缩徐变对其存在一定的影响，但应力监控时若测点数据保持基本稳定，应力数值无异常的突变情况则可认为结构处于安全状态。总之，对于该连续梁桥而言，其在悬臂施工时各个截面的应力情况和理论值保持一致，各截面均满足受压的要求，有着较高的施工安全度。

3.3 位移监测

施工时需对各梁段挠度进行观测，并将所得数据进行处理之后提供给后续施工，以便于其对标高进行调整和控制，从而确保桥梁的线形满足要求［4］。基于现场的施工条件，在箱梁各个节段的纵向位置布置梁顶高程测点。具体位置如图5所示。按照设计要求安排监测工况，若因现场条件有限不得不改变施工阶段，则需对其进行灵活的调整。对于挂篮悬臂浇筑的施工阶段而言，其施工周期为挂篮前移到张拉预应力筋之后，在该施工周期内，应在浇筑完混凝土与张拉完预应力钢筋之后对其位移进行观测。

图5 截面测点布置示意图（单位：cm）

基于设计图纸所确定的梁段尺寸以及所用材料即可对各施工阶段的累计挠度进行分析。而将该挠度进行反号之后即可以得到预拱度，在此基础上将荷载作用下的挠度以及挂篮弹性变形进行叠加即可设置预抛高。对于桥梁线形而言，预抛高的设置对其有着较大的影响。

对于梁体变形而言，结构自重参数的选取是否合理对其有着较大的影响［5］。而对于结构自重而言，混凝土容重以及结构尺寸是重要的影响因素。在计算模型中将结构的体系和混凝土容重进行相乘再与自重系数做一次乘积即可作为结构自重的参数。在本模型中，以25KN/m3作为素混凝土的容重，基于对普通钢筋所处贡献的考虑，选取-1.05作为其自重系数。以跨中墩在最大悬臂状态下的情况为例，可得其自重荷载的变形情况如图6所示。

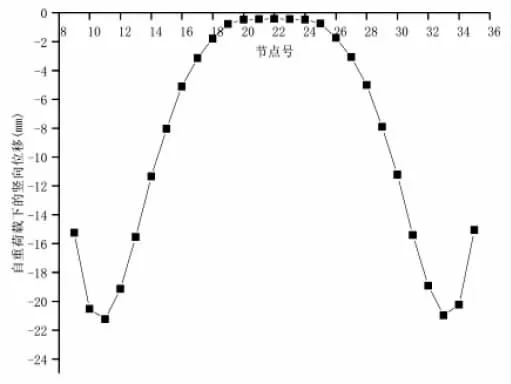
图6 自重荷载下最大悬臂状态的位移情况（单位：mm）

从图中可知，随着不断增加的悬臂长度梁体在自重荷载下有着不断增加的位移，在两侧悬臂浇筑段的端头出现了极大值，并且在悬臂端部不断减小，因仅有几个块段对悬臂端部梁段有所影响，因此其挠度随着悬臂状态的增大而有所降低。

同理，对预应力荷载作用下的变形进行分析可知，在预应力的作用下支座处节点位移为零，张拉的钢束随着不断增加的悬臂段逐渐增加，并且在墩顶两侧变形逐渐增加［6］，在端部又趋于降低，在7号块处有着最大的跨中变形。

综合上述多种影响因素之后，根据预拱度计算公式进行计算：

式中：Hlmi为第i节段立模标高；Hsji为第i节段设计标高；f为第i节段所需预拱度值。

计算结果如下图所示。

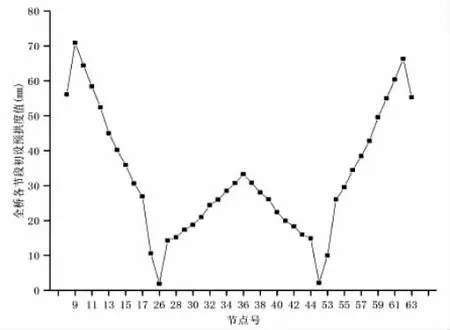
图7 悬臂段各节点累计预拱度（单位：mm）

基于现场监测数据可知，该桥梁的挠度以一定规律进行变化。对比中跨合拢之后的挠度实测值和理论值，可得如图8所示结果。

图8 边跨不平衡段浇筑后挠度对比示意图

在浇筑完不平衡段之后，相比于理论值而言，其实测值较大，约有1cm的偏差，对其原因进行分析可知，在不平衡梁段的同步配重施工时，因所配置的机械问题，导致其在完成浇筑之后未能及时施工预压块，导致在完成浇筑的两个小时之后才使配重达到设计重量要求。但对其所得的整体挠度可知，该桥梁的挠度控制较为合适，在合拢段的浇筑施工时，两端仅存在2cm以下的高差，满足精度要求。

4 结语

本文根据某桥梁的监测施工，对其整体流程进行了详细的分析研究。在现场实际的基础上，对各项参数进行及时的识别和修正，基于此次分析，也从另一角度验证监测模型对于连续梁监测的合理性。通过对桥梁施工阶段数据的全面分析，对其梁段施工时的线形发展进行了控制，使其线形保持在较为理想的状态，表明对于主梁的位移而言，施工监控取得的效果较好。通过对悬臂浇筑施工阶段截面的应力进行分析可知，其压应力保持着规律性的变化，并在最终使得梁体保持在全截面受压状态，使结构处于安全状态。