Variable Selection and Parameter Estimation with M-Estimation Method for Ultra-high Dimensional Linear Model
2021-10-20ZHUYanling朱艳玲WANGKai汪凯ZHAOMingtao赵明涛
ZHU Yanling(朱艳玲),WANG Kai(汪凯),ZHAO Mingtao(赵明涛)
(School of Statistics and Applied Mathematics,Anhui University of Finance and Economics,Bengbu 233000,China)
Abstract:In this paper,the variable selection and parameter estimation of linear regression model in ultra-high dimensional case are considered.The proposed penalty likelihood M-estimator is proved to have good large sample properties by unifying the least squares,least absolute deviation,quantile regression and Huber regression into a general framework.The variable selection and parameter estimation are performed best by combining backward regression with local linear regression in the numerical simulation.In the case of ultra-high dimension,our general method has good robustness and effectiveness in variable selection and parameter estimation.
Key words:Ultra-high dimensionality;M-estimation;Penalized likelihood;Variable selection
1.Introduction
For the classical linear regression modelY=Xβ+ε,whereY=(y1,y2,...,yn)Tis the response vector,X=(X1,X2,...,Xpn)=(x1,x2,...,xn)T=(xij)n×pnis ann×pndesign matrix,andε=(ε1,ε2,...,εn)Tis a random vector.When dimensionpnis high,it is often assumed that only a small number of predictors among all the predictors contribute to the response,which amounts to assuming ideally that the parameter vectorβis sparse.In order to implement sparsity,variable selection can improve the accuracy of estimation by effectively identifying the subset of important predictors,and also enhance model interpretability of the model.




In this paper,we assume that the functionρis convex,hence the objective function is still convex and the obtained local minimizer is global minimizer.In Section 2,we discuss some theoretical properties of LLA estimator.In Section 3,we supply a simple and efficient algorithm to give the numerical simulation results.The proofs are given in Section 4.
2.Main Results


3.Simulation Results
In this section we evaluate the performance of the M-estimator proposed in(1.1)by simulation studies.


For the RSIS+LLA method,it tends to make a more robust selection in the first step,and performs well on the two indicators of estimation error and prediction error,but thus loses part of the ability to misidentify important variables,which makes it easy to omit important variables and cause great errors.In fact,we can guarantee the robustness of the selection and estimation by using the LAD loss function in the second step variable selection.
For the HOLP+LLA method,its performance in the three indicators of prediction error,correct exclusion of unimportant variables,and error identification of important variables is almost equal to that of FR+LLA,but it is slightly worse in the estimation error of the first index.
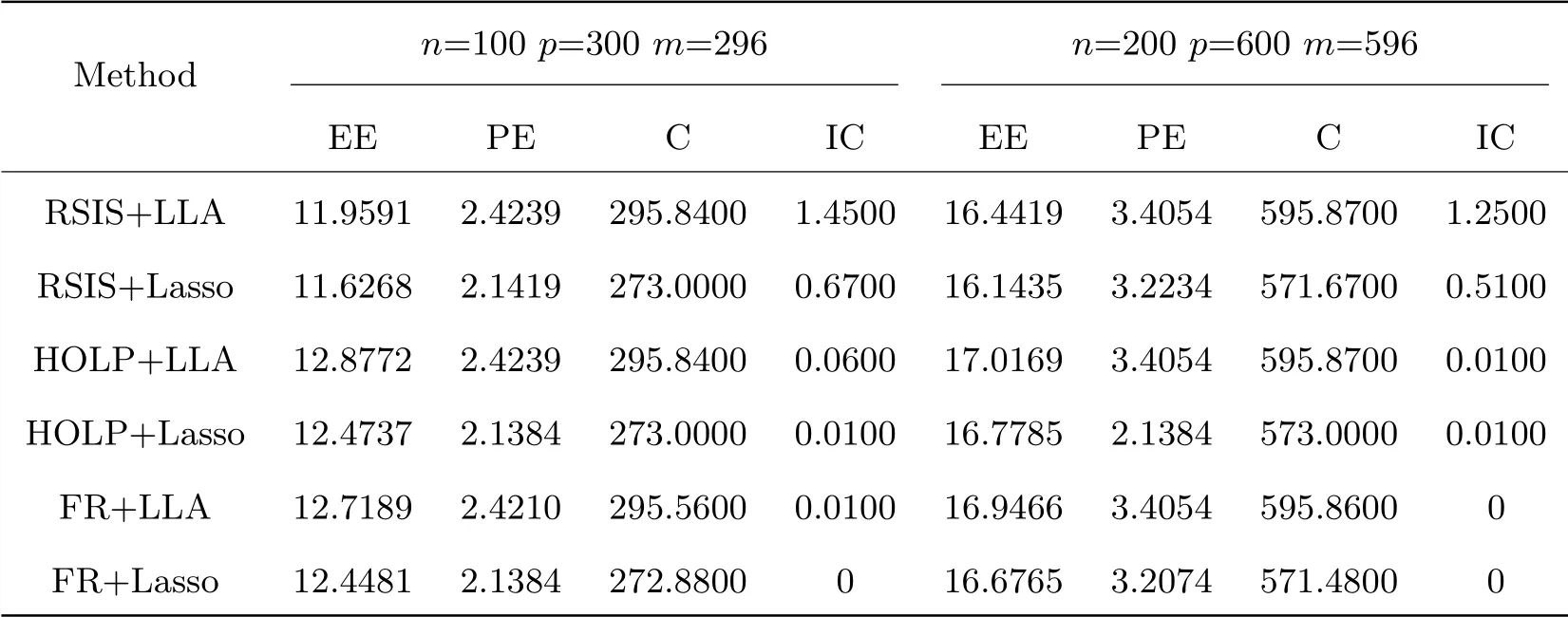
Tab.1 Numerical Results for ε ~N(0,1)
Example 2 We consider the case of the LAD loss function and the error termε ~t5.The estimated results are shown in Tab.2.
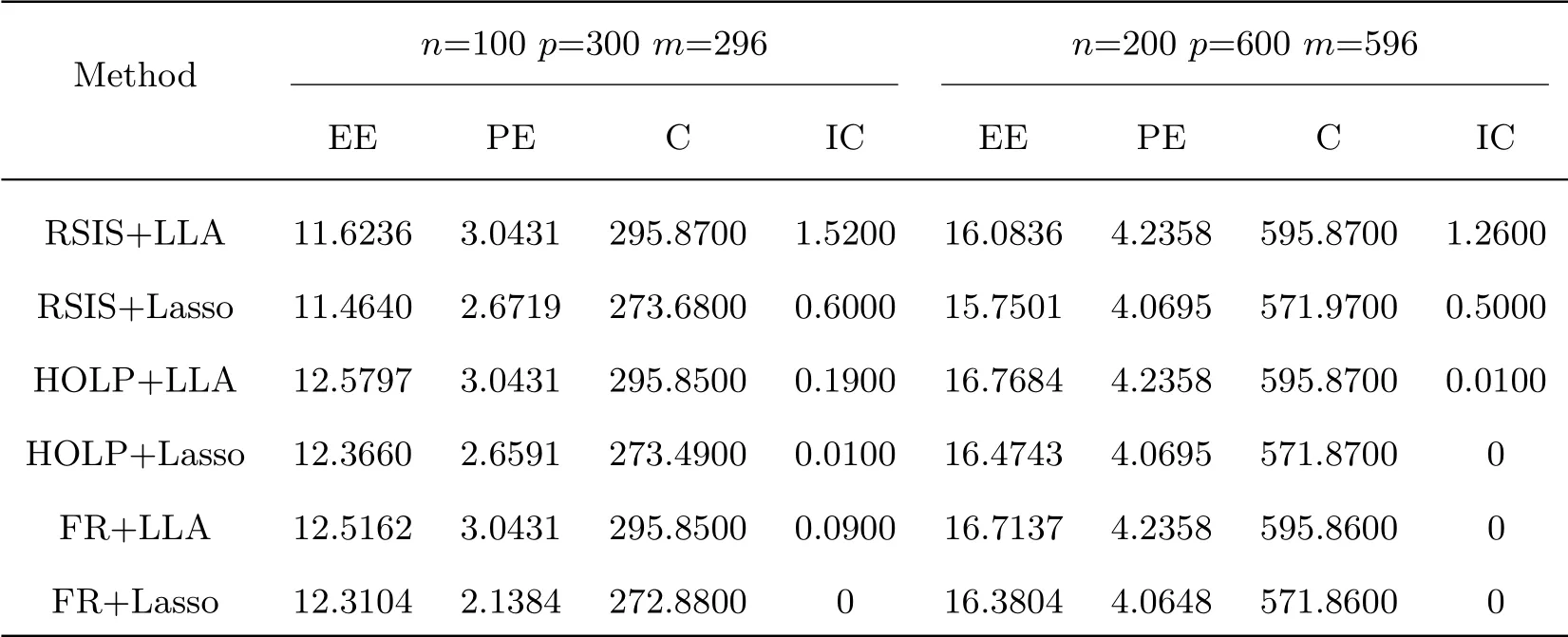
Tab.2 Numerical Results for ε ~t5
When the selection error term follows the heavy-tailed distribution,all six methods in Tab.2 perform better than the error term of the standard normal distribution in the first index estimation error and the third index correctly excluding the unimportant variable.The second indicator is slightly worse than the forecast error,and the fourth indicator is basically flat.Overall conclusion is consistent with Example 1,i.e.the performance of the FR+LLA method is slightly superior.
Example 3We consider the case of the LAD loss function and the error termε ~0.9N(0,1)+0.1N(0,9).The estimated results are shown in Tab.3.
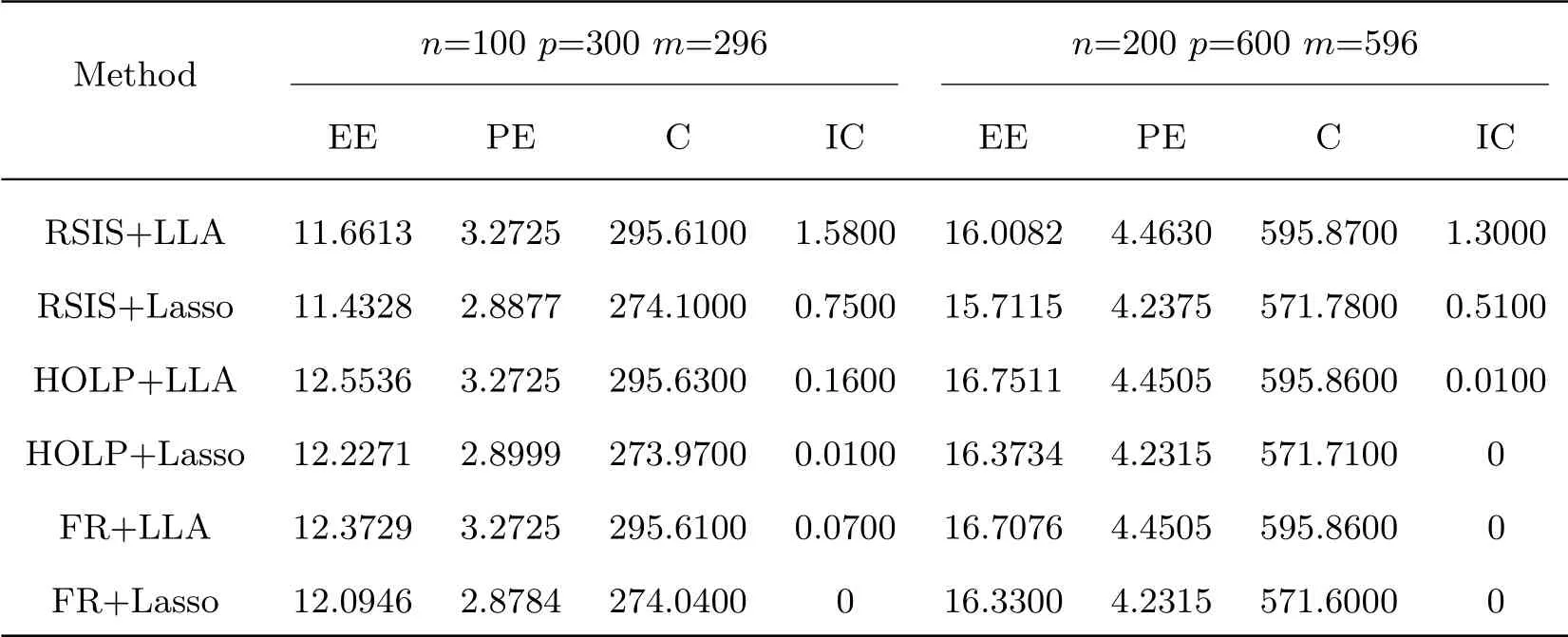
Tab.3 Numerical Results for ε ~0.9N(0,1)+0.1N(0,9)
Synthesizing simulation results from Example 1 to Example 3,it can be seen that in the case that the number of explanatory variables is larger than the sample size,we design the plan that the backward regression FR method is used in the first step of variable screening,and the second step uses the local linear penalty LLA method proposed,and the performance on the four indicators is quite good.It also shows that for ultra-high dimensional data models,using the screening method of FR+LLA we provide is feasible and effective,and can be applied to more extensive data to obtain more satisfactory results.
4.Proofs of Main Results

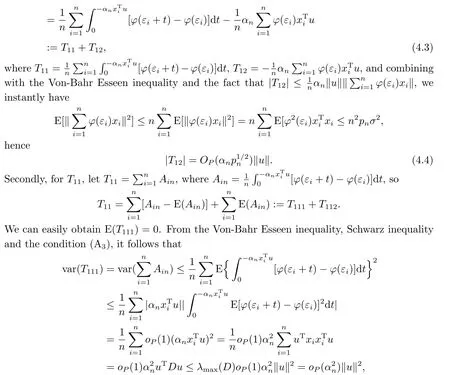



杂志排行
应用数学的其它文章
- Global Boundedness and Asymptotic Behavior in a Chemotaxis Model with Indirect Signal Absorption and Generalized Logistic Source
- Performances of Preliminary Test Estimator for Error Variance Under Pitman Nearness
- 一类梯度自然增长的拟线性椭圆型方程分布正解的存在性与多重性
- 一类由原根生成的伪随机子集
- 混合次分数布朗运动下永久美式回望期权的定价
- 双水平控制策略和延迟不中断单重休假的M/G/1排队系统分析
