混合次分数布朗运动下永久美式回望期权的定价

2021-10-20安翔郭精军

应用数学 2021年4期

安翔,郭精军

(兰州财经大学统计学院,甘肃兰州730020)

1.引言

随着金融市场的快速发展,期权作为一种金融衍生品应运而生,因其具有规避风险与投资保值的功能,受到了许多投资者的青睐.回望期权[1]是一种强路径依赖期权,即期权的收益不仅依赖于到期日当天标的资产的价格,而且依赖于整个有效期(称为回望期)内标的资产价格的变化幅度.该期权给予持有者“低买高卖”的权利,这是期权持有者梦寐以求的情形,他可以选取回望期内最低(高)的标的资产价格,买入(卖出)标的资产.由于持有者始终处于最有利的位置,这保证了他可以得到较高的收益,从而回望期权的价格也十分昂贵.因此,回望期权的定价一直是期权定价中的热点话题之一.

近年来,金融机构为了满足不同市场的各种需求,衍生出了许多新型期权,美式回望期权就是其中一种.该期权是一种具有回望特征的美式期权,相对于传统的美式期权,其收益更高.众所周知,美式期权的定价是一个非线性问题,除了永久美式期权,一般不存在闭式解.因此,美式回望期权的定价问题常用数值方法求其近似解[2−3].为了更好地研究美式回望期权,DAI[4]提出了永久美式回望期权,其收益与时间无关,只依赖于回望期内标的资产价格的最值;并给出了该期权价格的闭式解与最优实施边界,这可作为研究美式回望期权的一个基本框架,用于对美式回望期权的价格进行近似计算.除此之外,永久型期权还可以应用于各种金融问题,譬如与实物期权相关的最优投资时机问题[5].因此,对于永久美式回望期权的研究具有一定的现实意义.

然而,上述的研究都是在经典的Black-Scholes模型(以下简称B-S模型)下进行的,即都假设标的资产的价格变化服从几何布朗运动.但是,对于金融市场的大量实证研究表明:金融资产对数收益率的分布呈“尖峰厚尾”状,并不服从正态分布,而且金融资产的价格变化具有长相依、自相似等分形特征,几何布朗运动无法刻画这些特征.因为分数布朗运动能够较好地刻画这些分形特征[6],所以为了改进经典的B-S模型,有学者用分数布朗运动驱动B-S模型的随机部分[7−8].

但是,分数布朗运动不是半鞅,直接将其应用于金融模型中会产生套利机会.为了刻画长相依、自相似等特征,并消除套利机会,一些学者提出用混合分数布朗运动或混合次分数布朗运动代替分数布朗运动.目前,基于混合分数布朗运动研究期权定价的文献较多.[9−11]与混合分数布朗运动相比,混合次分数布朗运动不仅具有长相依、自相似等特征,而且还具有非平稳的二阶矩增量,从而混合次分数布朗运动能更好地刻画金融资产价格的变动.Charles等[12]证明了Hurst指数H ∈[0.75,1)时,混合次分数布朗运动具有长相依、自相似等特征,并且是一个半鞅,此时,由混合次分数布朗运动驱动的金融市场是完备的.郭精军等[13]基于混合次分数布朗运动,给出了永久美式期权的定价公式及其最优实施边界.

为了更好地刻画标的资产价格的变化趋势,本文对文[4]中的模型进行改进.在考虑标的资产带红利的基础上,结合混合次分数布朗运动,建立了混合次分数布朗运动下带红利的永久美式回望期权的定价模型,得到了该期权的定价公式和最优实施边界.行文安排如下:第2部分介绍相关的预备知识;第3部分建立定价模型;第4部分给出该期权价格的闭式解与最优实施边界;第5部分为数值实验;第6部分为结论.

2.预备知识

3.定价模型

Ⅰ 模型假设

假设金融市场中存在两种可自由连续交易的资产:无风险资产Bt(如债券)和风险资产St(如股票),并满足以下条件:

1)市场是无摩擦的,即交易费用为零,无税收;

4.模型求解

zη是方程λ2(1−λ1)z2θ+1+λ1λ2z2θ −λ1(1−λ2)z −λ1λ2=0在(0,1)内的唯一解.

证明过程与定理4.1类似.

5.数值实验

以永久美式回望看跌期权为例,根据定理4.1,运用R语言与MATLAB软件,进行数值实验.首先,考察x与y等比例变化时,对定价结果的影响.为此,将部分参数设为

r=0.5,q=0.05,H=0.75,σ1=0.2,σ2=0.3,t=1.5,

取标的资产价格x= 5,标的资产价格的最大值y=6,将x与y等比例放大,运用R语言作出V(x,y)的散点图,如图5.1所示.

图5.1 永久美式回望看跌期权价格的线性等比例放缩性质

由图5.1可以看出当x与y等比例变大时,永久美式回望看跌期权价格V以相同的比例变大.这表明在混合次分数布朗运动环境下,永久美式回望看跌期权的价格V具有线性等比例放缩性质[14],即对于任意的非负常数a,有

V(ax,ay)=aV(x,y).

这种变化趋势符合实际情况,从而说明了该定价公式的正确性.

然后,考察Hurst指数对永久美式回望看跌期权价格的影响.为此,固定y= 6,取标的资产价格x ∈[5.75,6),Hurst指数H ∈[0.75,1),其余参数保持不变.运用MATLAB软件作图,如图5.2所示.

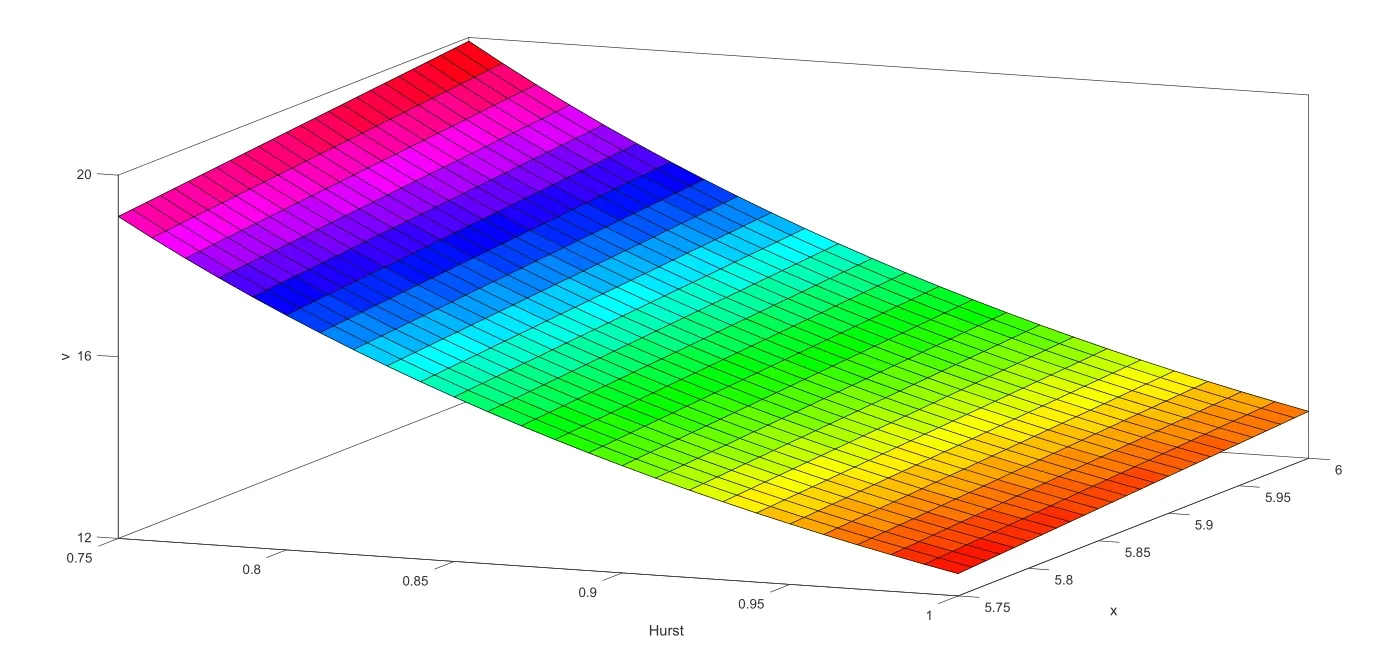
图5.2 永久美式回望看跌期权价格随Hurst指数变化图

图5.2描述了当Hurst指数H ∈[0.75,1)时,永久美式回望看跌期权的价格V随着Hurst指数的变化情况.该图表明,在混合次分数布朗运动环境下,随着Hurst指数的增大,永久美式回望看跌期权的价格V不断减小.这种变化趋势符合实际情况,因为当Hurst指数增加时,标的资产价格的路径会更光滑,即价格波动变小,此时,期权带来的回报就会降低,从而导致期权价格下降.

最后,在波动率σ1与σ2取不同值的情况下,考察标的资产价格增加时,永久美式回望看跌期权的价格变化情况.为此,固定y= 6,令x ∈[5,6),分别取σ1= 0.20,σ2= 0.30;σ1= 0.25,σ2= 0.35;σ1= 0.30,σ2= 0.40;σ1= 0.35,σ2= 0.45;σ1= 0.40,σ2= 0.50.其余参数不变,运用MATLAB作图,如图5.3所示.