求解非线性脉冲延迟微分方程的高阶数值方法

龙滔,余越昕

(湘潭大学数学与计算科学学院,湖南湘潭411105)

1.引言

科学与工程中的许多实际问题,其发展过程会受到瞬时突变的影响,也即系统的状态在某些时刻会产生瞬时跳跃,这种现象称为脉冲现象.另一方面,系统状态的变化不仅与当前状态有关,还依赖于过去状态,即受时滞的影响.当系统同时受到脉冲和时滞影响时,其数学模型一般为脉冲延迟微分方程,在物理学、生物学、医学、经济学以及控制系统等众多科学与工程领域有广泛应用.

脉冲延迟微分方程相关理论的研究可参见文[1-8].由于脉冲延迟微分方程的理论解一般很难获得,因此其数值方法的研究就显得尤为重要.2010年DING等人在文[9]给出了求解线性脉冲延迟微分方程定步长的Euler方法,并且证明了方法是1阶收敛的.对于一类线性脉冲延迟微分方程,文[10-12]将其转化为无脉冲的延迟微分方程,分别研究了Runge-Kutta方法和线性多步法的稳定性.2017年ZHANG在文[13]将Runge-Kutta方法用于求解非线性脉冲延迟微分方程,并研究了方法的收敛性.2019年LI等人在文[14]将再生核方法用于求解分段常数的线性脉冲延迟微分方程,并证明了方法是收敛的.

经典的block-by-block数值方法对于积分方程的求解是非常有效的,2016年马群长等人[15]将其用于求解脉冲微分方程并研究了方法的收敛性和稳定性.同年,曹俊英等人[16]构造了求解脉冲微分方程的修正的block-by-block方法,并证明了方法是4阶收敛的.本文利用文[16]的思想,构造了求解非线性脉冲延迟微分方程的高阶数值格式,通过收敛性分析证明了其是4阶收敛的,最后的数值试验也验证了该理论结果.

2.数值方法的构造

3.收敛性分析

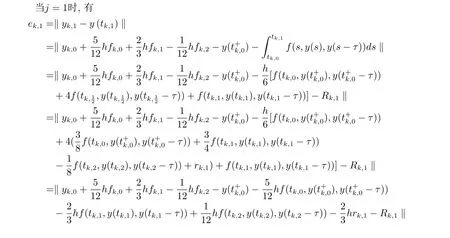
4.数值试验

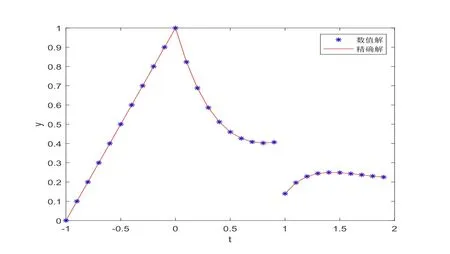
图4.1 h=0.1时,应用数值方法(2.12)求解例4.1的数值解与精确解

对问题(4.2)取步长h=0.01,利用数值方法(2.12)求解所得到的图形如图4.2所示.

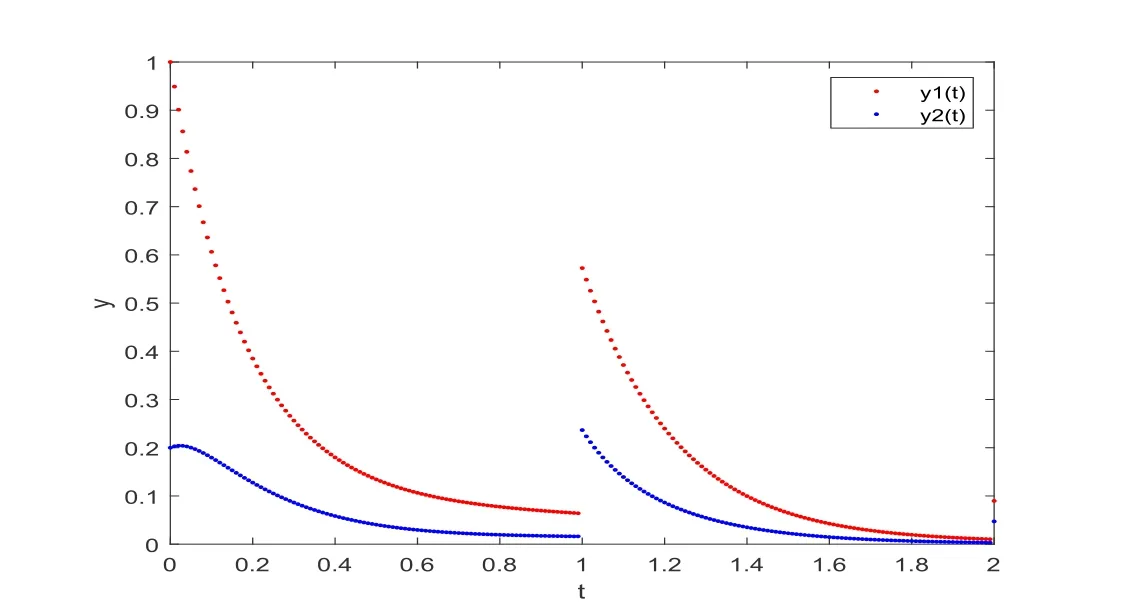
图4.2 h=0.01时,应用数值方法(2.12)求解例4.2的数值解

为了更好的刻画数值格式(2.12)的精度,针对例4.1我们采用最大绝对误差,即max|yk,j −y(tk,j)|(k= 0,1,2,··· ,n,j= 0,1,2,··· ,m),相关结果如表4.1所示.针对例4.2,我们采用在∞范数意义下的全局绝对误差来刻画数值格式(2.12)的精度,由于例4.2的真解无法求出,这里取时的数值解近似代替真解,相关结果如表4.2所示.

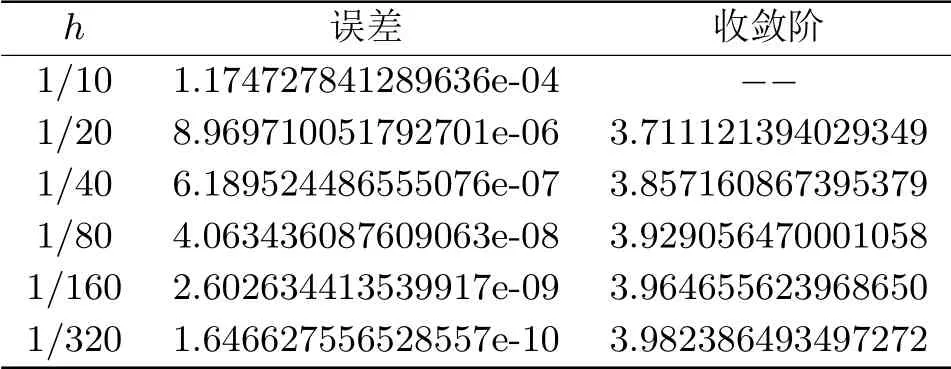
表4.1 求解例4.1的最大绝对误差与收敛阶

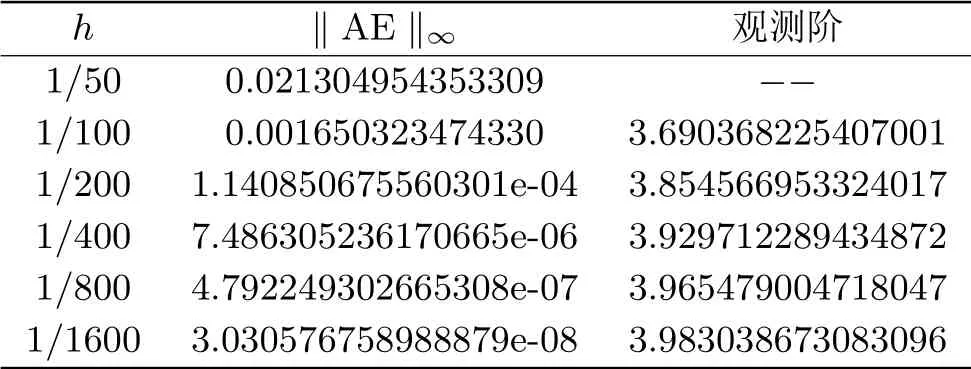
表4.2 求解例4.2的全局绝对误差(‖AE‖∞)与观测阶

从表4.1、4.2可以看出,最大绝对误差和‖AE‖∞随着步长h的减小而减小,并且收敛阶或观测阶都接近于4,这与我们的理论分析一致,从而说明我们所构造的数值方法(2.12)具有高阶收敛性.