线性分式多乘积问题的ϵ-近似算法

申子慧,陈玉松,申培萍

(1.商丘工学院基础教学部,河南商丘476000;2.华北水利水电大学数学与统计学院,河南郑州450000)

1.引言

2.问题的等价转化

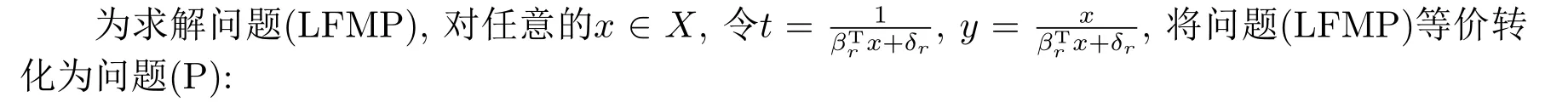
3.算法理论基础

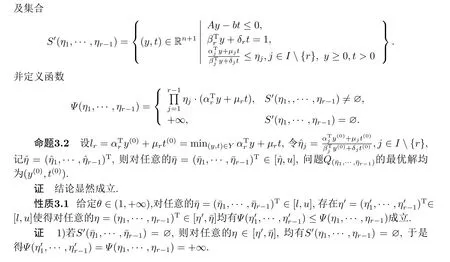
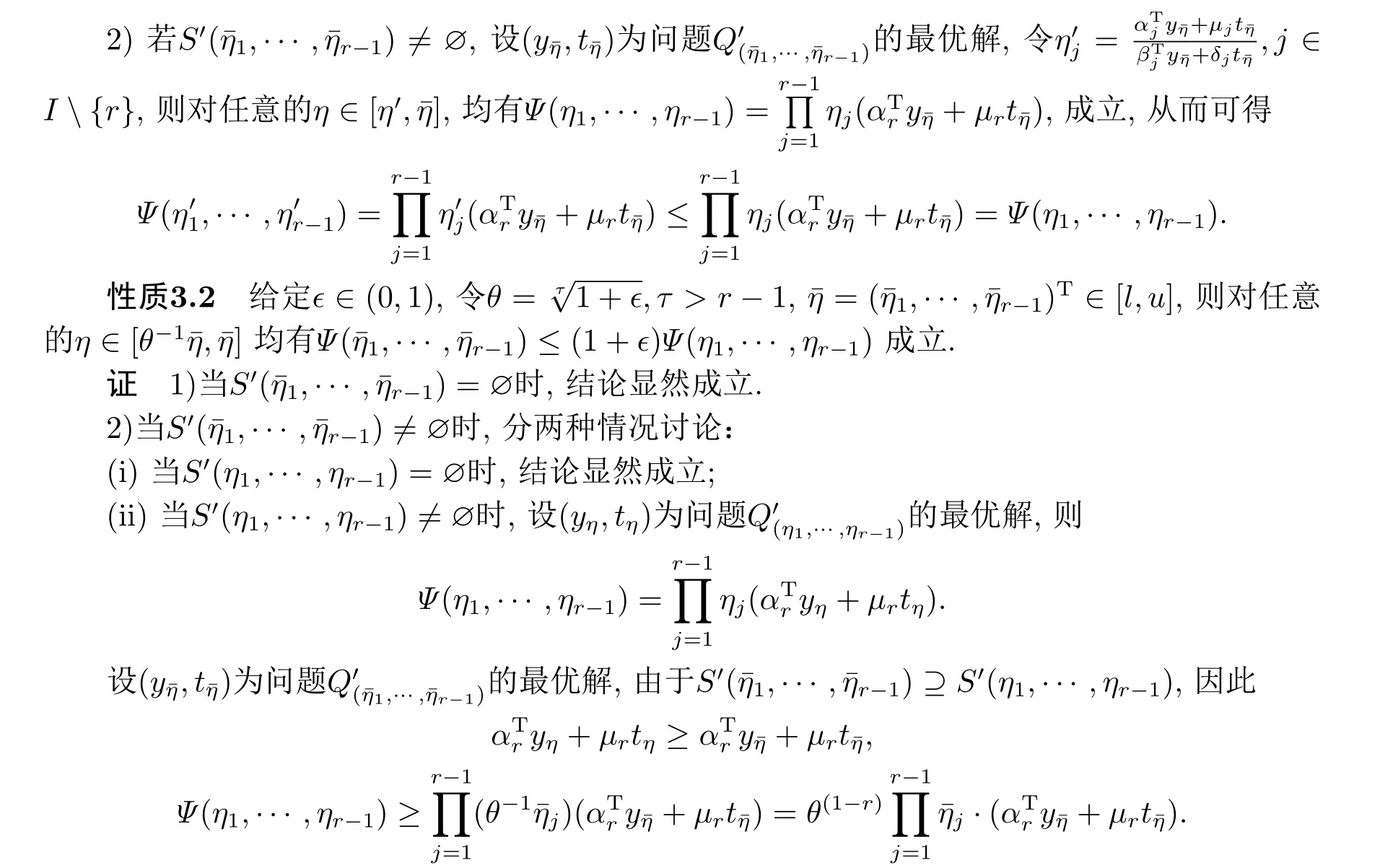
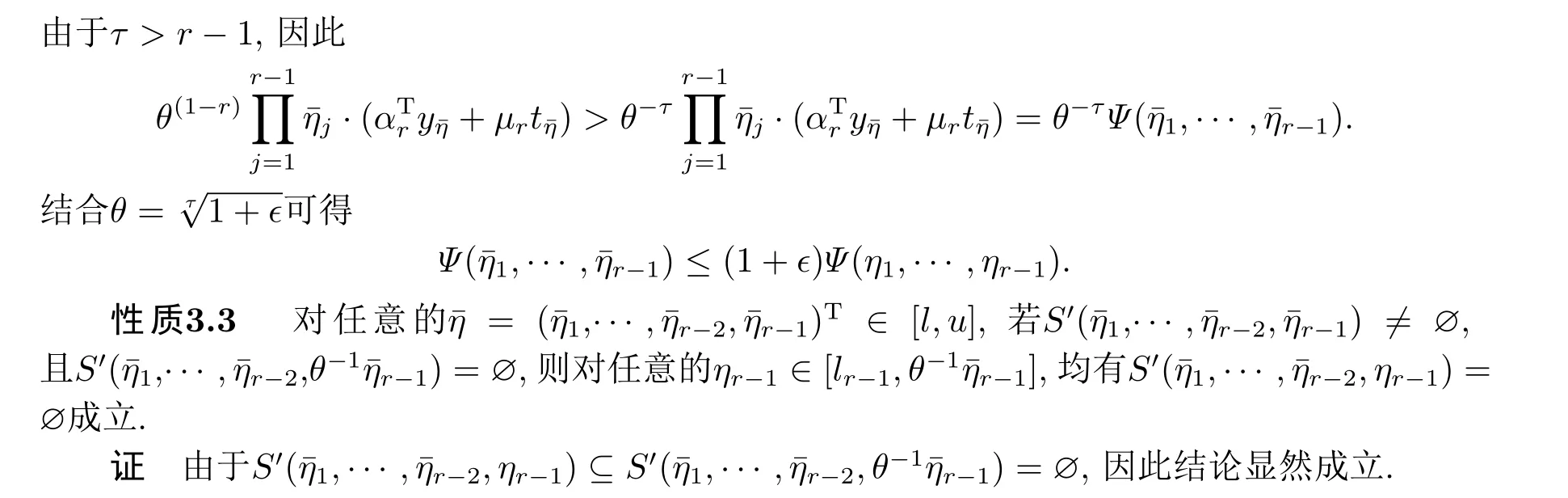
4.(1+ϵ)-近似算法

5.计算复杂度

6.数值算例

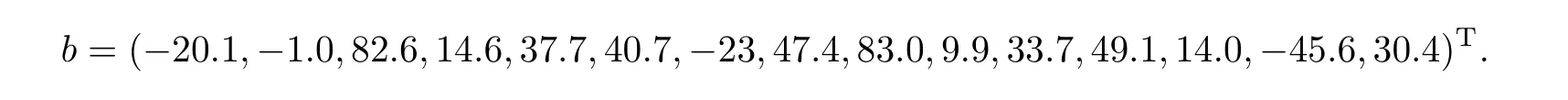
给定ε= 0.12,τ= 3,本文计算结果:最优解为(0.0000;1.3866;7.2004;2.8519;4.6240;0.0000;0.0000;5.6716;0.0923;4.2396;4.5181;5.3483),近似最优值0.2687,最优值上界为0.2687,运算时间为7.1930秒.

给定ε=0.12,τ=3,文[6]计算结果:最优解为(0.0052;1.3800;7.1955;2.8451;4.6285;0.0000;0.0000;5.6634;0.0975;4.2355;4.5208;5.3534),近似最优值0.2687,最优值上界为0.2716,运算时间为293.3500秒.