基于Lagrange 及SPH 算法的花岗岩侵彻数值模拟

靳绍虎，刘科伟，黄 进，杨家彩，靳少博

（中南大学资源与安全工程学院，湖南 长沙 410083）

自海湾战争以来，随着精确制导武器和小型钻地核武器的不断发展，地下防护空间的开发利用也在世界各国的国防建设中得到普遍发展，并受到高度重视[1]。岩石作为一种天然的防护材料，具有强度高、硬度大、弹性模量大等优点，被广泛应用于防护工程和重要军事设施的构筑。在过去的几十年里，国内外专家学者对于岩石靶体的侵彻效应进行了深入研究，依据不同研究手段，分为实验[2-5]、理论[6-9]和数值模拟研究[10-13]。

近年来，随着计算机技术的发展，数值模拟凭借其经济性、高效性和准确性，逐渐被学者应用于侵彻问题的研究。Warren 等[10]建立了弹丸和石灰岩靶体的有限元模型，对斜侵彻过程中弹道轨迹进行预测，与室内实验结果基本吻合。Tham[11]采用Lagrange、Euler-Lagrange 耦合和SPH-Lagrange 耦合3 种方法模拟弹体侵彻过程，预测混凝土靶体的最大侵彻深度以及径向应力-时间的关系。强洪夫等[12]进一步优化了SPH（Smooth particle hydrodynamics）算法，用于花岗岩目标的碰撞侵彻研究，给出了成坑深度与侵彻速度的关系式。在侵彻过程中，材料往往处于高应力、大变形状态，采用Lagrange 有限元方法的数值计算会面临网格畸变、计算精度下降等问题[13]，即使引入合理的单元删除准则，也会带来系统能量不守恒、结构刚度降低等问题[14]；而SPH 方法属于无网格方法，避免了强冲击载荷下网格扭曲和单元失效，但是计算每个粒子的物理量比较费时，其计算效率远低于有限元法[15]，而且SPH 方法在固体力学的应用中存在边界拉伸不稳定等问题[16]。即便有学者提出采用SPH-Lagrange 耦合的方法来提高计算效率和避免边界拉伸的不稳定性，但是这种方式导致系统总能量严重损耗[17]。

在上述研究的基础之上，依据Li 等[18]的侵彻实验，利用有限元分析软件LS-DYNA，选取合适的网格尺寸和模型参数，建立弹体和花岗岩靶体的计算模型，采用Lagrange 算法、SPH-Lagrange 耦合算法以及SPH 算法分别进行数值模拟，基于计算效率、侵彻深度、速度衰减、靶体损伤、Mises 应力分布等方面，对比分析3 种算法在弹体侵彻、贯穿岩石靶体数值模拟中的优势及不足。

1 模型与算法

1.1 计算模型

本研究采用Lagrange、SPH-Lagrange 及SPH 算法分别模拟弹体侵彻花岗岩的全过程，采用文献[5]中的弹体侵深及靶体损伤，验证数值模拟的有效性，实验数据见表1。实验中，采用二级轻气炮，使子弹以1 200～1 600 m/s 的速度正侵彻靶体，子弹和靶体试样见图1[5,18]。其中，子弹直径10.8 mm，长54.0 mm，弹头形状系数CRH（Caliber-radius-head）值为3.0，弹体材料采用30CrMnSiNi2A 高强度合金，密度7 850 kg/m3，初始质量32.45 g，杨氏模量211 GPa；花岗岩靶体试样长300 mm，宽300 mm，高800 mm，四周用外径480 mm、厚10 mm 的钢桶包裹，并用10 mm 厚钢板封底，在钢桶和试样之间用混凝土填充，确保对试样的约束，整体可视为半无限靶体。靶体材料选取山东省五莲县花岗岩，密度2 670 kg/m3，单轴抗压强度约150 MPa，杨氏模量54.6 GPa，泊松比0.3，纵波速度4 200 m/s。

表1 侵彻实验数据Table 1 Test results of projectile penetration

图1 实验试件Fig. 1 Experiment sample

数值模拟中，考虑弹体和目标靶体的轴对称性，在对称面设置对称边界，建立1/4 模型，以提高计算效率，并在靶体模型外围设置无反射边界，模拟半无限靶体。为研究弹体贯穿靶体的情况，将靶体模型高度由800 mm 设置为100 mm（实验中子弹速度为1 196 m/s 时的侵深为118.80 mm）。为更好区分两类有限元模型，如图2 所示，用于模拟实验的数值模型称为800 mm 模型，用于研究弹体贯穿靶体的数值模型称为100 mm 模型。

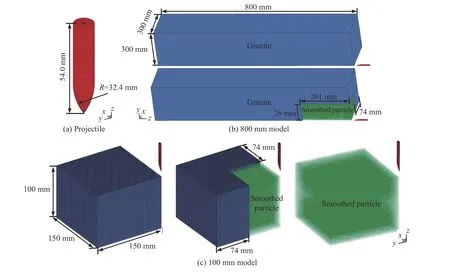
图2 计算模型Fig. 2 Model of projectile and granite target

初始时刻建立Lagrange 有限元模型，模型网络划分采用Solid 164 八节点六面体单元，利用侵蚀面面接触算法模拟弹靶接触，并添加单元删除准则。然后利用LS-PrePost 将单元转化为SPH 粒子，用侵蚀点面接触代替侵蚀面面接触，不再使用单元删除准则。如图2 所示，800 mm 模型中，由于单元数众多，将其全部转化为SPH 粒子后计算困难，所以只将弹靶作用近区内的单元转化为SPH 粒子，建立SPH-Lagrange耦合模型，SPH 粒子与Lagrange 网格之间设置点面绑定接触；100 mm 模型中，单元转化为SPH 粒子，分为两种形式，一是建立SPH-Lagrange 耦合模型，二是将靶体单元全部转化为SPH 粒子，建立SPH 模型。

1.2 模型选择

本研究中，子弹采用LS-DYNA 数据库中*MAT_PLASTIC_ KINEMATIC 模型，该模型属于考虑应变率效应的双线性模型，模型屈服后会沿线性硬化，可描述各向同性硬化和随动硬化塑性，能够很好地模拟金属等弹塑性材料的力学响应[19]。详细参数[20]见表2，其中 ρp为质量密度，VP 表示考虑应变率效应的计算方法。当VP = 0 时，通过缩放屈服应力进行计算；当VP = 1时，调用黏塑性公式执行计算。

表2 子弹材料参数Table 2 Properties of test projectile

模型本构方程为

根据 β值的不同，可以用来描述不同的硬化模型，如图3(a)所示： β=0 时，随动硬化，屈服面大小不变，沿塑性应变方向移动； β=1 时，各向同性硬化，屈服面位置不变，大小随应变而变化； 0 ＜β ＜1 时，混合硬化。

图3 模型描述Fig. 3 Model description

花岗岩靶体选用LS-DYNA 数据库中的*MAT_RHT 模型。该模型由德国Ernst-Mach 研究所（EMI）的 Riedel、Thoma 和Hiermaier 于1998 年首次提出[19]，经过近20 年的发展，被广泛应用于爆炸冲击等领域的数值模拟中，能够较好地描述混凝土、岩石等脆性材料受侵彻爆炸作用时的动态力学行为。RHT 模型充分考虑了弹性极限面、失效面以及损伤软化段残余强度，用于研究混凝土在动载作用下的初始屈服强度、失效强度和残余强度的变化[21]，还可以较准确地描述混凝土、岩石等脆性材料应力-应变曲线弹性、线性强化以及损伤软化3 个阶段，如图3(b)所示，其中， σ¯ 、 ε¯表示等效应力、等效应变，σfail、σelastic和σresidual分别为失效应力、弹性极限应力和残余应力。同时，RHT 模型采用了Herrmann 提出的p-α状态方程，用于描述在高速冲击等问题中当材料处于流动状态时静水压力、材料密度和内能之间的关系[22]。

对于材料压密后的状态方程，用多项式函数表示

在测得花岗岩基本物理力学参数的基础上，通过理论计算和参数研究[23]确定用于模拟花岗岩的RHT 模型参数，具体参数见表3。

表3 RHT 模型参数Table 3 Parameters of RHT material model

1.3 SPH 算法

SPH 算法是一种流体力学模拟的无网格光滑粒子算法，以插值理论为基础，通过任意分布的光滑粒子来计算各种边界条件下的物理力学方程。在算法中，并不是单独的计算粒子，而是通过核函数来逼近区域内任意粒子周围的场变量。考虑材料的弹塑性效应时，核函数W和插值公式可分别表示为[13]

2 数值验证

2.1 网格收敛性分析

选择合适的网格尺寸是精确模拟的关键，为确定本研究中花岗岩模型的网格大小，首先建立正方形网格，并采用无量纲比例参数 λ，其定义为弹体半径与网格长度之比。如表4 所示，当 λ为 1、2、3、4、5、6 时，构造相应的数值模型，并进行弹体侵彻深度计算。在数值模拟中，子弹选用*MAT_PLASTIC_KINEMATIC 模型，弹体材料的屈服强度高，侵彻结束后，弹体只发生轻微形变，弹径未发生变化，可以将其视为具有刚性性能的高屈服强度弹体，因此，在固定弹径条件下进行靶体网格收敛性分析时，子弹采用该双线性模型是合理可行的。图4 展示了弹体速度为1 196 m/s 时，不同比例参数 λ对应的侵彻深度-时间曲线。随着λ 的增加，即随着网格尺寸变小，侵彻深度逐渐趋于收敛， λ为 4、5、6 时，侵彻深度基本一致，且与实验结果较接近，满足精度要求。因此，为减少计算资源占用，提高计算效率，后续仿真模型采用 λ = 4 的比例参数，即网格尺寸为1.35 mm。

图4 不同网格尺寸下侵深-时间关系曲线Fig. 4 Time history of penetration depth with different mesh sizes

表4 网格尺寸与侵彻深度Table 4 Mesh size and penetration depth

2.2 数值验证

选取表1 中的3 组实验（No.1、No.2 和No.4）进行数值模拟，子弹选用*MAT_PLASTIC_KINEMATIC 模型，花岗岩靶体选用*MAT_RHT 模型，网格比例参数取 λ = 4，模拟获得的侵深-时间曲线如图5 所示。当子弹速度为1 196、1 400、1 630 m/s 时，对应的侵深分别为119.07、149.17、171.80 mm，与表1 中实验数据较为接近。然而随着侵彻速度不断增加，模拟中侵深与实验之间的差距逐渐变大，主要原因是随着侵彻速度增加，实验中子弹的磨损不断增大，而模拟中子弹形变不大，从而导致模拟中侵彻深度略高于实验。图6 显示了侵彻速度为1 400 m/s 时，模拟中靶体损伤情况及实验中靶体宏观破坏形态，其中数值模拟通过云图的形式显示靶体的破坏损伤情况，0 表示岩石未损伤，1 表示岩石已完全破坏。

图5 不同侵彻速度下侵深-时间关系曲线Fig. 5 Time history of penetration depth with different velocities

图6 侵彻速度为1 426 m/s 时靶体的损伤Fig. 6 Target damage at an impact velocity of 1 426 m/s

通过实验与数值计算的结果对比，数值计算获得的侵彻深度及靶体损伤与实验结果吻合度高，模拟重现了花岗岩靶体在弹体高速侵彻下的损伤与破坏，因此建立的计算模型适用于弹体高速侵彻花岗岩靶体的相关研究，尤其是在预测弹体侵深和靶体损伤方面。

3 数值计算及结果分析

基于已验证的本构模型和网格比例参数 λ，在子弹初速度为1 196 m/s 的条件下，分别对800 mm 模型和100 mm 模型进行数值计算。其中，800 mm 模型分为两类：一是有限元模型，命名FEM-1（Finite element model-1），单元数3 647 448；二是耦合模型，命名SPH-FEM-1（Smooth particle hydrodynamics-finite element model-1），单元数3 341 923，SPH 粒子数305 525。100 mm 模型分为3 类：一是有限元模型，下称FEM-2，单元数690 408；二是耦合模型，下称SPH-FEM-2，单元数521 008，SPH 粒子数169 400；三是SPH 模型，下称SPH-2，SPH 粒子数690 408。

3.1 800 mm 模型

图7 给出了采用Lagrange 算法和SPH-Lagrange 耦合算法数值模拟得到的侵彻路径和靶体损伤的对比。如图7 所示，Lagrange 算法导致弹体侵彻路径周边的单元发生畸变，耦合算法则无单元畸变，能够很好地模拟子弹击打靶体时粒子溅射飞散的过程，这是因为弹体高速侵彻时Lagrange 网格产生大变形而SPH 粒子可以任意流动。同时，与Lagrange 算法相比，耦合算法中侵彻会形成较大前坑区，而且侵彻路径周边严重损伤区域（0.8～1.0）直径更大，与实验结果吻合度更高，这是由于Lagrange 算法中需要添加删除准则，弹体打击产生的应力波在向四周传递过程中由于单元删除导致更多能量损耗，因此前坑区和严重损伤区域比较窄。但是，耦合算法中，由于应力波在不同算法模型中传播速度不同以及点面绑定接触算法在接触力传递方面有一定缺陷，导致在SPH 粒子和Lagrange 网格接触面的两侧，损伤变化非线性，存在明显的损伤差异。

图7 靶体损伤云图Fig. 7 Target damage of 800 mm model

如图8 所示，在SPH 粒子与单元接触面左右13.5 mm 的范围内，获取靶体自由面和对称面交界面上单元或SPH 粒子的PPV（Peak particle velocity），编号1～20。从图8 中看出，相较于Lagrange 算法，耦合算法中粒子区域的PPV 较低，而且在粒子与单元接触面的PPV 骤增，这与弹体和SPH 粒子及粒子和单元之间的点面接触有关。但是，在有限单元区域，两种算法中的PPV 逐渐趋于一致。由此，基于PPV 准则[24]，应用耦合算法研究花岗岩靶体的侵彻损伤时，要注意中心区域的应力及损伤可能会低于预期，粒子和单元的过渡区域损伤会高于预期，而一定范围外花岗岩靶体的损伤和稳定性可以基于PPV 准则进行较准确的评估。

图8 质点峰值振动速度Fig. 8 PPV of target points

图9 展示了两种算法得到的靶体的Mises 应力分布情况。图10 为两种算法得到的侵彻速度-时间关系曲线。由图9 可以看出，与Lagrange 算法中靶体Mises 应力环形分布相比，耦合算法中，中间正方形区域为SPH 粒子，在粒子与单元接触表面的4 个角出现应力滞后，接触面比尖角处应力大，主要是由粒子与单元之间的接触算法导致的。由图10 可以看出，Lagrange 算法中侵深为119.07 mm，耦合算法中侵深为114.79 mm，均与实验结果118.80 mm接近，考虑到数值模拟中弹体无磨损，因此Lagrange算法更符合实际情况。但是，从侵彻速度-时间关系曲线中发现，与耦合算法相比，Lagrange 算法得到的速度衰减不平滑，这是由算法中添加的删除准则造成的。同时，两种算法中侵彻速度衰减至零后均出现速度反向增加的情况，主要原因是弹体采用*MAT_PLASTIC_ KINEMATIC 模型描述，侵彻过程中产生形变，储存部分变形能，在侵彻结束后，能量释放，导致弹体出现反弹。

图9 0.04 ms 时Mises 应力分布Fig. 9 Von Mises stress at 0.04 ms

图10 侵深-时间和速度-时间关系曲线Fig. 10 Time history of penetration depth and velocity

计算效率方面，设置同样的计算总时间和时间步长，应用Lagrange 算法数值模拟需要3.0 h，耦合算法需要17.1 h。综合考虑靶体损伤、弹体速度和侵深、Mises 应力分布以及计算时间等方面，800 mm 模型的计算中，如果只考虑侵彻路径近区的靶体损伤和粒子飞溅效果，耦合算法更合适；如果考虑计算效率、侵彻深度、应力波传播等，推荐Lagrange 算法。

3.2 100 mm 模型

图11 为Lagrange 算法、SPH-Lagrange 耦合算法和SPH 算法数值模拟得到的侵彻路径和靶体损伤的对比。由图11 可知，Lagrange 算法导致弹体侵彻路径周边的单元发生畸变，其他两种算法则无单元畸变，能够很好地模拟子弹击打靶体时粒子溅射飞散过程，这得益于SPH 粒子的任意流动性。在耦合算法和SPH 算法中，侵彻会形成较大的前坑区和后坑区，而且侵彻路径周边严重损伤（0.8～1.0）范围更广，与弹体侵彻贯穿靶体的工况相吻合；同时Lagrange 算法只有较小的前坑区，不存在后坑区，这主要与添加的删除准则有关。在耦合算法中，由于应力波在不同算法模型中传播速度不同以及点面绑定接触算法在接触力传递方面有一定缺陷，导致在SPH 粒子和Lagrange 网格接触面的两侧，损伤变化非线形，存在明显的损伤差异，而其他两种算法则不存在这种差异。

图11 靶体损伤云图Fig. 11 Target damage of 100 mm model

图12 给出了3 种算法中靶体的Mises 应力分布情况。图13 给出了3 种算法中弹体侵彻速度-时间关系曲线。由图12 可知，在耦合算法中，中间正方形区域为SPH 粒子，在粒子与单元接触表面的4 个角会出现应力滞后，接触面比尖角处应力大，而在其他两种算法中靶体的Mises 应力与实际情况一致，呈环形分布，这种应力分布的差异主要是由粒子与单元之间的接触算法造成的。由图13 可以看出，在耦合算法和SPH 算法中，两种弹体侵彻速度-时间曲线平滑且剩余速度一致。但是在Lagrange 算法中，由于添加的单元删除准则，导致侵彻速度衰减存在波动且剩余速度较大。

图12 0.04 ms 时Mises 应力分布Fig. 12 Von Mises stress at 0.04 ms

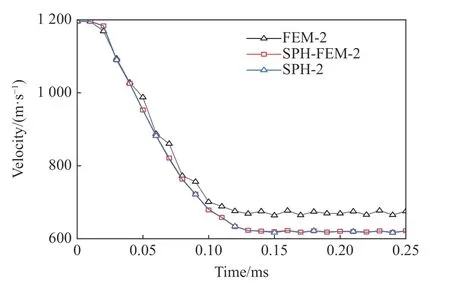
图13 采用不同算法得到的侵彻速度-时间关系曲线Fig. 13 Time history of velocity with different algorithm

计算效率方面，设置同样的计算总时间和时间步长，采用Lagrange 算法进行数值模拟需要0.65 h，耦合算法需要3.60 h，SPH 算法需要8.30 h。综合考虑靶体损伤、弹体速度和侵深、Mises 应力分布以及计算时间等方面，100 mm 模型的数值模拟中，如果只考虑弹体侵彻贯穿靶体形成的前/后坑区、粒子飞溅效果以及子弹的剩余速度，耦合算法更合适；如果只考虑时间效率，则推荐Lagrange 算法；如果考虑数值模拟的准确性、应力波传播等，则SPH 算法更优。

4 结 论

基于Lagrange 及 SPH 算法，对弹体高速侵彻岩石靶体进行了数值模拟，对比分析了Lagrange算法、SPH-Lagrange 耦合算法以及SPH 算法的优劣性。

（1）在弹体侵彻岩石靶体的数值模拟中，Lagrange 算法的计算效率高，计算结果较准确，通过设置无反射边界可以模拟弹体侵彻半无限靶体，但是存在无法展示靶体溅射、前坑区小、无后坑区等问题，利用RHT 模型显示的损伤云图，则可以获取较准确的前坑区和后坑区范围，进而间接解决Lagrange 算法存在前坑区小、无后坑区的问题。

（2）SPH 算法可以清晰显示侵彻时靶体粒子的飞散，计算结果较准确，但是计算效率低，粒子过多时还可能造成计算停止。

（3）SPH-Lagrange 耦合算法兼具SPH 和Lagrange 算法的优势，但是由于粒子与单元之间接触的问题，会产生应力滞后和应力波不稳定传播的现象。在应用耦合算法研究侵彻爆炸问题时，关于侵彻爆炸中心区域的岩体破坏判定，需要考虑应力滞后、应力波不稳定传播等的影响。关于一定范围外地下结构的稳定性评估，可基于PPV 准则进行较准确的研究。

（4）在单元数较少的小模型中，采用SPH 算法可以更准确地研究侵彻问题。在单元数较多的大模型中，Lagrange 算法是比较合理的选择，耦合算法则需要进一步研究。