基于风光数据驱动不确定集合的配电网与多微网鲁棒经济调度
2021-10-20张宇威肖金星杨军徐冰雁李蕊李勇汇
张宇威,肖金星,杨军,徐冰雁,李蕊,李勇汇
(1.武汉大学电气与自动化学院,武汉市 430072;2.国网上海市电力公司,上海市 200122)
0 引 言
近年来,随着能源供需矛盾、气候变化和环境问题日益加剧,发展可再生能源成为未来能源系统的主要要求之一[1]。微网(microgrid,MG)作为集成各类分布式发电系统的有效形式,解决了大规模可再生能源的集成应用问题。多微网(multiple microgrids,MMGs)针对区域内邻近的分布式发电机组、MG和负荷的能量管理进行协调,不但可以降低MG对配电网(distribution network,DN)运行安全性的不利影响,而且可以提高可再生能源的消纳率[2]。由于DN与MMGs是包含多个利益主体以及多种不同类型分布式机组的耦合系统[3],如何在考虑可再生能源不确定性的前提下,兼顾各方利益,实现配电网与多微网系统可靠、经济运行调度是目前亟需解决的重要问题。
随着以风电、光伏为代表的可再生能源接入量的不断增加,其不确定性会给配电网与多微网系统运行的可靠性、经济性带来较大的挑战[4]。目前针对配电网与多微网系统中可再生能源不确定性的处理方法主要包括随机优化模型[5-6]、机会约束优化模型[7-8]、鲁棒优化模型[9-14]等。文献[5]采用随机优化,以拉丁超立方采样来产生随机场景,并采用同步回代削减法来缩减场景。文献[8]采用机会约束优化来描述可再生能源的不确定性问题,将旋转备用约束以概率形式描述。然而,随机优化方法需要实际工程中难以获得的随机因素的概率分布或者较多的数据样本,且计算速率和结果受场景数量的影响;机会约束方法由于其复杂的概率密度函数,其非凸约束难以同时保证求解效率和全局最优性。此外,这2种方法均难以保证调度的完全鲁棒性。
随着国家碳中和、碳达峰的发展趋势,配电网与多微网中风、光等可再生能源、电动汽车等渗透率越来越高,电网的运行方式越来越复杂多变,使得电网出现极限运行场景的风险急剧增加[10]。鲁棒优化作为一种处理不确定性的方法,由于考虑了不确定性集合中的最坏情况,相较于其他方法具有较高的鲁棒性,在配电网与多微网系统调度中能够有效应对极限运行场景。文献[11]研究了不确定性条件下考虑多利益相关者的多微电网能量调度问题,并建立了微网鲁棒调度模型。文献[12-14]考虑多种主体以及可再生能源不确定性,通过分布式鲁棒优化方法来解决配电网与多微网系统的分布式调度问题。
上述文献均采用基于区间集合的鲁棒优化方法处理可再生能源的不确定性,存在以下不足:1)忽略了可再生能源出力的时空相关性。考虑到微网中风电和光伏等可再生能源地理位置接近,在各时段都具有较强的相关性[15],因此忽略可再生能源的相关性会导致调度决策中考虑了实际发生概率非常低的出力场景,使得调度决策过于保守,从而导致调度经济性较差。2)上述基于区间集合的鲁棒优化模型,在求解时需要通过拉格朗日对偶原理将子问题进行转化,使得求解过程较为复杂,经济性也不理想。
本文提出一种考虑风光出力时空相关性的配电网与多微网数据驱动鲁棒调度方法。通过分布式调度算法,分别建立配电网与微网的调度模型;针对微电网中风光出力的不确定性与时空相关性,采用最小体积封闭椭球(minimum volume enclosing ellipsoid,MVEE)数据驱动算法构建风光出力不确定集合,建立微网数据驱动鲁棒调度模型;采用基于极限场景的列约束生成(column-and-constraint generation,C&CG)算法将微电网鲁棒调度问题拆分成主子问题进行求解,子问题不需要采用对偶方法,只需求解各个极限场景下的微电网实时调度问题;采用目标级联分析法(analytical target cascading,ATC)对配电网与多微网调度问题进行整体求解。仿真结果表明所提方法能够在保证配电网与多微网调度鲁棒性的同时,提高系统调度的经济性。
1 配电网与多微网分布式调度框架
本文研究的配电网与多微网系统模型如图1所示。配电网通过变压器从上游主网购电,微网侧通过风光机组以及可控机组发电,两网之间通过联络线进行电能双向交互,以实现配电网与多微网经济调度最优。针对配电网与多微网的整体建模,目前已有相关研究[16-17]采用分布式建模方法将配电网与微网进行分别建模,从而提高计算效率。对此,本文提出一种配电网与多微网分布式优化调度框架,将配电网与多微网作为多个利益主体,分别建立调度模型,在各系统进行调度决策时仅通过彼此内部的部分信息交互,分布式实现各自的最优调度。配电网与多微网的调度框架为:
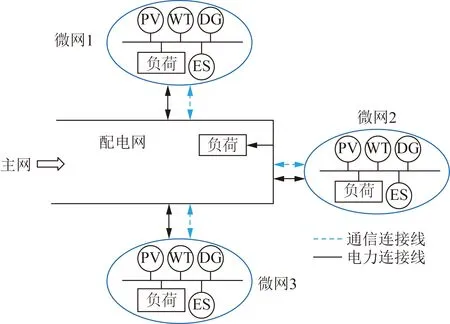
图1 配电网与多微网结构Fig.1 Structure of DN and MMGs
(1)
式中:fDN、fMG分别为配电网与微网的经济调度目标函数;xDN为配电网自身的调度决策变量,包括向主网购电功率、线路电流等;xCO为配电网与微网的耦合调度变量,指配电网与微网交互功率;xMG为微网自身调度变量,包括机组出力计划、储能充放电计划等;D(·)、E(·)分别为配电网调度的不等式约束和等式约束;G(·)、H(·)分别为微网调度的不等式约束和等式约束。
该优化问题为一个双层优化问题,包括配电网层以及微网层,层之间通过耦合变量进行联系。本文首先建立配电网和微网调度模型,再采用ATC算法对整体模型进行求解。
1.1 配电网调度模型
配电网调度以满足自身负荷需求为前提,确定日前最优主网购电方案以及与微电网交互功率,其目标函数为总运行成本最小。
1.1.1配电网调度目标函数
(2)
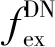
1.1.2约束条件
(3)
(4)
(5)
(6)
(7)
(8)
(9)
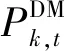
在配电网约束中,式(3)—(6)为配电网潮流约束,式(7)、(8)为线路电流、节点电压上下限约束。式(5)为非凸约束,可将其转为二阶锥约束:
(10)
1.2 微网日前-实时二阶段鲁棒调度模型
1.2.1微网调度目标函数
针对微网内风光可再生能源的不确定性,本文提出一种微网两阶段鲁棒调度模型,调度包括日前和实时2个阶段,日前阶段基于风光出力场景制定日前调度方案,实时阶段考虑风光出力的不确定性,基于日前阶段方案进行实时调整,以实时调度成本最小为目标确定各单元的出力实时调整策略。微网调度模型目标函数为:
(11)
式中:Ω1、Ω2、Ω3分别为日前调度决策变量集合、风光出力不确定性变量集合和实时调度决策变量集合;COk表示微网k日前阶段的调度成本;CRk表示微网k实时调度成本。
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
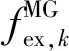
1.2.2日前调度约束
1)燃气轮机日前备用容量约束。
根据文献[18]可知,由于实时出力计划会带来不便,燃气轮机机组需要在日前制定预出力计划以及机组的上下备用容量。
(24)
(25)
2)燃气轮机最小启动/关闭时间约束。
(26)
(27)
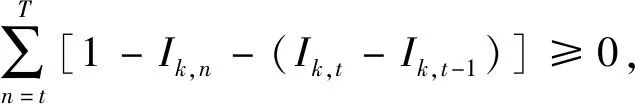
(28)
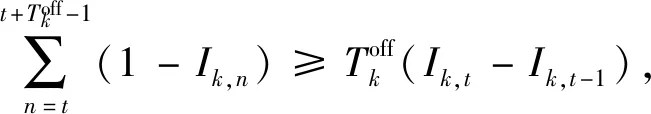
(29)
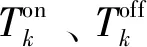
3)联络线功率传输约束。
(30)
1.2.3实时调度约束
1)燃气轮机出力爬坡约束。
(31)
式中:RUk、RDk分别为燃气轮机机组的最大爬坡和滑坡功率。
2)微电网功率平衡约束。
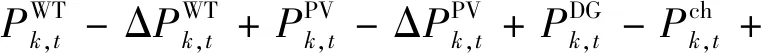
(32)
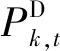
3)储能充放电容量约束。
(33)
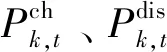
4)弃风、弃光以及失负荷约束。
在风电与光伏出力向上波动较大的极端场景中,若储能容量有限,则需要弃风弃光以维持功率平衡[10,19]。此外,本文在调度中考虑可中断负荷,在极端场景下可切除小部分可中断负荷[10,19]以满足功率平衡。
(34)
(35)
(36)
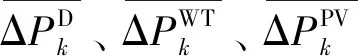
5)燃气轮机出力最大/最小值约束。
(37)
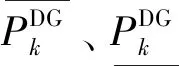
6)燃气轮机出力实时调控约束。
在实时调度中,考虑可再生能源出力的不确定性,燃气轮机的实时出力可能会偏离日前计划出力,其实时出力调整可由式(38)—(39)计算。
(38)
(39)
2 基于数据驱动鲁棒优化的不确定集合描述
1.2节中的微网二阶段鲁棒调度问题是考虑风光不确定集合Ω2中最恶劣场景的调度问题。不确定集合Ω2的构建会影响调度问题的鲁棒性和经济性。本节在1.2节的基础上构建风光数据驱动不确定集合,从而建立微网数据驱动鲁棒调度模型。
2.1 数据驱动不确定集构建
目前在针对微电网中可再生能源不确定性的鲁棒优化研究均采用区间不确定集合对不确定变量进行描述[11-14],然而区间不确定集合忽略了不确定变量之间的相关性;。风电以及光伏出力的区间不确定集合只由各自历史场景中的最大和最小出力决定,忽略了风光的相关性。若用区间集合对其进行描述,会过多考虑不可能发生的场景,为额外应对这些场景必然会增加调度成本。
与区间不确定集合相比,椭球更适用于模拟非均匀的数据集,其兼顾了每个变量的不同方差和变量间的协方差(即变量间的相关性)。一般椭球集合的表达式为E={(ω-c)Tθ-1(ω-c)≤1},其中c为椭球中心;θ为经加权的变量协方差,反映变量之间的相关性;ω为风-光历史出力矩阵。椭球不确定集合可以调整长短轴以及偏移角度适应不同相关性的数据[20]。
针对椭球不确定集合的构建,MVEE算法[21]根据不确定变量历史数据的分布情况,采用数据驱动方法构建一个能够包裹所有历史数据的最小体积椭球不确定集合,该集合能够描述风-光出力的时空相关性,其包围的不确定性出力空间更小,保守性也更小。图2为单时段风-光区间及椭球不确定集合对比。

图2 风光区间不确定集以及椭球不确定集Fig.2 The cubic set and the ellipsoid set
数据驱动不确定集合的构建方法如下[22]:
步骤1:根据历史数据构建风-光历史出力矩阵ω。假设区域内共有Nw个风电机组,Np个光伏电站,将所收集的风-光出力历史数据按天进行划分,设所收集到的历史数据的天数为Ns。ω的表达式可写为:
(40)
步骤2:基于数据驱动的高维椭球集合构建。基于MVEE数据驱动算法,构建一个高维的椭球来包裹所有的历史场景。
(41)
式中:ρ为常数,代表(Nw+Np)T维的单位球体的体积;Q为椭球的对称轴相对坐标轴的偏离方向。
式(41)可以采用lift-and-project算法进行求解[21]。最终得到高维椭球的表达式为:
E(Q,c)={ω∈R(Nw+Np)T|(ω-c)TQ(ω-c)≤1}
(42)
式(42)所描述的(Nw+Np)T维椭球不确定集合共有2(Nw+Np)T个顶点。
步骤3:求解模型,得到椭球集合的顶点坐标。首先,对Q进行正交化分解:Q=PTDP=P-1DP,记D=diag(λ1,λ2,…,λ(Nw+Np)T),P为变换矩阵。为得到高维椭球对应的顶点,将该椭球旋转平移,使其对称轴与坐标轴重合,该旋转变化方程为:
ω′=P×(ω-c)
(43)
E′(D)={ω′∈R(Nw+Np)T|ω′TQω′≤1}
(44)
(45)
式中:ω′为旋转后顶点的坐标值;E′(·)为旋转后得到的高维椭球表达式;ω′e,1,…,ω′e,Ne为旋转后的高维椭球顶点坐标;Ne为顶点的个数。
得到高维椭球E顶点ωe,i坐标,从而建立基于椭球顶点的数据驱动不确定集合[22]。
2.2 微网二阶段数据驱动鲁棒优化模型
综合1.2节微网二阶段调度模型以及2.1节所述的数据驱动集合,可以建立微网二阶段数据驱动鲁棒调度模型,其矩阵表示如式(46)所示。凸优化中极值必然存在于多面体空间的顶点处[23-24],所以数据驱动鲁棒优化的极限场景位于椭球顶点处。对于已确定的日前调度变量x∈Ω1,只要调整实时调度变量y∈Ω3能适应所有极限场景ωe,h,那么就可以保证调度的鲁棒性。
(46)
式中:h为极限场景编号;A、B为系数矩阵;G(·)、H(·)分别为微网调度的不等式约束和等式约束。
3 模型求解
3.1 微网数据驱动鲁棒调度模型求解
式(46)的微网二阶段鲁棒调度模型为三层优化问题,无法直接求解。传统的C&CG算法通过将原问题拆分成为主子问题迭代求解[18],主问题为求解多个极限场景下最优决策问题,子问题则是通过拉格朗日对偶求解max-min问题,然而对偶转换会使得求解过程较为复杂。
考虑数据驱动不确定集合的特性,本文提出一种基于极限场景的改进C&CG算法。改进C&CG算法主问题为求解多个极限场景下最优日前调度策略,子问题则是通过极限场景法来寻找在当前日前调度方案下的最恶劣场景,并通过添加最恶劣场景的实时调度约束条件到主问题,影响主问题决策。另外,由式(42)可知,当不确定变量为n时,基于椭球顶点的数据驱动不确定集合的极限场景数为2n,相对于极限场景数为2n的区间不确定集合能够有效降低求解负担,可以采用枚举极限场景的方法求解子问题。相对于常规的采用对偶原理的C&CG算法,该方法中每个极限场景下的子问题均为不包含整数变量的线性调度问题,可以并行求解,相对简单。
改进C&CG算法主问题的形式为:
(47)
式中:n为当前C&CG算法迭代次数;η表示主问题极限场景中微电网的最大实时调度成本;wh为第h次迭代时选取的极限场景;ywh为极限场景wh下实时调度决策变量;ωe,wh为极限场景wh下不确定变量取值。
改进C&CG算法子问题的形式为:
(48)
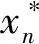
基于极限场景法的改进C&CG算法步骤如下:
步骤1:设定下界LB=-∞,上界UB=+∞,算法迭代次数n=1。
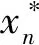
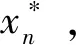
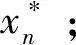
数据驱动鲁棒优化算法流程如图3所示。
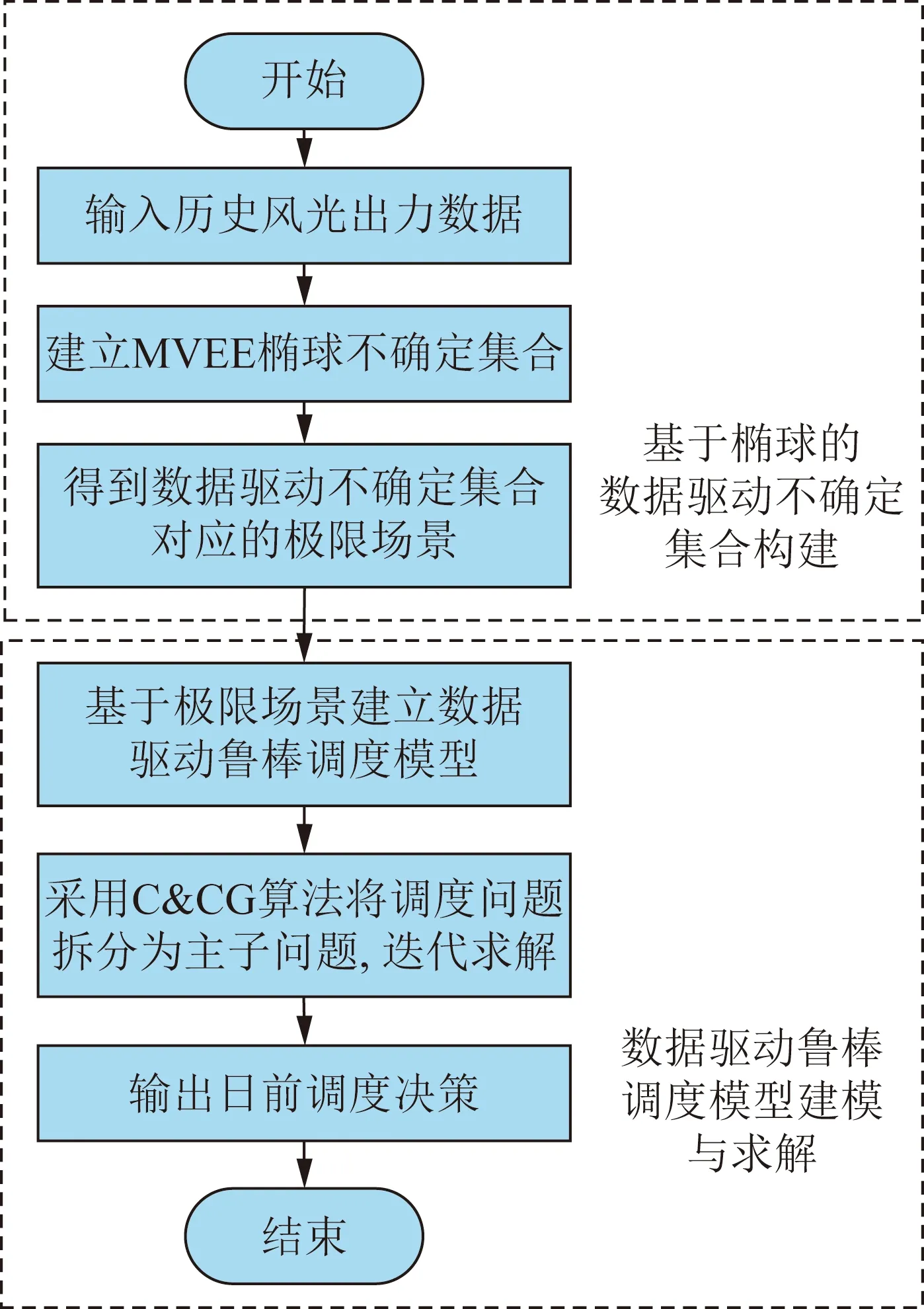
图3 数据驱动鲁棒优化算法流程Fig.3 Flow chart of the data-driven robust optimization method
3.2 配电网-多微网整体模型分布式求解
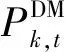
ATC方法求解配电网-多微网整体调度模型步骤如下:
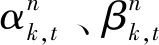
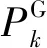
(49)
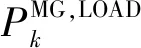
(50)
步骤4:对配电网和微电网的多次优化迭代,直至满足收敛判据[8]。
假设配电网与多微网系统中共有3个微网,则配电网与多微网系统整体求解流程如图4所示。
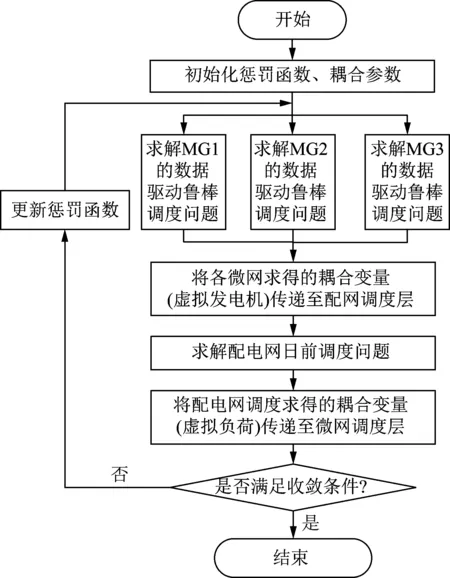
图4 基于ATC的配电网与多微网系统调度流程Fig.4 Flow chart of dispatch solving based on ATC
4 仿真分析
采用IEEE 33节点配电网以及3个微电网进行仿真验证,其拓扑如附图A1所示。其中MG1为居民型微网,MG2为商业型微网,MG3为工业型微网,均包含1台风机、1台光伏、1台微型燃气轮机以及1台储能设备,峰值负荷均为1.3 MW,这3类微网具有不同的负荷曲线,具体如附图A2所示[26]。MG1、MG2、MG3接入的风机与光伏容量均为500 kW。微电网通过联络线与配电网节点连接,联络线功率传输最大值为500 kW。配电网节点1通过变压器从主网购电,配电网的单位网损成本为0.6元/(kW·h)。微型燃气轮机机组的接入容量均为800 kW,出力成本系数参考文献[18]。削减负荷的惩罚成本为6元/(kW·h),弃风和弃光惩罚成本为0.6元/(kW·h)[26]。燃气轮机日前上下备用容量成本为0.3元/(kW·h),实时向上和向下再调度成本分别为0.3元/(kW·h)[20]。各微网的储能设备容量均为600 kW,最大充放电功率为200 kW,充放电效率为0.9。微电网与配电网购售电单价参考文献[27]。
考虑光伏只在白天出力[28],设置仿真时间为12 h。采用瑞士地区风电和光伏出力的历史数据作为仿真数据集[29]。
为验证所提方法的有效性,通过MATLAB软件进行建模,并利用Gurobi算法包进行计算。
4.1 优化结果分析
实际C&CG算法迭代所用的数据驱动不确定集合的极限场景如附图A3、A4所示,其中S1、S2、S3、S4为C&CG算法在4次迭代中选取的4个风光出力极限场景。作为对比,采用区间集合的传统鲁棒调度模型进行调度时,其C&CG算法迭代中选择的极限场景见附图A5、A6所示。可以看出,区间不确定集合的极限场景位于风光出力的极值点处,且存在较多可再生能源出力爬坡极大的极限场景,然而考虑到可再生能源出力的时空相关性,这种恶劣情况出现的概率较小。而数据驱动不确定集合的极限场景考虑了可再生能源出力的时空相关性,降低了不确定集合的保守性。
图5为配电网日前调度决策情况,其中微网虚拟负荷为正表示微网向配电网买电,反之则表示微网向配电网售电,可以看出,配电网向主网的购电功率曲线较为平稳。其中,居民型微网MG1和商业型微网MG2在09:00—17:00时段用电负荷较大,从配电网购电功率较大。而工业型微网在白天电价较高时段用电负荷较少,将多余的电能出售给配电网。
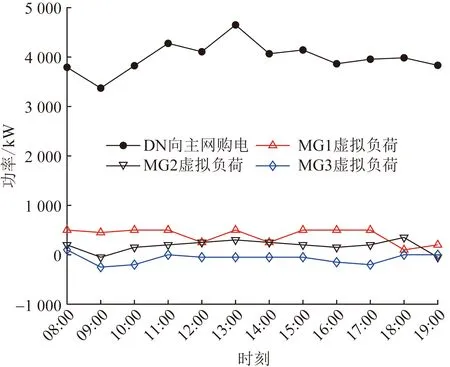
图5 配电网日前调度方案Fig.5 Day-ahead dispatching scheme of DN
图6为微网燃气轮机的日前预出力值以及日前向上和向下备用容量。整体来看,为满足微网负荷需求,所有微电网中的燃气轮机日前预出力较高,同时为防止发生大规模弃风、弃光情况,所有燃气轮机的向下备用容量要高于向上备用容量。从时段上看,燃气轮机在风光场景中出力都较大的13:00—15:00时段,为防止出现大规模弃风以及弃光现象,可控机组的向下备用容量显著高于其他时段。可以看出,多微网系统主要通过控制可控机组的日前备用容量来处理可再生能源不确定性。
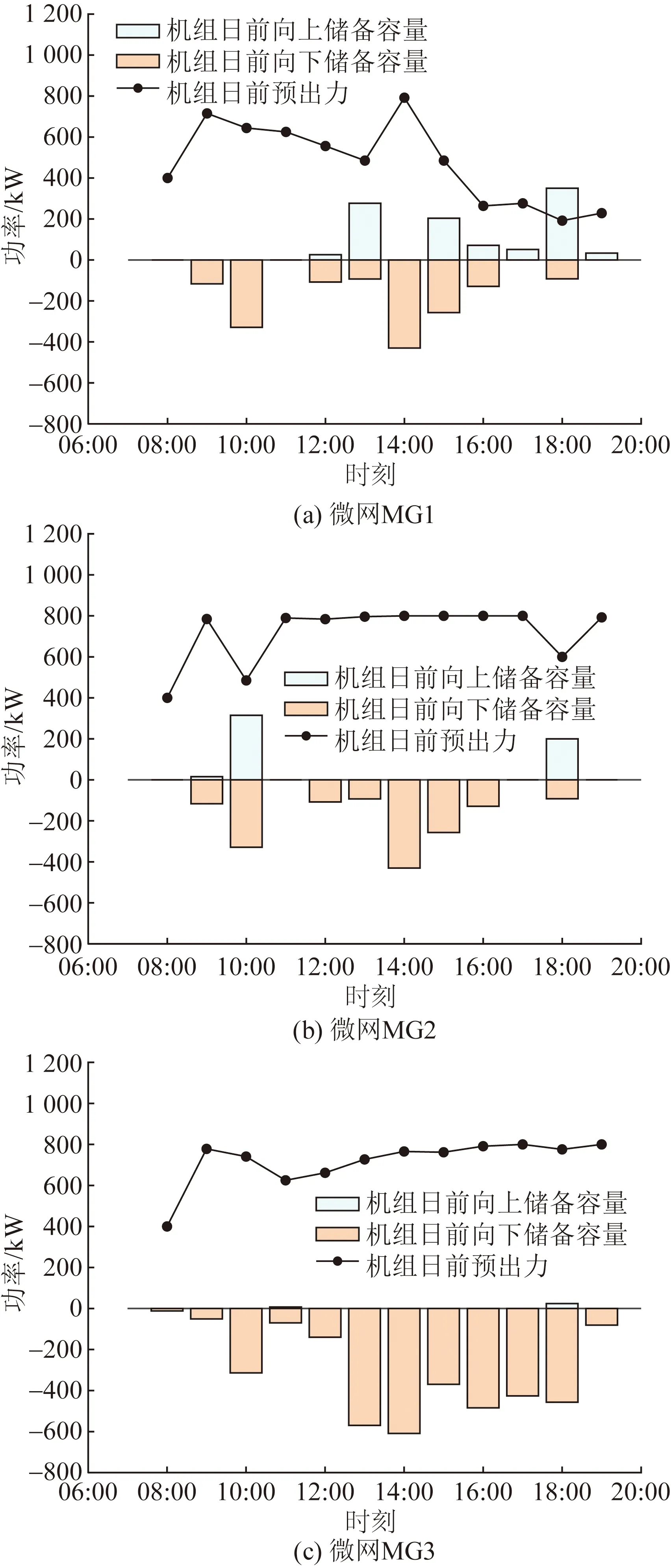
图6 各微网中燃气轮机机组日前预出力与备用容量Fig.6 Day-ahead scheduled output and reserve capacity of MT in MG
本文提出的ATC算法收敛曲线如图7所示,经过6次迭代实现快速收敛。此外,该算法基于历史数据进行建模,可以通过离线计算得到系统日前调度策略。在实时阶段求解系统每个实际场景下再调度的时间约为0.2 s(CPU i3 7100),可以满足系统运行调度的需求。
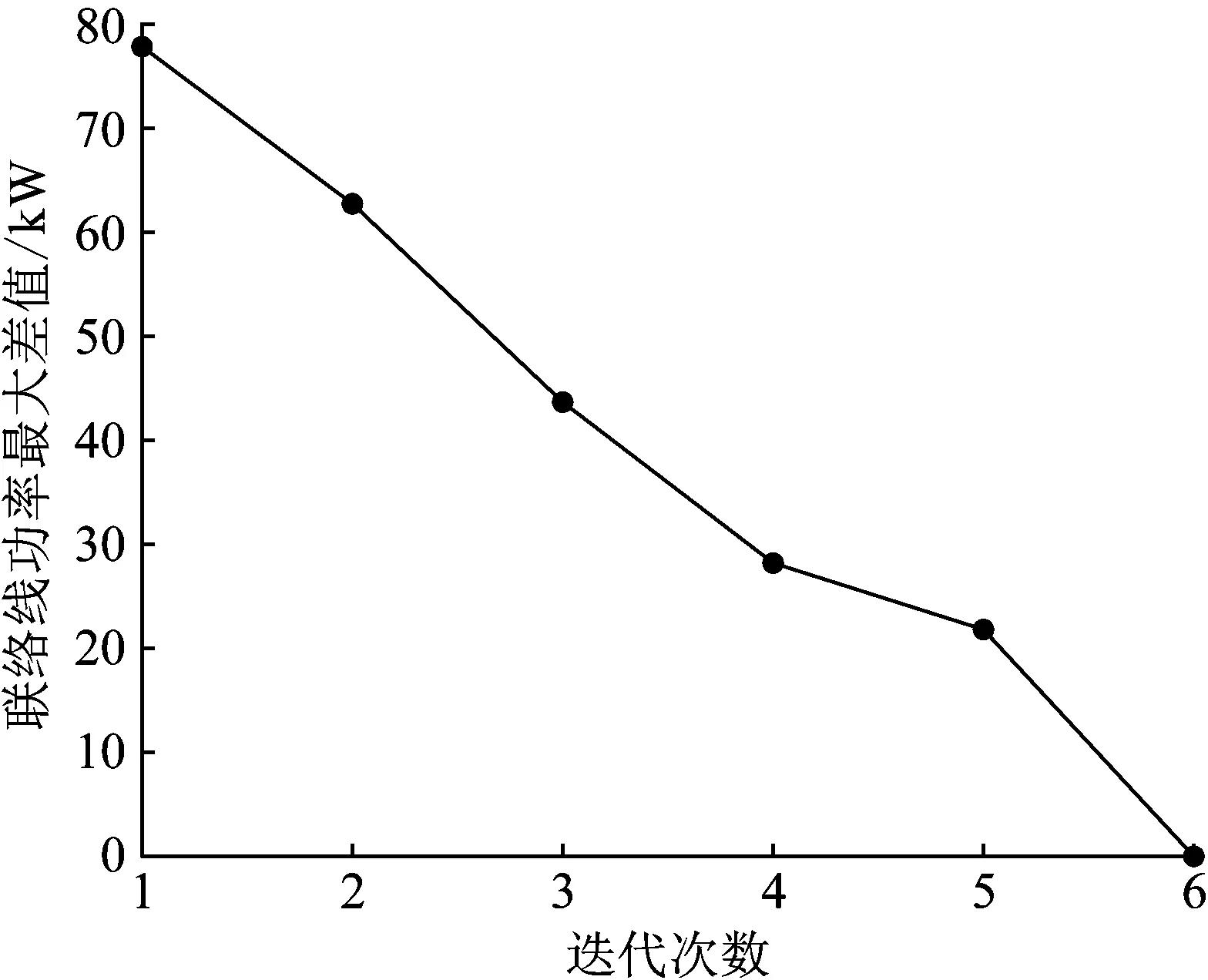
图7 ATC算法迭代收敛曲线Fig.7 The iterative convergence curve of ATC
4.2 鲁棒算法对比
为更好地说明本文所提考虑风光相关性的数据驱动鲁棒调度模型的有效性,将其与其他采用区间集合的鲁棒调度模型进行对比验证,具体如下:
场景1:采用本文所提鲁棒调度模型。
场景2:采用区间集合的传统鲁棒调度模型[30]。
场景3:采用区间集合的可调鲁棒优化调度模型[13]。
采用100组风光历史出力场景进行验证,不同算法的配电网、多微网调度成本对比如表1、2所示。其中平均成本和最大成本分别表示所有测试场景中该项成本的平均值和最大值。平均成本主要反映了调度的经济性指标,最大成本反映了调度的鲁棒性指标。多微网的平均成本和最大成本均为所有微网成本之和。
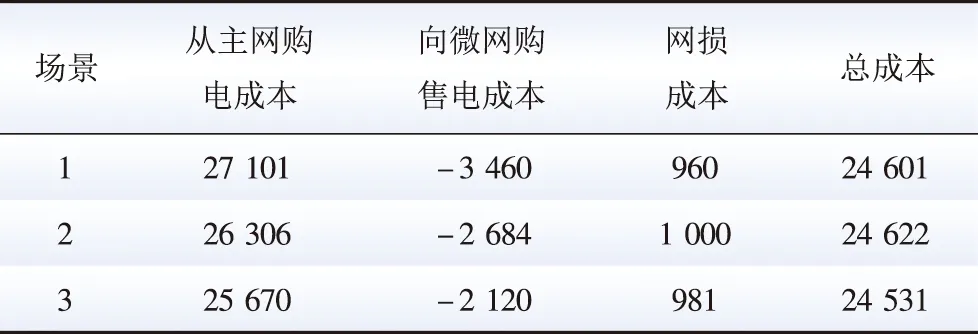
表1 不同优化算法下的配电网调度成本优化对比Table 1 Comparison of DN dispatch cost under different optimization methods 元
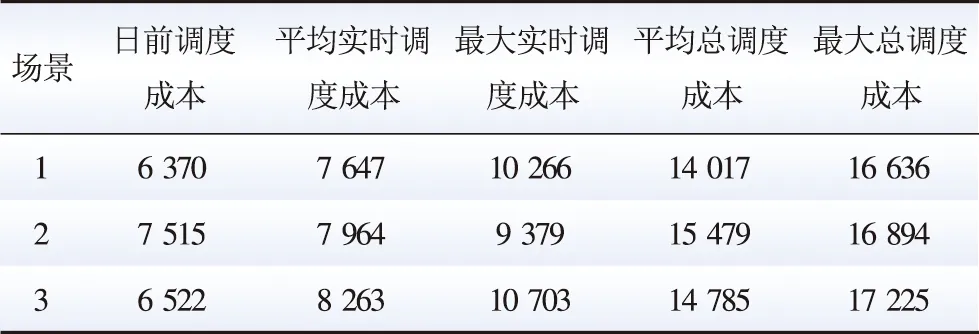
表2 不同优化算法下的多微网调度成本优化对比Table 2 Comparison of MMGs dispatch cost under different optimization methods 元
从对比结果可以看出:1)所有测试场景下配电网调度成本基本相同,可见可再生能源接入微网的情况下其出力不确定性对配电网调度的影响较小。2)从多微网最大总调度成本来看,本文算法的总调度成本最大值较传统鲁棒优化算法以及可调鲁棒调度算法的成本小,可以看出本文鲁棒性较强。3)从多微网平均总调度成本可以看出,本文所提方法的总调度成本平均值显著低于其他2种算法,可以提高配电网与多微网系统调度的经济性。
总体来说,本文所提的配电网与多微网数据驱动算法相比于采用区间集合的鲁棒调度方法,其优越性体现在能够在保证调度鲁棒性的同时,提高调度的经济性。
5 结 论
本文提出了一种考虑风光时空相关性的配电网与多微网数据驱动鲁棒调度算法。首先采用分布式调度算法分别建立配电网日前调度模型以及微电网日前-实时二阶段调度模型;考虑微网中风光不确定性以及相关性,通过数据驱动算法建立风-光数据驱动不确定集合,建立微网二阶段鲁棒调度模型,提出基于极限场景的C&CG算法进行求解。最后采用ATC算法进行配电网与多微网分布式求解。通过算例得到以下结论:
1)基于数据驱动方法捕捉风-光出力的时空相关性,建立了风-光数据驱动不确定集合。该集合相对于区间不确定集合降低了保守性。
2)提出了一种考虑风-光相关性的配电网与多微网系统数据驱动鲁棒调度方法,从而得到配电网与多微网的最优日前调度决策。算例结果表明所提的调度模型可以在保证系统调度鲁棒性的前提下,进一步提高日前调度和实时调度的经济性。
3)本文所提的配电网与多微网系统数据驱动鲁棒调度方法能够实现有效收敛,从而满足系统运行调度的需求。
