基于深度置信网络状态最优反馈的智能发电控制策略

戚焕兴,殷林飞,万俊,黄阳龙

(1.广西电网北海供电局,广西壮族自治区北海市536000；2.广西大学电气工程学院，南宁市530004)

0 引 言

在控制工程中，状态反馈量与控制性能的矛盾始终存在。一方面，系统中更多的状态反馈信息参与反馈控制将增加控制环与被控系统的耦合性，从而达到更优的控制性能。系统全状态信息协同反馈是实现最优控制的前提[1]。另一方面，实际系统中，全状态信息的测取通常是困难的，测取的状态量越多，由于各种因素导致的误差也会越大，个别状态信息甚至无法测取，因此全状态最优反馈(full state optimal feedback,FSOF)控制[2]在实际工程中存在较大局限[3]。这一矛盾在互联电力系统自动发电控制(automatic generation control,AGC)问题中尤其凸显。由于二次设备测量误差等原因[4]，各区域电网实时获取其他区域电网的准确状态信息较为困难，并且由于区域跨度大，状态信号的传输时延较大[5]，增加了信号的不确定性。因此，长期以来，全状态最优反馈控制在AGC应用中一直受到限制[6]。相反的，基于输出反馈的AGC策略，如比例-积分 (proportional integral,PI)控制[7]、次优(sub-optimal,SO)控制[8]等算法，虽然控制耦合性和控制性能欠佳，但因为易于实现，在我国得到推广使用并成为主流[9]。

然而，近年来，电力系统逐渐复杂化、多样化，为自动发电控制带来了新的难题。一方面，新能源机组装机容量逐年增加，发电能源逐渐环境友好化，风力发电[10]、光伏发电[11]等电站的出力具有较大的不稳定性，调频能力较差[12]，出力的随机变化常被纳入负荷扰动范畴,发电侧出力的整体随机性增加；另一方面，家庭分布式发电入网增加[13]、电动汽车逐渐兴起[14]一定程度上增加了负荷的随机性，负荷侧甚至可能出现功率倒送的情况，配电网模型面临重构[15]。电力系统负荷-频率控制(load-frequency control,LFC)模型日趋复杂化，传统AGC策略逐渐无法满足电力系统频率稳定性的要求。

近年来，一些新的控制算法逐渐被引入自动发电控制领域，如模糊控制[16]、强化学习控制[17]以及自适应控制[18]等，这些算法的引入在相当程度上改善了自动发电控制的性能，但其控制过程均缺少对整个系统全状态信息的协同考虑，无法在性能指标上达到最优控制，存在一定的局限性。

针对上述问题，本文结合深度置信网络(deep belief network,DBN)与最优控制理论，提出深度置信网络状态最优反馈 (deep belief network state optimal feedback,DBNSOF)算法，引入DBN对全状态最优反馈AGC系统进行学习，依靠DBN强大的非线性表达能力，辨识部分状态信息与最优控制值之间的高阶函数关系，最终，DBN根据所输入的系统部分状态量，计算并输出近似最优发电调控值。该算法可实现非全状态信息反馈下的系统近似最优发电控制。

本文所提出的DBNSOF算法，一方面，减少了AGC状态反馈量，降低对电气测量及通信设备的要求，在实际系统中更易实现；另一方面，DBN的非线性表达能力提高了反馈状态量与被控系统间的耦合程度，提升了AGC性能，将更好地匹配与满足智能电网背景下的运行需求[19]。

1 全状态最优反馈控制

在DBNSOF算法中，DBN的模型训练是基于数据实现的。因此，首先要实现基于全状态最优反馈的控制系统，以便于数据获取。本节对互联电力系统LFC模型的全状态最优反馈控制的实现进行介绍。

1.1 IEEE标准两区域互联系统的LFC频域模型

首先，建立互联电力系统的初始LFC模型，系统LFC频域模型图如图1所示，表1给出了系统参数。

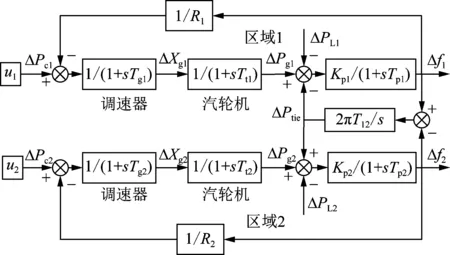
图1 两区域互联电力系统负荷-频率控制模型Fig.1 LFC model of two-area interconnected power system

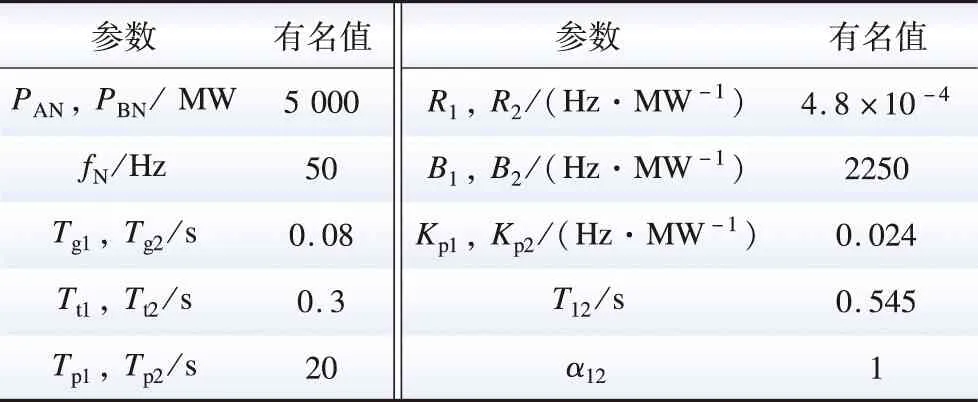
表1 两区域互联电力系统参数值Table 1 Parameter values of two-area interconnected power system

如图1所示的互联电力系统中，区域调度中心AGC将输出机组功率调控命令ΔPc1和ΔPc2(即二次调频命令)，伴随惯性时间Tg，该命令传递到调速器从而得到调节汽门的开度变化量ΔXg1与ΔXg2，再经Tt延时传递至汽轮机从而得到调控发电机组机端出力变化量ΔPg1与ΔPg2，与区域外传输功率偏差量ΔPtie、负荷扰动量ΔPL进行加减运算后得到区域功率—负荷偏差量，经延时比例响应后，输出区域频率偏差量Δf1与Δf2。而1/R1与1/R2分别作为Δf1与Δf2的负反馈增益，构成一次调频环。

如表1所示，系统参数中，PAN与PBN为区域基准功率容量；fN为额定频率；Tg1与Tg2为调速器惯性时间常数；Tt1与Tt2为汽轮时间常数；R1与R2为一次调频的调差系数；B1与B2为频率偏差响应系数；Kp1与Kp2为负荷-频率调节效应系数；Tp1与Tp2为其惯性时间常数；T12为联络线同步系数；α12为区域传输权重系数。

1.2 IEEE标准两区域互联系统状态空间模型

为求取上述系统的全状态最优反馈控制解，需将频域模型转化为时域模型，系统的状态空间表达式如下：

(1)

其中，系统状态量具体为：

X=[ΔXc1ΔPg1Δf1ΔPtieΔXc2ΔPg2Δf2]T

(2)

U=[ΔPc1ΔPc2]T

(3)

ΔPL=[ΔPL1ΔPL2]T

(4)

式中：X为状态向量；U为控制向量；ΔPL为扰动向量；A、B、G分别为状态矩阵、控制矩阵、扰动矩阵，且均为定常实矩阵，各矩阵取值由系统内部耦合特性决定。

如果对该系统状态空间添加线性最优反馈环，只能根据扰动进行延时比例调节，如文献[20]中最优控制仅能对区域频率偏差、传输功率偏差进行有差调节，存在局限性。二次调频环应能实现对系统的无差调节，因此，需要对原系统状态空间增加积分器，引入新的状态量。在此引入区域控制误差(area control error,ACE)的积分作为系统新增状态量，该状态量可表达为：

EACi=BiΔfi-ΔPtie

(5)

(6)

式中:i=1,2，分别代表两个区域。

因此，新增积分项后的状态空间表达式为：

(7)

系统状态量为：

(8)

式中：Aa、Ba和Ga的取值详见附录A。

判断该系统状态空间的能控性，系统能控性矩阵为：

(9)

矩阵M满秩，系统能控，新增的ACE积分项不改变闭环最优系统稳定性与可解性。

由于负荷扰动项的存在，无法直接求解该状态空间的全状态最优反馈矩阵，需进行等效变换，化为标准型。

电力系统负荷具有阶跃性，在实际系统中，负荷变化可被视为不断进行短期阶跃的过程，而系统内部状态变化可视作从一个稳态转移到另一个稳态的过程。在此基础上，定义新的扰动变量为：

(10)

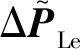
定义新的状态空间为：

(11)

(12)

其中，稳态量ΔXae应为：

(13)

且应有：

ΔXgie=ΔPgie=ΔPLie

(14)

(15)

式中:i=1,2。

因此，近似等效转换后的状态空间应为：

(16)

其中，系统零状态为:

(17)

至此，经过以上等效变换，系统的全状态最优反馈矩阵已可进行求解。

1.3 全状态最优反馈控制的求解

首先，建立动态性能指标泛函为：

(18)

式中：J为性能指标泛函；Q为状态偏差量的权系数矩阵，为半正定实对称方阵；R为控制偏差量的权系数矩阵，为正定实对称方阵。Q和R可以从系统内部状态量与外部控制量综合衡量AGC性能。

令：

(19)

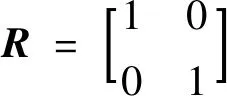
(20)

构建哈密顿函数：

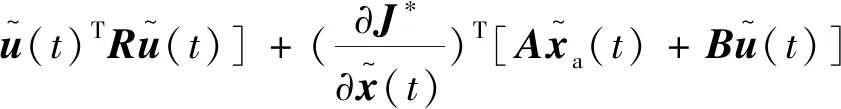
(21)

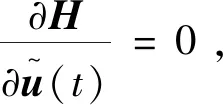
(22)

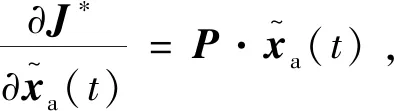
(23)

求解式(24)，可得：

(24)

(25)

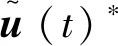
综上，全状态最优反馈矩阵求解完毕。全状态最优反馈下的两区域系统如图2所示，经系统全状态协同反馈，AGC将输出最优发电调控值。

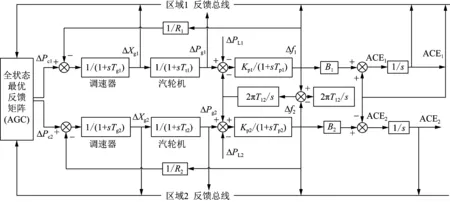
图2 基于全状态最优反馈的两区域互联电力系统负荷-频率控制系统Fig.2 LFC system of Two-area interconnected power system applying FSOF

2 深度置信网络状态最优反馈算法

第1节中建立的FSOF系统存在状态反馈信息过量问题，在实际电力系统中难以实现。因此，本节提出了深度置信网络状态最优反馈算法解决这一问题。

2.1 深度学习与DBN理论基础

深度学习[21]是机器学习的分支，基于深度神经网络(deep neural networks,DNN)实现，通过反向传播(back propagation,BP)算法[22]、对比散度(contrastive divergence,CD)算法[23]等方法对数据样本进行学习，DNN将获取合适的权重与偏置等参数，不断逼近所需表达的自然模型或函数。

本文采用的DNN类型为深度置信网络(deep belief network,DBN)[24]。DBN是由多个受限玻尔兹曼机(restricted boltzmann machine,RBM)堆叠而成的多层神经网络，其模型结构如图3所示。

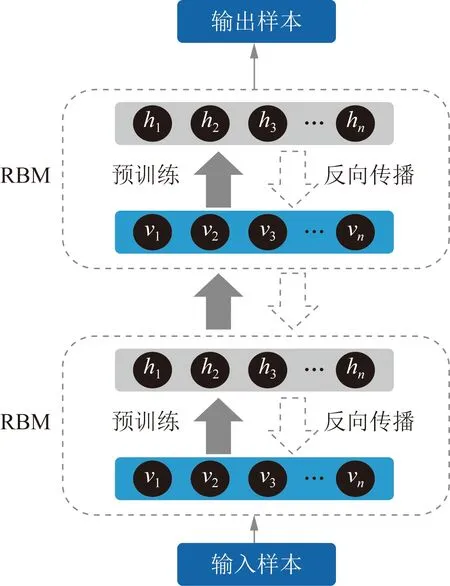
图3 深度置信网络模型Fig.3 Model of deep belief network

与传统BP神经网络不同，DBN是一种基于能量定义的模型，其训练过程是基于能量驱动的。

DBN的能量函数可表示为：

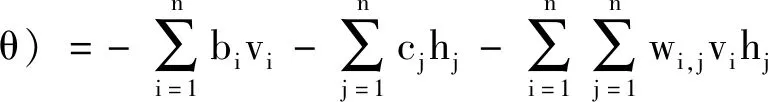
(26)

式中：v是可见神经元的状态向量；h是隐藏神经元的状态向量；vi是第i个可见神经元的状态量；hj是第j个隐藏神经元的状态量；wi,j是连接权重；bi是可见神经元的偏置；cj是隐藏神经元的偏置；θ是所有连接权重和偏置的参数集合。可见，vi和hj的乘积可表示两者之间的相关程度，其与连接权重wi,j一致时，能够得到θ的最大似然估计量。

DBN中神经元的激活是基于概率分布的，(v,h)状态的联合概率分布可表示为：

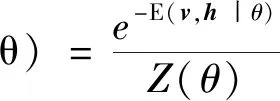
(27)

式中：Z(θ)为归一化函数，其目的是使所有概率分布的总和等于1，可表达为：

Z(θ)=∑v,he-E(v,h 丨θ)

(28)

DBN内各可见神经元及隐藏神经元的激活概率可分别表示为：

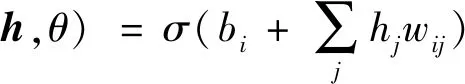
(29)

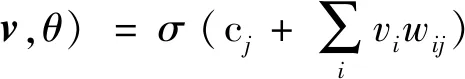
(30)

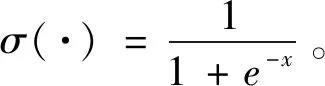
DBN的训练过程可分为以下两个部分：

1)采用CD算法，对各RBM层进行无监督的逐层初始化训练，获取适宜的RBM层内权重及偏置。该部分为DBN的预训练过程，具体实现如下所示。

步骤1：初始化权重、偏置及其他网络参数；

步骤2：令训练样本(输入样本)为vi，根据式(31)计算对应隐层节点的概率，并从这一概率分布中获取隐层节点激活向量样本hj；

步骤3：运算vi和hj的外积，此为“正梯度”；

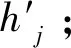
步骤5：运算v′i和h′j的外积，此为“负梯度”；

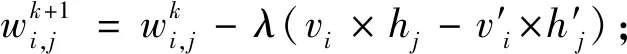
步骤7：判断能量函数是否到达训练目标值，若到达，训练结束；否则重复步骤2—6。

2)首尾相接堆叠各RBM构成DBN，采用误差反向传播算法，对DBN进行有监督的训练，具体实现步骤如下所示。

步骤1：按batch加入训练样本(输入样本与输出样本)；

步骤2：根据输入样本与激活函数σ(·)对神经元进行激活，得到对应的DBN输出值；

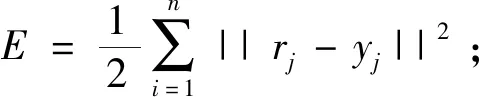
步骤4：根据误差函数的梯度等，修正权重及偏置，如

(梯度下降法)；

步骤5：判断误差函数E是否到达所设定的目标精度，若到达，训练结束；否则重复步骤1—4。

DBN的预训练提升了复杂模型对关键特征的提取能力，一定程度上降低了深度网络的训练难度。完成训练后，DBN已经具备样本特性，可根据输入信息，计算输出符合样本特性的结果。

2.2 深度置信网络状态最优反馈算法

图4阐述了DBNSOF算法及其智能发电控制器(smart generation controller,SGC)的实现过程。

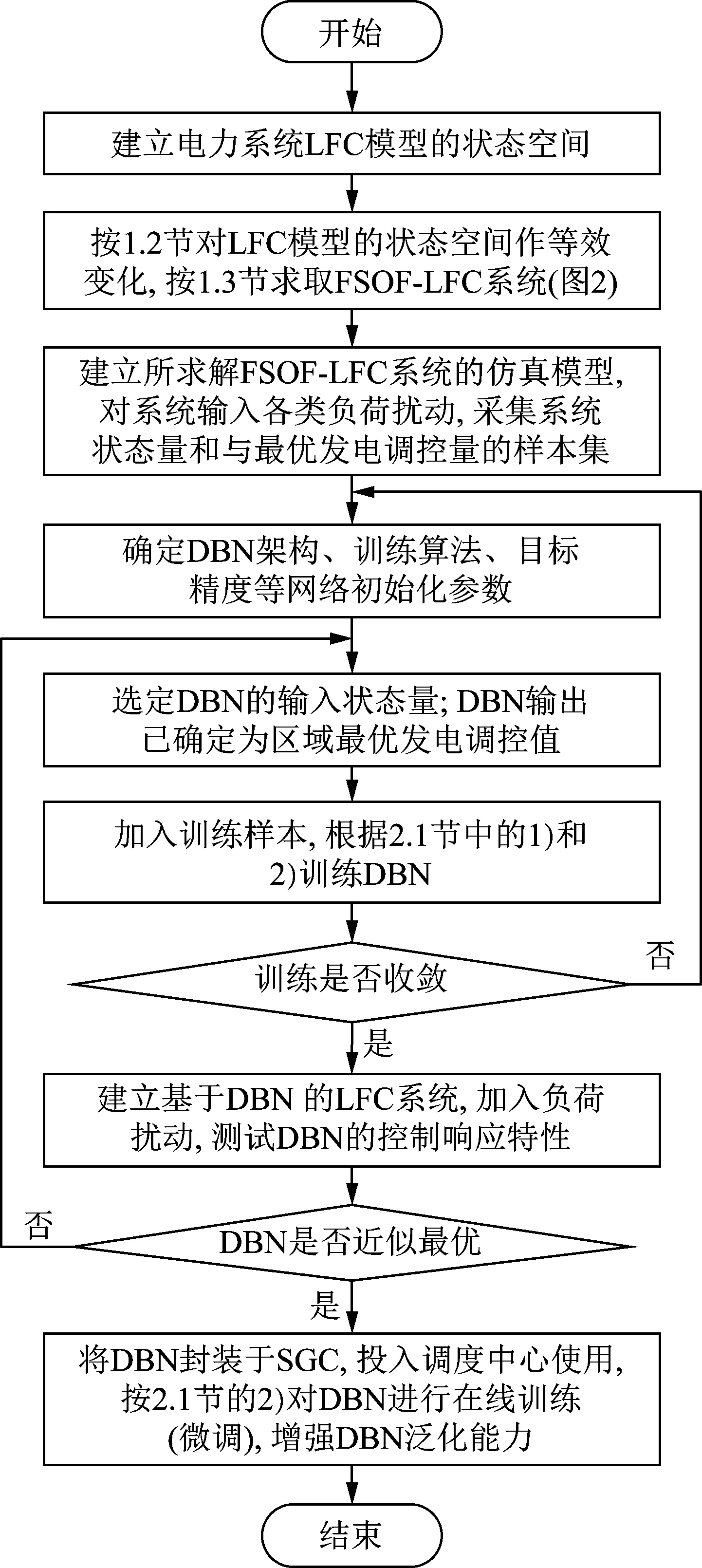
图4 深度置信网络状态最优反馈算法Fig.4 DBN state optimal feedback control algorithm

DBNSOF算法可分为如下2个部分和8个步骤。

1)建立基于全状态最优反馈的负荷-频率控制(FSOF-LFC)系统仿真模型。

步骤1：建立电力系统LFC模型；

步骤2：按1.2节对初始LFC模型的状态空间作等效变化，按1.3节求取FSOF-LFC系统(参见图2)；

步骤3：建立FSOF-LFC系统的仿真模型，对系统输入各类负荷扰动，采集系统状态量和与最优发电调控量的样本集；

2)实现基于DBN的智能发电控制器。

步骤4：确定DBN架构、训练算法、目标精度等网络初始化参数；

步骤5：选定DBN的输入状态量；DBN输出已确定为区域最优发电调控值；

步骤6：加入步骤3中采集的训练样本，根据2.1节中的方法，训练DBN；

步骤7：判断训练是否收敛。若收敛，建立基于DBN 的LFC系统，加入负荷扰动，测试所训练DBN的控制特性指标；否则返回步骤4；

步骤8：判断DBN具备近似最优控制特性，即，DBN是否与全状态最优反馈控制的响应特性具有近似性。若近似最优，将DBN封装于SGC，投入调度中心使用，并根据更新样本集按2.1节的DBN有监督训练算法对DBN进行在线(自适应)训练，对DBN进行微调，增强其泛化能力，否则返回步骤5。

DBNSOF算法中的关键点在于DBN输入状态量的选定，需从两方面权衡考虑：一方面，选定的状态反馈量应与发电调控量有较高的耦合性，以确保DBN训练收敛及其泛化能力；另一方面，选定的状态量应易于测量，并在保证自动发电控制性能的前提下尽可能少，以确保工程中易于实现。此外，需选取适宜的DBN架构与训练算法，以保证训练的收敛性和效率。

2.3 CPS指标

本文将基于控制性能标准(control performance standard,CPS)评价AGC性能，以下对CPS指标进行介绍。

电力系统自动发电控制的目标是使控制区域的频率偏差Δf尽量小，并使各区域间的非计划传输功率ΔPtie也尽量小[25]。因此，为共同衡量Δf、ΔPtie带来的影响，北美电力可靠性委员会(NERC)在1997年提出了统计学性能指标CPS[26]，共同权衡了ACE和Δf带来的影响。ACE和Δf越小，CPS指标越优，自动发电控制性能就越优。CPS具体分为CPS1和CPS2两个指标，如下：

(31)

(32)

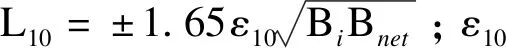
其中，CPS1指标一般取其1min平均值。CPS指标合格充要条件为：满足CPS1>200% 或满足CPS1>100% 且 CPS2>90%。

3 仿真算例

本节通过仿真实验，验证DBNSOF算法的控制性能。仿真实验的硬件环境为CPU型号为i5-7500 3.40 GHz、RAM容量为8 GB的个人工作站；软件环境为MATLAB R2019b。

3.1 基于DBNSOF的智能发电控制器的实现

本节对基于DBNSOF算法的SGC实现过程作具体介绍，如以下步骤所示。

步骤1：此算例以基于IEEE标准两区域系统进行仿真，建立如图1所示的电力系统LFC模型。

步骤2：根据1.2与1.3节求解得全状态最优反馈控制解，所得最优反馈矩阵K0取值详见附录A，FSOF-LFC系统详见图2。

步骤3：在Simulink中建立步骤1中求解的全状态最优反馈控制系统仿真模型(如图2所示)，对系统输入各类负荷扰动，其中包括正弦型扰动、白噪音型扰动、斜坡型扰动等典型扰动，同时对系统中的各状态量和最优发电调控量进行采样。此次采样的仿真时间为107 824 s，实际样本写入时间为213 s。

步骤4：构建由3层RBM堆叠而成的DBN，DBN预训练采用CD算法，BP训练采用基于共轭梯度的BP算法[27]，训练均方误差目标精度设定为9 MW2。

步骤5：DBN输入选定为自区域频率偏差与传输功率偏差及其组合运算值，其中运算方式包括组合基本四则运算、积分运算等，共构成6个输入，DBN输出为区域最优发电调控值;

步骤6：对DBN加入对应类型的训练样本，按2.1节中的方法，训练DBN。其中，预训练(无监督训练)样本来自于步骤3中所采集的区域频率偏差和传输功率偏差；有监督训练样本来自于所采集的区域频率偏差、传输功率偏差和区域最优发电调控值。此次训练中，两区域DBN训练样本均超100万组，训练误差下降过程如图5所示，已收敛至目标精度。理论上，两DBN均应已具备最优发电控制特性。将DBN封装于SGC内，输入区域频率偏差Δf与传输功率偏差ΔPtie，即可输出近似最优发电调控值ΔPao，SGC模型如图6蓝色区域所示。

图5 深度置信网络训练过程Fig.5 DBN training process

步骤7：对所设计的SGC作初步仿真实验，测试其发电控制响应特性。首先在Simulink环境中进行建立LFC仿真模型，如图6所示，模型参数见表1，其中，智能发电控制器通过S-function模块调用训练好的DBN实现。向区域1输入500 MW的阶跃负荷扰动，DBNSOF、FSOF、SO、PI等控制算法下的发电控制响应如图7所示，控制性能指标如表2所示，其中，td是延迟时间，tr是上升时间，ts是调节时间，Mp是超调量，ess是稳态误差(tss=60 s)，上述指标将用于衡量不同控制算法响应的相似程度。根据图表可知，DBNSOF控制与FSOF控制的各控制特性十分相近。

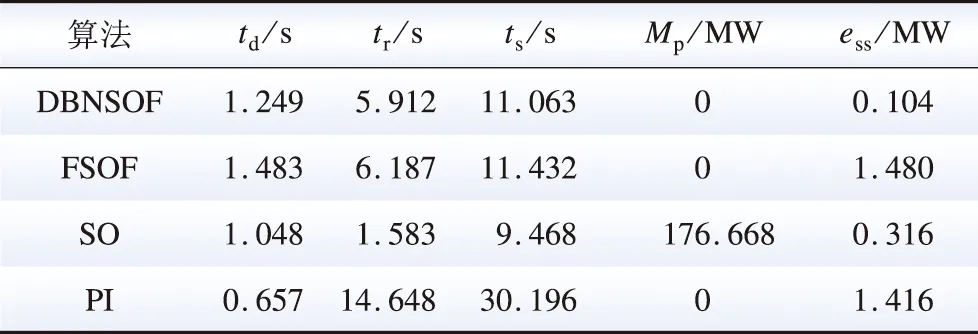
表2 阶跃负荷扰动下的AGC性能指标Table 2 AGC performance index under step load disturbance

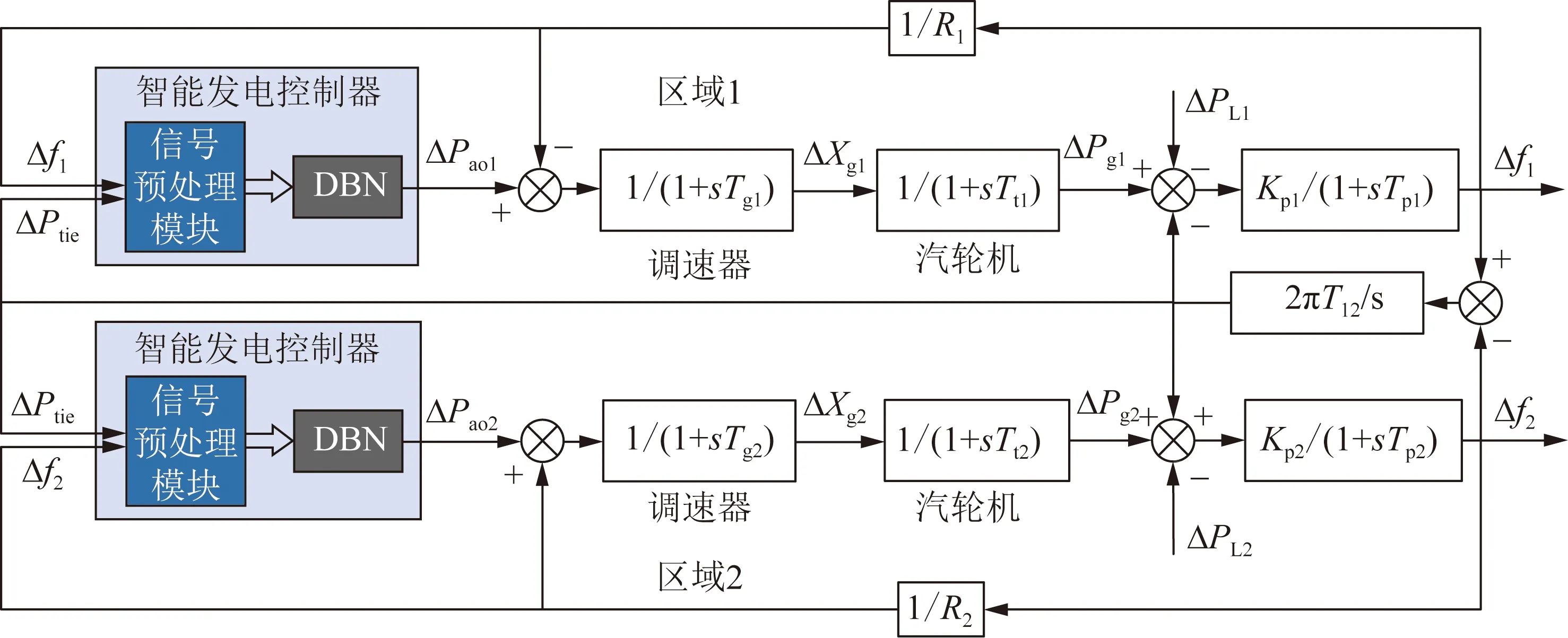
图6 DBNSOF控制下的两区域互联系统负荷-频率控制模型Fig.6 LFC model of two-area interconnected power system under DBNSOF control

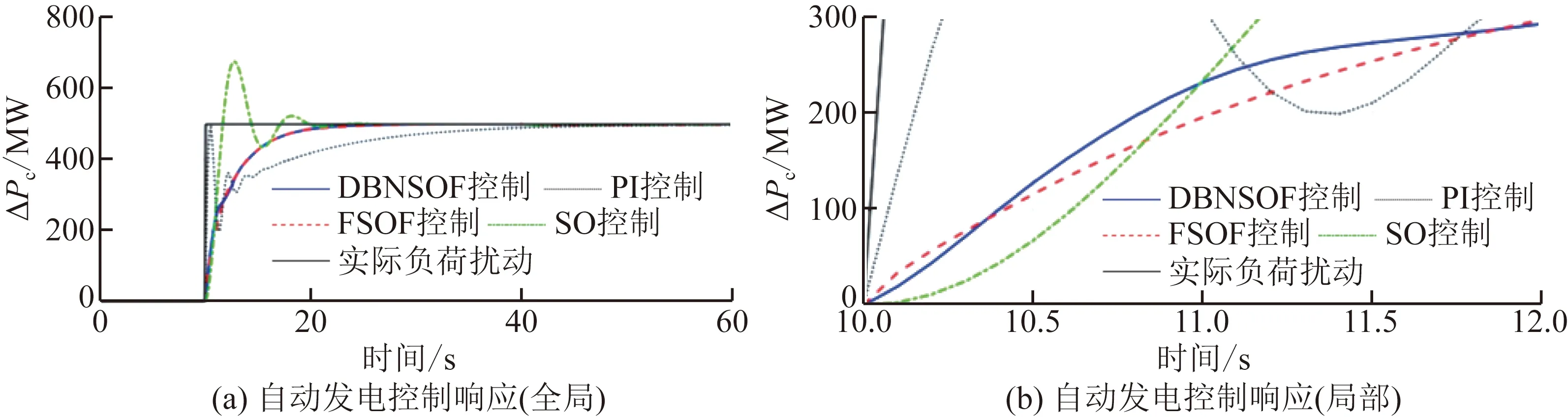
图7 阶跃负荷扰动下的自动发电控制测试Fig.7 Automatic generation control test under step load disturbance

相较之下，SO控制存在振荡，PI控制的响应较慢，均劣于DBNSOF控制与FSOF控制。综上，所训练的DBN是具备近似最优控制特性的，基于DBNSOF算法的SGC已设计完成。本例具有典型性，对于其他电力系统LFC模型的SGC的设计工作，也可参照如上步骤进行。

3.2 仿真运算与分析

为验证DBNSOF算法的近似最优性、稳定性与鲁棒性，在此对3.1节中所实现的SGC作进一步仿真。

考虑实际电力系统是一个典型随机系统，在系统参数和外部负荷扰动上均具有高度随机性，该文将分别基于标称参数IEEE标准两区域系统LFC模型和参数摄动IEEE标准两区域系统LFC模型进行仿真(以下简称“标称参数系统”和“参数摄动系统”)。其中，标称参数系统中各系统参数是固定的，具体值见表1；参数摄动系统中各系统参数在表1的基础上附加幅值为±0.3 pu、采样周期为30 s的白噪音扰动，白噪声扰动是功率谱在整个频域内均匀分布的噪声扰动，理论上可覆盖实际系统中因各类情况产生的参数摄动。对标称参数系统和参数摄动系统输入正弦扰动与白噪音扰动叠加形成的复合负荷扰动，其中，正弦扰动的周期为1 256 s，幅值为1 000 MW，白噪音扰动的幅值为±200 MW，采样周期为10 s。采用4种算法进行仿真运算，AGC仿真结果如图8和图9所示，CPS指标统计结果如表3和表4所示。其中的DBNSOF、FSOF、SO和PI分别代表深度置信网络状态最优反馈、全状态最优反馈、次优和比例-积分控制算法。

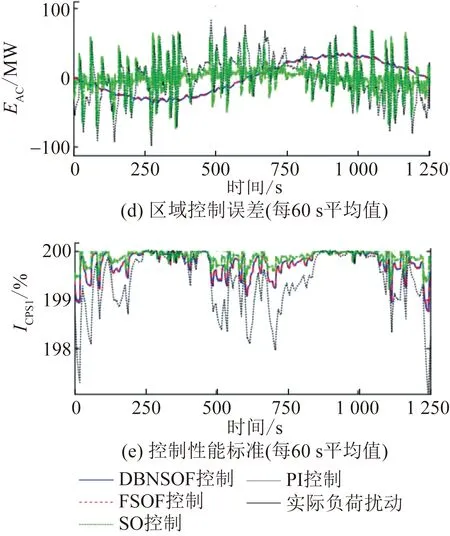
图8 标称参数系统的自动发电控制仿真结果Fig.8 AGC simulation results of nominal parameter system

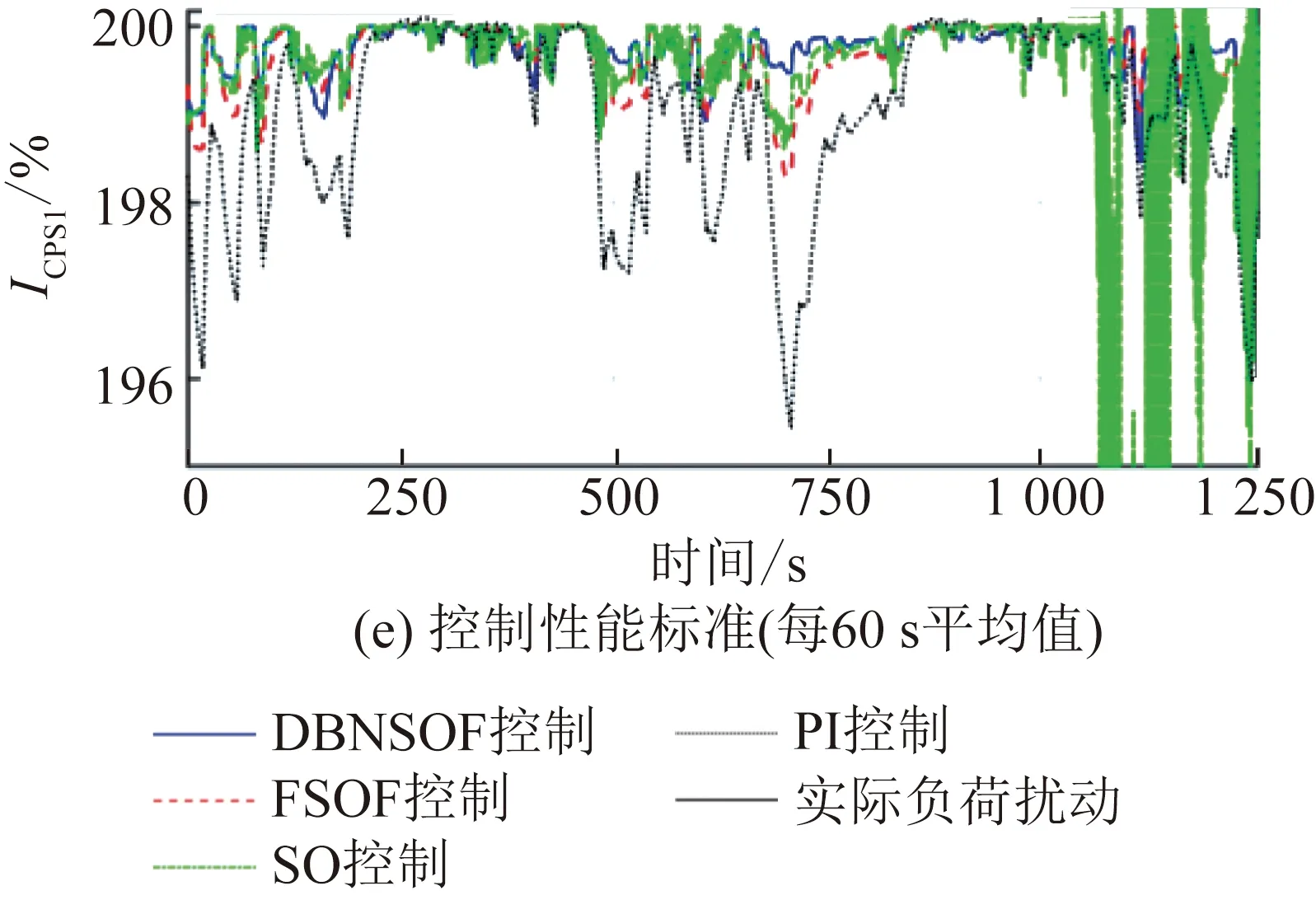
图9 参数摄动系统的自动发电控制仿真结果Fig.9 AGC simulation results of system with uncertain parameters

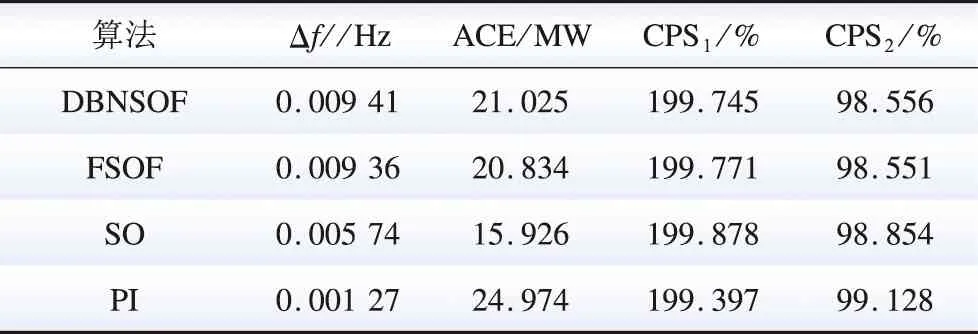
表3 标称参数系统的AGC仿真结果统计表Table 3 AGC simulative statistical results of nominal parameter system

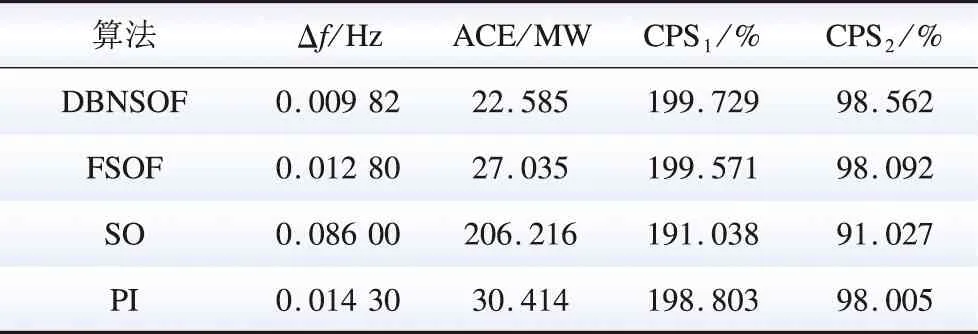
表4 参数摄动系统的AGC仿真结果统计表Table 4 AGC simulative statistical results of system with uncertain parameters

由以上算例分析结果可知，总体上，在上述两次仿真中，DBNSOF的发电控制响应曲线均与负荷扰动曲线高度拟合，响应准确且迅速，仿真时段内的Δf平均值为0.009 82 Hz(取表3和表4中更不利的数据，下同)，ACE平均值为22.585 MW，CPS1的平均值为199.729%，CPS2合格率为98.556%，各项指标在各算法中均为最优。DBNSOF算法在复杂扰动下标称参数系统仿真中的响应特性(图8(b))与图7一致，验证了DBNSOF的稳定性。DBNSOF算法在参数摄动系统仿真结果，对比标称参数系统仿真结果无明显控制性能指标下降(对比表3和表4)，验证了DBNSOF算法的鲁棒性。

以下将DBNSOF算法与其他算法作具体对比分析：

1)对比FSOF控制算法：在标称参数系统中，DBNSOF算法在复杂扰动下的控制曲线仍与FSOF算法十分相似，各性能指标也十分相近(见表3)，进一步验证了DBNSOF所具备的近似最优性。在参数摄动系统中，DBNSOF算法的各性能指标对比标称参数系统时无明显下降，优于具有参数依赖性质的FSOF算法(见表4)。该现象是DBN非线性处理能力和泛化能力的体现。

2)对比SO控制算法：SO的超调和振荡使其能在连续负荷扰动中更早达到下一短期稳态值，因此其在标称参数系统仿真中达到了更好的性能指标(见表3)。然而，振荡系统的鲁棒性一般较差，在某些参数摄动情况下可能面临失稳问题，这在此次仿真中得到体现(见图9(b))，各性能指标急剧下降(见表4)，这一风险是电力系统所不能承受的。此外，SO的振荡性质对调频机组有不利影响。DBNSOF算法在上述问题中均优于SO算法。

3)对比PI控制算法：在标称参数系统中，P系数和I系数整定良好的PI算法与DBNSOF算法的控制性能差距并不十分明显。然而，在某些系统参数摄动下，P分量可能引起振荡(如图9(b)所示)，导致控制性能指标下降(如表4所示)，加大了与DBNSOF算法的差距。因此，DBNSOF算法是优于PI算法的。

综上，基于DBNSOF算法的SGC具备近似最优发电控制特性，其CPS指标在上述算法中最优，并具备更强的鲁棒性。

本文设计的SGC在投入调度中心AGC系统使用后，仍可根据更新的发电调控历史数据进行在线训练和参数更新，SGC的泛化能力、稳定性与鲁棒性也将进一步增强。

4 结 语

本文提出了深度置信网络状态最优反馈算法，利用深度置信网络的非线性表达能力，实现了减少状态反馈量与提升自动发电控制性能的双目标，实现了由自区域频率偏差与传输功率偏差组合反馈下的互联电力系统近似最优发电控制，可以解决全状态最优反馈控制在AGC中的应用难题，符合智能电网建设中对AGC性能的更高要求。同时，DBN的在线学习能力可以适应电力系统产生的实时变化，更适用于系统随机性更强的现代电力网络。

此外，本文所提出的DBNSOF算法并不局限于自动发电控制，对其他控制问题，如自动电压控制，也有借鉴意义，后续将应用此算法进行无功优化等方向的研究。