高比例新能源电网多源最优协同调频策略

何廷一，李胜男，陈亦平，吴水军，沐润志，和鹏，孟贤，何鑫，杨博，曹璞璘

(1.云南电网有限责任公司电力科学研究院，昆明市 650200；2.中国南方电网电力调度控制中心，广州市 510663；3.云南电力试验研究院(集团)有限公司，昆明市 650200；4.昆明理工大学电力工程学院，昆明市 650500)

0 引 言

近年来，为减少对化石燃料的依赖，世界各国致力于发展以风光为代表的新能源。但风电机组、光伏机组的输出在很大程度上受天气的影响，其发电出力存在较大的随机波动，使得发电侧“弃风”、“弃光”等现象常有发生[1-3]。因此，为避免该现象的发生，有必要对其展开研究，使之成为优质的调频资源，缓解传统水火电厂的调频压力，加快系统调频的动态响应性能。

电网调频技术的应用旨在当电网受到负荷变化扰动时，将电网的频率控制在稳定范围内。传统的调频机组主要由水、火电机组来构成，其调节惯性较大，难以快速响应功率输入命令[4]。近年来，随着新能源机组的大规模并网，其输出依靠电力电子设备调节，可以快速响应动态的功率输入调节命令，因此，风电机组、光伏机组可采用定功率点控制方式，将其控制在低于最大功率点的运行工况，留有一定的备用容量参与到二次调频[5]。

目前，二次调频工程领域常根据可调容量来按比例地分配各机组输出功率，该方法称为按比例分配(proportion method,PROP)，但该策略无法满足系统最优控制需求[6]。另外，目前风光新能源参与调频的大部分研究主要关注控制器的设计、风电场及光伏电站自身的控制策略，较少研究风光新能源与其他调频资源之间的协同控制。因此，有必要开发风光电站与传统水火电站之间的最优协同调频方法。文献[7]建立了多源互补控制模型，实现了多源协同互补控制。文献[8]构建了包含风电、光伏及抽水蓄能电站收益的多目标函数，实现了风光新能源与其他调频资源的协同控制。文献[9]建立了二次调频指令最优分配模型，并采用基于改进策略的优化算法求解该模型。但上述文献建模相对简单，未考虑各机组间的动态响应特性。另外，该问题为复杂的非线性优化问题，传统的数学方法具有搜索能力差，难以获得全局最优的缺陷。与之相比，多目标遗传算法(non dominated sorting genetic algorithm-Ⅱ,NSGA-Ⅱ)[10]、基于强度Pareto进化算法2(strength pareto evolutionally algorithm 2,SPEA2)[11]等多目标智能优化算法具有收敛速度快等优点，但全局搜索能力还有待提高。

为此，本文尝试搜索能力更强、收敛速度更快的多目标蝠鲼觅食优化算法(multi-objective manta ray foraging optimization，MMRFO)进行求解，其可以获得分布更加广泛、更加均匀的Pareto前沿，并基于熵权法，设计灰靶决策法客观地选择折中解，可以得到最优经济条件下具有最小功率响应总偏差的功率分配方案。为验证该方法的有效性，本文采用基于扩展的两区域负荷频率控制(load frequency control，LFC)模型进行验证。

1 多源协同互补控制模型

1.1 控制框架

基于扩展的两区域LFC模型的调频框架如图1所示。其中，ΔPT为联络线功率偏差；Δf为实时频率偏差；ΔPout为实际功率调节输出；ΔPD为负荷扰动[12]。另外，电网调频控制技术主要由控制器和功率优化分配2个环节组成，控制器通常采用PID控制方式，将实时频率偏差Δf和联络线功率偏差ΔPT作为输入，输出整个区域电网的实时总调节功率ΔPC，随后由功率分配算法分配ΔPC至各个调频机组。

图1 基于扩展两区域LFC模型的调频框架Fig.1 Framework of frequency regulation on extended two-area LFC model

1.2 约束条件

功率分配过程中，为保证电力系统的稳定运行，须重点考虑功率平衡约束、爬坡约束(generation ramp constraint,GRC)、机组容量约束、能量传递约束[12]。

1)功率平衡约束。

在第k个控制周期内，控制器输出的实时总调节功率应等于所有调频机组接收到的功率调节输入指令之和。

(1)

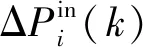
2)机组容量约束。

(2)

(3)

3)GRC和能量传递约束。

表1和图2分别给出了考虑GRC和机组容量约束的不同类型调频机组的动态响应传递函数和动态响应模型。其中，Td为机组二次调频时延；G(s)为机组功率响应传递函数。若不考虑GRC和功率输出限制，实际调节功率输出可通过频域传递函数的拉普拉斯逆变换得到[13]。

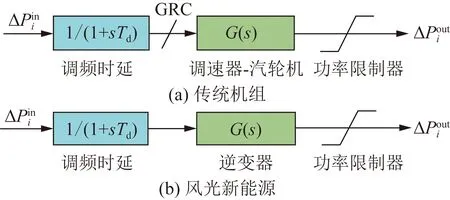
图2 动态响应模型Fig.2 Dynamic response models

表1 不同类型调频机组动态响应传递函数Table 1 Dynamic response transfer functions of different frequency-regulation units

(4)

(5)

(6)

若考虑GRC和功率输出限制，调频机组的输出可改写为：

(7)

(8)

(9)

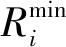
1.3 目标函数

为提升整个区域电网的动态响应性能，设定调节功率指令值和功率响应值的偏差，以及总调频里程支出最小化作为目标函数，可表示为：

(10)

式中：Ri为第i台调频机组的调频里程支出。

(11)

(12)

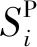
2 多目标蝠鲼觅食优化算法及应用设计

2.1 蝠鲼觅食优化算法

MMRFO受蝠鲼的觅食策略所启发，其中包括链式觅食、螺旋觅食和翻滚觅食。

1)链式觅食。

蝠鲼排成有序的头尾排列，形成一条链来捕捉浮游生物。在MMRFO中，蝠鲼链的目标猎物为浮游生物，因此，假设目前得到的最佳解为浓度较高的浮游生物群。个体根据当前最优解和前一个个体更新当前位置，如下表示[14]：

(13)

(14)

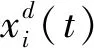
2)螺旋觅食。

当蝠鲼发现深水中有一群浮游生物时，其会采用螺旋的方式进行捕食。在MMRFO中，个体的移动根据前一个个体以及当前最优个体进行更新，该搜索方式可由下式来表示[14]：

(15)

(16)

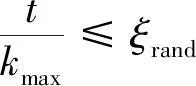
(17)

(18)

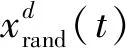
3)翻滚觅食。

在MMRFO中，为提高全局搜索能力，蝠鲼个体会以当前最优解作为支点，进行翻滚操作到与其当前位置成镜像关系的另一侧，如下表示[14]：

(19)

式中：r2、r3为在[0,1]上均匀分布的随机数；S为常数，取值为2。

2.2 Pareto解集存储与筛选

MMRFO会不停更新有限规模的存储池里Pareto解集以完成迭代过程，该过程中，获得的新的非支配解会与存储池里非支配解进行比较，从而判断新的非支配解是否对存储池进行更新，其中分为3种情况[15]：

1)若新的非支配解支配存储池里一个或多个解，则存储池的非支配解将被新的非支配解进行替换；

2)若存储池里至少一个非支配解支配新的非支配解，则不进行更新操作；

3)若存储池里的非支配解与新的非支配解不构成支配与被支配的关系，则将新的非支配解储存在存储池中。

为提升算法的搜索效率，须对存储池的规模进行限制，当非支配解的分布过于密集时，算法将通过下式剔除部分非支配解：

(20)

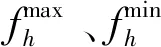
2.3 基于熵权法的灰靶决策法设计

2.3.1效应样本矩阵的设计

基于MMRFO的Pareto解集X为一个n行m列的矩阵，可将X中各解的绝对值作为决策指标之一，亦可作为Pareto前沿的单位解输出，如下表示：

X′(i,j)=|X(i,j)|,i=1,2,…,n,j=1,2,…,m

(21)

为了降低总功率偏差和调频里程支出，2个目标函数值可分别设置为F1和F2。另外，本文引入了一个表示X′中每个解到坐标原点的欧几里德距离的矩阵D，其元素Di如下所示：

(22)

至此，评估指标一共由m+3个构成，即m个Pareto前沿单位解的输出，2个目标函数值以及欧氏距离平方矩阵D。进一步，可将其用矩阵表示为：

X″=[X′F1F2D]

(23)

2.3.2靶心矢量设计

基于奖励最好、惩罚最差原则的算子Zj的计算公式为：

(24)

值得注意的是，所有指标均大于0，且指标越小，代表解的质量更佳，决策矩阵V的元素vij可表示为：

(25)

式中：zij为“奖优罚劣”变换算子；xij为第i个解决方案的第j个目标。

2.3.3靶心设计

本文基于熵权法，设计了灰靶决策法来更客观地选择折中解并得到各个目标函数之间的权重，其中，权重yij和熵值Ej的计算公式为：

(26)

(27)

(28)

(29)

至此，靶心距离最小的解，便可选择为折中解，作为最优的功率分配方案。MMRFO求解流程如图3所示。此外，图4给出了在3个连续的控制周期内，获得的Pareto前沿与被选择的折中解。

图3 MMRFO求解流程Fig.3 Flow chart of MMRFO

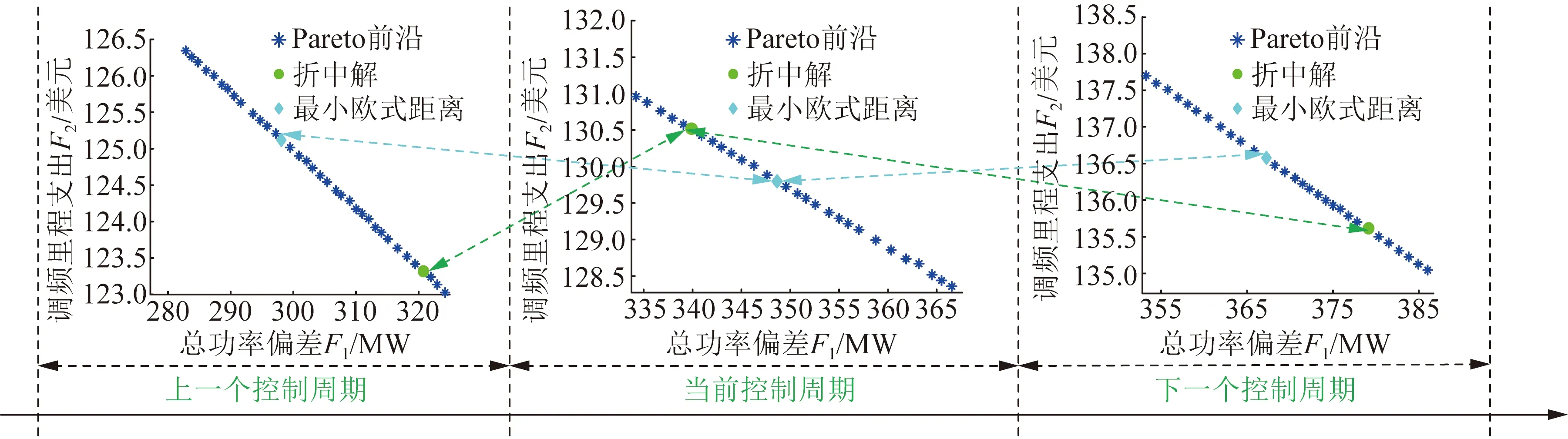
图4 折中解的选择Fig.4 The selection of decision options

3 算例分析

为验证MMRFO以及灰靶决策法的有效性，本文基于扩展的两区域LFC模型进行测试。并引入基于非支配领域选择的多目标免疫算法(multi-objective immune algorithm with non-dominated neighbor-based selection,NNIA)[16]、NSGA-Ⅱ[10]以及SPEA2[11]进行比较。为公平比较各算法的搜索性能，所有算法的种群大小和最大迭代次数均分别设置为N=50和kmax=50。其中，调频控制时间周期为4 s，调频里程价格为2美元/MW。此外，各机组的传递函数参数如表2所示，表3给出了各机组的主要参数。

表2 调频机组的传递函数参数Table 2 Parameters of transfer functions of frequency-regulation units

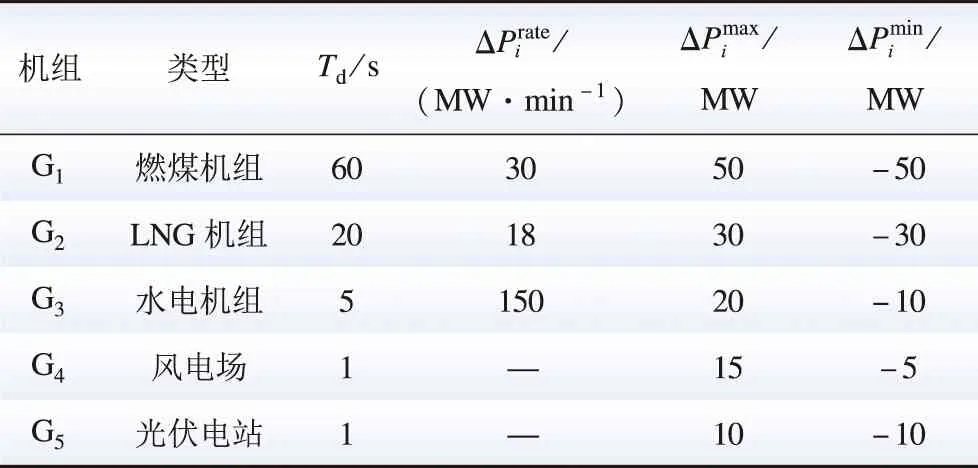
表3 调频机组的功率调节参数Table 3 Main parameters of power regulation of frequency-regulation units

3.1 算法性能测试

为测试算法遭遇负荷扰动时的调节能力，本算例采用ΔPD=50 MW和ΔPD=-50 MW的负荷扰动进行测试。图5(a)比较了各算法在ΔPD=50 MW时获得的Pareto前沿，可以看出，NNIA得到的解明显偏离理想的Pareto前沿。另外，NNIA、NSGA-Ⅱ和SPEA2在ΔPD=-50 MW时获得的Pareto前沿表现不佳，如图5(b)所示。而MMRFO在2种功率扰动下能够获取分布最均匀且广泛的Pareto前沿。

图5 基于扩展的两区域LFC模型，4种算法的Pareto前沿比较Fig.5 Comparison of the Pareto front obtained by four algorithms on the extended two-area LFC model

表4给出了各算法运行10次后，包括反转世代距离(inverted generational distance，IGD)[17]、世代距离(generational distance，DG)[18]、纯粹多样性(pure diversity，PD)[19]、超体积(hyper volume，HV)[20]、分布度指标(diversity metric，DM)[21]、广泛性[21]、间距[22]以及平均运行时间的8种指标的平均值和标准差，从而比较各算法的搜索性能，可以看出：

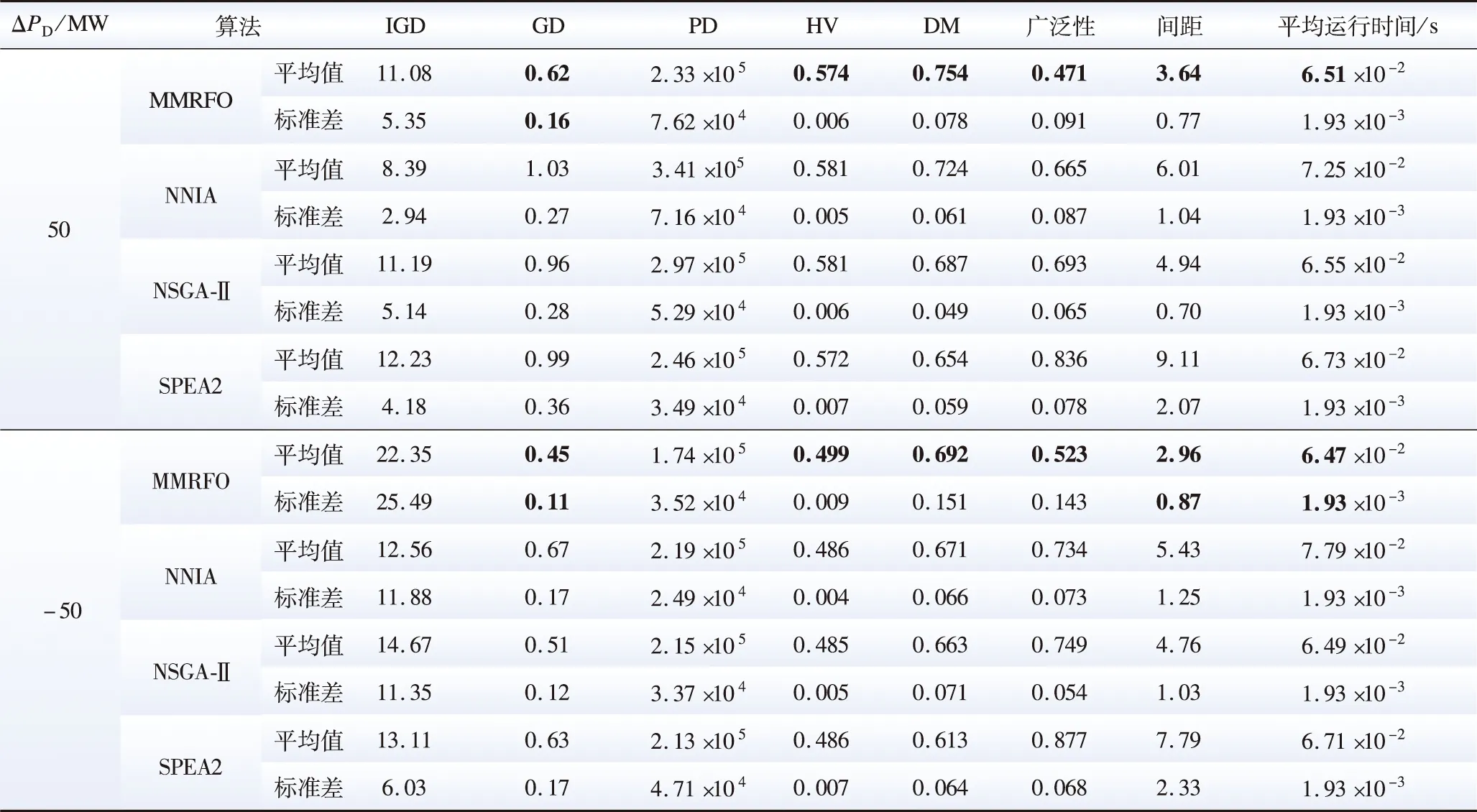
表4 各算法性能比较Table 4 Comparison of performance metrics of algorithms

1)在各算法的IGD、GD平均值中，MMRFO的GD值最小，因此其具有良好的收敛性能；

2)MMRFO的DM和HV平均值明显大于其他算法，PD平均值略小于其他3种算法，证明了其具有表现良好的Pareto前沿多样性；

3)MMRFO具有最小的广泛性、间距平均值，即可证明MMRFO得到的Pareto前沿分布最为均匀且广泛；

4)MMRFO具有最小的平均运行时间，因此其能够最快地收敛到Pareto前沿，从而在最短时间内响应功率调节指令。

3.2 负荷阶跃扰动测试

为进一步验证MMRFO以及灰靶决策法的有效性，本算例采用ΔPD=70 MW和ΔPD=-50 MW的负荷扰动进行测试，并与PROP进行比较[6]。因此，基于PROP，第i台调频机组在第k个控制周期的输出计算公式为：

(30)

ΔPD=70 MW、ΔPD=-50 MW时，基于扩展的两区域LFC模型优化结果分别如图6、7所示。从图6(a)可以看出，MMRFO以及灰靶决策法可以很好地协调各机组之间的功率输出，在ΔPD=70 MW时，获得的总功率偏差显著低于PROP。

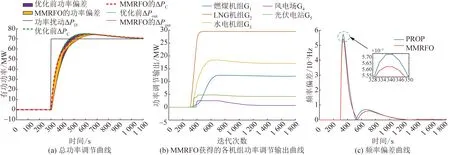
图6 基于扩展的两区域LFC模型优化结果(ΔPD=70 MW)Fig.6 Real-time optimization results obtained on the extended two-area LFC model when ΔPD=70 MW

另外，从图7(a)可以看出，与PROP相比，本文所提方法获得的功率偏差更小，减少了总功率指令的超调，能够在更短时间内恢复受到扰动的系统。

图7 基于扩展的两区域LFC模型优化结果(ΔPD=-50 MW)Fig.7 Real-time optimization results obtained on the extended two-area LFC model when ΔPD=-50 MW

图8给出了不同扰动情况下的调频里程支出变化。综合图6、图7以及图8，可以看出，MMRFO能够在兼顾调频里程支出的前提下，显著提升电能质量。

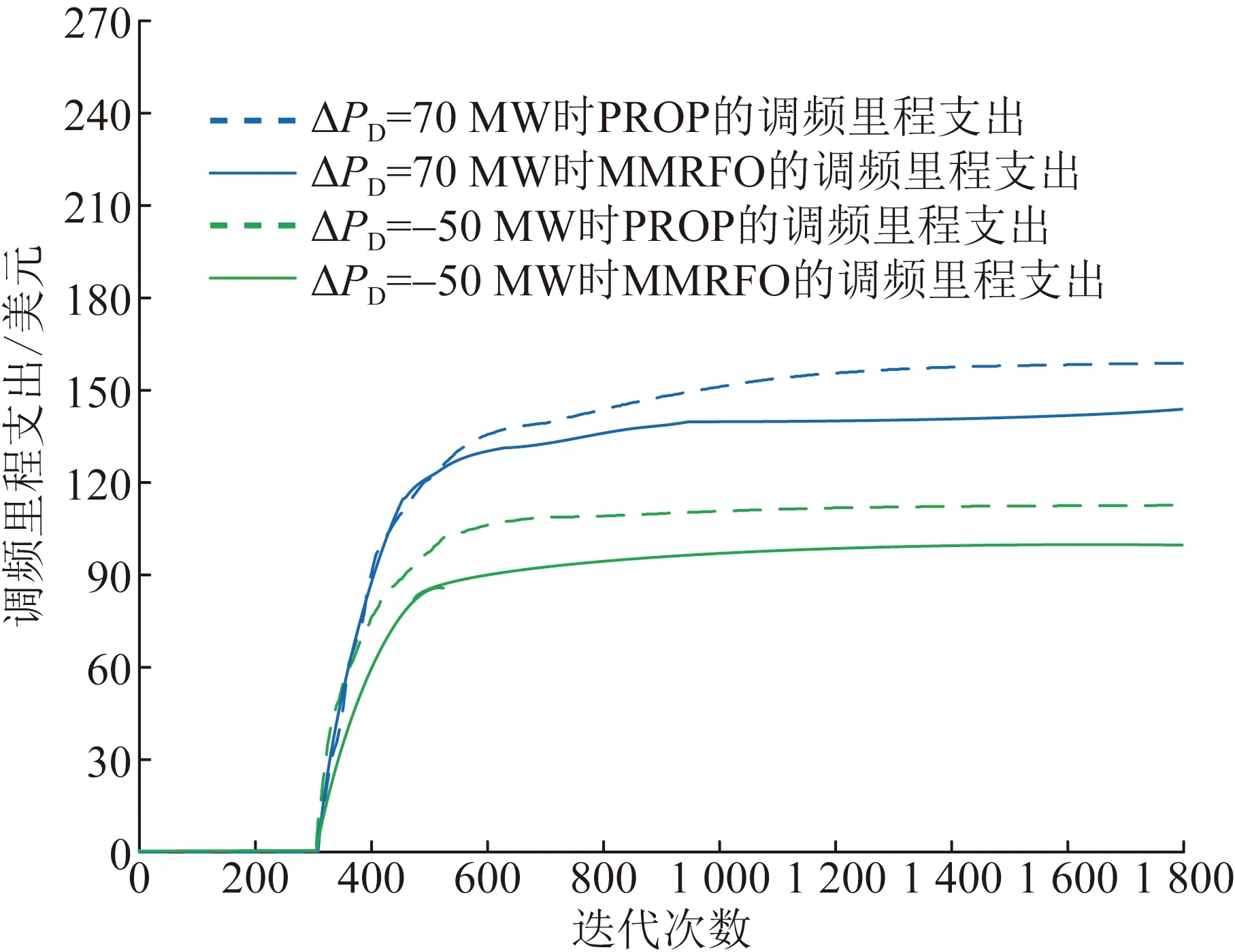
图8 不同功率扰动下的调频里程支出Fig.8 Mileage payment of frequency regulation under four perturbations cases

表5比较了2种工况下的在线优化结果，可知MMRFO方法能够有效减小功率响应总偏差，能够在满足CPS(control performance standard)的前提下降低平均频率偏差|Δf|和区域控制误差绝对值，并有效提升系统的动态响应性能。其中，CPS考核标准包括2个部分,即CPS1和CPS2。CPS1采用基于统计方法来衡量某控制区区域控制误差的变化特性及其与系统频率偏差的关系；CPS2用于评估某控制区域控制联络线潮流偏差的能力。本文采用CPS1对所提方法进行评估。

表5 不同扰动下优化结果比较Table 5 Result comparison of online optimization under different perturbations

4 结 论

本文提出了一种基于多目标蝠鲼觅食优化算法的多源最优协同调频策略，主要贡献为：1)该策略能够在最优经济效益的前提下，有效降低总功率偏差，最优分配各种调频资源；2)多目标蝠鲼觅食优化算法能够在最短时间内获得分布最为均匀且广泛的理想Pareto前沿，而基于熵权法设计的灰靶决策法可以客观地选择折中解，充分发挥各种调频资源的优势；3)针对扩展的两区域负荷频率控制模型进行测试，其结果显示区域控制误差绝对值、平均频率偏差、总功率偏差得到降低，能够在获得最佳经济性的同时提高动态响应性能，证明了该策略能有效地解决多目标优化问题。

为进一步提高经济效益以及系统响应速度，未来将研究装配储能系统的新能源场站，并尝试采用深度强化学习解决该问题，实现多源协同互补控制。