小口径管道自适应内检测机器人研究

毛柳伟，王国庆

（中国人民解放军92578部队，北京100071）

1 引言

作为介质输送的重要方法和途径，小口径管道在船舶、石油化工等领域具有非常广泛的应用。因管道内部长期与流动海水、石油、天然气等各种介质接触，在运行一定时期后，其内部会发生腐蚀、破损、泄漏甚至开裂，严重影响设备的运行安全，给装备的安全服役带来很大的风险隐患［1］。通过一定检测技术手段对管路进行定期检测，及时发现管路缺陷、排除安全隐患，对于保障装备安全运行具有重要意义［2］。因管路外部空间的可达性及技术方法的局限性等，外部检测手段很难全面检测管路内部存在的问题。小口径管道自适应内检测机器人是指可在直径30mm到200mm的管道内自主行走，且通过传感器对管道内部状态进行检测的自动化装置［3-4］。内检测机器人不受外部空间限制，可实现管道内部360度的全覆盖检测，检测能力强，效率高，可全面掌握管道内部缺陷状态。管道内检测机器人的结构主要包括腿式、履带式、轮式等［5-8］。小口径管道内部空间小，转弯半径小，对内检测机器人的变径、转弯等自适应能力要求高［9-10］。针对现有管道机器人在小口径管道中的变径能力、过弯能力不足的问题，设计了一种小口径管道内检测机器人，采用Solidworks及ADAMS软件进行仿真计算，研究了其在管道内的运动特性，为小口径管道的内检测机器人研制提供理论支撑。

2 结构组成及工作原理

管道机器人原理设计，如图1所示。机器人整体由行走机构与变形机构构成。行走机构包括直流电机，锥齿轮，轴，行走轮，外架等。变形机构包括变径架，中间轴，变径座以及弹簧等。

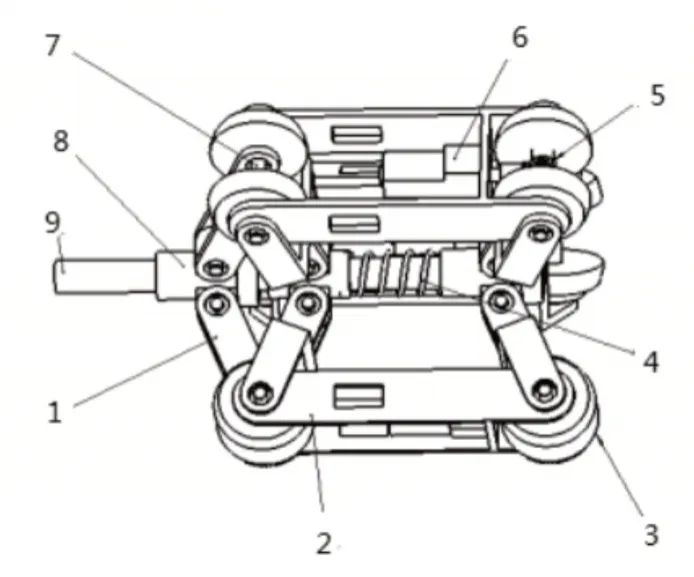
图1 机器人原理设计图Fig.1 Schematic Design of Internal Testing Robot

直流电机通过一对锥齿轮驱动主动轴上的行走轮（前轮）转动，使机器人能够在管道内行进。两个变径座之间安装有弹簧，最初进入管道时，弹簧的预紧力将变径座撑开，使履带轮紧贴管道内壁。当管道内径变大或变小时，弹簧会自动伸长或缩短，来调节两个变径座之间的距离。

3 变径及过弯能力分析

3.1 变径能力分析

机器人运动原理，如图2所示。

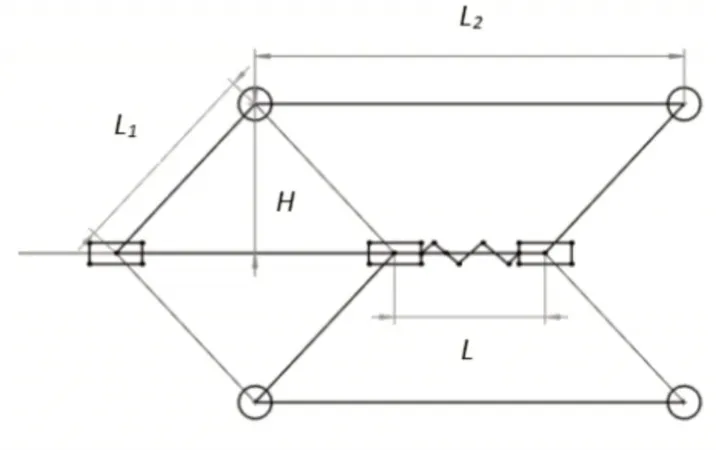
图2 机器人运动原理图Fig.2 Schematic Diagram of Robot Movement

机器人长度约为100mm，搭配不同规格的弹簧将具有不同的变径能力。前后两个变径座中心分别到前后行走轮的距离均为L1为45mm，前后两个轮之间的距离L2为75mm，变径座长为15mm，L为弹簧长度与变径座长度之和，此时从机器人中心到轮中心的距离为H。通过计算可以得出：

轮子的直径d为20mm，所以机器人适应的管子直径为2H+20。所设计的机器人模型适应的管子半径与变径座中心之间的距离L的关系，如图3所示。由图3可见，机器人变径范围与变径座中心之间距离呈线性关系，机器人适应的管径随着变径座之间距离的变大而变大，变径范围约为（95～105）mm之间。

图3 管子半径与变径座中心间距的关系Fig.3 The Relationship Between the Pipe Radius and the Center Distance of Reducer

3.2 转弯能力分析

依据实际工况条件，设定管道弯头角度为90°。机器人在内部行走过程中轮子紧贴管壁，运动状态示意图，如图4所示。

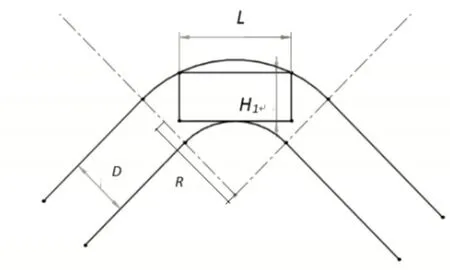
图4 机器人弯道通过能力示意图Fig.4 Schematic Diagram of Robot Turning Ability

机器人适应的最小管径为2H，其在管道弯头中间的部分最难通过，因此能够通过弯头中部就能通过整个管段。能够通过的弯管尺寸应满足［11］：

式中：R-管子弯曲半径；D/2-管道半径。

管道机器人采用的弹簧受压缩后最短长度是10mm，爬行的管道半径为50mm时，可得管道弯曲半径大于200mm，满足公式（2）的弯管通过要求。结果表明设计的机器人可以通过弯曲半径在200mm以上的管子。

4 ADAMS仿真分析

4.1 模型建立

ADAMS在三维建模方面建模类型比较单一，因此选择在SolidWorks环境中建立机器人的零件模型并完成装配，装配完成后，通过接口将样机模型导入到ADAMS中来进行仿真分析。建立机器人仿真模型，如图5所示。

图5 机器人样机模型Fig.5 The Robot Prototype Model

导入完成后，添加约束条件。在ADAMS/View环境下可以添加零件间的所有约束［12］。按实际情况添加约束后，开始仿真计算。

4.2 仿真结果与分析

机器人在管道中行走时，会受到管子对机器人的作用力，并且作用力的大小受到弹簧预紧力的影响，弹簧的预紧力越大则作用力也就越大。摩擦力的存在能使机器人行走的更加平稳，在通过管径变化的部位时不容易发生打滑的现象，但是摩擦力过大也会对电机的牵引力造成负担，因此选择合适的预紧力很有必要。

机器人在给定速度与预紧力5N的情况下在不同管径的直管行走时行走轮受到压力随时间的变化，如图6所示。图中轮子受到的力会出现振动是因为管子与轮面不能充分接触的缘故，由图6可见，管径在105mm时轮子受到的压力为4.4N左右；管径在100mm时轮子受到的压力为5.1N左右；管径在95mm时轮子受到的压力为5.8N左右；可以看出轮子与管壁的接触力随着管径变小而增大。

图6 在给定速度与预紧力下行走轮受到的压力Fig.6 The Pressure on the Walking Wheel at a Given Speed and Preload

在给定速度下，在管径100mm的直管中，机器人行走轮在不同预紧力下受到的压力随时间变，如图7所示。由图可见，预紧力为5N时轮子受到的压力为5N左右；预紧力为6N时轮子受到的压力为6.1N左右；预紧力为7N时轮子受到的压力为6.9N左右；由结果可知，轮子与管壁的作用力随着预紧力的增大而逐渐增大。图中轮子受到的力会出现振动是因为管子与轮面不能充分接触的缘故。

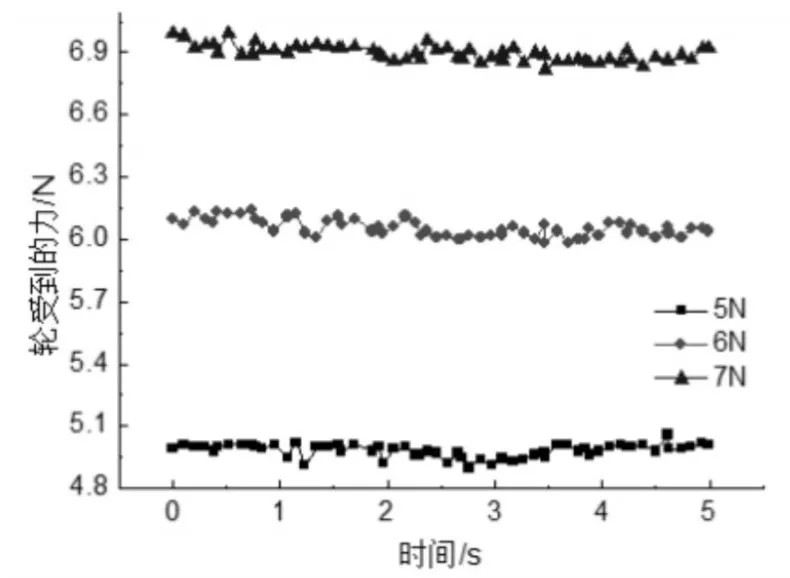
图7 不同预紧力下行走轮受到的压力Fig.7 The Pressure on the Walking Wheel at Different Preload

在给定速度下，机器人由直径105mm的管爬行至直径95mm的管道时，行走轮在不同预紧力下受到的压力，如图8所示。由图可见，当弹簧预紧力5N时，行走轮受到压力约6N，摩擦系数约0.3，需要提供的扭矩约为0.18NM，当弹簧预紧力为6N时，行走轮受到的平均圧力约为7N，需要提供的扭矩约为0.22NM，设计的机器人选用电机扭矩为0.4NM，取安全系数为1.5，因此预紧力在6N以下的弹簧满足电机的要求。当预紧力为7N时，可以看出轮子受到的力出现波动，这是因为预紧力过大电机不能驱动机器人通过95mm的管，行进到中途便退回原来的105mm管，在电机驱动下继续前进然后再退出来，因此7N预紧力不能满足电机的要求。考虑到摩擦力会使机器人运动平稳因此选择预紧力为6N的弹簧。图中轮子受到的力会出现振动是因为管子与轮面不能充分接触，可以看出在经过一段时间后轮子受到的力有一个明显的提升，这是因为结果表明弹簧被压缩，提供的力也变大，因此轮子受到的力也变大。弹簧预紧力确定时，通过理论计算可以校核电机驱动力能否满足需要。

图8 不同预紧力下通过变径时行走轮受到的压力Fig.8 The Pressure on the Walking Wheel through Reducing at Different Preload

在给定速度、预紧力为6N的情况下，机器人通过直径为105mm的弯管（管子弯曲角度为90°，弯曲半径为200mm）时，行走轮受到压力随时间变化，如图9所示。由图可见，机器人具有弯曲半径为200mm的管道的通过能力。图中曲线出现较大波动是因为机器人通过管道弯曲部位，轮子受到的力比在直管中受到的力更大所导致。

图9 转弯时行走轮所受压力变化图Fig.9 The Pressure on the Walking Wheel through Pipeline Elbow

在预紧力为6N，电机扭矩为0.4NM的情况下，机器人由直径105mm的管爬到了直径95mm的管，然后通过直径105mm的弯管（管道弯头角度90°，转弯半径200mm），在此过程中，机器人的速度变化，如图10所示。由结果可见，机器人速度先增加后降低然后又增加然后又降低。这是因为机器人首先在105mm的管子中行走，受到的阻力较小，速度升高，然后进入到95mm的管子中，阻力变大，速度降低，然后进入105mm弯管，弯管头部阻力小速度升高，进入弯曲部分后，机器人受管道压迫加剧，速度降低，通过弯曲部分后，压迫变小，速度升高。结果表明，驱动力矩为0.4NM时，机器人可以顺利通过同时包含变径及弯管的管道。

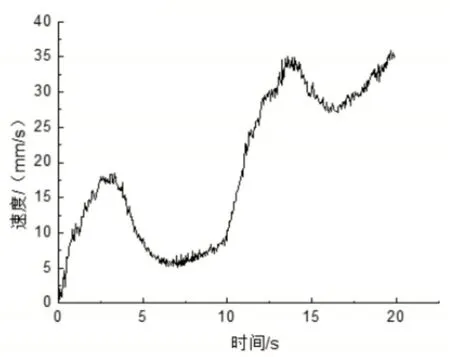
图10 机器人在含变径及弯头的管道内速度变化Fig.10 Robot Speed Change in Pipeline with Reducing and Elbow

5 结论

理论计算结合SolidWorks与ADAMS仿真实现对小口径管道内检测机器人的设计及运动能力分析。小口径管道内检测机器人变径范围与变径座中心之间距离呈线性关系，机器人适应的管径随着变径座之间距离的变大而变大，变径范围约为95mm-106mm。机器人弹簧最短长度在10mm以下、预紧力为6N时，可顺利通过弯曲半径在200mm以上的管道。仿真分析数据及计算结果，可作为小口径管道内检测机器人物理样机设计、研制的理论依据，同时为同类机器人研究提供借鉴和参考。